Numerical calculation of hydrodynamic characteristics of tidal currents for submarine excavation engineering in coastal area

Jian-hua Li,Liang-sheng Zhu*,Shan-ju Zhang

College of Civil and Transportation Engineering，South China University of Technology，Guangzhou 510640，China

Received 30 December 2015；accepted 1 April 2016

Available online 25 June 2016



Numerical calculation of hydrodynamic characteristics of tidal currents for submarine excavation engineering in coastal area

Jian-hua Li,Liang-sheng Zhu*,Shan-ju Zhang

College of Civil and Transportation Engineering，South China University of Technology，Guangzhou 510640，China

Received 30 December 2015；accepted 1 April 2016

Available online 25 June 2016

Abstract

In coastal areas with complicated flow movement,deposition and scour readily occur in submarine excavation projects.In this study,a smallscale model,with a high resolution in the vertical direction,was used to simulate the tidal current around a submarine excavation project.The finite volume method was used to solve Navier-Stokes equations and the Reynolds stress transport equation,and the entire process of the tidal current was simulated with unstructured meshes,generated in the irregular shape area,and structured meshes,generated in other water areas. The meshes near the bottom and free surface were densified with a minimum layer thickness of 0.05 m.The volume of fluid method was used to track the free surface,the volume fraction of cells on the upstream boundary was obtained from the volume fraction of adjacent cells,and that on the downstream boundary was determined by the water level process.The numerical results agree with the observed data,and some conclusions can be drawn:after the foundation trench excavation,the flow velocity decreases quite a bit through the foundation trench,with reverse flow occurring on the lee slope in the foundation trench；the swirling flow impedes inflow,leading to the occurrence of dammed water above the foundation trench；the turbulent motion is stronger during ebbing than in other tidal stages,the range with the maximum value of turbulent viscosity,occurring on the south side of the foundation trench at maximum ebbing,is greater than those in other tidal stages in a tidal cycle,and the maximum value of Reynolds shear stress occurs on the south side of the foundation trench at maximum ebbing in a tidal cycle.The numerical calculation method shows a strong performance in simulation of the hydrodynamic characteristics of tidal currents in the foundation trench,providing a basis for submarine engineering construction in coastal areas.

©2016 Hohai University.Production and hosting by Elsevier B.V.This is an open access article under the CC BY-NC-ND license(http:// creativecommons.org/licenses/by-nc-nd/4.0/).

Small-scale model；Tidal current；Hydrodynamic characteristic；Coastal area；Submarine excavation engineering；Reynolds stress model

1.Introduction

Submarine excavation projects should be constructed precisely when they involve complicated construction conditions, such as channel excavation engineering,submarine pipeline engineering,and submarine immersed tube tunnel engineering.Back silting and slope damage usually occur in excavation projects,owing to deposition and scour.This problem has crucial implications for engineering construction.For example,the 15th immersed tube of the Hong Kong-Zhuhai-Macau Bridge could not be placed in the foundation trench due to serious sedimentation(Li,2015).When immersed tubes were sunk and installed,the lateral force,drifting force,and mooring force acting on the tubes changed significantly because of the hydrodynamic change(Lu et al.,2014). Therefore,investigation of the hydrodynamic characteristics for submarine excavation projects in coastal areas is highly significant.

Tidal action is one of the most important impact factors in a coastal area.The horizontal scale of a tidal current is much greater than its vertical scale.Based on the static pressure hypothesis,three-dimensional shallow water equations havebeen derived using the water level variable instead of the pressure variable(Liu and He,2000).According to previous studies,three-dimensional large-scale hydrodynamic models, such as the Princeton ocean model(POM)(Ohashi and Sheng, 2013；Gao et al.,2013),the environmental fluid dynamics code model(EFDCM)(Zhou et al.,2014；Ren et al.,2015),the estuarine,coastal,and ocean model(ECOM)(Ningsih and Azhar,2013),the coupled hydrodynamical ecological model for regional and shelf seas(COHERENS)(Shi et al.,2010；Tuomi et al.,2012),and the finite-volume coastal ocean model(FVCOM)(Chen et al.,2007),have been commonly used to study the spatial and temporal variability of tidal current movement.Their commonly used turbulence submodels are the Smagorinsky,the Mellor and Yamada,and the k-ε models(Abbott,1997).The sigma coordinate mode along the vertical direction has also been used to fit both the free surface and bed topography(Berntsen and Furnes,2005).

The large-scale hydrodynamic models mentioned above have been limited to two-dimensional or weakly threedimensional flows over a large calculation range,meaning that they are only meshed at a low resolution in the vertical direction,considering the effect of computational efficiency.If the terrain changes drastically,the sigma coordinate mode cannot achieve a high resolution in both shallow and deep waters(Gr¨awe et al.,2015；Berntsen et al.,2015).It is also difficult to densify the local water area in the vertical direction (Tao and Zhang,2007).Therefore,a small-scale model should be used to study the tidal current in a study region around submarine excavation projects.

Small-scale models have been used to solve the Navier-Stokes equations and analyze flow structures in complicated calculation domains(Tang et al.,2015).They have the advantages of smaller grids,more layers,and higher resolutions in the vertical direction(Tang et al.,2014).Using the smallscale model in the simulation,the characteristics of unidirectional flow around the submarine structures were focused on, and the currents at the upstream boundary were considered the inflow to the calculation domains(Wu and Wang,2009；Lubin et al.,2010；Nielsen et al.,2013).However,the results could not reflect the entire process of reciprocating motion due to tidal currents,even though the hydrodynamic characteristics during ebbing and flooding were also studied.Lefebvre et al. (2014)investigated the dynamic behavior of the bedforminfluenced flow field and roughness lengths over a large bedform during a tidal cycle by establishment of a small-scale model with more than 50 layers in the vertical direction. However,their study essentially simulated unidirectional flow in ebbing and flooding,respectively,and the hydrodynamic characteristics for transition were not studied.

In this study,we aimed at obtaining the hydrodynamic characteristics of tidal currents for submarine excavation projects.The finite volume method was used to solve the Navier-Stokes equations and the Reynolds stress transport equation.With the foundation trench excavation in the Hong Kong-Zhuhai-Macau Bridge Project in the Pearl River Estuary as an example,the processes of tidal movement after the foundation trench excavation were simulated,and the numerical results were compared with the observed data for the purposes of analyzing the reasonability of the numerical calculation method used in this study.

2.Mathematic model descriptions

2.1.Governing equations

The basic governing equations for mass and momentum conservation(Pope,2000；Zhao et al.,2013)are as follows:

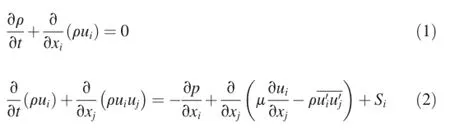
where uiand ujare the velocity components in the xiand xjdirections,respectively,and i,j=1,2,3；p is the pressure；is the Reynolds stress；t is time；ρ is the density of fluid；μ is the dynamic viscosity coefficient；and Siis the momentum source term.

Considering anisotropics of turbulent viscosity,the Reynolds stress model(Versteeg and Malalasekera,2007)was used in this study.The Reynolds stress transport equation and turbulent dissipation rate transport equation(Pope,2000；Duan et al.,2015)are shown below:

where the subscript r means the xrdirection；DT,ijis the turbulent diffusion term；DL,ijis the molecular diffusion term；Pijis the stress production term；Gijis the buoyancy production term；φijis the pressure strain term；εijis the dissipation term；Fijis the production term according to the system rotation；k is the turbulent kinetic energy；ε is the turbulent dissipation rate；μtis the turbulent viscosity；SRSand Sεare the source terms；σεis the Prandtl number for ε with a value of 1.3；and Cε1,Cε2, and Cε3are constants with the values of 1.44,1.92,and 0, respectively.DL,ij,Pij,and Fijonly contain two-order correlation terms,and DT,ij,Gij,φij,and εijcontain uncertain correlation terms,which can be calculated as follows:

where σkis the Prandtl number for k with a value of 1.0,δijis the Kronecker function,nmis the component of the unit normal vector in the xmdirection,and d is the distance to the wall.The values ofandare 1.8,0.6,0.5,and 0.3,respectively；and,where κ is the von K■arm■an constant with a value of 0.4187,and Cμ=0.09.

The air-water interface was considered in this study,and the volume of fluid(VOF)method was used to track the free surface in the model(Rui et al.,2015).In a cell,Fwand Faare the volume fractions of the water phase and air phase, respectively,and 0≤Fw(or Fa)≤1.They are in the relation as follows:

2.2.Calculation of hydrodynamic characteristics

Drastic turbulence takes place in the vicinity of submarine projects.The hydrodynamic characteristics can be analyzed by calculating the characteristic parameters (Launderand Spalding,1974),including the turbulent kinetic energy k,the turbulent viscosity μt,the Reynolds shear stresses τxy,τxz,and τyz,and the wall shear stress τw,as follows:

where uWA,kWA,and dWAare the mean velocity,the turbulent kinetic energy,and the distance from the wall adjacent cell to the wall,and E is an empirical constant with a value of 9.793.

2.3.Numerical calculation scheme

2.3.1.Numerical solution method

The finite volume method was used to solve Reynoldsaveraged Navier-Stokes equations,combined with the Reynolds stress model(Pope,2000).Considering the characteristics of tidal currents and computational efficiency,the pressure-implicit with splitting of operators(PISO)algorithm was used to calculate the pressure and velocity(Jang et al.,1986).The PISO algorithm is based on the higher degree of the approximate relation between the corrections for pressure and velocity.It can maintain a stable calculation with a larger time step for both momentum and pressure(Issa, 1986).

The discretization schemes for the diffusion term and the convection term were carried out using a central difference scheme and a second-order wind scheme,respectively.The discretization schemes for the turbulent kinetic energy,turbulent dissipation rate,and Reynolds stress were implemented using a first-order upwind scheme.The numerical oscillation was limited because the upwind scheme could maintain the stability of numerical calculation.The stability condition (Courant et al.,1967)in the calculation process is as follows:

where CFL is the Courant number,V is the cell volume,Aiis the area of cell face i,and λimaxis the maximum of local eigenvalues.

2.3.2.Mesh generation

With the foundation trench excavation in the Hong Kong-Zhuhai-Macau Bridge Project in the Pearl River Estuary as an example,hybrid meshes were generated in the calculation domain.The mesh in the vertical direction was densified at a high resolution in a local region.Unstructured meshes were generated to fit the irregular shape of the structural sections and drastic terrain.Structured meshes were generated in other water areas and at the wall boundary.The meshes near the bottom and free surface were densified.

Fig.1 and Fig.2(a)present the calculation domains and meshes before and after the foundation trench excavation.The wedge element was used for the area of the foundation trench, and the hexahedral element was used for the other parts.Along the vertical direction,the meshes near the bottom and free surface were densified with a minimum layer thickness of 0.05 m.According to the observed hydrologic data,there is a mainly reciprocating current in the area between the outlets of the Lingding Estuary and Lantau Island.Therefore,the x direction of the calculation domain was set along the north-tosouth direction.The width of the foundation trench with its baseline perpendicular to the flow direction was 50 m.A composite slope was set on both sides with lower segment and upper segment gradients of 1:3 and 1:7,respectively(Cao and Xiao,2012).Its bottom elevation was-45 m,and the bottom width along the flow direction was 42 m.The size and meshesof the foundation trench after excavation can be seen in Fig.2(b).

Fig.1.Schematic diagram of calculation domain and mesh generation before foundation trench excavation(units:m).

2.3.3.Boundary conditions

The varying processes of velocity and water level were set astheupstream and downstream boundary conditions, respectively.The x direction of the domain was set to be along the dominant flow direction,so the lateral boundaries along the x direction were set as symmetry boundaries.The other boundaries were set as wall boundaries.

The time series of the velocity and water level data were obtained from the simulated results of the tidal currents in the Pearl River Estuary using a large-scale model.On the water level boundary,the pressure is in accordance with the assumption of static pressure distribution.It can be calculated with

where Psis the absolute pressure on the water level boundary, Pais the standard atmospheric pressure,g is the gravitational acceleration,η is the position of the free surface,and z is the vertical coordinate value.

The volume fractions of cells on the upstream boundary were obtained from adjacent cells at the previous time step. For the water phase,the volume fraction for surface cell i on the upstream boundary is as follows:

where t′is the time step,andis the volume fraction of the water phase of the adjacent cell at the previous time step. FwU（i,0）can be determined by the initial flow field.

The volume fractions of cells on the downstream boundary were obtained based on the water level process.For the water phase,if(x0,y0,z0)is the centroid of the free surface on the downstream boundary,the volume fraction for surface cell i on the downstream boundary is determined as follows:

where ziis the vertical coordinate of the centroid of cell i,hwlis the water level at the current time step,and Δz is the grid spacing in the z direction.

3.Application of numerical calculation method

3.1.Validation

In this study,the precision of the numerical calculation method was validated with the observed data at an observation station in the Lingdingyang Estuary under natural conditions. The observed data were obtained by one-day observation (from 12:00 on August 6 to 12:00 on August 7,2008)using an acoustic wave and current meter.The corresponding monitoring point was set at the center of the calculation domain, located at(505,-22.5).

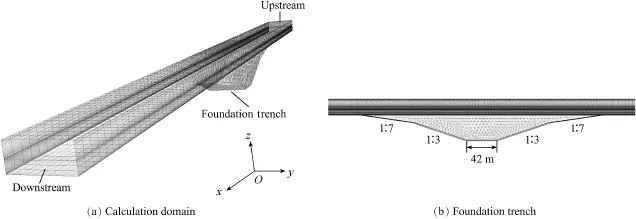
Fig.2.Schematic diagrams of calculation domain and mesh generation after foundation trench excavation.

3.1.1.Validation of water level

The water level process calculated at the monitoring point matches the observed values,as shown in Fig.3(a).The relative error is less than 0.4%.For the numerical results,the highest water level is 11.90 m and the lowest is 10.20 m, which are the same as the observed values.During flooding and ebbing,the calculated values are slightly higher than the observed values,indicating that the water level process obtained from the numerical simulation is reasonable.

3.1.2.Validation of depth-averaged velocity

The time series of the calculated results of the depthaveraged velocity atthe monitoring pointmatch the observed values,as shown in Fig.3(b).The calculated and observed results have the same period,and their maximum and minimum values appear at the same time.The average values of the calculated and observed results of the depthaveraged velocity during flooding(from 20:00 on August 6 to 01:00 on August 7)are 0.35 m/s and 0.39 m/s,respectively, with a relative error of 10.26%.The average values of calculated and observed results of the depth-average velocity during ebbing(from 01:00 to 07:00 on August 7)are 0.44 m/s and 0.51 m/s,respectively,with a relative error of 13.73%.At maximum flooding(at 00:00 on August 7),the calculated and observed values are 0.51 m/s and 0.55 m/s,respectively,with a relative error of 7.27%.At maximum ebbing(at 06:00 on August 7),the calculated and observed values are 0.63 m/s and 0.71 m/s,respectively,with a relative error of 11.27%. Fig.3(b)shows that the calculated results are slightly lower than the observed values.The error is caused by the discharge boundary data obtained from the calculated results of the Pearl River Estuary with the large-scale tidal current model.

3.1.3.Validation of vertical distribution of flow velocity

Fig.4 shows the vertical distributions of flow velocity(u)at the monitoring point at different times during flooding and ebbing.Figs.4(a)through(d)show the velocity distributions during flooding,and Figs.4(e)through(h)show the velocity distributions during ebbing.In the simulation,the changes in temperature and salinity were not considered.The distributions follow the logarithmic law(Ni et al.,2009),and the calculated results show errors as compared with the observed values,which are caused by the stratification and mixing phenomena.At 22:00 and 23:00 on August 6 and 02:00 and 03:00 on August 7,the distributions match the observed data, and the stratification is weak.However,when the stratification strengthens,the deviations between the calculated results and observed data grow.Moreover,the deviations during ebbing are relatively small.

3.2.Engineering application

3.2.1.Hydrodynamic characteristics under natural conditions

Fig.3.Comparisons of calculated and observed values of water level and depth-averaged velocity at monitoring point.

During a tidal cycle,the duration of ebbing is longer than that of flooding,and the water level rises slowly during flooding and drops rapidly during ebbing.Fig.3 shows that the time of the maximum value of water level lags behind that of the maximum value of flow velocity during a tidal cycle. During flooding,the calculated maximum value of flow velocity is 0.51 m/s,occurring before the high tide level.In the initial stage of flooding,the flow velocity continues to decrease and reaches 0 after 21:00 on August 6.This is due to land runoff and the inertial force of ebbing.Then,it reverses and beginsto increase.During ebbing,thecalculated maximum value of flow velocity is 0.63 m/s,occurring before the low tide level.In the initial stage of ebbing,the flow velocity continues to decrease and reaches 0 after 01:00 on August 7.Then,it reverses and begins to increase.The transition of flow velocity of tidal currents in the lower layer precedes that in the upper layer(Fig.5),due to the inertia of water particle movement(Xie et al.,2011).In general,the flow velocity in the upper layer is larger than that in the lower layer. It is easier for water particles to overcome the inertia in the lower layer than in the upper layer.Therefore,it is easier for flow to reverse its direction in the lower layer.

3.2.2.Hydrodynamic characteristics after foundation trench excavation

After the foundation trench excavation,the area of flow section increases,and the flow slows down through the foundation trench.Fig.6 presents the velocity distributions in the section of y=-22.5 m.The vertical distributions of flow velocity show wedge-shaped distributions above the lee slope. The velocities at the monitoring point decrease by 60%and 52%at maximum flooding and maximum ebbing after excavation,respectively,in contrast to those before excavation.

Fig.4.Calculated results and observed values of vertical distributions of flow velocity at monitoring point.

Fig.5.Vertical distributions of flow velocity at monitoring point during transition.

Fig.6.Velocity distributions in section of y=-22.5 m at maximum flooding and maximum ebbing.

Fig.7 presents the flow fields in the section of y=-22.5 m in the foundation trench,with Figs.7(a)through(f)showing the flow fields during flooding,and Figs.7(g)through(l) showing the flow fields during ebbing.It indicates that at 22:00 on August 6 and 02:00 on August 7,the flow slows down without swirling flow occurring during the transition.Then, swirling flow occurs due to the increasing velocity after the transition.Furthermore,reverse flow mainly occurs on the lee slope.When the reverse flow moves upward along the lee slope,dammed water occurs above the foundation trench.The maximum change of water level is 0.036 m according to the water level difference before and after excavation.It can be concluded from Fig.8 that the excavation has little influence on the water level.The results of flow fields match the results of Cao and Xiao(2012),which were obtained based on a twodimensional horizontal numerical model and field tests.

Intense turbulence takes place in the foundation trench due to the occurrence of swirling flow.According to Eqs.(10)through(13),the hydrodynamic characteristics were obtained.The maximum turbulent viscosities at maximum flooding and maximum ebbing are 100 kg/(m·s) after foundation trench excavation,while the corresponding values under natural conditions are 13.6 kg/(m·s)and 55.8 kg/(m·s),respectively,indicating that the excavation of the foundation trench intensifies the turbulence in this area.The comparison ofturbulentcharacteristicsin different tidal stages shows that the turbulent flow is stronger during ebbing than in other tidal stages.As shown in Fig.9,the range with the maximum value of turbulent viscosity,occurring on the south side of the foundation trench at maximum ebbing,is greater than those in other tidal stages in a tidal cycle,and the strong turbulent motion mainly takes place in the water above the stoss slope. However,the turbulent viscosity decreases during the transition,as shown in Figs.9(c)and(d).

Fig.10 shows that the values of Reynolds shear stress τxzat maximum flooding and maximum ebbing are larger than those during the transition,and the maximum value of τxzoccurs on the south side of the foundation trench at maximum ebbing in a tidal cycle,demonstrating that there exists intensiveexchange of water mass in different layers,and the shear velocity shows a large degree of variation due to the occurrence of eddies.

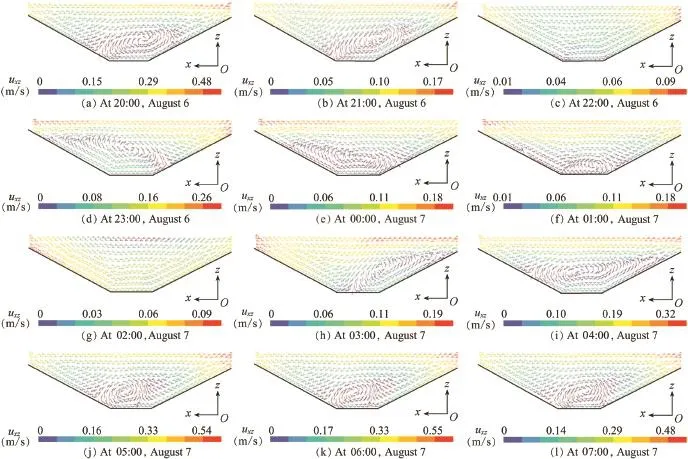
Fig.7.Flow fields in section of y=-22.5 m in foundation trench.

Fig.8.Variations in water level before and after excavation.

Fig.11 presents the wall shear stress distribution along the flow direction at maximum flooding,maximum ebbing,and the transition.The values of wall shear stress at maximum ebbing are largest due to the larger values of flow velocity. During the transition,the values of wall shear stress are small. Furthermore,the wall shear stress is higher on the north side, implying that the frictional resistance is larger on the north side,and the sediment incipient motion and transport occur more readily on the south side.The results match the phenomenon of the thickness of deposition on the north side being greater than that on the south side.Also,the hydrodynamic characteristics obtained in this study agree with a previous study by Xin et al.(2012),in which the hydrodynamic characteristics were obtained based on trial tunnel experiments over a long-period observation.

4.Conclusions

Based on the Navier-Stokes equations and the Reynolds stress model,a three-dimensional small-scale numerical model of tidal currents for submarine excavation projects was established.The results match the observed data and show a strong performance of the numerical model in the simulationof the hydrodynamic characteristics of tidal currents.The following conclusions are drawn:

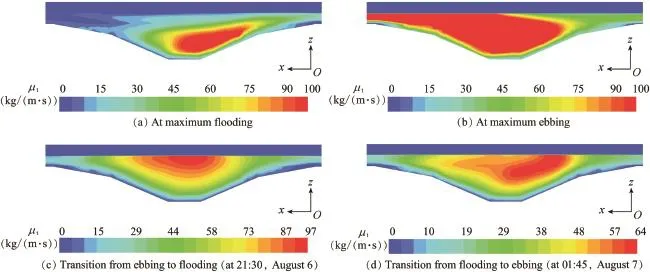
Fig.9.Distributions of turbulent viscosity μtat maximum flooding,maximum ebbing,and transition in section of y=-22.5 m.

Fig.10.Distributions of Reynolds shear stress τxzat maximum flooding,maximum ebbing,and transition in section of y=-22.5 m.

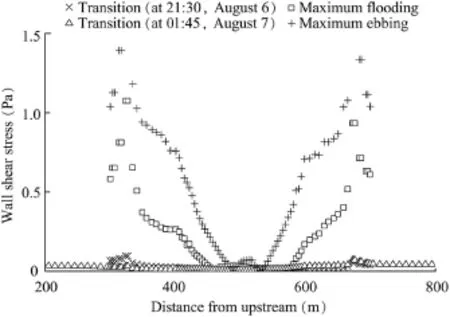
Fig.11.Wall shear stress distribution along flow direction at maximum flooding,maximum ebbing,and transition.

(1)After the foundation trench excavation,the flow velocity decreases quite a bit through the foundation trench,and the reverse flow occurs on the lee slope in the foundation trench.With the action of swirling flow,the reverse flow moves upward along the lee slope,and the inflow is impeded, leading to the occurrence of dammed water above the foundation trench.However,the excavation has little influence on the water level.

(2)The turbulent motion is stronger during ebbing than in other tidal stages.The range with the maximum value of turbulent viscosity,occurring on the south side of the foundation trench at maximum ebbing,is greater than those in other tidal stages in a tidal cycle,and the maximum value of Reynolds shear stress occurs on the south side of the foundation trench at maximum ebbing in a tidal cycle.The hydrodynamic characteristics obtained in this study demonstrate the phenomenon of the thickness of deposition on the north side being greater than that on the south side.The flow field characteristics and hydrodynamic characteristics of tidal currents around the submarine excavation project are reasonably described by the numerical calculation method.

References

Abbott,M.B.,1997.Range of tidal flow modeling.J.Hydraulic Eng.123(4), 257-277.http://dx.doi.org/10.1061/(ASCE)0733-9429(1997)123:4(257).

Berntsen,J.,Furnes,G.,2005.Internal pressure errors in sigma-coordinate ocean models:Sensitivity of the growth of the flow to the time stepping method and possible non-hydrostatic effects.Cont.Shelf Res.25(7-8), 829-848.http://dx.doi.org/10.1016/j.csr.2004.09.025.

Berntsen,J.,Thiem,Ø.,Avlesen,H.,2015.Internal pressure gradient errors in σ-coordinate ocean models in high resolution fjord studies.Ocean.Model. 92,42-55.http://dx.doi.org/10.1016/j.ocemod.2015.05.009.

Cao,H.J.,Xiao,L.B.,2012.Back silting of trench excavation for the immersed tunnel in Hong Kong-Zhuhai-Macao Bridge construction.Port Waterw. Eng.(1),12-17(in Chinese).

Chen,C.S.,Huang,H.S.,Beardsley,R.C.,Liu,H.D.,Xu,Q.C.,Cowles,G., 2007.A finite volume numerical approach for coastal ocean circulation studies:Comparisons with finite difference models.J.Geophys.Res. 112(C03018),1-34.http://dx.doi.org/10.1029/2006JC003485.

Courant,R.,Friedrichs,K.,Lewy,H.,1967.On the partial difference equations of mathematical physics.IBM J.Res.Dev.11(2),215-234.http:// dx.doi.org/10.1147/rd.112.0215.

Duan,D.H.,Zhang,J.B.,Gao,Z.X.,2015.Investigation on spanwise wall oscillation in turbulent channel flow based on Reynolds stress model (RSM). Procedia Eng. 99,665-670. http://dx.doi.org/10.1016/ j.proeng.2014.12.587.

Gao,J.S.,Xue,H.J.,Chai,F.,Shi,M.C.,2013.Modeling the circulation in the gulf of Tonkin,South China Sea.Ocean.Dyn.63(8),979-993.http:// dx.doi.org/10.1007/s10236-013-0636-y.

Gr¨awe,U.,Holtermann,P.,Klingbeil,K.,Burchard,H.,2015.Advantages of vertically adaptive coordinates in numerical models of stratified shelf seas. Ocean.Model.92,56-68.http://dx.doi.org/10.1016/j.ocemod.2015.05.008.

Issa,R.I.,1986.Solution of implicitly discretized fluid flow equations by operator splitting.J.Comput.Phys.62,40-65.http://dx.doi.org/10.1016/ 0021-9991(86)90099-9.

Jang,D.S.,Jetli,R.,Acharya,S.,1986.Comparison of the PISO,SIMPLER, and SIMPLEC algorithms for the treatment of the pressure-velocity coupling in steady flow problems.Numer.Heat.Transf.10(3),209-228. http://dx.doi.org/10.1080/10407798608552506.

Launder,B.E.,Spalding,D.B.,1974.The numerical computation of turbulent flows.Comput.Methods Appl.Mech.Eng.3(2),269-289.http:// dx.doi.org/10.1016/0045-7825(74)90029-2.

Lefebvre,A.,Paarlberg,A.J.,Ernstsen,V.B.,Winter,C.,2014.Flow separation and roughness lengths over large bedforms in a tidal environment:A numerical investigation.Cont.Shelf Res.91,57-69.http://dx.doi.org/ 10.1016/j.csr.2014.09.001.

Li,Z.L.,2015.Three times installation of 15th immersed tube in Hong Kong-Zhuhai-Macau submarine tunnel engineering in Lingdingyang Bay.Constr. Archit.19,13-15(in Chinese).

Liu,H.,He,Y.S.,2000.Recent development in 3-D hydrodynamic mathematical model studies for estuaries.Ocean Eng.18(2),87-93(in Chinese).

Lu,W.Q.,Wu,W.G.,Su,L.W.,Chen,K.Q.,Peng,S.,2014.Hydrodynamic experimental study on immersed tube tunnel element of Hong Kong-Zhuhai-Macao Bridge.China Civ.Eng.J.47(3),138-144(in Chinese).

Lubin,P.,Glockner,S.,Chanson,H.,2010.Numerical simulation of a weak breaking tidal bore.Mech.Res.Commun.37(1),119-121.http:// dx.doi.org/10.1016/j.mechrescom.2009.09.008.

Ni,Z.H.,Song,Z.Y.,Wu,L.C.,2009.Study on the double-logarithmic profile of tidal flow velocity in the near-bed layers.Acta Oceanol.Sin.28(6), 84-92.

Nielsen,A.W.,Liu,X.F.,Sumer,B.M.,Fredsøe,J.,2013.Flow and bed shear stresses in scour protections around a pile in a current.Coast.Eng.72, 20-38.http://dx.doi.org/10.1016/j.coastaleng.2012.09.001.

Ningsih,N.S.,Azhar,M.A.,2013.Modelling of hydrodynamic circulation in Benoa Bay,Bali.J.Mar.Sci.Technol.18(2),203-212.http://dx.doi.org/ 10.1007/s00773-012-0195-9.

Ohashi,K.,Sheng,J.Y.,2013.Influence of St.Lawrence River discharge on the circulation and hydrography in Canadian Atlantic waters.Cont.Shelf Res.58,32-49.http://dx.doi.org/10.1016/j.csr.2013.03.005.

Pope,S.B.,2000.Turbulent Flow.Cambridge University Press,Cambridge, pp.83-95.

Ren,L.,Nash,S.,Hartnett,M.,2015.Observation and modeling of tide-and wind-induced surface currents in Galway Bay.Water Sci.Eng.8(4), 345-352.http://dx.doi.org/10.1016/j.wse.2015.12.001.

Rui,B.F.,Falc~ao,D.S.,Oliveira,V.B.,Pinto,A.M.F.R.,2015.Numerical simulations of two-phase flow in proton exchange membrane fuel cells using the volume of fluid method:A review.J.Power Sources 277, 329-342.http://dx.doi.org/10.1016/j.jpowsour.2014.11.124.

Shi,J.Z.,Li,C.,Dou,X.P.,2010.Three-dimensional modeling of tidal circulation within the north and south passages of the partially-mixed Changjiang River Estuary,China.J.Hydrodynamics,Ser.B 22(5), 656-661.http://dx.doi.org/10.1016/S1001-6058(10)60010-8.

Tang,G.Q.,Chen,C.Q.,Zhao,M.,Lu,L.,2015.Numerical simulation of flow past twin near-wall circular cylinders in tandem arrangement at low Reynolds number.Water Sci.Eng.8(4),315-325.http://dx.doi.org/ 10.1016/j.wse.2015.06.002.

Tang,H.S.,Qu,K.,Wu,X.G.,2014.An overset grid method for integration of fully 3D fluid dynamics and geophysics fluid dynamics models to simulate multiphysics coastal ocean flows.J.Comput.Phys.273,548-571.http:// dx.doi.org/10.1016/j.jcp.2014.05.010.

Tao,J.F.,Zhang,C.K.,2007.Review on several vertical coordinate modes of 3-D flow numerical model in estuarine and coastal waters.Ocean Eng. 25(1),133-142(in Chinese).

Tuomi,L.,Kai,M.,Lehmann,A.,2012.The performance of the parameterisations of vertical turbulence in the 3D modelling of hydrodynamics in the Baltic Sea.Cont.Shelf Res.50-51,64-79.http://dx.doi.org/10.1016/ j.csr.2012.08.007.

Versteeg,H.K.,Malalasekera,W.,2007.An Introduction to Computational Fluid Dynamics:The Finite Volume Method,second ed.Pearson Education Limited,Harlow.

Wu,Z.C.,Wang,D.Z.,2009.Numerical solution for tidal flow in opening channelusing combined MacCormack-finite analysis method.J. Hydrodynamics,Ser.B 21(4),505-511.http://dx.doi.org/10.1016/S1001-6058(08)60177-8.

Xie,D.F.,Pan,C.H.,Wu,X.G.,2011.Three-dimensional numerical modeling of tidal bore in Qiantang based on FVCOM.Ocean Eng.29(1),47-52(in Chinese).

Xin,W.J.,Jia,Y.S.,He,J.,2012.Back silting analysis of the trial dredgedtrough for immersed tube tunnel of Hong Kong-Zhuhai-Macao Bridge. Hydro-Science Eng.(2),71-78(in Chinese).

Zhao,Y.P.,Bi,C.W.,Dong,G.H.,Gui,F.K.,Cui,Y.,Guan,C.T.,Xu,T.J., 2013.Numerical simulation of the flow around fishing plane nets using the porous media model.Ocean.Eng.62,25-37.http://dx.doi.org/10.1016/ j.oceaneng.2013.01.009.

Zhou,J.T.,Falconer,R.A.,Lin,B.L.,2014.Refinements to the EFDC model for predicting the hydro-environmental impacts of a barrage across the Severn Estuary.Renew.Energy 62,490-505.http://dx.doi.org/10.1016/ j.renene.2013.08.012.

This work was supported by the National Natural Science Foundation of China(Grant No.41406005).

*Corresponding author.

E-mail address:lshzhu@scut.edu.cn(Liang-sheng Zhu).

Peer review under responsibility of Hohai University.

http://dx.doi.org/10.1016/j.wse.2016.06.005

1674-2370/© 2016 Hohai University.Production and hosting by Elsevier B.V.This is an open access article under the CC BY-NC-ND license(http:// creativecommons.org/licenses/by-nc-nd/4.0/).