参数方程应用探析

◇　山东　刘淑霞

(作者单位：山东省栖霞市第一中学)



参数方程应用探析

◇山东刘淑霞

参数方程是曲线的另一种表现形式,它弥补了普通方程表示曲线的不足,使得对曲线的研究更加灵活,进一步拓宽了解决问题的思路.下面就对此进行系统梳理,希望帮助同学们查漏补缺、温故知新.

1　常用曲线的参数方程

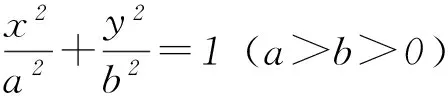
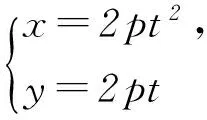
注意:参数方程转化为直角坐标方程时,消去参数方程中的参数即可,但要注意直角坐标方程中变量x、y的取值范围应与参数方程中参数的取值对应,消去参数的具体方法要根据参数方程的特点来考虑.

直角坐标方程化为参数方程,要恰当地选择参数t和函数x=f(t),并且使x=f(t)的值域与直角坐标方程中变量x的范围一致,然后将x=f(t)代人直角坐标方程中解出y=g(t),即得参数方程.

2　曲线参数方程的应用

2.1利用参数方程求距离

直线的参数方程中参数t的几何意义与距离有关,适宜求弦长或距离.

2.2利用参数方程求轨迹

求2条动曲线交点的轨迹方程,常选出一个适当的参数,求出2条动曲线方程或动点坐标适合的含参数等式,再消参,即得所求动点轨迹方程.

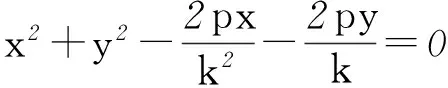
①

x2+y2-2pk2x+2pky=0.

②

因为P(x,y)是异于O点的2圆交点,所以x≠0,y≠0,由式①-②并化简得

y=(k-1/k)x.

③

由式①+②并化简得

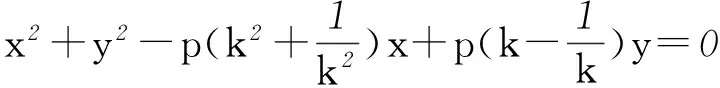
④

由式③得k-1/k=y/x.

⑤

⑥

将式⑤、⑥代入④得x2+y2-2px=0 (x≠0).故点P的轨迹为以(p,0)为圆心,p为半径的圆(除去原点).

2.3利用参数方程研究最值

圆与椭圆的参数方程能够很轻松地利用角表示出圆与椭圆上的点,因此凡是与圆、椭圆上的动点有关的最值问题都可用参数方程解决.

(1) 写出曲线C的参数方程、直线l的普通方程;

(2) 过曲线C上任一点P作与l夹角为30°的直线,交l于点A,求|PA|的最大值与最小值.

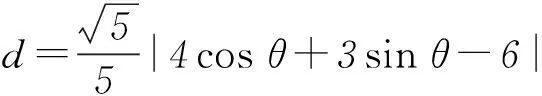
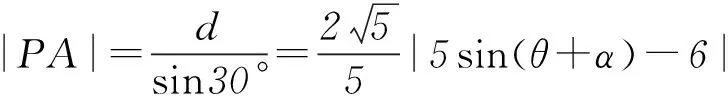
其中α为锐角,且tanα=4/3.

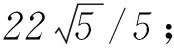
总之,涉及到直线、圆、椭圆、双曲线的部分试题,若用其参数方程来解决,在化归、转换等环节会带来极大的方便,使得运算过程流畅,从而提高解题速度.

(作者单位：山东省栖霞市第一中学)