纯电感线圈路端电压与电流的相位关系

彭建荣，罗凌霄

（大理大学工程学院，云南大理　671003）

纯电感线圈路端电压与电流的相位关系

彭建荣，罗凌霄

（大理大学工程学院，云南大理671003）

通过两种途径严格证明了纯电感线圈的电流与路端电压的相位关系，并给出纯电感线圈的便于操作的定义。

纯电感线圈；电流；路端电压；相位关系

［DOI］10. 3969 / j. issn. 2096-2266. 2016. 06. 007

流过纯电感线圈的电流的相位比其路端电压的相位落后π/2这一结论，电磁学中普遍是在给定电流是余弦函数的前提下推出的〔1〕。有些人可能意识到了这个前提来得有些突然，因而他们换之以电感线圈的路端电压是余弦函数为前提来推导，可惜过程中存在牵强的地方〔2-3〕。实际上，在他们的前提下要推出流过纯电感线圈的电流也为余弦函数这个他们希望得出的结论是不可能的。正因为如此，人们才普遍地避免从路端电压是余弦函数这个前提出发。

作者认为，无论首先给定流过电感线圈的电流为余弦函数，还是首先给定电感线圈的路端电压为余弦函数，都是不妥当的，这是因为，这样的前提条件是否能够实现，是需要用电磁学基本原理论证的。我们所能肯定的是，电源电动势可以是余弦函数。

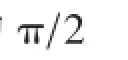
1　与简谐电源联接的电感线圈的详细分析

如图1所示，电源电动势eba=e0cos（ωt+φ0），电源的内阻为r，电感线圈的电感为L，电阻为R。假设构成电感线圈的金属材料和周围的磁性材料是线性的，那么其电感不随电流的变化而改变。电键原先是断开的；t=0时刻，合上电键。

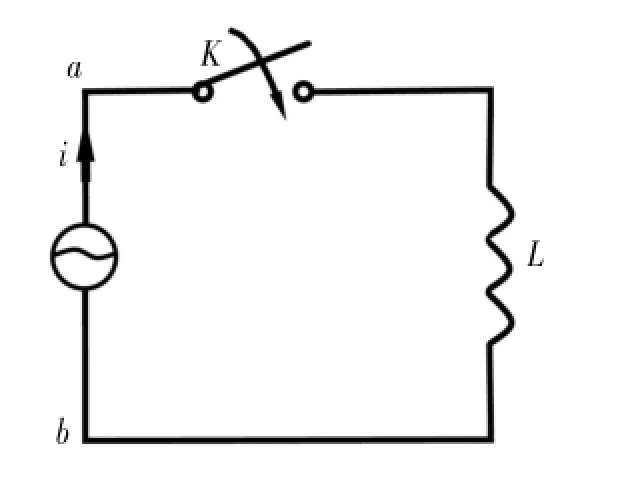
图1　简谐电感线圈电路

电感线圈的自感电动势与电流的关系是

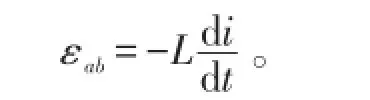
根据基尔霍夫第二定律的实用表述〔4〕，得

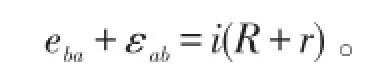
把电源电动势和自感电动势表示式代入其中，整理得

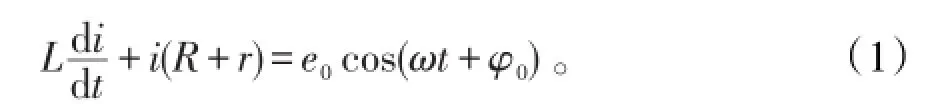
方程（1）的齐次方程的通解为

方程（1）的特解为

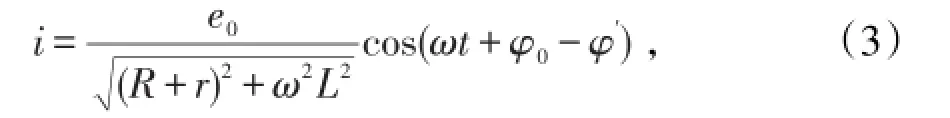
其中

故方程（1）的通解是

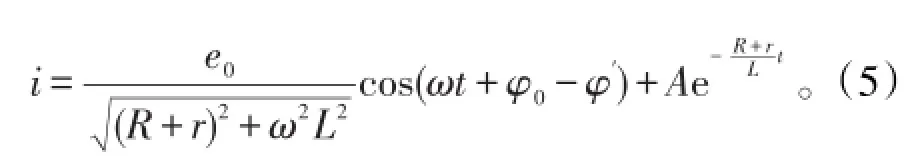
合上电键足够长时间后，指数项衰减到可以忽略的程度，此时

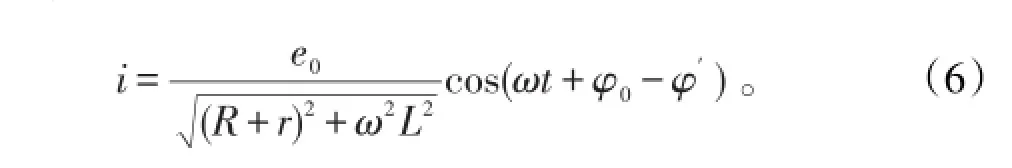
根据含源情形的欧姆定律的微分形式可以推出，路端电压〔4〕

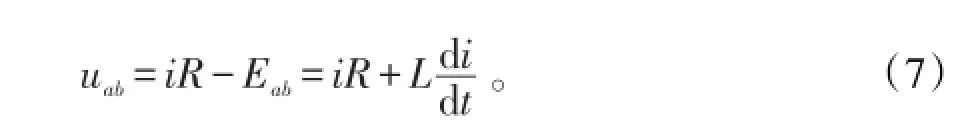
把式（6）代入其中，得

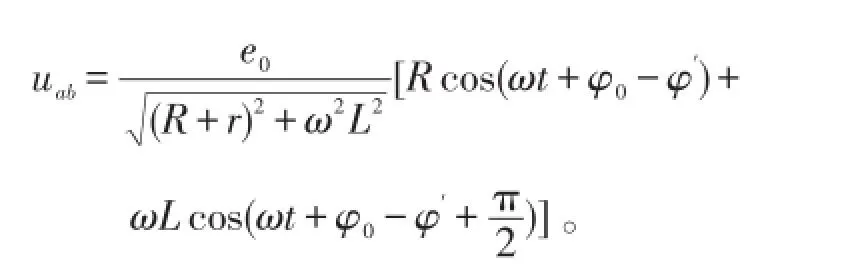
经整理，得

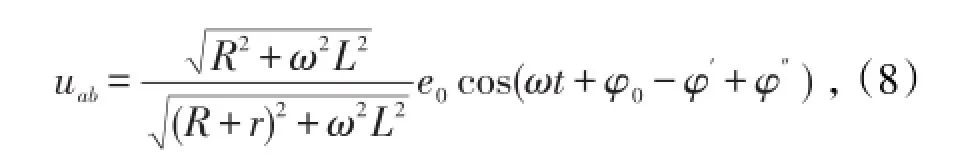
其中

根据式（6）和式（8）知道，流过电感线圈的电流和其路端电压为余弦函数的情况是存在的：当电感线圈和简谐电源接通足够长的时间后，电流和电压就都成了余弦函数。所经历的过程叫做暂态过程。

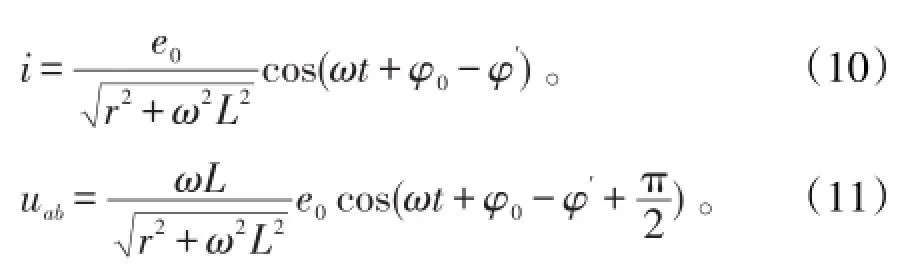
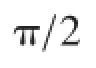
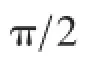
如等式（8）所示，我们已经证明了电感线圈的路端电压为余弦函数是可能的，那么我们就来看看以此为前提该如何推导纯电感线圈的电流与相位关系。

2　路端电压为余弦函数的前提下对纯电感线圈的分析

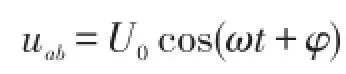
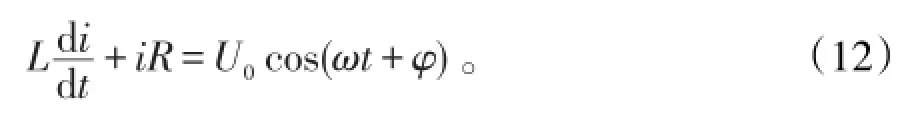
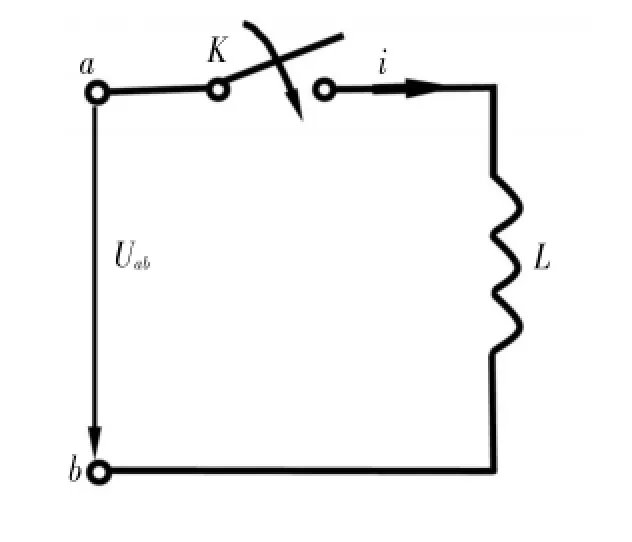
图2　纯电感线圈电路

式（12）的齐次方程的通解为

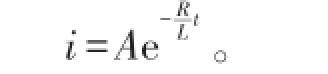
式（12）的特解为

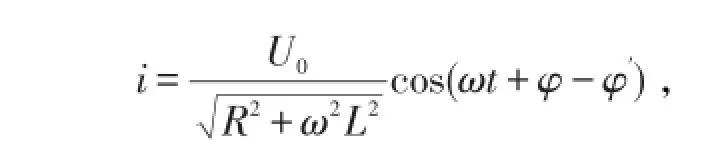
故式（12）的通解为

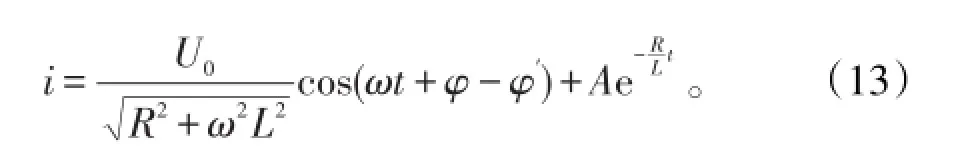
当R≠0时，通电时间足够长后，总有

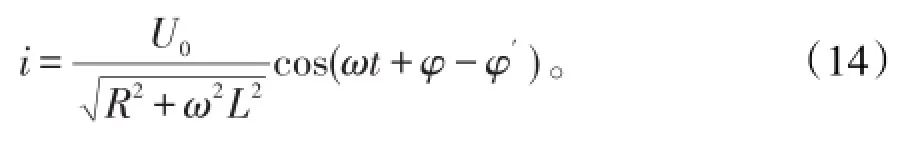
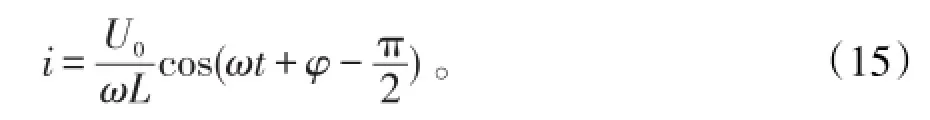
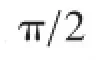
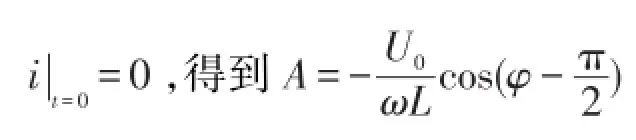
如果选择电压的初相位φ=0，可使A=0。也就是说，必须在纯电感线圈接入电路的时刻它的路端电压的相位恰好等于零这种特殊情况下，才能让A=0。

〔1〕梁灿彬，秦光戎，梁竹健.电磁学〔M〕.北京：高等教育出版社，1980：504-511.

〔2〕哈里德，瑞斯尼克.物理学：第2卷〔M〕.2版.北京：科学出版社，1981：427-429.

〔3〕刘克哲.物理学：下册〔M〕.北京：高等教育出版社，1987：177-178.

〔4〕罗凌霄.基尔霍夫第二定律的实用表述以及建立均匀传输线方程的新途径〔J〕.大学物理，2015，34（7）：6-10.

〔5〕吕旌阳，望育梅，马金明，等.电路分析基础〔M〕.2版.北京：北京邮电大学出版社，2008：73-74.

〔6〕郭硕鸿.电动力学〔M〕.3版.北京：高等教育出版社，2008：92-96.

〔Abstract〕By means of two approaches，this paper strictly proved the phase relation between current and terminal voltage of pure inductance coil，and provided the definition of the easy-operation of pure inductance coil.

〔Key words〕pure inductance coil；current；terminal voltage；phase relation

（责任编辑袁霞）

Phase Relation between Terminal Voltage and Current of Pure Inductance Coil

Peng Jianrong，Luo Lingxiao
（College of Engineering，Dali University，Dali，Yunnan 671003，China）

TM131.2

A

2096-2266（2016）06-0027-03

2016-04-12

2016-05-06

彭建荣，副教授，主要从事电机学研究.