Dn中完全正则半群的结构

周绍艳

（大理大学数学与计算机学院，云南大理　671003）

Dn中完全正则半群的结构

周绍艳

（大理大学数学与计算机学院，云南大理671003）

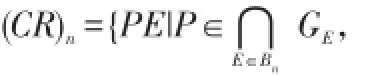
正则元；完全正则元；幂等元；置换阵

［DOI］10. 3969 / j. issn. 2096-2266. 2016. 06. 001

1　引言及预备知识

非负n×n实矩阵D称为双随机矩阵，如果D的每行、每列元素之和为1；全体n×n双随机矩阵构成的集合关于矩阵的乘法构成一个半群，称为双随机矩阵半群，记为Dn。每行、每列只有一个非零元1的双随机矩阵称为置换矩阵；所有n×n置换矩阵构成的集合关于矩阵的乘法构成一个群，称为置换群，记为Pn。

设S是半群，元a∈S称为正则元，如果存在x∈S，使得axa=a成立；元x∈S称为a∈S的逆元，如果axa=a与xax=x均成立；元a∈S称为完全正则元，如果存在x∈S，使得axa=a及ax=xa均成立。如果半群S中的所有元均为正则元，则S称为正则半群；若半群S中的元均为完全正则元，则称S为完全正则半群。在本文中P′是指P的转置矩阵，E（Dn）是指Dn中所有幂等元集。其他未说明的符号及概念参见文献〔1-3〕。

文献〔2〕与〔4-6〕研究了Dn中的幂等元与正则元，不仅给出了幂等元的结构、形式及幂等元之积仍是幂等元的充要条件，还给出了Dn带的结构等结论，从中易得如下引理。

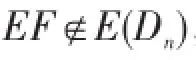
引理2 设E、F∈E（Dn），若EF∈E（Dn），则EF= FE。

引理3如果A∈Dn是正则元，那么A′是它唯一的逆元〔3〕。

引理4A∈Dn是正则元当且仅当存在P∈Pn及E、F∈E（Dn），使得A=EP=PF〔5〕。

2　主要结果

定理1设A∈Dn是正则元，下列条件等价：

（1）A是完全正则元；

（2）AA′=A′A；

（3）A=EP=PE，其中E=AA′，P∈Pn。

证明：由定义及引理3易知（1）与（2）等价。

下证（2）与（3）等价即可。

“（2）⇒（3）”因A是正则元，由引理4、文献〔6〕知：

存在P∈Pn及E=AA′∈E（Dn），使得A=EP。

故AA′=EP（EP）′=EPP′E=E，A′A=（EP）′EP= P′EEP=P′EP。

由AA′=A′A得：E=P′EP，从而PE=EP，即A= EP=PE。

“（3）⇒（2）”由A=EP=PE得：

AA′=EP（EP）′=EPP′E=E，

A′A=（PE）′PE=EP′PE=E。

即AA′=A′A。

定理2 2设A=EP=PF，其中P∈Pn及E、F∈E（Dn）。如果E≠F，则A不是Dn中的完全正则元。

证明：因为A=EP=PP′EP=PF，由幂等元及置换矩阵的性质知P′EP=F。

若E≠F，即P′EP≠E，则PE≠EP。

由引理4、定理1知A不是Dn中的完全正则元。

注1 1Dn中的幂等元是完全正则元，但Dn中的完全正则元未必是幂等元。如：

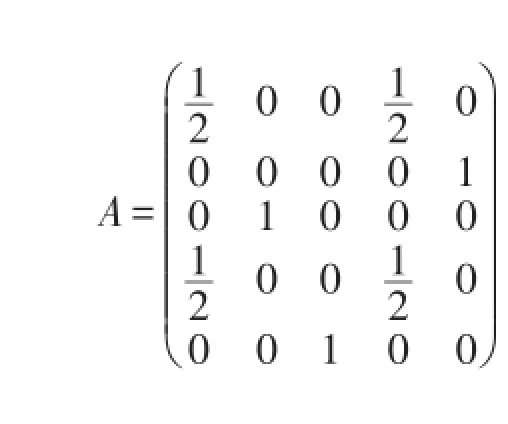
即A不是幂等元。

注2A∈Dn是正则元，若A=A′，则A显然是完全正则元；但若A∈Dn是完全正则元，则未必有A=A′。如注1，A是完全正则元，但A≠A′。

注3完全正则元是正则元，但正则元未必都是完全正则元。如：

但AA′≠A′A，即A不是完全正则元。

定理3Dn中的完全正则元集为：｛PE|PEP′= E，P∈Pn，E∈E（Dn）｝。

证明：由定理1、2及置换阵的性质知结论显然成立。

定理4设E∈E（Dn），GE=｛P∈Pn|EP=PE｝，则GE是Pn的子群。

证明：（1）GE非空且有单位元I，因为Pn中的单位矩阵I∈GE。

（2）对∀P、Q∈GE有EP=PE及EQ=QE，从而有P′EP=E及Q′EQ=E。

于是PQE=PQQ′EQ=PEQ=PP′EPQ=EPQ，故PQ∈GE。

（3）对∀P∈GE有EP=PE，从而（EP）′=（PE）′，即EP′=P′E。

所以P′∈GE，即P有逆元P′∈GE。

再由矩阵乘法满足结合律知GE是Pn的子群。

证明：（必要性）

对∀E、F∈Bn，若EF∉Bn，则由引理1知EF不是正则元。

这与（CR）n是完全正则半群矛盾。故EF∈Bn，即Bn是带。

由引理2知Bn是半格。

（充分性）

由定理1、3知（CR）n中的元均为完全正则元。

要证明（CR）n是完全正则半群，只需证明（CR）n是半群即可。

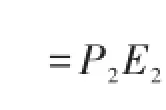
从而AB=P1E1E2P2，BA=P2E2E1P1。

由Bn是半格知E1E2=E2E1∈Bn，记为E。

故AB=P1EP2=P1EP1′P1P2=EP，其中P=P1P2。

即AB∈（CR）n，故（CR）n是半群，从而是完全正则半群。

〔1〕HOWIE J M.An Introduction to Semigroup Theory〔M〕. London：Academic Press，1976.

〔2〕ZHOU Shaoyan，ZHANG Ronghua.The Semilattice of Semigroup of Doubly Stochastic Matrices Dn〔J〕.Journal of Applied Algebral and Discrete Structures，2003，1（2）：119-133.

〔3〕BERMAN A，PLEMMONS R J.Nonnegative Matrices in the Mathematical Science〔M〕.New York：Academic Press，1979.

〔4〕ZHOU Shaoyan，ZHANG Ronghua.A Relation of Idempotent Matrices in Dn〔J〕.Journal of Mathematical Study，2003，36（4）：384-387.

〔5〕周绍艳，张朝元.Dn与正则元有关的两类半群的结构〔J〕.大理学院学报，2015，14（6）：11-12.

〔6〕周绍艳，张荣华.Dn中Clifford半群的结构〔J〕.西南大学学报（自然科学版），2008，30（6）：7-9.

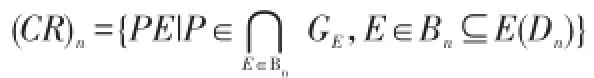
〔Key words〕regular；completely regular element；idempotent；permutation matrix

（责任编辑袁霞）

The Structure of the Completely Regular Semigroup in Dn

Zhou Shaoyan
（College of Mathematics and Computer，Dali University，Dali，Yunnan 671003，China）

O152.7

A

2096-2266（2016）06-0001-03

云南省教育厅科学研究基金资助项目（2012Y151）

2015-11-26

周绍艳，副教授，主要从事代数研究．