锌漆薄膜/2Cr13不锈钢基体薄膜裂纹间距与厚度关系

王成龙　孙　浩　李明玮　杨　健

(河海大学 土木与交通学院， 南京　210098)



锌漆薄膜/2Cr13不锈钢基体薄膜裂纹间距与厚度关系

王成龙孙浩李明玮杨健

(河海大学 土木与交通学院， 南京210098)

以锌漆薄膜/2Cr13不锈钢基体材料为对象，采用拉伸试验与理论分析相结合的方法，研究了不锈钢基体薄膜裂纹间距与厚度关系以及薄膜临界厚度问题．研究结果表明：张拉应变一定时，薄膜存在一个临界厚度．当薄膜厚度小于该临界厚度时，薄膜中不会有裂纹产生，应变越大，临界厚度越小；当薄膜厚度大于临界值时，随着薄膜厚度增加，薄膜裂纹间距也随之增大，二者近似线性相关．对于同一薄膜厚度，随着拉伸荷载持续增加，新裂纹不断出现，裂纹间距不断减小．最终表面裂纹达到饱和状态，裂纹分布呈周期性．

薄膜/不锈钢基体；拉伸试验；周期性裂纹；临界厚度；裂纹间距

大跨度斜拉桥是现代主要桥型，作为斜拉桥主要承重构件，缆索使用寿命对桥梁的安全使用意义重大．为防止缆索腐蚀而大幅降低承载力，一般在缆索表面镀一层保护膜．索体钢丝与表面镀层共同组成了一个薄膜/基体系统．目前国内外学者对于薄膜机理，特别是薄膜断裂问题做了大量的研究，并取得了许多突破性的成果．自1980年以来，对于薄膜断裂性能的研究，断裂力学被广泛运用于分析在弹性或者塑性基体上的薄膜失效问题[1-5]．对于不锈钢韧性基底上镀锌膜而言，破坏形式主要有二:其一薄膜的断裂与龟裂；其二薄膜与基体的分层与脱粘．由于薄膜的失效，会导致膜/基系统可靠度降低甚至影响基体寿命．因此对薄膜力学性能及开裂问题的研究显得尤为重要[6-7]．

对于膜/基系统，由于温度变化、外力等因素作用导致薄膜出现拉应力，当拉应力超过临界值时，薄膜中会产生一系列垂直于界面的周期性裂纹．随着拉应力持续增加，新的裂纹会不断出现，直到裂纹间距达到饱和状态[8-9]．该机理被广泛运用于计算界面抗剪强度[10-11]、薄膜弹性模量和断裂韧性[12-13]．众多学者运用试验方法研究薄膜断裂性能与薄膜几何特征、膜/基力学特性以及界面条件关系[14-15]．附着于基体的薄膜在相同应力下，其裂纹间距与薄膜厚度有一定的关系．在一定拉力作用下通过控制薄膜的厚度，可有效防止薄膜因拉应力而产生裂纹．因此研究薄膜周期裂纹间距与厚度间的关系对于缆索薄膜/基体系统具有重要意义．

本文采用拉伸试验与理论分析相结合的方法，研究在不同的拉应变下，薄膜厚度对于薄膜周期性裂纹间距的影响，并对薄膜临界厚度和拉应力的关系进行了研究．

1　试验工况

锌漆薄膜/不锈钢基体的制作方法是在不锈钢基体上涂刷含高锌量的冷镀锌漆，选取厚度符合需要的试样．此处试件采用矩形截面．选取2Cr13不锈钢作为基体尺寸为25 mm×10 mm×3 mm．在基体的一个25 mm×10 mm面上涂刷锌漆涂层，如图1所示．涂层厚度分别有80 μm、120 μm、160 μm、200 μm和240 μm 5种．拉伸试验在万能试验机上进行，如图2所示．具体加载时，控制试件应变分别为0.4%、0.5%、0.6%、0.8%和1%五种．具体试验工况见表1．由于锌漆薄膜/2Cr13不锈钢基体薄膜贯通裂纹可以达到一个稳态，可将其简化为二维平面问题进行分析．

图1　附着涂层的拉伸试件　　　图2　试件拉伸试验

基体尺寸薄膜厚度/m拉伸应变/%试件个数编号250mm×10mm×3mm2400.431-30.534-60.637-90.8310-121.0313-15

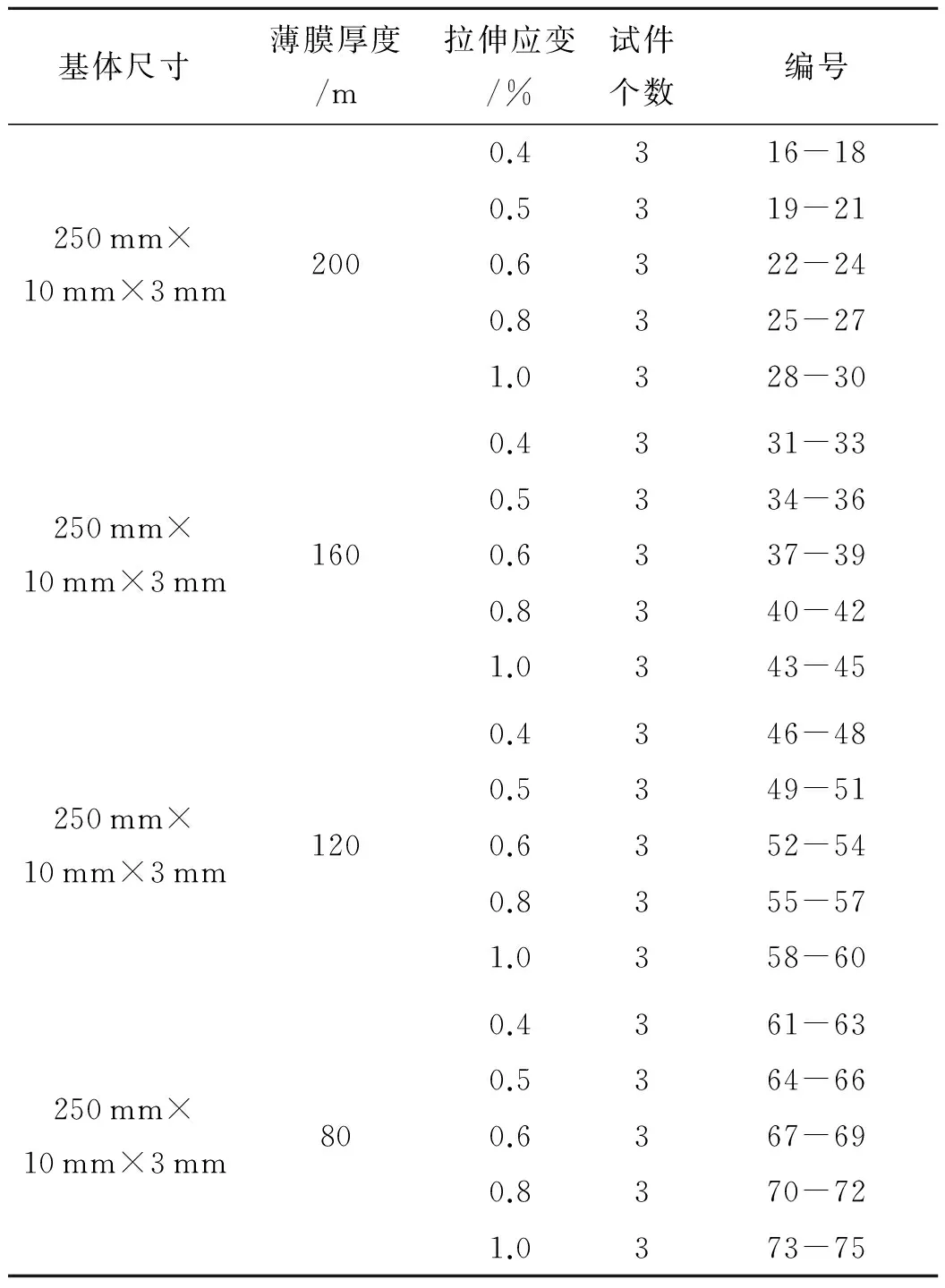
续表1　拉伸试验工况

膜/基结合体系在拉伸荷载作用下，当薄膜应力达到临界值时，裂纹首先在薄膜缺陷处产生并扩展至界面．随着荷载的增加，两条平行的表面裂纹之间会产生新的裂纹，随着载荷的增加裂纹数量增加，直至达到饱和．试验时，通过显微镜测量一段距离内裂纹的条数来计算薄膜裂纹间距．拉伸实验用到的万能试验机型号为CSS44100，通过夹具将试件两端夹紧，两夹具之间的距离为200 mm．采用位移加载方式，加载速度为0.4 mm/min．加载过程中，始终认为薄膜与基体的纵向应变相同，即为拉伸位移与夹具距离的比值．加载后，薄膜/基体试件会产生一系列薄膜表面垂直裂纹，且这些裂纹间距有一定规律，可近似为周期性．如图3，显微镜观测图显示了试件加载后在薄膜中产生的一系列周期裂纹．

图3　试件拉伸后的薄膜周期裂纹显微镜观测照片

2　试验结果与分析

分别对0.4%、0.5%、0.6%、0.8%和1% 5种应变下，薄膜周期裂纹间距进行分析，得出裂纹间距与薄膜厚度的一些关系．各应变下的试验结果见表2．

表2　试件各应变下不同薄膜厚度对应的裂纹间距

试件拉伸应变为0.4%时，只有薄膜厚度为240 μm和200 μm两种膜/基试件会产生周期薄膜裂纹．而薄膜厚度小于200 μm的三种膜/基试件并未产生周期裂纹，这说明在应变为0.4%时，对应薄膜厚度为160 μm、120 μm和80 μm的试件并未达到薄膜临界应变，这也进一步说明薄膜张拉强度不仅取决于材料本身的属性，还与薄膜厚度有关．拉伸应变为0.5%和0.6%时，对于薄膜厚度为240 μm、200 μm和160 μm的试件，均产生了周期裂纹，对于薄膜厚度为120 μm和80 μm的试件，均未产生周期裂纹，即未达到薄膜临界应变．

拉伸应变为0.6%、0.8%和1.0%时薄膜周期裂纹间距与薄膜厚度的关系曲线分别如图4(a)、(b)和(c)所示，图中λ表示裂纹间距，h表示薄膜厚度．图4中不论理论解答[7]还是试验结果都表明：(a)在同样的应变下，当薄膜厚度大于临界厚度时，随着薄膜厚度的增大，薄膜周期裂纹间距也变得越大；二者接近线性关系且薄膜存在一个临界厚度，当薄膜厚度小于该临界厚度时，薄膜中不会有周期裂纹产生．如应变为0.6%情况下，临界厚度介于800 μm到120 μm之间．而应变为0.8%和1%的情况下，临界厚度均小于80 μm；(b)在同一薄膜厚度下，随着拉应变增加，薄膜周期裂纹间距会变得越小；(c)拉应变大于0.8%、厚度大于160 μm，试验值和理论中吻合较好．对于同一厚度的薄膜，一次裂纹萌生后，对于同一厚度的薄膜随着拉伸荷载的不断增加，也会不断产生新的裂纹，使裂纹间距不断减小．

图5显示了240 μm厚薄膜裂纹间距随荷载变化的曲线图．当然，实际裂纹开裂时，裂纹间距的变化并不是一条密实的曲线，而是一个个离散的点．当两条裂纹之间的薄膜在缺陷处其能量释放率大于薄膜断裂韧性时，就会在该处产生新的裂纹．然而，实际情况下薄膜上的一系列裂纹并不是严格意义上的周期裂纹，因此，对已有裂纹而言，新生裂纹并非在同一时刻产生．

图4　裂纹间距与薄膜厚度的关系

由图5可以发现，随着荷载不断增加，薄膜中新表面裂纹持续产生，但表面裂纹最终会达到一个饱和值．若此时荷载继续增加，将沿着薄膜与基体界面产生裂纹．

图5　240 μm厚薄膜裂纹间距随应变变化的曲线图

图6　弹性基体情况下薄膜临界断裂强度与裂纹间距和薄膜厚度比的关系

3　薄膜临界厚度的分析

关于薄膜临界厚度，前面已经提到，即给定薄膜断裂韧性和张拉应力，存在一个临界厚度，当薄膜的厚度小于该临界厚度时，在薄膜中不会有裂纹产生．临界厚度[13]根据已有公式可表示为

从上式可以看出，薄膜临界厚度与薄膜断裂韧性和参数c成正比，可知基体弹性模量越小，临界厚度也就越小．图7为薄膜临界厚度与薄膜拉伸应变之间的相互关系．可以看出，薄膜临界厚度与拉伸应变呈双曲线关系，应变越大，临界厚度越小，εcr值小于0.5%时，随着应变的增大临界厚度急剧减小，εcr值大于1.5%时，渐渐趋缓．分别计算薄膜应变为0.4%、0.5%、0.6%、0.8%和1%下薄膜的临界厚度，计算结果示于表3．与前面的试验结果进行比较，如应变为0.4%时，200 μm厚度的薄膜出现裂纹，而160 μm厚度的薄膜未出现裂纹，与理论计算结果有出入；应变为0.5%时，160 μm厚度薄膜出现裂纹，而120 μm厚度薄膜未出现裂纹，与理论计算结果吻合；应变0.6%情况下，临界厚度在120 μm和80 μm之间，试件结果与理论结果相吻合；应变为0.75%和1%的情况，在80 μm后薄膜上均已出现裂纹，临界厚度应小于80 μm，试验结果与理论结果也基本吻合．从表中还可看出，薄膜临界厚度随拉力的增大而不断减小．

图7　薄膜临界厚度与薄膜拉伸应变的相互关系

应变/%0.40.50.60.81.0临界厚度/m2281461016536

4　结　论

本文对不同薄膜厚度的锌漆薄膜/2Cr13不锈钢基体进行了拉伸试验，分析了薄膜厚度与裂纹间距的相互关系，并对薄膜的临界厚度问题进行了研究．得出以下结论：

1)张拉应变一定时，薄膜存在一个临界厚度．当薄膜厚度小于该临界厚度时，薄膜中不会有裂纹产生．应变越大，临界厚度越小．通过对比，发现试验结果与理论结果基本吻合．

2)在相同张拉应变下，当薄膜厚度大于临界厚度时，随着薄膜厚度的增大，薄膜周期裂纹间距也有增大趋势，二者几乎呈线性关系．

3)同一厚度的薄膜，一次裂纹萌生后，随着拉伸荷载的不断增加，会不断产生新的裂纹，使裂纹间距不断减小．最终薄膜表面裂纹会达到饱和，裂纹间距分布呈周期性，转而产生薄膜与基体之间的界面裂纹．

4)利用临界厚度理论公式计算出不同拉应变下的锌漆薄膜临界厚度，分析得出试验结果与理论结果吻合，薄膜临界厚度随拉力的增大而不断减少．

[1]Thouless M D， Evans A G， Ashby M F, et al. The Edge Cracking and Spalling of Brittle Plates[J]． Acta Metallurgica, 1987, 35(6)：1333-1341．

[2]Ye T, Suo Z, Evans A G. Thin Film Cracking and the Roles of Substrate and Interface[J]． International Journal of Solids and Structures, 1992, 29(21)：2639-2648．

[3]Beuth J L, Klingbeil N W. Cracking of Thin Films Bonded to Elastic-plastic Substrates[J]． Journal of the Mechanics and Physics of Solids, 1996, 44(9)：1411-1428．

[4]Ldrissi H, Wang B, Colla M S, et al. Ultrahigh Strain Hardening in Thin Palladium Films with Nanoscale Twins[J]． Advanced Materials, 2011, 23(18)： 2119-2122．

[5]Matoy K, Detzel T, Müller M, et al. Interface Fracture Properties of Thin Films Studied by Using the Micro-cantilever Deflection Technique[J]． Surface and Coatings Technology, 2009, 204(6)：878-881．

[6]Parmigiani J P, Thouless M D. The roles of Toughness and Cohesive Strength on Crack Deflection at Interfaces[J]． Journal of the Mechanics and Physics of Solids, 2006, 54(2)：266-287．

[7]Mei H, Pang Y, Huang R. Influence of Interfacial Delamination on Channel Cracking of Elastic Thin Films[J]． International Journal of Fracture, 2007, 148(4)：331-342．

[8]Yin H M, Buttlar W G, Paulino G H. Simplified Solution for Periodic Thermal Discontinuities in Asphalt Overlays Bonded to Rigid Pavements[J]． Journal of Transportation Engineering, 2007, 133(1)：39-46．

[9]Xia Z C, Hutchinson J W. Crack Patterns in Thin Films[J]． Journal of the Mechanics and Physics of Solids, 2000, 48(6)：1107-1131．

[10] Agrawal D C, Raj R. Measurement of the Ultimate Shear Strength of a Metal-ceramic Interface[J]． Acta Metallurgica, 1989, 37(4)：1265-1270．

[11] Leevers P S, Godart M A. Adiabatic Decohesion in a Thermoplastic Craze Thickening at Constant or Increasing Rate [J]． Journal of the Mechanics and Physics of Solids, 2008, 56(6)：2149-2170．

[12] Tadepalli R, Turner K T, Thompson C V. Mixed-mode Interface Toughness of Wafer-level Cu-Cu Bonds Using Asymmetric Chevron tTest[J]． Journal of the Mechanics and Physics of Solids, 2008, 56(3)：707-718．

[13] Parmigiani J P, Thouless M D. Theroles of Toughness and Cohesive Strength on Crack Deflection at Interfaces[J]． Journal of the Mechanics and Physics of Solids, 2006, 54(2)：266-287．

[14] Thouless M D, Olsson E, Gupta A. Cracking of Brittle Films on Elastic Substrates[J]． Acta Metallurgica et Materialia, 1992, 40(6)：1287-1292．

[15] Wang Y, Kanjanaboos P, Barry E, et al. Fracture and Failure of Nanoparticle Monolayers and Multilayers[J]． Nano Letters, 2014, 14(2)：826-830．

[责任编辑周文凯]

Relation Between Film Crack Spacing and Thickness for a Zinc Paint Film Bonded to 2Cr13 Stainless Steel Substrate

Wang ChenglongSun HaoLi MingweiYang Jian

(College of Civil & Transportation Engineering, Hohai Univ., Naijing 210098, China)

A tensile experiment with theoretical analysis is carried out to investigate the relation between crack spacing and film thickness and analyze film critical thickness of the zinc paint film bonded to 2Cr13 stainless steel substrate. The results show that under a certain tensile strain, a critical thickness exists. When the film thickness is less than the critical thickness, a crack fails to initiate. With the increasing tensile strain, critical thickness becomes smaller. When the film thickness is larger than the critical thickness, with the increasing film thickness, the crack spacing also becomes larger and approximate linear correlation. For the same film thickness, additional cracks will form and crack spacing decreases continuously if the tensile stress increases. Finally, the saturation spacing is reached and cracks distribute periodically.

film/stainless steel substrate;tension test;periodic cracks;critical thickness;crack spacing

2016-03-22

王成龙(1990-)，男，硕士研究生，主要研究方向为桥梁缆索镀层开裂机理．E-mail： 1054158346@qq.com

10.13393/j.cnki.issn.1672-948X.2016.04.011

TU392.2

A

1672-948X(2016)04-0051-04