三跨斜交简支梁桥地震碰撞反应参数影响研究

湛　敏　王军文　闫聚考　王　肖

(1. 石家庄铁道大学 土木工程学院， 石家庄　050043； 2. 石家庄铁道大学 大型结构健康诊断与控制研究所， 石家庄　050043； 3. 重庆交通大学 土木工程学院， 重庆　400074)



三跨斜交简支梁桥地震碰撞反应参数影响研究

湛敏1王军文1闫聚考2王肖3

(1. 石家庄铁道大学 土木工程学院， 石家庄050043； 2. 石家庄铁道大学 大型结构健康诊断与控制研究所， 石家庄050043； 3. 重庆交通大学 土木工程学院， 重庆400074)

利用OpenSees地震仿真模拟平台，建立了3×30 m斜交简支梁桥计算模型，通过改变斜度、纵向伸缩缝间隙、梁体与横向挡块间初始间隙，研究结构地震碰撞反应的变化规律，研究发现：桥面峰值转角随斜度和伸缩缝间隙增大呈现先增大后减小的变化规律，随横向初始间隙增大而逐渐增大；梁体纵向最大位移随斜度和伸缩缝间隙增大而逐渐增大，随横向初始间隙增大呈现先减小后增大的变化规律；墩底最大反力和墩顶顺桥向最大位移的变化规律与梁体纵向最大位移的变化规律一致．

斜交桥；简支梁；地震碰撞；参数分析

斜交桥在公路、铁路以及城市道路桥梁中是一种常见桥型，由于斜交桥独特的结构外形和受力特性，地震破坏要比正交桥更为严重，而梁体碰撞破坏则是较为常见的震害之一．如1999年美国Hector Mine地震中Pisgah高架桥在桥台处遭到碰撞破坏；1999年墨西哥Tehuacan地震中多数斜交桥上部结构与横向挡块之间发生横向碰撞，导致挡块严重破坏[1]；2008年汶川大地震中，绵竹市新东桥发生桥面旋转现象，并在锐角处发生碰撞损伤，平武县的南坝桥梁体发生严重的横向位移，导致横向挡块碰撞破坏并最终引发落梁震害[2]．

近年来，学者们针对斜交桥地震反应进行了很多相关研究．Meng[3]研究发现：支承墩柱的地震内力和上部结构位移均随斜度增大而增大；刘鹏[4]与罗婧文等[5]研究指出：横向挡块初始间隙的设置存在一个最佳值，当其处于最佳值时，对桥面转动效应抑制最明显，而初始间隙与各挡块最大碰撞力之间的关系具有不确定性；文献[6]通过对单跨斜交简支梁桥进行研究，发现纵向位移峰值随斜度增大而增大，桥面峰值转角随斜度增大呈现先增大后减小的变化趋势；邓志荣[7]针对单跨和多跨斜交桥地震反应进行研究，研究认为，桥梁斜度大于25°时，梁体位移和墩底内力随斜度的增大而增大；卓秋林[8]分析探讨了斜度、墩高和跨径对多跨斜交简支桥地震反应的影响，分析指出，斜度越大、墩高越高、跨径越大，上部结构位移和墩底内力越大．可以看出，很多学者针对斜交桥地震反应的参数影响进行了大量研究，但鲜有文献针对多跨斜交简支梁桥地震碰撞参数影响进行研究．为此，本文借助OpenSees软件，建立三跨斜交简支梁桥计算模型，研究在考虑纵、横向碰撞作用情况下，斜度和纵、横向初始间隙变化对结构地震碰撞反应的影响．

1　计算模型及地震动输入

本文以一座3×30 m斜交简支梁桥作为研究对象．该桥上部结构采用4片预制小箱梁拼装，桥面宽12 m，横隔板每跨共设置6道；采用重力式桥台，中间两桥墩采用双柱式圆形墩，盖梁采用矩形截面；主梁每端设置8块板式橡胶支座，支座剪切刚度取4.37×103kN/m．利用美国伯克利大学开发的OpenSees软件进行数值模拟，斜交桥上部结构采用梁杆模型简化，如图1所示，α为斜交角．

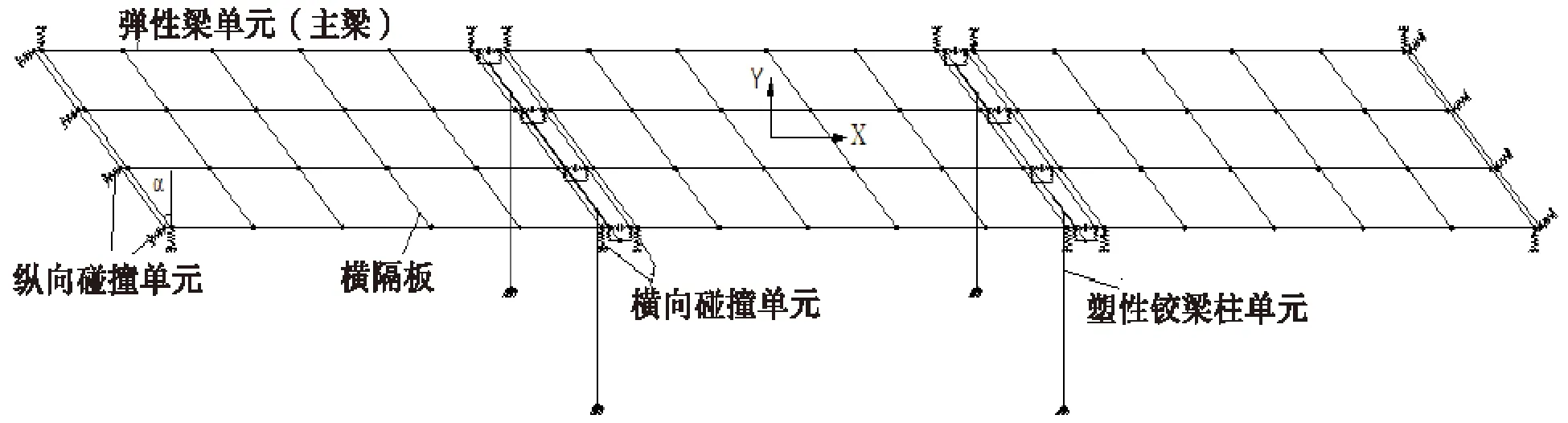
图1　全桥计算模型

模型中纵梁、横隔梁、盖梁均采用弹性梁柱单元模拟，支座采用零长度(Zero Length)单元模拟，桥墩采用塑性铰梁柱单元模拟．利用碰撞材料和零长度单元模拟梁体与刚性桥台间的碰撞，其恢复力模型[9]如图2所示．图中，δy为屈服位移，Keff、Kt1、Kt2分别为碰撞等效刚度、初始刚度和屈后刚度，通过计算，边梁Kt1取5.54×105kN/m，Kt2取1.91×105kN/m；中梁Kt1取5.38×105kN/m，Kt2取1.85×105kN/m；最大侵入深度δm取2.54 cm．利用理想塑性间隙材料(Perfectly Plastic Gap Material)和零长度单元模拟梁体与横向挡块间的碰撞，横向挡块采用的理想弹塑性模型[10]如图3所示．其中，初始刚度K0取5.0×106kN/m，屈服力Fy取1 294 kN．模型梁端设置4个纵向碰撞单元，方向垂直于主梁端部，每个角点处设置1个横向碰撞单元．全桥计算模型如图1所示．

图2 碰撞材料的恢复力模型　图3 挡块的理想弹塑性模型

选取沿与整体坐标系X轴正向夹角分别为0°、45°、60°、120°和180°共5个方向作为地震输入的主方向[6]．从Ⅱ类场地条件中选取7条近场实际地震加速度记录(见表1)，根据规范[11]将地震波加速度峰值调整为0.4g沿选取的斜交桥主方向输入，从中选出最不利的情况，并将计算结果取平均值以分析结构的地震响应．

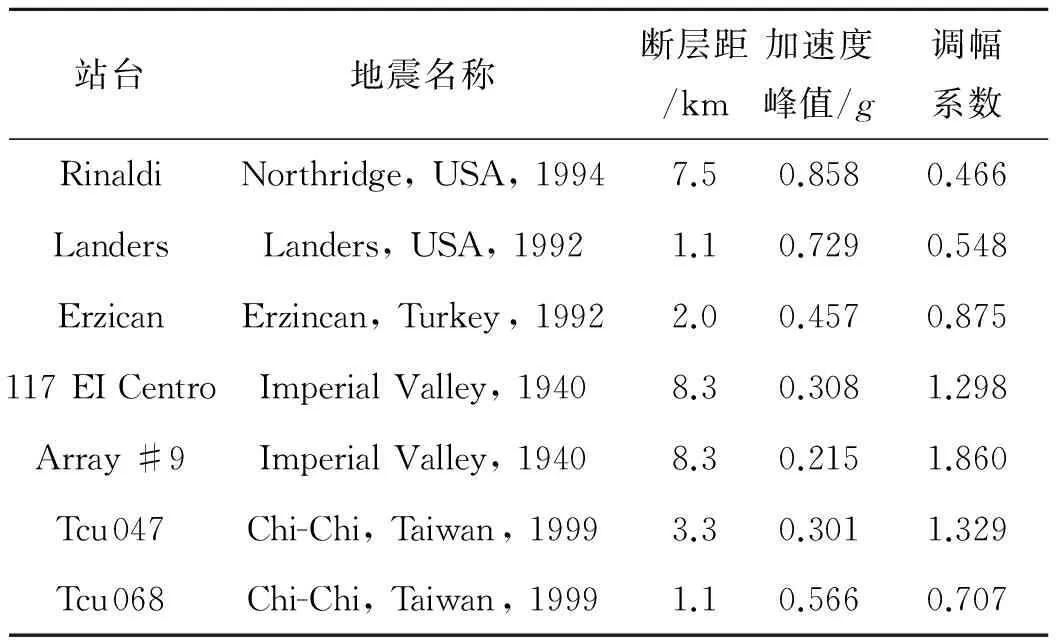
表1　选取的地震波

2　结构参数影响分析

2.1斜度的影响

斜度是斜交桥结构分析的一个重要参数，斜度的变化对于斜交桥动力特性及地震反应具有重要影响．研究本参数时，保持4 cm横向初始间隙和5 cm纵向伸缩缝间隙不变，取斜度0°、15°、30°、45°、60°作为参数，研究斜交桥桥面峰值转角、纵向最大位移、最大碰撞力、墩底最大反力和墩顶最大位移的变化规律．计算结果分别如图4～6和表2所示．

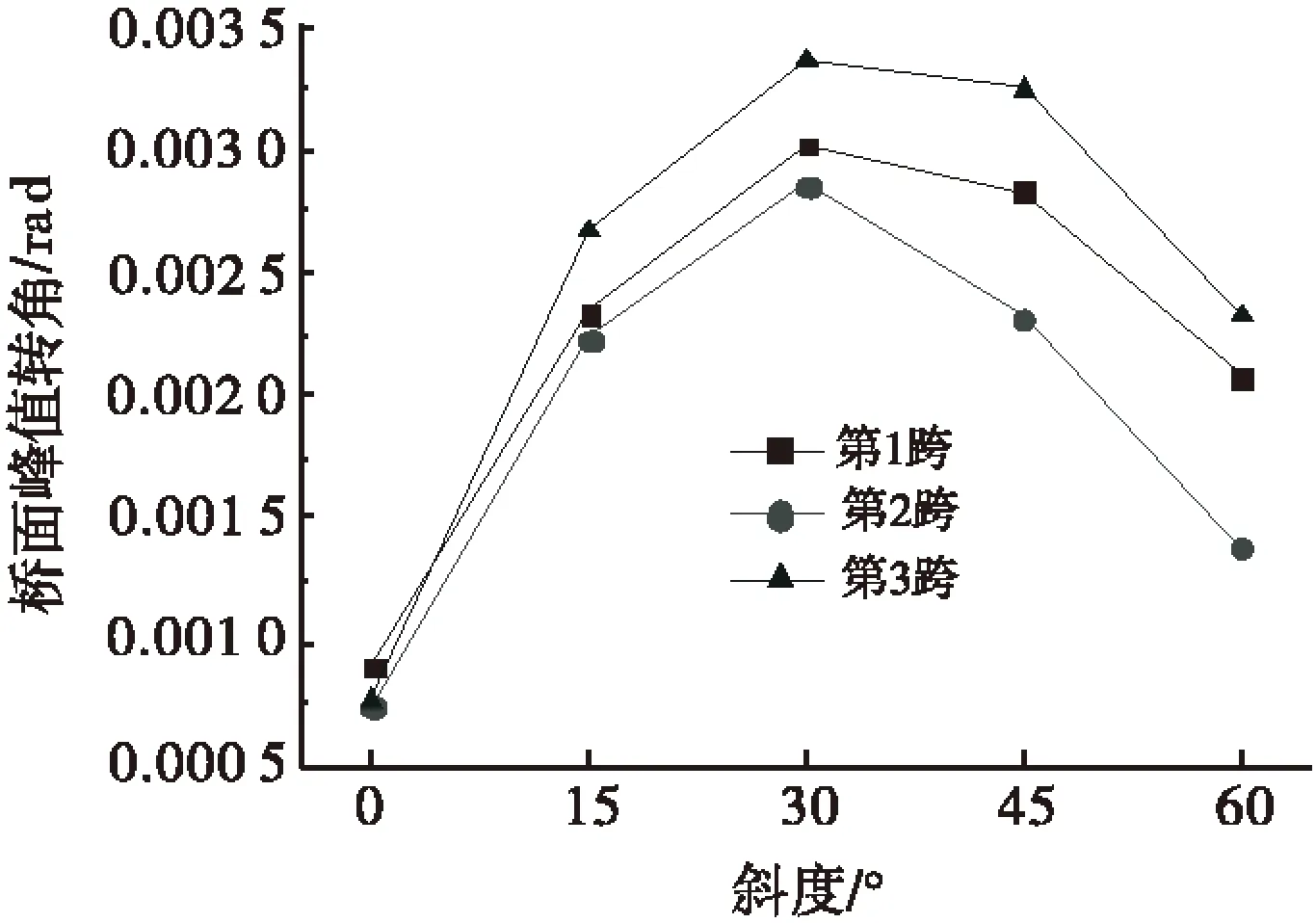
图4　斜度对桥面峰值转角的影响

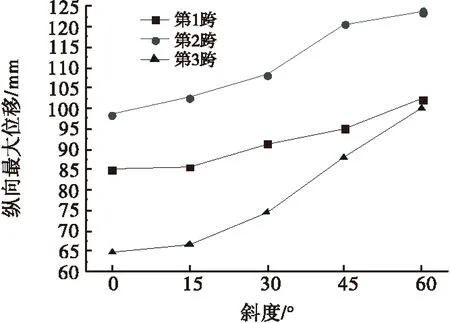
图5　斜度对纵向最大位移的影响

图6　斜度对最大碰撞力的影响

斜度/°剪力/kN弯矩/kN·m扭矩/kN·mX向位移/cmY向位移/cm01169.25384.1808.61.741.44151245.95894.1858.91.861.47301362.46632.7981.21.882.28451450.57374.51009.21.921.81601465.67463.31062.31.982.05

结合图4、图5可以发现，随着斜度增大，桥面峰值转角呈现先增大后减小的变化规律，梁体纵向最大位移则逐渐增大，这与文献[6]得出的结论保持一致；当斜交角为30°时，桥面峰值转角达到最大值，这由斜交桥自身的结构特性及碰撞形式所决定，文献[12]认为，考虑梁体碰撞时，碰撞力产生的力矩是引起斜交桥桥面旋转的主要原因，对于本文所研究的对象，当斜度为30°时，纵向碰撞力最大，所产生的力矩也最大程度地加剧了桥面旋转，因此，桥面峰值转角最大．此外，由于边跨及中跨支承刚度的差异，使得中跨峰值转角始终小于边跨，并随着斜度增大，这种现象愈发明显．同时，中跨纵向最大位移始终大于边跨，最大可高出36.2 mm．

从图6可以看出，最大碰撞力随着斜度增大呈现先增大后减小的变化规律，并且在30°时，达到最大值，其中，横向最大值为1 248 kN，纵向为3 875 kN；边跨纵向最大碰撞力始终大于中跨，最大高出1 289 kN，而横向最大碰撞力并无此规律．由表2可知，墩底最大反力随斜度增大而逐渐增大，这与上述研究成果均保持一致；墩顶X向(顺桥向)最大位移随斜度增大而逐渐增大，Y向(横桥向)最大位移则没有明显的变化规律．

通过以上分析，可以看出，对于斜交简支梁桥，三跨与单跨地震碰撞反应随斜度变化具有相似的变化规律，而对于三跨斜交简支梁桥，在斜度为30°处将产生较大碰撞力并引起较大的桥面旋转．

2.2纵向伸缩缝间隙的影响

相邻梁体间及梁体与桥台间的纵向相对位移超过伸缩缝间隙时，将发生碰撞作用，而合理地设置伸缩缝间隙对于桥梁结构地震碰撞反应有着重要影响．在进行本参数分析时，保持4 cm横向初始间隙和30°斜交角不变，伸缩缝间隙从1～9 cm取值，中间间隔2 cm．计算结果如图7～9和表3所示．

图7　伸缩缝间隙对桥面峰值转角的影响

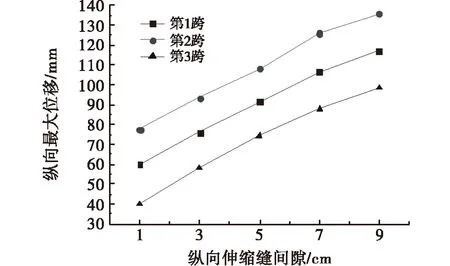
图8　伸缩缝间隙对纵向最大位移的影响

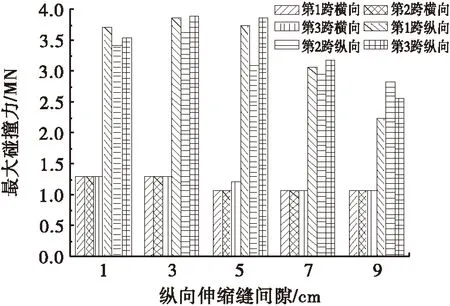
图9　伸缩缝间隙对最大碰撞力的影响

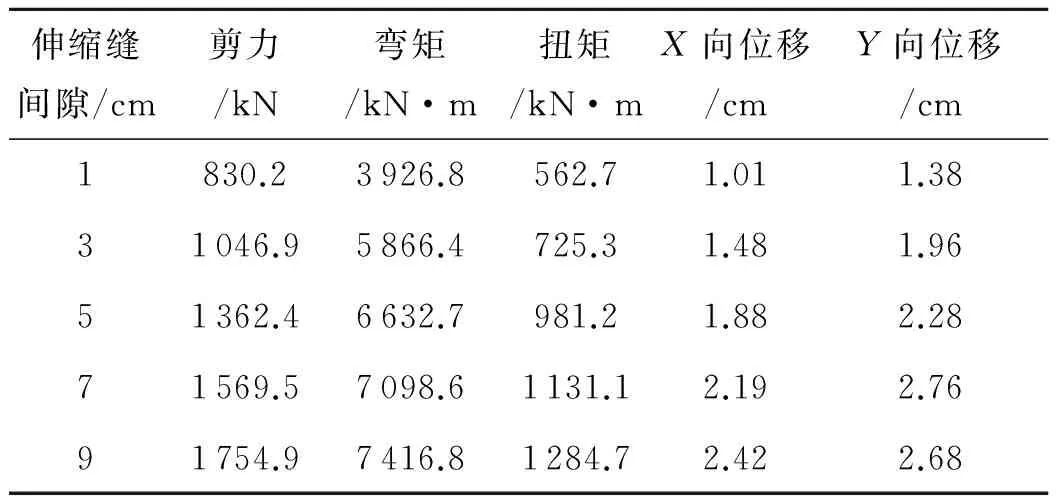
伸缩缝间隙/cm剪力/kN弯矩/kN·m扭矩/kN·mX向位移/cmY向位移/cm1830.23926.8562.71.011.3831046.95866.4725.31.481.9651362.46632.7981.21.882.2871569.57098.61131.12.192.7691754.97416.81284.72.422.68

结合图7、图8可以看出，随着纵向伸缩缝间隙的增大，桥面峰值转角呈现先增大后减小的变化规律，纵向最大位移则几乎呈线性增大，这与文献[13]得出的结论保持一致；当伸缩缝间隙为3 cm时，桥面峰值转角达到最大值，其中，边跨最大值为0.003 61 rad，中跨为0.002 81 rad，边跨桥面峰值转角同样始终要大于中跨．

由图9可知，随着伸缩缝间隙的增大，纵向最大碰撞力呈现先增大后减小的变化规律，并在伸缩缝间隙为3 cm处达到最大值，其中，边跨最大值为3 884 kN，中跨为3 616 kN；横向最大碰撞力逐渐减小，且当伸缩缝间隙不大于3 cm时，横向最大碰撞力达到1 294 kN，超过屈服力Fy，横向挡块破坏．从表3可以看出，随着伸缩缝间隙增大，墩底最大反力和墩顶X向最大位移均逐渐增大，墩顶Y向最大位移则先增大后减小．

通过上述分析可以发现，对于三跨斜交简支梁桥，伸缩缝间隙过小，会引起横向挡块的碰撞破坏，而伸缩缝间隙过大，又将引起较大的桥面纵向位移和墩底反力，易导致落梁震害及墩底破坏．

2.3横向挡块初始间隙的影响

横向挡块是桥梁抗震设计的重要组成部分，横向挡块初始间隙的设置则直接影响其抗震性能．在进行该参数研究时，保持3 cm纵向伸缩缝间隙和30°斜交角不变，横向初始间隙从2～10 cm取值，中间间隔2 cm，计算结果如图10～12和表4所示．

图10　横向初始间隙对桥面峰值转角的影响

图11　横向初始间隙对纵向最大位移的影响

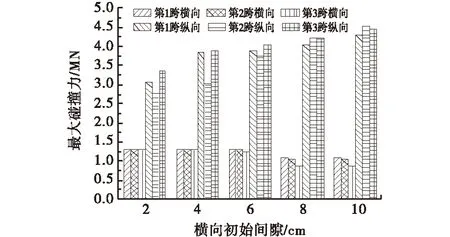
图12　横向初始间隙对最大碰撞力的影响

横向初始间隙/cm剪力/kN弯矩/kN·m扭矩/kN·mX向位移/cmY向位移/cm21115.87153.2767.11.501.9441046.96866.4725.31.481.9661005.96563.1695.31.451.9981033.16965.1712.81.432.01101047.97352.2723.31.632.12

结合图10、图11可知，随着横向初始间隙的增大，桥面峰值转角逐渐增大，而纵向最大位移则呈现先减小后增大的变化规律，这与文献[13]中的结论仍然一致；当横向初始间隙为6 cm时，纵向最大位移达到最小值，其中，中跨为90.52 mm，边跨为50.50 mm．

由图12可知，随着横向初始间隙的增大，纵向最大碰撞力逐渐增大，横向最大碰撞力逐渐减小，并且当横向初始间隙不大于为4 cm时，横向最大碰撞力达到1 294 kN，横向挡块破坏．从表4可以发现，随着横向初始间隙增大，墩底最大反力和墩顶X向最大位移均呈现先减小后增大的变化规律，并在6 cm处达到最小值；墩顶Y向最大位移则逐渐增大．

通过以上分析，可以看出，横向初始间隙较小时，对于抑制桥面旋转具有积极作用，但易发生碰撞破坏，而横向初始间隙对纵向最大位移的影响并不是很大．

3　结　论

通过对三跨斜交简支梁桥地震碰撞反应的变化规律进行研究，可得出如下结论：

1)随着斜度增大，桥面峰值转角和最大碰撞力呈现先增大后减小的变化规律，纵向最大位移、墩底最大反力和墩顶X向最大位移则逐渐增大．

2)随着纵向伸缩缝间隙的增大，桥面峰值转角和纵向最大碰撞力呈现先增大后减小的变化规律，横向最大碰撞力逐渐减小，纵向最大位移、墩底最大反力和墩顶X向最大位移则逐渐增大．

3)随着横向初始间隙的增大，桥面峰值转角、纵向最大碰撞力逐渐增大，横向最大碰撞力逐渐减小，纵向最大位移、墩底最大反力和墩顶X向最大位移则呈现先减小后增大的变化规律．

4)影响三跨斜交简支梁桥地震碰撞反应的因素较多，而在实际中各个因素之间的相互作用对结构地震反应的影响还有待进一步研究．

[1]DIMITRAKOPOULOS E G． Analysis of a Frictional Oblique Impact Observed in Skew Bridges[J]． Nonlinear Dynamics，2010，60(4): 575-594．

[2]杜修力，韩强，李忠献，等．5·12泣川地震中山区公路桥梁震害及启示[J]．北京工业大学学报，2008，34(12):1270-1279．

[3]Meng J Y, Lui E M． Seismic Analysis and Assessment of a Skew Highway Bridge[J]． Engineering Structures, 2000，22(11):1433-1452．

[4]刘鹏．地震作用下桥梁梁体与横向挡块动态碰撞研究[D]．成都:西南交通大学，2007．

[5]罗婧文，左科．地震作用下单跨斜交梁桥碰撞模型反应分析[J]．华东公路，2014(5):61-64．

[6]王军文，吴天宇，闫聚考．斜交简支梁桥地震碰撞反应参数分析[J]．振动与冲击(已录用)．

[7]邓志荣．公路斜交桥地震反应分析[D]．长沙:长沙理工大学，2010．

[8]卓秋林．公路简支斜梁桥地震反应分析[D]．福州:福州大学，2004．

[9]Nielson B G． Analytical Fragility Curves for High-way Bridges in Moderate Seismic Zones(Doctorate Dissertation) [D]． Atlanta: Georgia Institute of Technology，2005．

[10] Silva P F，Megally S，Seible F． Seismic Performance of Sacrificial Exterior Shear Keys in Bridge Abutments[J]． Earthquake Spectra，2009，25(3):643-664．

[11] 公路桥梁抗震设计细则JTG/TB02-01-2008[S]．北京：人民交通出版社，2008．

[12] 王军文，沈贤，李建中．地震作用下斜交简支梁桥旋转机理及斜度影响研究[J]．桥梁建设，2014，44(3):34-40．

[13] 沈贤．地震作用下简支斜交桥桥面旋转机理及影响因素研究[D]．石家庄:石家庄铁道大学，2013．

[责任编辑周文凯]

Parametric Analysis of Three-Span Skewed Simply Supported Girder Bridge under Seismic Collision Response

Zhan Min1Wang Junwen1Yan Jukao2Wang Xiao3

(1. School of Civil Engineering, Shijiazhuang Railway Univ., Shijiazhuang 050043, China； 2. Structural Health Monitoring & Control Institute, Shijiazhuang Railway Univ., Shijiazhuang 050043, China； 3. School of Civil Engineering, Chongqing Jiaotong Univ., Chongqing 400074, China)

A dynamic calculation model of 3×30m skewed simply supported girder bridge is established by using the software OpenSees. The variations of structure under seismic collision response is studied by changing the skew angle, initial gap at expansion joint and initial gap between girder. The results indicate that the peak angle of the deck increases firstly and then decreases with the increase of the skew angle and initial gap at expansion joint, but increases with the increase of initial gap between girder; the maximum longitudinal displacement of the girder increases with the increase of the skew angle and initial gap at expansion joint, but decreases firstly and then increases with the increase of initial gap between girder; the variations of the maximum reverse force and the maximum displacement of pier top along the bridge have the same variations with the longitudinal displacement of the girder.

skewed bridge;simply supported girder;seismic collision;parametric analysis

2016-04-15

河北省自然科学基金项目(E2015210038)；国家青年科学基金项目(51508347)

湛敏(1991-)，男，硕士研究生，研究方向为桥梁抗震．E-mail： njlhzm@163.com

10.13393/j.cnki.issn.1672-948X.2016.04.010

U448.41；U442.55

A

1672-948X(2016)04-0046-05