优化神经网络模型在水质预测中的运用
曹栋华 陈佳袁 刘益志 余松林
(1. 河海大学 水利水电学院, 南京 210098; 2. 江苏省宿迁市水务局,江苏 宿迁 223800)
优化神经网络模型在水质预测中的运用
曹栋华1陈佳袁1刘益志2余松林1
(1. 河海大学 水利水电学院, 南京210098; 2. 江苏省宿迁市水务局,江苏 宿迁223800)
针对当前河道水质资料不健全且难以监测及预警的现状,提出了将神经网络模型运用于河道水质预测分析.运用神经网络模型对河道水质指标实测数据进行优化处理,深入分析水质指标数据,并建立神经网络预测模型.在此基础上,采用归一化和遗传算法两种方法对神经网络模型进行优化,并将优化模型和原神经网络模型分别运用于水质指标数据的预测.结果表明:优化后的神经网络模型可以实现对水质的预测,优化前神经网络模型的预测误差为8.57%,而采用归一化和遗传算法优化后的神经网络模型预测精度分别提高了6.36%和6.73%.同时分析得到了不同水质指标对叶绿素浓度值影响程度按大小依次为氨氮、溶解氧、高锰酸钾指数、pH值、温度.
水质指标;神经网络;归一化;遗传算法
0 前 言
随着全国水质恶化的加剧,水环境管理已经成为解决水资源短缺与水污染加剧的重要措施.水质预测及预警是水环境问题的重要研究内容之一.水质预测的方法一般分为机理建模和数据建模两种方式.机理建模主要通过数学模型建立水质控制方程,从而研究水质的变化规律.随着计算机技术的发展,一些专业的商用软件逐渐运用到水质模拟中[1-4],如荷兰的Delft3D软件中有专门针对水质模拟的WAQ模块,美国环保局推荐使用的WASP水质模型以及丹麦的MIKE11水质模型等.机理建模预测精度较高,但是参数率定复杂,计算时间长.数据建模主要运用统计分析等数学方法,根据已有的水质数据来拟合水质变化的规律或者推测未知条件下水质的变化情况,常见的数据建模方法包括人工神经网络模型、遗传算法、灰色预测等.随着智能算法的优化与普及,数据建模被越来越广泛地运用于水质预测.汪家权等[5]利用RBF神经网络建立了峡山口断面实测水质因子与下游凤台渡口、石头埠两断面水质因子之间的关系,通过峡山口断面的实测数据对下游凤台渡口、石头埠两断面的溶解氧DO、生化需氧量BOD5、高锰酸钾指数进行了预测,指出了神经网络在水质预测中的可行性及合理性.杨晓华等[6]将遗传算法运用于水质模型的参数优选,并指出在求解有关河流横向扩散系数的实际水质模型中,该方法具有更高的精度及更快的收敛效果.
为了实现水质指标数据的分析及预警,本文将神经网络模型运用于水质指标的预测,提出了基于神经网络模型的水质指标实测数据的插补及优化,并结合归一化及遗传算法对模型进行优化,提高了预测精度,较好地实现了水质指标数据的预测,为水质分析提供了新思路.
1 神经网络及遗传算法
1.1神经网络
神经网络模型预测过程是通过对样本的学习来模拟信息之间的内在机制,进而逼近实际系统的动态过程.其主要特性是自学习能力强,适应性好,非线性映射能力强.其中BP神经网络是一种应用最广泛的智能算法,其基本原理如图1所示.
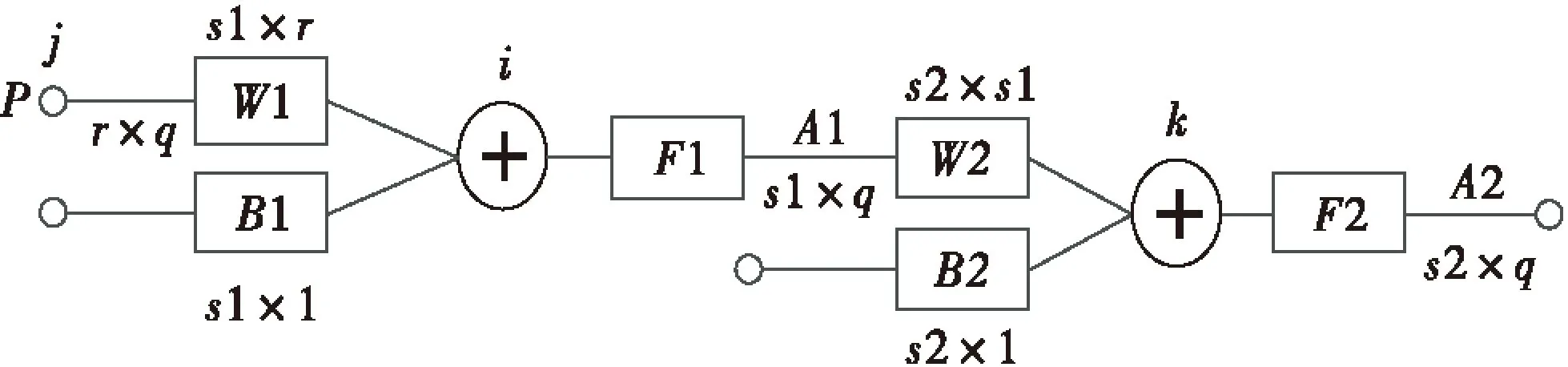
图1 神经网络模型图
如图1,BP神经网络模型拓扑结构包括输入层、一个或者多个隐含层和输出层.输入信息通过输入层经过隐含层输出,如果输出达不到要求的精度,误差信息将反向传播,重新通过输入层输入,通过学习函数不断修正各层神经元的权值与阈值,使得输出结果达到所需要的精度.
BP神经网络模型包括输入输出模型、作用函数模型、误差计算模型和自学习模型.
1)节点输入输出模型
隐含层第i个神经元的输出为:
输出层第k个神经元的输出为:
其中f1、f2分别表示隐含层和输出层的作用函数,ω1ij、ω2ki分别表示隐含层和输出层的神经元的权值,b1i、b2k表示隐含层和输出层的神经元的阈值.pj表示神经网络的输入值,a1i表示神经网络计算的中间值,即隐含层的输出值,a2k表示神经网络的输出值.
2)作用函数模型
作用函数又称激活函数,是一个神经元及网络的核心,网络解决问题的能力与功效除了与网络结构有关外,在很大程度上取决于网络所采用的激活函数.常用的激活函数包括:
①阀值型(硬限制型)
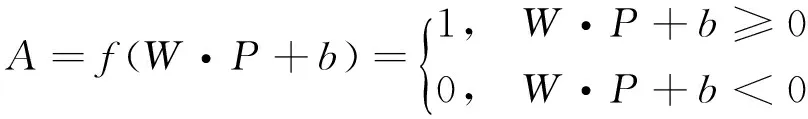
②线性型
A=f(W·P+b)=W·P+b
③S型(Sigmoid)
S型激活函数可以将任意值压缩到(0,1)范围内,常用的有对数S型和双曲S型.
3)误差计算函数
其中tk为目标值.
4)自学习模型
神经网络的学习过程,即连接下层节点和上层节点之间的权重矩阵Wij的设定和误差修正过程.一般采用梯度下降法求权值变化及误差的修正,改进的神经网络的学习算法还包括附加动量法,拟牛顿法,共轭梯度法等.
1.2遗传算法
遗传算法是通过对生物进化机制的模拟来实现全局寻优搜索的目的,现已广泛运用于各种工程中的优化问题[7],其建模过程步骤如下[8]:
1)初始种群生成.在一定范围内产生N个初始数据组,每个数据组即为一个个体,N个数据组为一个种群.
2)种群编码.按照一定的规则将初始种群编码成二进制串,每个二进制串代表一个可能解.
3)适应度评价.根据相应的目标函数,将种群中的每个个体按照一定的适应度评价标准进行评价.
4)遗传选择.根据适应度评价结果,将从当前种群中选择适应度高的个体,使它们进入下一次的迭代,而适应度低的个体被选中的概率较低,甚至被淘汰.
5)交叉过程.将被选中的优良个体通过某种函数作用得到新的个体,新个体将遗传父辈个体的优良特性.
6)变异过程.按一定比例随机选中种群中的某些个体,以一定的概率改变个体的编码值,变异为新个体的产生提供了机会.
重复执行步骤3)~6),随着迭代次数的增加,最终可以得到最适应该问题的个体,即找到了问题的最优解.
2 原始数据优化处理
河道水质指标包括光照,温度,氨氮,溶解氧,高锰酸钾指数,叶绿素浓度等,水质系统具有明显的动态变化随时性、指标数据不完全及不确定性.因此针对水质原始数据存在的误差及不完整性,运用神经网络模型实现原始水质指标实测数据的优化及插补.
某河道为苏北地区重要通航河流,现有2006年及2007年某水质监测站部分水质实测资料(日平均值),水质指标实测数据包括温度、氨氮、溶解氧、高锰酸钾指数、pH值及叶绿素浓度,数据存在部分缺失,缺失数据占全部数据的7.31%.缺失数据的插补及原始数据的优化步骤如下:
1)补充缺失数据.考虑到数据的变化趋势,缺失数据的补充由缺失项前后时间段内数据的插值或拟合得到.本文采用前后时间段内各2个数据,通过拉格朗日插值实现缺失数据的补充.
2)建立神经网络模型.根据水质指标数据之间的相互影响,将温度、氨氮、溶解氧、高锰酸钾指数、pH值及叶绿素浓度中的5个实测指标作为神经网络模型的输入端,将另一个实测值作为神经网络的输出端,从而建立了6个分别用于预测不同水质指标的神经网络模型,并通过模型参数的调整得到最优的神经网络模型如图2所示.
3)将水质指标中的5个数据作为输入端输入神经网络模型得到第6个指标的预测值,并与第6个指标的实测值进行比较,由于实测值存在错误,因此当实测值与预测值误差超过15%时,对实测值进行修改,其中修改的数据不应超过全部数据的15%~20%,否则,原始数据规律性不强或者错误较多,不宜采用神经网络模型预测,取实测值与预测值的平均数作为新的实测值数据,从而得到修正后的6个新的水质指标实测序列.
4)重复2)与3),直到所有数据都能较好的拟合神经网络模型.
采用上述方法对该水质监测站2006年全年及2007年1~3月的水质数据进行优化处理,建立的最优神经网络模型输入端共6个神经元,训练模型目标误差为0.000 05,迭代次数为1 500.通过7次迭代修改,得到最终的优化原始数据.
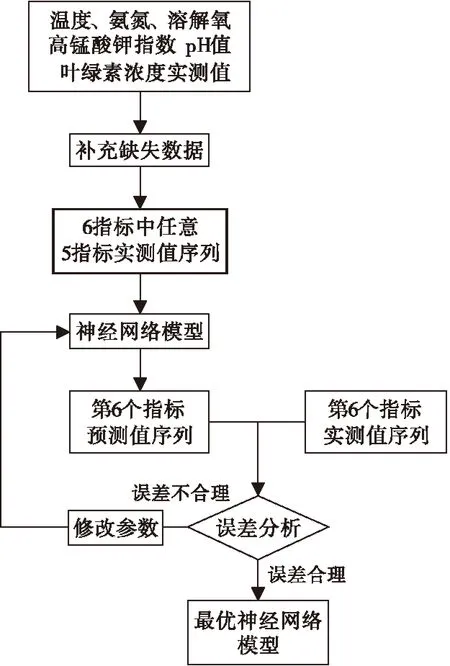
图2 最优神经网络模型流程图
3 水质数据预测分析
3.1基于神经网络模型水质预测
由于实测数据中存在错误及数据缺失等,致使原始数据的关联性较差,通过原始数据的插补及优化,现已得到关联性较好的2006年全年及2007年1~3月某河道水质监测站的优化实测资料,实测水质指标包括温度、氨氮、溶解氧、高锰酸钾指数、pH值以及叶绿素浓度值.本文选取叶绿素浓度值作为预测水质指标,将其余水质指标作为自变量数据输入,如公式(1)所示,从而构建神经网络模型,模型输入端共6个神经元,训练模型目标误差为0.000 05,迭代次数为1500.
(1)
其中,Li,ti,ani,gai,doi,phi分别表示叶绿素浓度和叶绿素浓度值有重要影响的量:温度、氨氮、高锰酸钾指数、溶解氧、pH值.
利用训练后的神经网络模型对2007年4月的该监测站叶绿素浓度进行预测,其中温度、氨氮、溶解氧、高锰酸钾指数及pH值采用实测值,模型预测得到的叶绿素浓度与实测值比较如图3所示.
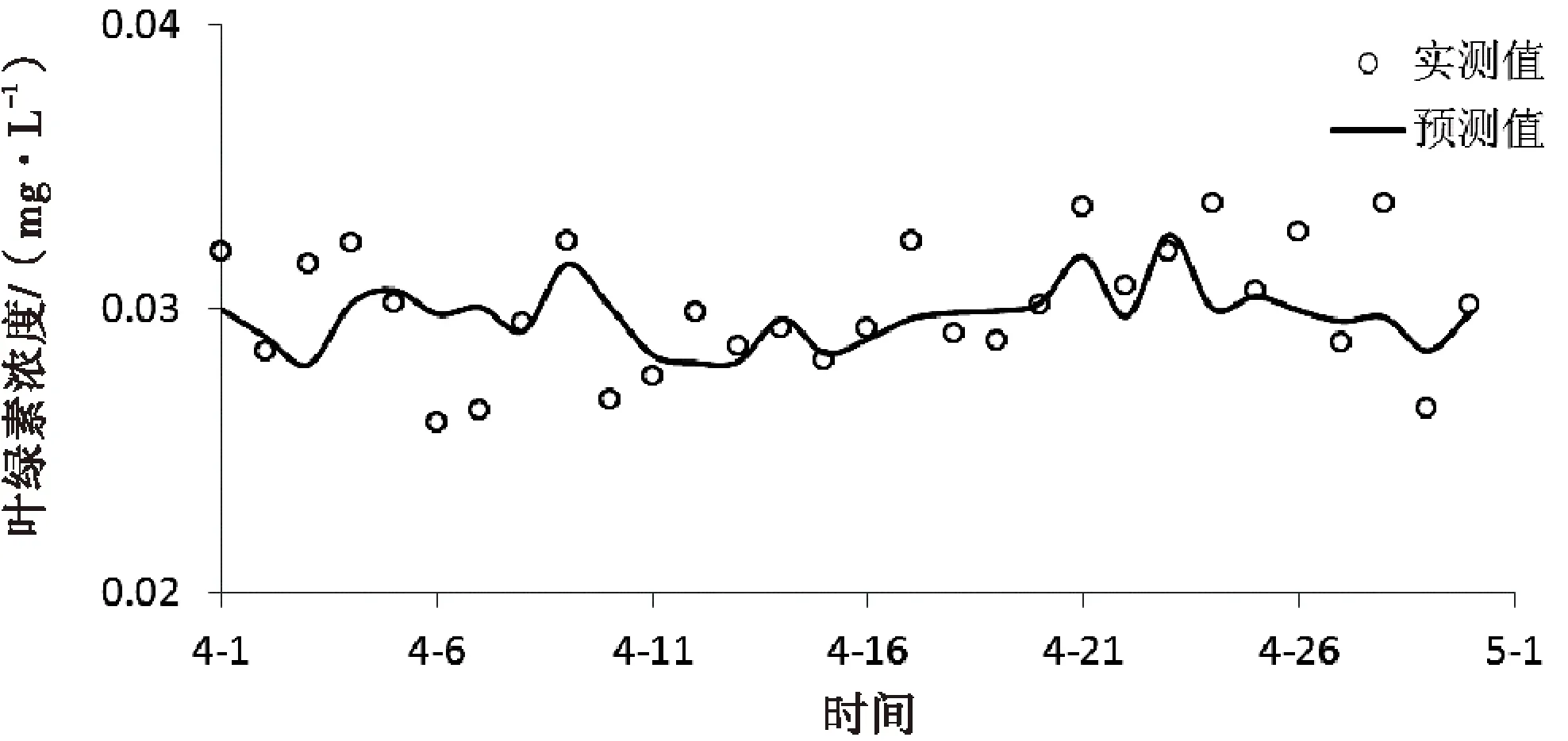
图3 基于神经网络模型的叶绿素浓度预测值与实测值比较
3.2基于优化神经网络模型的水质预测
在上述神经网络模型中,由于水质指标的数据单位不同,各个指标在数值上相差较大,甚至不在一个数量级上,因此直接将数据带入模型计算会产生不可避免的误差,预测精度相对较低.基于此,本文提出了归一化处理和遗传算法两种方法对原始数据进行进一步优化处理,得到优化后的神经网络模型.
1)归一化处理方法
为了避免数据的范围存在较大的差距,采用归一化方法可以有效的减小由于数据本身造成的误差,常用的归一化方法有最大最小值法,均值法,中间值法等,考虑到本文数据的范围及其特点,采用最大最小值法将所有水质数据进行归一化处理,见公式(2),从而使得任何一个水质指标的范围处于[0,1],减小由于数值范围引起的误差,从而建立叶绿素浓度预测模型,见公式(3),并根据公式(4)将模型预测的叶绿素浓度值还原到原数量级.
(2)
其中Xmax,Xmin为某一时间序列内的最大值和最小值.
(3)
(4)
2)基于遗传算法的数据优化
归一化方法虽然消除了数据范围对叶绿素浓度预测的影响,然而事实上,温度、氨氮、溶解氧、高锰酸钾指数及pH值对叶绿素浓度值的影响程度并不相同,归一化的方法等同于将各指标对叶绿素浓度值的影响程度归为相同,这显然与事实不符,将会增大误差.因此,在构建神经网络模型时,考虑模型水质输入值按一定的权重输入神经网络模型,见公式(5).
(5)
其中α1,α2,α3,α4,α5等分别对应叶绿素浓度相应影响因素的权重值,且满足∑αi=1.权重的确定采用遗传算法,其流程图如图4所示.

图4 基于遗传算法的神经网络模型输入值权重确定流程图
首先设定迭代次数、初始种群及数据长度等基本信息.迭代次数视具体情况而定.本文采用迭代100次,初始种群采用30组,每组4个数据,分别表示a1,α2,α3,α4,而α5=1-(α1+α2+α3+α4),同时满足ai∈[0,1].然后将权重与实测值相乘输入神经网络模型训练,适应度函数用训练后的神经网络模型预测值与实测值的平均相对误差表示,遗传算法的交叉率为0.8,变异率为0.005.通过循环往复,最终从30组最优结果中再进行选择,将适应度最大的数据作为最优的权重.
运用优化后的神经网络模型,根据相同时间序列的水质指标对神经网络模型进行训练,模型参数与上文相同,并对同样时间的叶绿素浓度值进行预测,结果如图5所示.
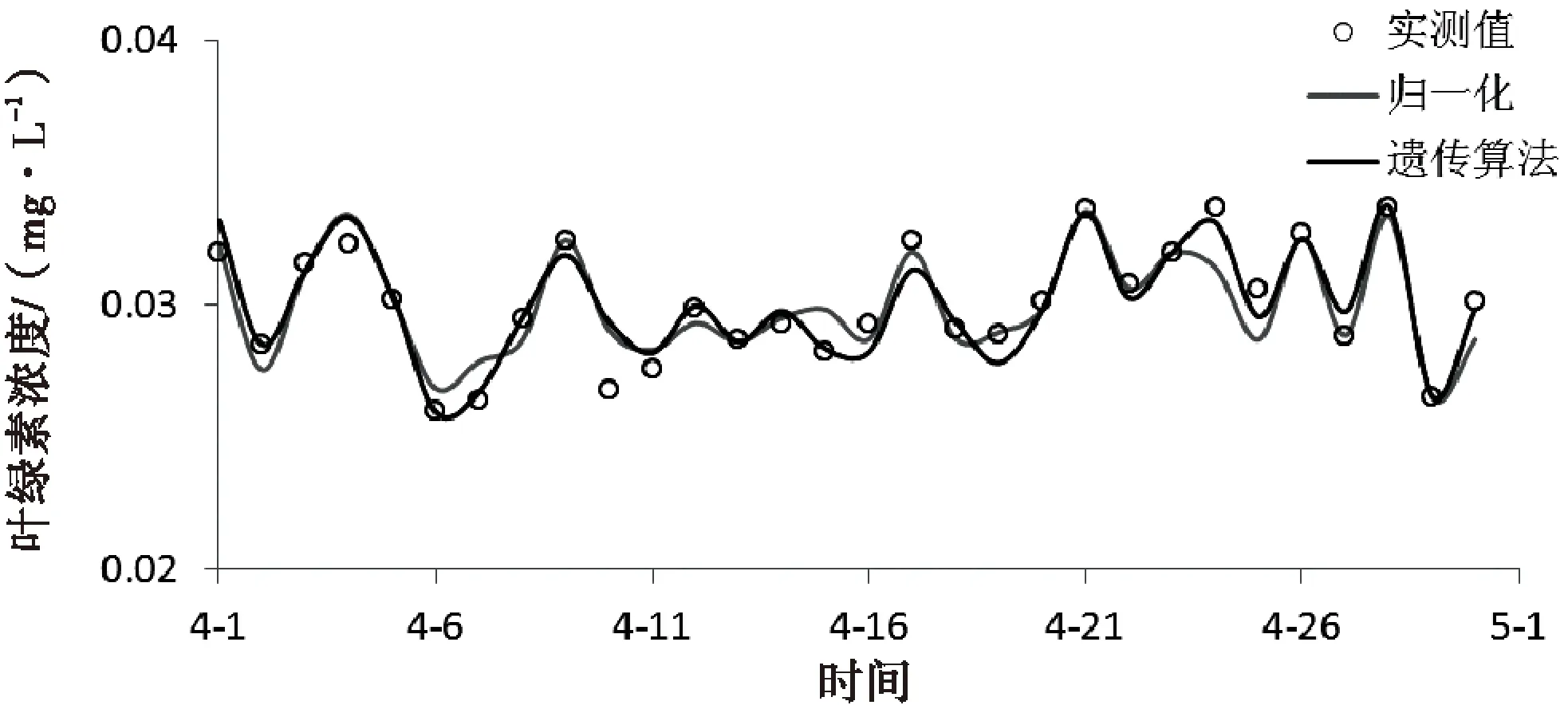
图5 基于优化神经网络模型的叶绿素预测值与实测值比较
3.3预测结果分析
通过比较传统神经网络模型与优化后神经网络模型对叶绿素浓度值的预测,如图3和图5所示,采用优化算法后的神经网络模型对叶绿素浓度的预测精度显著提高,预测结果更加符合实际情况,结果更为精确.同时采用公式(6)计算不同模型预测的平均相对误差,结果见表1.传统的神经网络模型的预测误差为8.57%,而采用归一化和遗传算法后的神经网络模型预测精度分别为2.21%和1.84%.
(6)
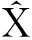

表1 不同优化方法时神经网络模型预测误差
另外,通过遗传算法得到了不同α1,α2,α3,α4,α5的值,该值从一定程度上也反映了温度、氨氮、溶解氧、高锰酸钾指数及pH值对叶绿素浓度影响的程度,见表2, 不同水质指标对叶绿素浓度值影响大小依次为氨氮、溶解氧、高锰酸钾指数、pH值、温度.

表2 不同水质指标权重
由于神经网络模型具有复杂的数学结构,对其内部规律的分析往往需要较高的数学基础.因此,将神经网络模型看做黑箱,通过优化输入数据,也能从一定程度上起到了优化模型的作用.在上述的优化方式中,尽管运用遗传算法优化后的神经网络模型的预测精度比归一化处理的模型精度高0.37%.但是,遗传算法的计算效率远远低于归一化方法.因此,可以根据计算精度及具体情况,适当选择优化输入值的方法,有时候,仅仅只需将原始数据通过扩大10倍或100倍,将数据转化至同一数量级,亦能达到较高的精度要求.
4 结 论
本文通过神经网络模型对水质实测值进行了插补优化,并建立了水质预测的神经网络模型,结合归一化方法和遗传算法对模型进行优化,并运用该模型对某水质监测站的叶绿素浓度值进行了预测,得到如下结论:
1)根据水质指标间的互相影响,建立水质指标预测的神经网络模型可以实现水质指标实测数据的插补及优化.
2)利用优化后的实测水质指标数据建立神经网络模型,并用归一化方法和遗传算法对模型输入数据进行优化,优化后的神经网络模型的预测精度显著提高,传统的神经网络模型的预测误差为8.57%,而采用归一化和遗传算法后的神经网络模型预测精度分别为2.21%和1.84%.
3)通过遗传算法同时得到了不同水质指标对叶绿素浓度值影响按大小依次为:氨氮、溶解氧、高锰酸钾指数、pH值、温度.
[1]李吉学,汪中华.MIKE11在入河排污口设置研究中的应用[A].中国水利学会2010学术年会论文集(上册)[C].2010.
[2]常旭,王黎,李芬,等.MIKE11模型在浑河流域水质预测中的应用[J].水电能源科学,2013(6):58-62.
[3]唐大元.WASP水质模型国内外应用研究进展[J].安徽农业科学,2011(34):21265-21267.
[4]Delft3D_WAQ_User_Manual[M]. 2007:21-22.
[5]于瓅,汪家权.基于RBF神经网络的水质多因素预测[J].中国科技信息,2011(10):56-57.
[6]杨晓华,郦建强.混沌实码遗传算法在水质模型参数优选中的应用[J].水电能源科学,2006(5):1-4.
[7]HongwooL.ComparisonofaGeneralizedPatternSearchAlgorithmandaGeneticAlgorithmintheStructuralOptimizationofGeodesicDome[J].JournaloftheArchitecturalInstituteofKoreaStructure&Construction, 2010, 26(7):3-10.
[8]AkhtarS,HeL.OptimizationandSizingforPropulsionSystemofLiquidRocketUsingGeneticAlgorithm[J].ChineseJournalOfAeronautics, 2007,20(1): 40-46.
[责任编辑王康平]
Application of Optimization Neural Network Model to Water Quality Prediction
Cao Donghua1Chen Jiayuan1Liu Yizhi2Yu Songlin1
(1 .College of Water Conservancy & Hydropower Engineering, Hohai Univ., Nanjing 210098, China; 2.Water Conservancy Bureau of Suqian, Suqian 223800, China)
The paper develops a neural network model to forecast the river water quality in the condition of incomplete and difficult to monitor and early warning rivers. A prediction model of neural network is established based on the optimized and analyzed index data of river water quality. The results are compared with ones by using traditional neural network model. The simulations are more accurate by the optimized neural network model than that by the traditional neural network model. And then the model is applied to predict the water quality. Meanwhile, the effects of different water quality indexes on the chlorophyll concentration are analyzed. Lastly, we find the fact of that the extent of effects from high to low is as follows: ammonia-nitrogen, dissolved oxygen, permanganate index, pH value, temperature.
water quality index;neural network;normalization;genetic algorithm
2016-04-09
曹栋华(1991-),男,硕士研究生,研究方向为水利水电系统规划及工程经济.E-mail: hhusgcdh@163.com
10.13393/j.cnki.issn.1672-948X.2016.04.003
TP183
A
1672-948X(2016)04-0012-05

