溃坝洪水演进影响因素分析

李尚超　牛志伟　刘晓青　吴浩然

(河海大学 水利水电学院， 南京　210098)



溃坝洪水演进影响因素分析

李尚超牛志伟刘晓青吴浩然

(河海大学 水利水电学院， 南京210098)

溃坝洪水往往会对下游人民财产安全造成巨大影响．基于二维浅水方程数学模型，采用两步Taylor-Galerkin有限元方法进行离散，分析溃坝洪水在演进过程中对下游河道的影响因素，结果表明：库容面积、水深比、溃口宽度等因素均对溃坝洪水的水位、传播速度及流量产生影响．库容面积越小，洪峰达到的最高水位值越大；水深比越大，水流流速越大；溃口宽度越大，洪水水位越高，洪峰流量越大．该分析规律为水库大坝安全多因素风险分析提供了参考，为防洪减灾、灾害评估和人民财产安全保护提供了依据．

溃坝；洪水演进；影响因素；风险分析

0　引　言

据统计，1954～2013年，我国共有超过3000座水库发生溃坝；1954～2001年，我国大坝年均溃坝率为8.761×10-4，远远超出世界其他国家．溃坝洪水历时短、速度快、流量大，对下游造成的危害远大于一般洪水危害．影响溃坝洪水演进的因素[1-2]众多，见表1．本文选择库容面积、水深比、溃口尺寸(宽度)作为分析依据．

表1　溃坝洪水影响因素

1　计算原理

1.1控制方程

本文数学模型建立在求解浅水方程的基础上[3]．假设流体是恒温不可压缩的，流体粘性力和加速度的垂直向分量忽略不计，根据纳维-斯托克斯方程，通过对质量守恒方程和动量方程进行水深积分，得到浅水控制方程为

(1)

其中流体力矢量和源矢量分别记为

(2)

(3)

(4)

1.2求解方法

数值求解方法采用有限元两步Taylor-Galerkin算法[3]．此方法不仅在时间和空间上具有二阶精度，而且便于编程，计算速度快，能够有效提高计算效率．

1.3分析方法

各影响因素变化率[1]表示为：

(5)

式中，RX(%)表示某溃坝因素的变化率；Xi表示某溃坝因素的变化值；X0表示某溃坝因素的基本值．

2　数值模型

2.1数值模型验证

本文使用二维矩形局部溃坝模型[3]验证算法．该模型水库尺寸为200m×200m，大坝位于水库中心线，坝体宽10m．初始时刻上下游为静止水位，分别为10m和5m，溃口形状为矩形，溃口宽度75m，如图1所示．计算区域网格为1m×1m的四边形网格．模型验证假定所有边界为固壁边界．

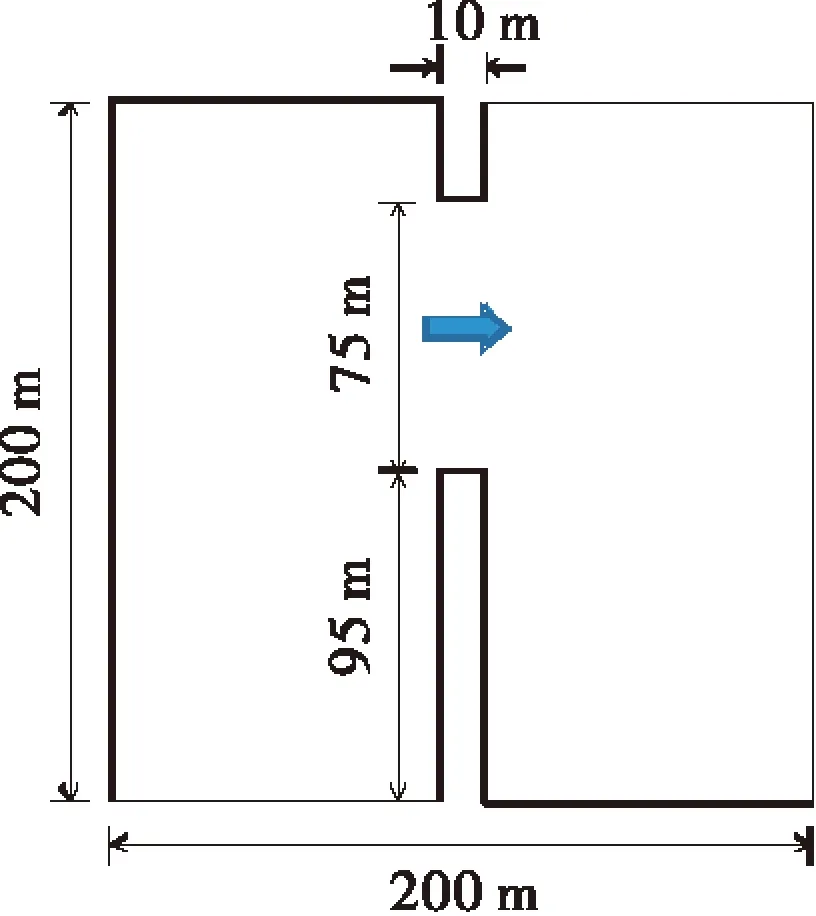
图1　数值验证模型

t=2.15s，t=3.72s，t=5.26s，t=7.32s时刻的水位如图2所示．目前为止，本算例尚无可供参考的理论解，但通过与已有的数值解[4-5]进行比较，本文计算所得数值解与已有数值解较为吻合，证明了本文算法的正确性．

图2　不同时刻水位图

2.2计算分析模型

本文使用的计算分析模型在3.1节模型的基础上，将下游河道长度延长至1km，河道坡降0.1‰，河道糙率0.03，其他参数不变．溃坝计算分析模型如图3所示．

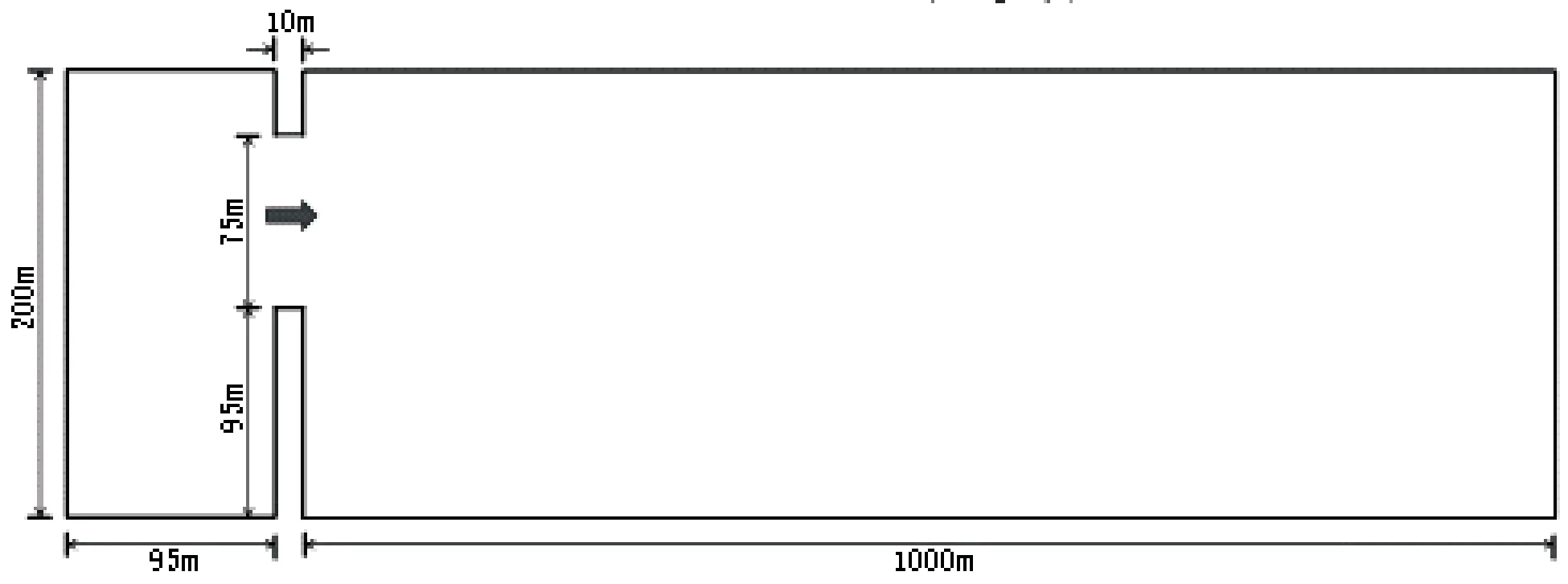
图3　计算分析模型

计算区域网格为四边形网格．计算模型假定出口边界为滑移固壁，其他边界为无滑固壁．

3　影响因素分析

3.1库容面积变化

为了对比库容面积对洪水演进的影响，以库容面积19 000m2为基准值，假设库水量相同，用基准值的±10%、±20%作为变化值，在其他因素不变的前提下应用2.2节模型进行计算分析．即采用5个库水量相同，库容面积分别为15 200m2、17 100m2、19 000m2、20 100m2、22 000m2的计算模型进行分析．初始时刻上下游为静止水位，下游水位为5m；溃口形状为矩形，溃口宽度75m．

不同库容面积情况下，溃坝中心线上、坝址下游5m、100m、1 000m处水位变化曲线如图4所示．溃坝发生后，距离坝址较近下游各处水位骤升达到最高水位；距离坝址较远下游各处，水流先沿河道自由流动，溃坝洪水波传至该处后水位升高；河道各处水位随时间变化逐渐降低，最后趋于稳定．可以看出，库容面积越小溃坝洪水洪峰的最高水位值越大，距离坝址越远的地方洪峰最高水位值越小．库容面积变化对下游各处洪峰流量变化影响如图5所示，距离坝址越近，洪峰流量受库容面积影响越大．

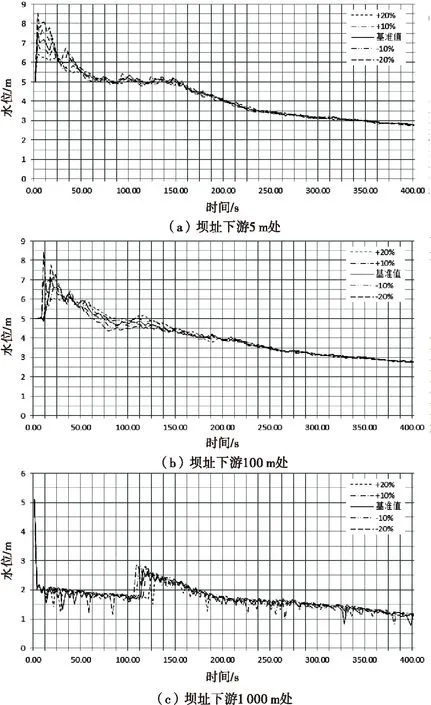
图4　坝址下游各处水位变化曲线

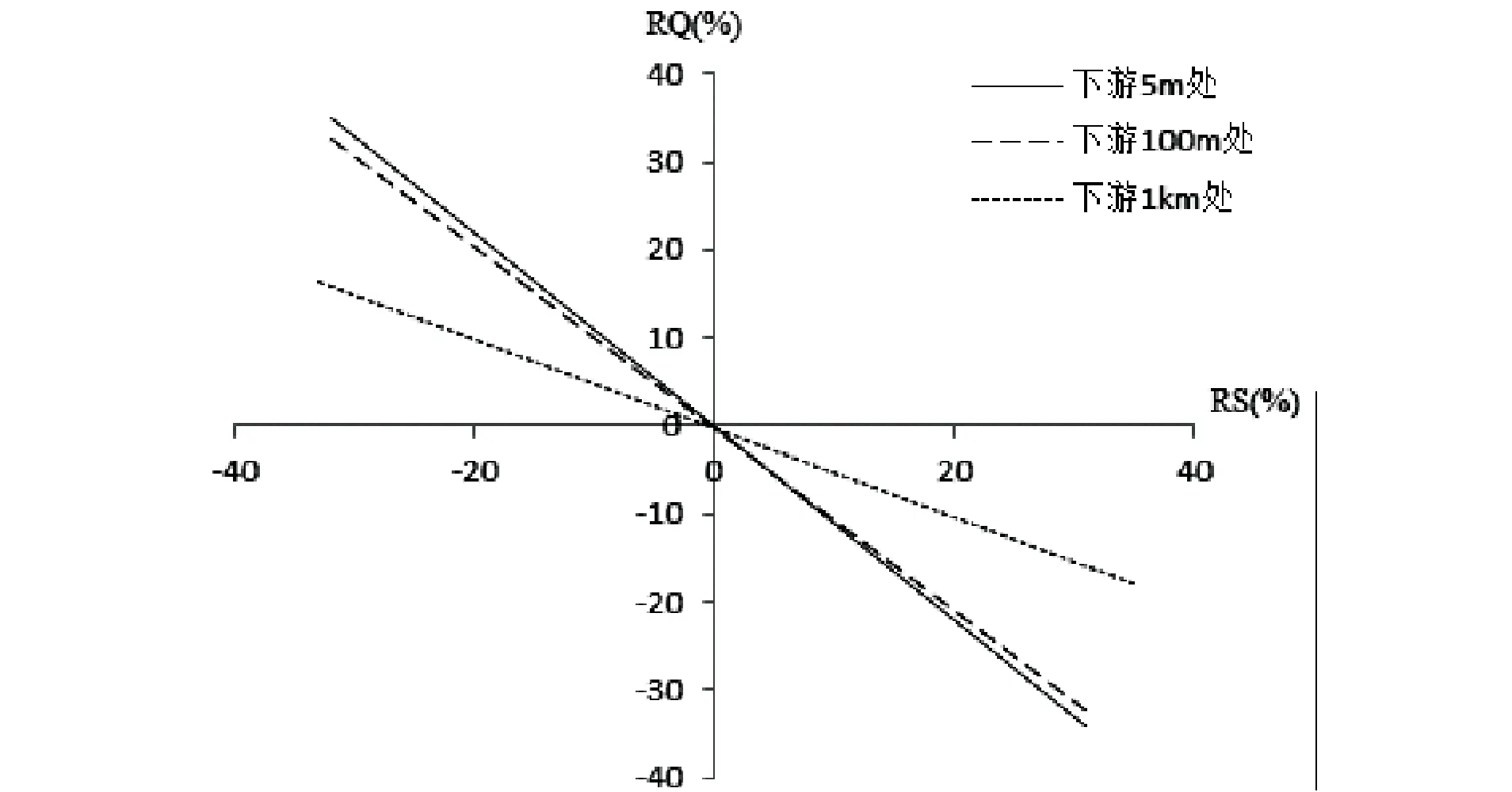
图5　库容面积变化对下游各处洪峰流量变化影响

3.2水深比变化

令水深比=下游水深/上游水深，以水深比0.5为基准值，用基准值的±10%、±20%作为变化值，在其他因素不变的前提下应用模型进行计算分析．即采用5个尺寸相同，水深比分别为0.4、0.45、0.5、0.55、0.6的计算模型进行分析．初始时刻上下游为静止水位，上游水位为10m；溃口形状为矩形，溃口宽度75m．不同水深比情况下，溃坝中心线上、坝址下游5m、100m、1 000m处水位变化曲线如图6所示．

图6　坝址下游各处水位变化曲线

溃坝发生后，距离坝址较近下游各处水位骤升达到最高水位；距离坝址较远下游各处，水流先沿河道自由流动，溃坝洪水波传至该处后水位骤升；不同水深比造成的下游各处水位差异比较明显．

水深比不同时，溃坝洪水波随时间到达下游各处情况如图7所示．可以看出，不同水深比的溃坝洪水波前流速均随时间增大，初始时刻流速基本相同，经过一段时间后，水深比越大水流流速越大．水深比变化对下游各处洪峰流量变化影响如图8所示，可以看出，水深比变化对距离坝址较远处的影响较小．

图7　溃坝洪水演进情况

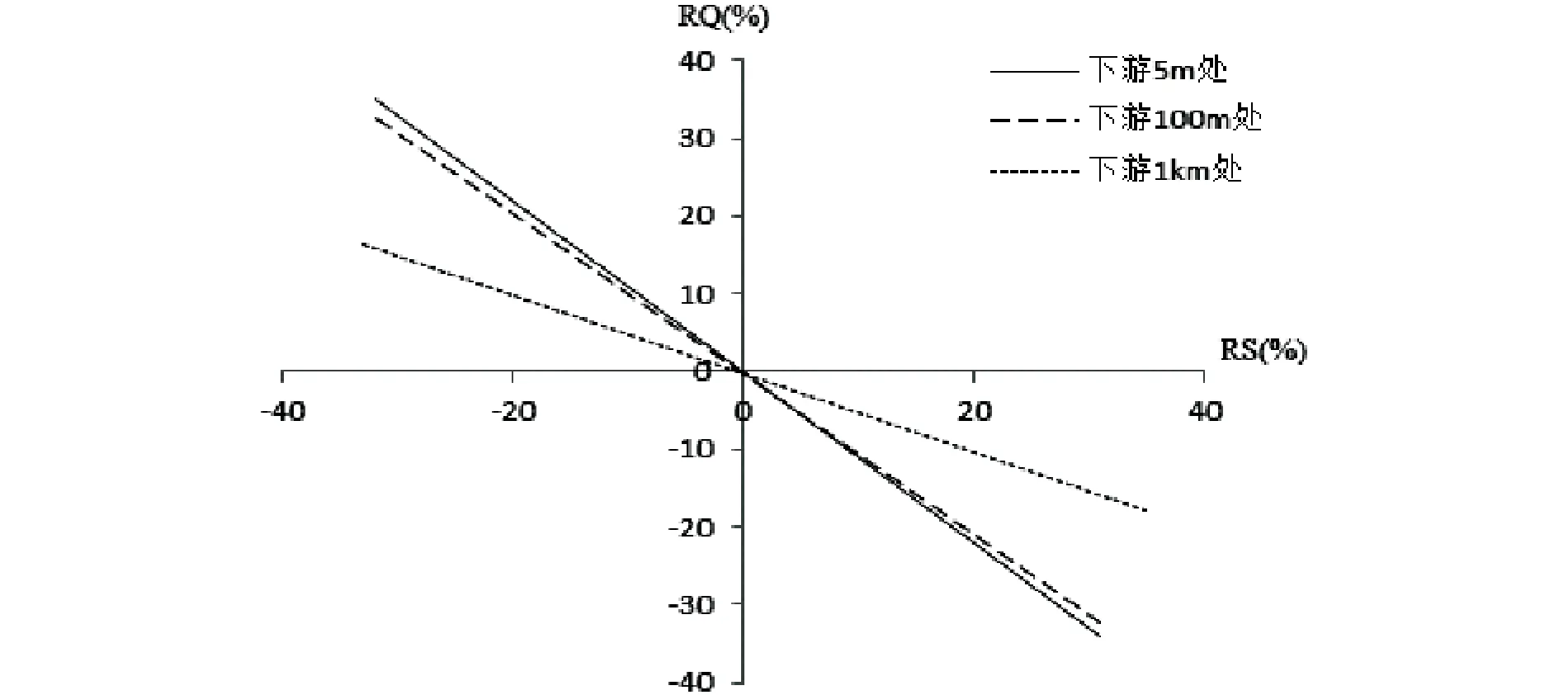
图8　水深比变化对洪峰流量变化影响

3.3溃口宽度变化

为了对比溃口宽度对洪水演进的影响，假设溃口形状为矩形，以溃口宽度75m为基准值，用基准值的±10%、±20%作为变化值，在其他因素不变的前提下应用模型进行计算分析．即5个溃坝模型的溃口宽度分别为91m、83m、75m、67m、59m．初始时刻上下游为静止水位，分别为10m和5m．

溃口宽度变化对下游河道内洪水演进的影响，主要包括流量沿程变化、水深沿程变化两方面，如图9～10所示．溃口宽度对远离坝址处的洪峰流量和洪水水位的影响大于坝址附近处，且溃口宽度越大，洪峰流量越大、洪水水位越高．

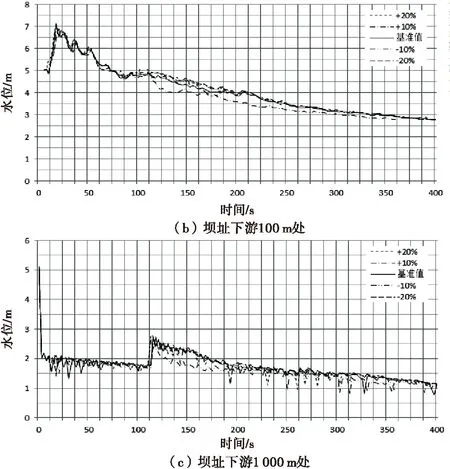
图9　坝址下游各处水位变化曲线

图10　溃口宽度变化对洪峰流量变化影响

4　结　论

本文分析了3种影响溃坝洪水演进的因素，计算结果如图11所示．横坐标分别为库容面积变化率、水深比变化率和溃口宽度变化率，纵坐标为溃坝峰值流量变化率．从变化趋势上看，水深比和溃口宽度引起的变化方向是一致的，库容面积引起的变化方向则相反．从数值上看，坝址下游5m处，3种因素对洪峰流量的影响基本呈线性分布，库容面积每减小10%或水深比每增加10%或溃口宽度每增加10%，都会造成洪峰流量增加10%；坝址下游100m处，库容面积每减小10%或溃口宽度每增加10%，都会造成洪峰流量增加10%，水深比变化引起的洪峰流量变化呈非线性分布且最大不超过20%；坝址下游1 000m处，库容面积每减小20%或溃口宽度每增加10%，都会造成洪峰流量增加10%，水深比变化引起的洪峰流量变化呈非线性分布且最大不超过20%．

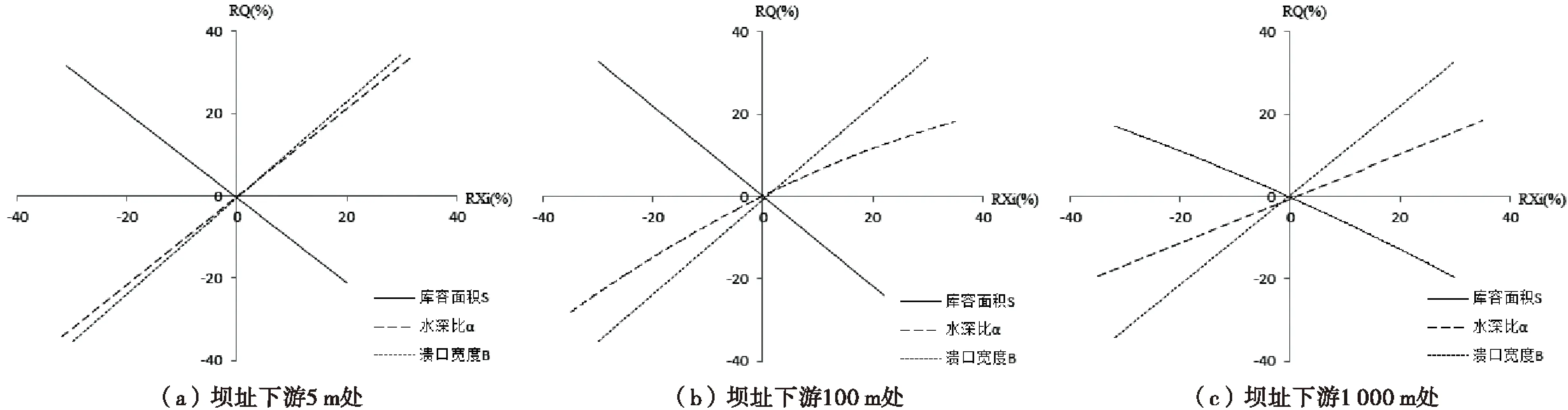
图11　溃坝因素变化对流量的影响

综上，库容面积对下游各处洪水特征的影响与其到坝址距离有关，距离坝址越近，库容面积变化产生的影响越大；水深比在一定程度上对溃坝洪水造成影响，水深比越大，洪水流速越大，洪水水位越高，洪峰流量越大；溃口宽度变化对溃坝洪水的影响显著，溃口宽度越大，下游各处洪水水位越高，洪峰流量越大．3种因素中，溃口宽度对溃坝洪水的影响程度最大．

[1]黄景祥. 溃坝洪水影响因素分析[J]． 华南建设学院西院学报, 1993, 1(1):51-60．

[2]Macdonald T C, Langridge-Monopolis J. Breaching Characteristics of Dam Failures [J]． Journal of Hydraulic Engineering, 1984, 110(5):567-586．

[3]Quecedo M, Pastor M. A Reappraisal of Taylor-Galerkin Algorithm for Drying-Wetting Areas in Shallow Water Computations[J]． International Journal for Numerical Methods in Fluids, 1988, 20(2):153-165．

[4]Zhou J G, Causon D M, Mingham C G, et al. The Surface Gradient Method for the Treatment of Source Terms in the Shallow-Water Equations[J]． Journal of Computational Physics, 2001, 168(1):1-25．

[5]Valerio Caleffi, Alessandro Valiani, Andrea Zanni. Finite Volume Method for Simulating Extreme Flood Events in Natural Channels[J]． Journal of Hydraulic Research, 2003, 41(2):167-177．

[责任编辑王康平]

Analysis of Influencing Factors of Dam-break Flood Routing

Li ShangchaoNiu ZhiweiLiu XiaoqingWu Haoran

(College of Water Conservancy & Hydropower Engineering, Hohai Univ., Nanjing 210098，China)

Dam-break floods always affect the potential for loss of life and damages in the downstream flood plain. A numerical method is used to analyze the influencing factors through numerical simulation method, in which the governing equations are discretized by a fractional finite element method using a two-step Taylor-Galerkin scheme. The results show that three factors, i.e. storage area, water depth ratio of upstream to downstream and dam-break width, affect water level, advancing speed and flow of dam-break floods. If the value of water depth ratio gets greater，the floods of downstream advances faster. The smaller the storage area gets，the higher the flood peak water level becomes. The flood water level and the peak flow increase with the dam-break width. The results provide for reference in analyzing multifactor weighting of dam safety evaluation, as well as in disaster control and reduction, damage assessment, etc.

dam break；flood routing；influencing factor；risk analysis

2016-04-13

水利部公益性行业专项(201301033)；中央高校基本科研业务费专项资金资助(2015B32714)

刘晓青(1965-)，女，教授，研究方向为水工结构工程．E-mail： lxqhhu@163.com

10.13393/j.cnki.issn.1672-948X.2016.04.001

TV122+.4

A

1672-948X(2016)04-0001-05