非线性减震器的多脉冲轨道和同宿树研究*
周莎 张伟† 于天俊
(1.北京工业大学机械工程与应用电子技术学院, 北京 100124)(2.机械结构非线性振动与强度北京市重点实验室, 北京 100124)
非线性减震器的多脉冲轨道和同宿树研究*
周莎1,2张伟1,2†于天俊1,2
(1.北京工业大学机械工程与应用电子技术学院, 北京100124)(2.机械结构非线性振动与强度北京市重点实验室, 北京100124)
针对一类非线性减震器,应用能量相位法研究了减震器系统在1∶0内共振,第一阶主共振情形下系统的多脉冲轨道和同宿树. 首先, 将系统的无量纲动力学控制方程转化为近可积哈密顿系统的标准形式.其次,研究了该系统的未扰动力学行为和扰动动力学行为, 分析了耗散因子及相位漂移角对多脉冲轨道脉冲数和层半径的影响, 揭示了这类非线性减震器能量从高频模态向低频模态转移的动力学机理.
非线性减震器,能量相位法,多脉冲轨道,同宿树,能量转移
引言
航天器的发射阶段虽然只有短短的几十分钟,却承受着在整个寿命周期内最为严酷的动力学环境. 有效载荷受到的环境载荷包含几十赫兹, 几百到上千赫兹的低、中、高频的振动与冲击. 近年来, 由卫星活动部件引起的微振动对敏感载荷性能的影响也引起了国内外学者的关注. 微振动的主要特点是幅值小、频带宽、控制难[1]. 于是, 航天器隔振与减震技术应运而生. 通过研究航天器减震/隔振和阻尼技术对航天器动力学特性的影响, 以改善航天器的振动环境和航天器及部件动力学特性[2].
能量相位法[3-7]最早由Haller提出, 是一种分析高维非线性系统多脉冲混沌运动的全局摄动方法. Yao[8]利用能量相位法研究了非线性非平面运动悬臂梁的多脉冲混沌动力学, Yu[9]利用能量相位法研究了两自由度旋转圆盘的多脉冲同宿轨道和同宿分岔树. Li[10]应用随机Melnikov理论确定了移动载荷弹性梁系统在均方意义下发生异宿分岔以及混沌的边界条件.
本文应用能量相位法研究了非线性减震器系统在1∶0内共振, 第一阶主共振情形下系统的多脉冲轨道和同宿树.
1 非线性减震器模型
两个自由度非线性减震器模型如图1. 非线性减震器由质量为m、惯性矩为Λ的刚体, 连着两个相同的弹簧阻尼系统组成. 假设阻尼系统的线性粘弹性阻尼系数为β, 弹簧是非线性的且弹性势能为
(1)
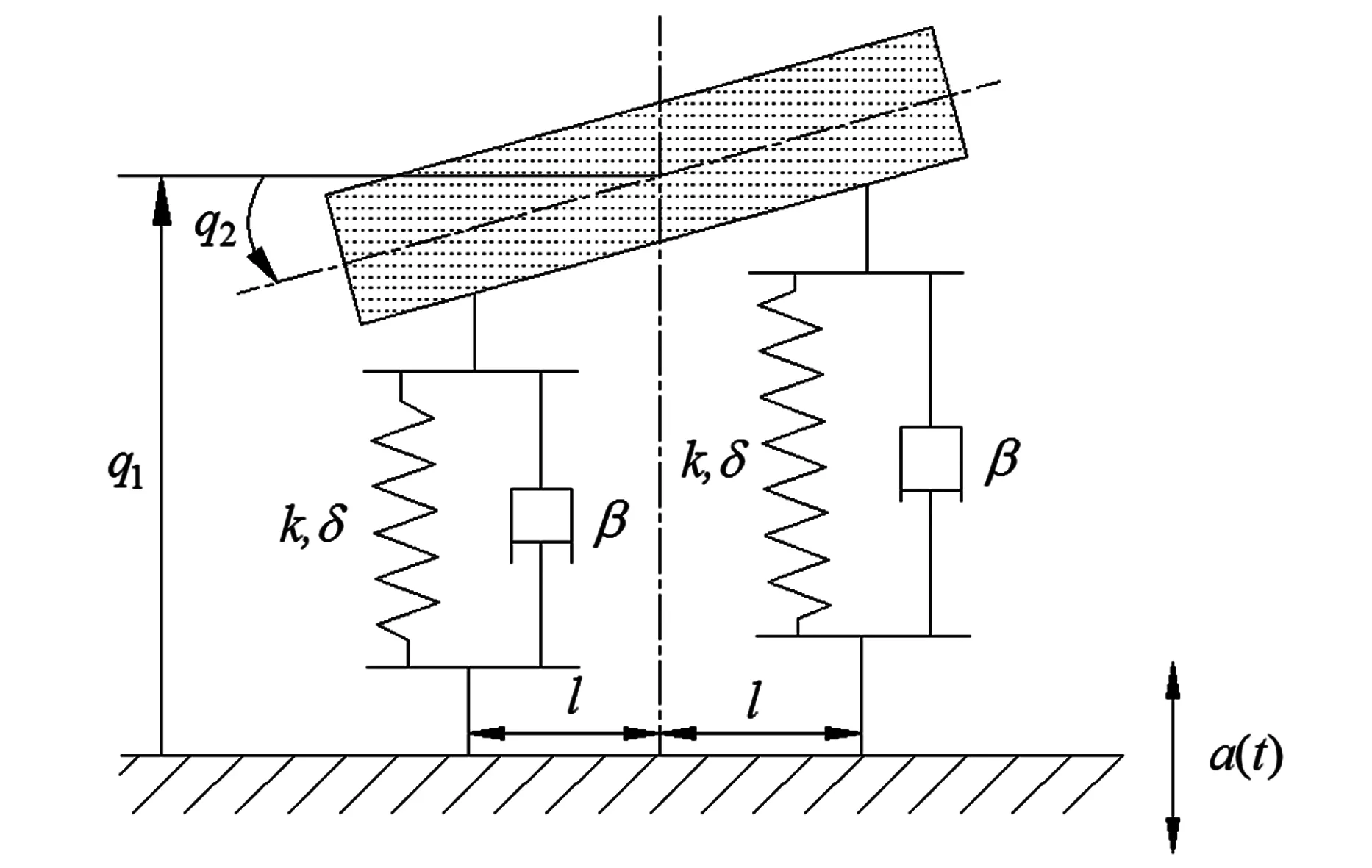
图1 非线性减震器模型Fig. 1 The model of nonlinear vibration absorber
假设系统受到垂直方向的激励a(t)=Asinνt,l表示对称垂直轴到每一个弹簧阻尼系统接触点的距离,q1和q2分别表示垂直方向上相对位移和相对仰角. 非线性减震器的无量纲控制方程为
(2a)
为了应用能量相位法, 需将方程(2)转化为近可积哈密顿系统的标准形式. 本文考虑惯性矩Λ足够大, 使得两阶模态的固有频率之比接近1∶0, 即(ω0/r)2=0+εσ, 其中σ为调谐参数; 外共振满足ν=ω0(1-ελ). 应用规范形理论可将方程(2)转化为如下近可积哈密顿系统的形式
(3a)
(3b)
(3c)
(3d)
其中哈密顿函数
(4a)
(4b)
耗散项
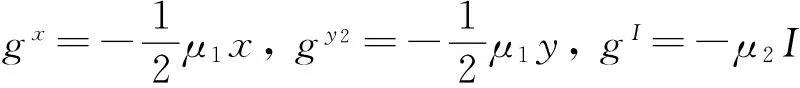
gθ=0
(4c)
2 能量相位法
2.1未扰动系统动力学

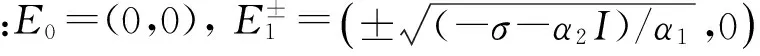
令k=-σ-α2I, 由未扰动哈密顿函数H0(x,y)=H0(0,0)可求得过鞍点E0的同宿轨道为
(5a)

(5b)
此时, 未扰动系统存在二维法向双曲不变流形
(6)
事实上, 流形M0上包含的是系统(2)的第一阶, 即高频模态的运动.
限制在不变流形M0上的动力学方程为

(7a)
(7b)
当(1+λ)ω0+α3I=0,即I=Ir=-(1+λ)ω0/α3时, (I,θ)平面在不变流形M0上是不动点圆. 连接不动点圆上任意两点的异宿轨道的相位差
Δθ=θ(+,Ir)-θ(-,
(8)
2.2扰动系统动力学
根据法向双曲不变流形在小扰动下不变流形的保持性, 对于充分小的ε>0, 法向双曲不变流形扰动为

(9)
为了研究共振区的动力学行为, 引入如下变换
(10)
限制在流形Mε上的动力学方程为
(11a)
(11b)
ε=0时方程(11)对应的哈密顿函数为
(12)
且存在不动点
(13a)
(13b)
耗散扰动下鞍点P0扰动后仍为鞍点Pε, 中心Q0扰动后为稳定的焦点Qε.
能量差分函数
cosθ]+nμ2M
(14)
其中

引入耗散因子d=μ2/F, 能量差分函数在区间θ∈[0,2π]上存在横截零点
(15a)
(15b)
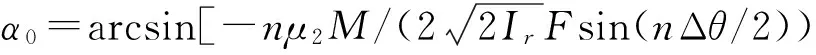
定义能量序列
h0=HD(0,θs),

集序列
A0=φ,
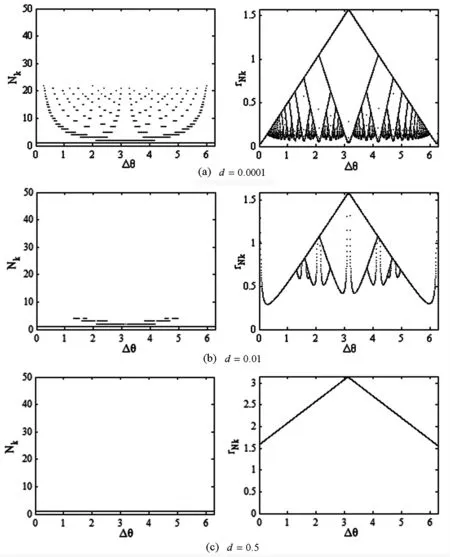
An={(h,θ)|HD(h,θ) 脉冲序列 N1=1, Nk=min{n∈Z|n>Nk-1,hn>hNk-1},k≥2. 层序列 LNk=Int(ANkANk-1). 层半径序列 图2给出了哈密顿扰动(无阻尼)下, 系统的脉冲数Nk与层半径rNk在区间Δθ∈[0,2π]上的分布情形. 图2(a)是哈密顿扰动下脉冲数的分布情形, 在每个N值处的水平线表明这个水平线所在的Δθ区间上, 总存在着无穷个N脉冲轨道. 图2(b)是层半径的同宿树, 即层半径随着分岔参数Δθ的变化而变化的情形, 该图是无穷的二叉树, 也称之为“同宿树”; 同宿树的结点对应层序列的分岔. 图2 哈密顿扰动下脉冲数和层半径的分布情形(a)脉冲数的分布情形 (b)层半径的同宿树Fig. 2 Distribution of pulse number and layer radii under Hamiltonian perturbation(a) Distribution of pulse numbe (b) Homoclinic tree of layer radii 图3给出了脉冲数Nk与层半径rNk分别在耗散因子d=0.0001、d=0.01、d=0.5时的分布情形.随着耗散因子的不断增大, 最大脉冲数逐渐减小,同宿树逐渐破裂. 图3 脉冲图和层半径在不同耗散因子下的分布情形 Fig. 3 Distribution of pulse number and layer radiiin different dissipative factor 本文采用能量相位法研究了非线性减震器在1∶0内共振, 第一阶主共振情形下系统的多脉冲轨道和同宿树. 通过引入能量序列、脉冲序列, 分析了相位漂移角及耗散因子对多脉冲轨道脉冲数和层半径的影响. 在哈密顿扰动下, 同宿于慢流形的同宿轨总是存在. 在耗散扰动下, 随着耗散因子的不断增大,多脉冲轨道的脉冲数逐渐减小, 同宿树逐渐破裂, 揭示了能量从高频模态向低频模态转移的动力学机理. 1孟光,周徐斌. 卫星微振动及控制技术进展. 航空学报, 2015,36(8):2609~2619 (Meng G, Zhou X B. Progress review of satellite micro-vibration and control.ActaAeronauticaetAstronauticaSinica, 2015, 38(8): 2609~2619(in Chinese)) 2黄文虎,曹登庆,韩增尧. 航天器动力学与控制的研究进展与展望. 力学进展, 2012,42(4):367~394 (Huang W H, Cao D Q, Han Z Y. Advances and trends in dynamics and control of spacecrafts.AdvancesinMechanics, 2012,42(4):367~394 (in Chinese)) 3Haller G, Wiggins S. Orbits homoclinic to resonances: the Hamiltonian case.PhysicaD, 1993,66(3-4):298~346 4Haller G, Wiggins S. Geometry and chaos near resonant equilibria of 3-DOF Hamiltonian system.PhysicaD, 1996,90(4):319~365 5Haller G. Universal homoclinic bifurcations and chaos near double resonances.JournalofStatisticalPhysics, 1997,86(5):1011~1051 6Haller G, Wiggins S. N-pulse homoclinic orbits in pertur-bations of resonant Hamiltonian systems.ArchiveforRationalMechanicsandAnalysis, 1995,130(1):25~101 7Haller G. Chaos near resonances. New York: Springer-Verlag, 1999 8Yao M H, Zhang W. Multi-pulse shilnikov orbits and chaotic dynamics in nonlinear nonplanar motion of a cantilever beam.InternationalJournalofBifurcationandChaos, 2005,15(15):3923~3952 9Yu W Q, Chen F Q. Orbits homoclinic to resonances in a harmonicaly excited and undamed circular plate.Meccanica, 2010,45:567~575 10李海涛,秦卫阳,田瑞兰. 随机及移动载荷激励下弹性梁分岔与混沌. 动力学与控制学报, 2015,13(6):417~422 (Li H T, Qin W Y, Tian R L. Bifurcation and chaos of beam subjected to moving loads and random excitations.JournalofDynamicsandControl, 2015,13(6):417~422 (in Chinese)) *The project supported by the National Natural Science Foundation of China(11290152,11322214). † Corresponding author E-mail: sandyzhang0@yahoo.com 02 December 2015, revised 29 December 2015. MULTI-PULSE ORBITS AND HOMOCLINIC TREES OF NONLINEAR VIBRATION ABSORBER* Zhou ShaZhang Wei†Yu Tian-jun (BeijingKeyLaboratoryofNonlinearVibrationsandStrengthofMechanicalStructures,CollegeofMechanicalEngineering,BeijingUniversityofTechnology,Beijing100124,China) In this paper, the energy phase method is applied to analysis the multi-pulse orbits and homoclinic trees of the nonlinear vibration absorber model under 1∶0 internal resonance and the first order primary resonance. Firstly, the nonlinear governing equations are transformed to the standard form of near-integrable Hamiltonian systems. Moreover, the unperturbed dynamics and perturbed dynamics are examined. The influence of dissipative factor and the phase shift on the pulse number and layer radii of the multi-pulse orbits of system are analyzed. The results show that energy is transferred from the high-frequency mode to the low-frequency mode in these systems. nonlinear vibration absorber,energy phase method,multi-pulse orbits,homoclinic trees,energy transfer E-mail: sandyzhang0@yahoo.com 10.6052/1672-6553-2016-16 2015-12-02收到第1稿, 2015-12-29收到修改稿. *国家自然科学基金资助项目(11290152,11322214)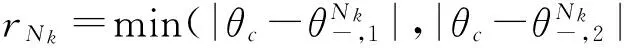

4 小结

