公路桥梁动力冲击系数研究进展*

邓露　王维

(1.湖南大学风工程与桥梁工程湖南省重点实验室, 长沙　410082) (2.湖南大学土木工程学院, 长沙　410082)



公路桥梁动力冲击系数研究进展*

邓露1,2†王维2

(1.湖南大学风工程与桥梁工程湖南省重点实验室, 长沙410082) (2.湖南大学土木工程学院, 长沙410082)

对近20年来国内外在公路桥梁动力冲击系数方面的研究进展进行了回顾.首先介绍了动力冲击系数的概念.然后,分别从试验研究和数值模拟两方面介绍了相关的研究进展和成果,并详细讨论了不同参数对动力冲击系数的影响.接着,介绍了世界各国规范中动力冲击系数的取值规定.最后,总结了该领域已取得的一些重要进展,并探讨了该课题可以进一步研究的方向.

车桥耦合作用,动力冲击系数,现场试验,数值模拟

引言

移动车辆荷载引起的桥梁振动一直是桥梁界关注的重要问题之一.由于路面不平整等因素的影响,行驶的车辆会对桥梁产生动力冲击效应,增大桥梁的响应.桥梁设计中这种冲击效应通常用动力冲击系数(IM)来表征.IM是桥梁设计和评估中的重要参数.然而,车辆和桥梁的相互作用机理非常复杂,准确地评估动力冲击系数并非易事.很多学者研究了车辆荷载作用下桥梁的动力响应,然而在该问题的一些认识上尚未达成共识.Paultre[1]总结了1992年以前关于桥梁动力学和动力冲击效应评估的研究.McLean和Marsh[2]总结了车辆动力效应对公路桥梁影响的重要理论和研究成果.李小珍[3]回顾了公路车桥耦合振动早期的实验研究和经典分析理论, 并归纳总结了公路车桥耦合振动研究中关于车桥分析模型、路面不平整度及数值计算方法等几个方面的主要成果.近年来,有限元和计算技术的发展促进了复杂三维车桥模型在该研究领域中的应用,大大提高了桥梁动力响应的计算效率和精度.

世界各国的桥梁规范对IM给出了不同的取值.例如美国先前的AASHTO桥梁设计规范[4]曾经定义IM为桥跨长的函数,而现版AASHTO规范[5]则采用0.33的恒值.加拿大现版规范[6]则根据车辆轴数来确定IM.而我国目前的桥梁规范[7]则把IM定义为桥梁基频的函数.尽管采用了不同的表达方式和取值,研究表明[8-10]桥梁规范很多情况下并不能准确地描述实际的IM,原因在于简单的取值和表达方式并不能全面反映各个重要参数对冲击系数的影响.

本文旨在回顾最近20年来在公路桥梁动力冲击系数方面的研究进展.文章首先介绍了动力冲击系数的概念,并从试验设备、流程和数据处理方法等方面介绍了冲击系数的试验研究.然后,从数值模型和分析方法两方面介绍了冲击系数的数值研究,并详细讨论了不同参数对冲击系数的影响.接着,介绍了世界各国规范中冲击系数的取值规定.最后,基于动力冲击系数的研究现状总结了一些有意义的结论,并探讨了该课题可以进一步研究的方向.

1　动力冲击系数的定义

目前常用的动力冲击系数的定义如式(1)所示,其表示在动态车辆荷载作用下的桥梁静态响应的增量比.

(1)

式(1)中Rdyn和Rsta分别表示桥梁上目标位置的最大动、静响应.然而,动力放大系数 (DAF)也被用来表征动力冲击效应的大小,其值为最大动、静响应的比值.因此,这两个定义的关系为:IM=DAF-1.计算IM时最大动响应通常取测量或计算的响应最大值,而最大静响应可通过准静态试验、滤波法或有限元计算获得[1].

根据不同的桥梁响应计算的IM值并不相等.有些研究表明根据位移计算的IM比根据应变计算的值大[11-13],而有些研究则得到相反的结论[14-15].一些学者指出工程实践中利用位移计算的IM进行内力设计是不合理的[14,16].然而,这种现象在规范和工程实践中并没有明确区分.

此外,Caprani[17]提出了评估动力系数的概念.该概念类似于动力放大系数,其定义为特征动荷载效应与特征静荷载响应的比值.特征动/静荷载效应是指在指定重现期内不同荷载条件下的最大动/静响应值.与传统偏于保守的动力放大系数相比,评估动力系数是一种基于外推法计算桥梁全寿命周期内IM的统计方法.O′Brien发现评估动力系数比IM小得多[18],表明用IM评估现役桥梁可能过于保守.

2　IM的现场试验研究

现场试验是研究车辆荷载作用下桥梁动力响应最直接最可信的方法.从19世纪50年代到80年代,美国、加拿大、瑞士等许多国家进行了大规模的桥梁现场试验,积累了许多冲击系数的原始试验数据,为各国规范中冲击系数的取值规定提供了依据.Paultre[1]以及McLean 和 Marsh[2]对这些试验进行了详细的介绍.

2.1测试流程

现场试验需获得桥梁测量点的动/静响应来计算冲击系数.在静载试验中,先根据桥梁的影响线确定测量点最大静响应对应的最不利加载线路和位置[19],然后让试验车辆按指定线路以非常缓慢的速度通过桥梁或让试验车辆直接停放在预先确定的最不利加载位置上获得测量点的最大静响应.在动力荷载试验中,试验车辆以预定的速度通过预先确定的最不利加载线路.测量点的最大动响应则可从响应时程曲线中获得.

2.2设备及数据获取

获取准确的桥梁响应在现场试验中至关重要.根据不同试验目的和目标响应,常用的试验元器件有位移传感器、应变计、加速度计等.加速度计主要用来获取桥梁振动的频率和振型[20-21],位移传感器和应变计则用来测量桥梁的位移和应变响应.元器件的安装位置也是一个重要考虑的因素,可借助有限元分析进行优化.此外,一般需要把沿桥梁横向安装的元器件安装在荷载影响区域以内以获得较大的桥梁响应,从而避免获得过大的不切实际的IM[1,22].

数据采集系统通常用来收集和分析数据.为了避免数据混乱,数据采样频率至少应是测量点最大目标振动频率的2倍[1].有些现场试验的采样频率是测量点预期振动频率的10倍以上[23],有些甚至是基频的40～50倍[24].

2.3数据处理

通过静载试验获取桥梁测量点的静载响应会遇到两个方面的困难:一是很难控制静/动载试验时车辆的行驶路线完全相同；二是由于交通通行的需求,在桥梁上实施静载试验一般不易.滤波技术使得从测量点的动力响应中提取其静力响应成为可能.低通数字滤波器目前被广泛使用[25-26],其滤波频率的设置标准是要剔除动态响应但保持静态响应的完整.为达到这一目标,其频率范围需覆盖车辆静力作用下引起的桥梁响应的频率范围.合理设定滤波器的滤波级数非常重要.在保持频率不变的情况下,滤波级数的增加通常会使滤波效果更好[27].现场试验数据常用十级滤波器处理[22-23].

然而,滤波技术也有一定的缺陷.当车辆的竖向振动频率低于滤波器频率的最小值时,获得的桥梁静态响应可能偏大从而低估IM.通常车辆的竖向振动频率在2至5Hz之间[20,28],所以滤波器的频率需避开这个频率范围.另外,对于长度小于15m的短桥,车速和桥长的比值可能非常接近或大于桥梁的基频[1].这种情况下,除非动态响应明显被高阶模态控制,否则通过滤波法不能得到完整的桥梁静态响应从而可能导致不准确的IM.

3　IM的数值分析研究

尽管现场试验是研究车辆荷载作用下桥梁动力响应最可靠的方法,但是,现场试验具有成本高和不便利等缺点,而数值方法能有效地克服这些缺点.尤其是随着计算机技术的快速发展和大型商业有限元软件的出现,复杂的三维桥梁和车辆模型被应用到研究中,并且模拟结果与试验结果取得了良好的吻合.

3.1桥梁模型

早期的车桥耦合振动研究中,常用一维的梁单元模拟桥梁的上部结构,这种简化不能准确反映桥梁的空间响应.后来,随着理论的发展及有限元的应用,更复杂的桥梁模型得到了应用,包括二维的平面模型[18,29]、梁格模型[8,26,30]和三维实体有限元模型[10,31]等.González[32]详细介绍了桥梁的各种模型.

3.2路面不平整度模型

路面不平整是引起车桥振动的主要激励,准确地描述路面不平整度对研究车桥的相互作用非常重要.路面不平整度通常被看作为均值为零的静态高斯随机过程,其表达式可根据功率谱密度函数通过傅里叶逆变换得到[33-34].路面不平整度的表达式为:

(2)

式中θk表示从0到2π均匀分布的随机相位角；φ()表示路面不平整度功率谱函数(m3/cycle/m)；nk表示波的个数(cycle/m).

ISO-8608[35]规定的功率谱函数表达式如下:

(3)

式中n表示空间频率；n0表示1/2π的间断频率(cycle/m);φ(n0)表示路面不平整系数,与路面状况有关；n1和n2分别表示截止频率的上下限.ISO-8608中不同路面不平整度等级对应的不平整度系数的范围如表1所示.

在大多数数值研究中,路面不平整度的横向差异性通常没有被考虑,这与实际的路面情况有一定的差别,也会导致车辆的转动行为不被激发出来.为此,一些学者建立了更符合实际情况的二维路面不平整度模型.Oliva[36]开发了一种能有效生成一对平行路面不平整度的方法.他们发现忽略路面不平整度的横向差异性将高估IM. Liu[37]通过随机关联方法模拟了桥梁的横向路面不平整度,发现横向不平整度关联性越好导致的IM越大,不考虑路面横向差异性(完全关联时)得到的IM偏于保守但仍能被工程实践所接受.此外,考虑到长期重复的车辆荷载作用会导致路面不断恶化这一现象,有些学者还提出了路面不平整度随时间的退化模型[38].

3.3车辆模型

车辆模型经历了从简单到复杂的发展历程,一般可分为三类:只有一或两个自由度的一维弹簧质子模型[11,39]、多轴平面车辆模型[40-41]和三维车辆模型[18,42].其中,三维牵引式挂车模型被广泛用来模拟卡车.在三维车辆模型中,车体通常用一个具有竖向运动、俯仰运动和转动3个自由度的刚体质量表示,每个车轮用一个具有竖向自由度的集中质量表示,牵引车和拖车通过铰接点连接[43-44].一个典型的11自由度3轴车辆模型如图1所示.另外,Kwasniewski[31]建立了一个有限元卡车模型.该模型有三维的悬挂系统、气动系统和滚动车轮,其动力特性的准确性得到了试验验证.

图1　三维车辆模型Fig. 1　Three-dimensional vehicle model

3.4交通流模型

单个车辆过桥时产生的动力效应往往不能很好地代表实际情况下交通荷载对桥梁的冲击效应,因此需要对随机交通流作用下的冲击系数进行研究.通过实测方法来长期监测桥梁上的交通流有诸多不便,许多学者采用蒙特卡洛法对交通流进行模拟[45-46].该方法先通过分析一定时期内的监测车流数据获得车重、车速、轴重、轴间距、车头距等交通流特征参数的统计分布特性,然后通过蒙特卡洛方法生成一定时期内的交通流.利用生成的交通流,通过数值模拟计算得到这段时期内的桥梁响应极值的集合,而更长目标时期内的极值响应则可通过极值理论外推得到.

3.5车桥耦合方程的求解

车桥相互作用中,车辆运动方程可表示为:

(4)

式中[Mv], [Cv]和[Kv]分别表示车辆的质量矩阵、阻尼矩阵和刚度矩阵；{dv}表示车辆的位移向量；{FG}表示车辆所受重力荷载向量；{Fv}表示桥面对车辆的作用力向量.桥梁的运动方程可表示为:

(5)

式中[Mb], [Cb]和[Kb]分别表示桥梁的质量矩阵、阻尼矩阵和刚度矩阵；{db}表示桥梁的位移向量；{Fb}表示车辆作用在桥面的作用力向量.

根据车桥接触点的位移关系和接触力关系,可以建立如下的车桥耦合方程:

(6)

式中Cb-b,Cb-v,Cv-b,Kb-b,Kb-v,Kv-b,Fb-r和Fv-r表示由于车桥相互作用引起的阻尼、刚度和作用力项.

求解车桥耦合振动方程的方法通常可以分为两类:迭代法[40,43,47]和耦合式解法[10,47].迭代法中车辆和桥梁的振动方程在满足车桥接触点位移协调和力平衡的条件下分别迭代求解.该方法的计算结果精度高但计算量很大.耦合式解法把车辆和桥梁振动方程组合成一个耦合方程,通常用Newmark法[14,48]或龙格库塔法求解[1,49].该法能有效地减小耦合方程未知数的个数, 大幅减少计算量,在求解车桥耦合振动问题中经常被应用.模态叠加法也通常被用到求解桥梁动力方程的过程中,可以大大减小计算量.通常取前20阶模态来计算桥梁的整体动态响应便能得到比较满意的精度.然而,Huang[50]指出对于复杂的桥梁结构用模态叠加法求解时,如果只考虑前面的若干阶模态将可能得不到准确的桥梁动力响应,在这种情况下需要采用直接积分法求解车桥耦合方程.

另外,Yang 和Lin[51]提出了由桥梁单元以及与桥梁直接接触的车辆悬挂装置单元组成的车桥相互作用单元.通过采用改进的动态缩聚法,把车辆所有的自由度都缩聚到开发的单元中,然后利用传统的有限元方法重组耦合方程,这样可大幅提高计算效率.

国内一些学者通过通用有限元分析软件ANSYS把车辆和桥梁视作两个分离的子体系,分别应用广义虚功原理和有限元法,推导各自的振动方程,然后通过接触点的位移协调方程和力平衡方程,用APLD语言把车辆和桥梁的振动耦合起来,建立车桥耦合振动方程,最后通过ANSYS的瞬态动力分析功能实现迭代求解[52-53].

4　影响IM的参数研究

4.1桥梁跨径和基频

桥梁基频被广泛认为是影响动力冲击系数的重要因素之一,很多桥梁规范甚至把动力冲击系数定义为桥梁基频的表达式.而桥梁的固有频率通常与其跨径相关.一些研究表明桥梁的基频随桥长的增加而降低[22,54-55].也有桥梁设计规范把IM规定为桥跨长的函数.但是,也有研究表明IM和桥跨长并无明确关系[8,23].还有研究表明当车辆和桥梁两者的振动频率接近时车辆和桥梁之间会发生准共振现象从而导致很大的IM[13,23,47,56].但也有学者指出频率对IM的影响并不大,车辆和桥梁的频率相近时IM也并不一定最大,他们认为车桥系统的相互作用受诸如车速、路面不平整度、桥梁频率等因素的综合影响[51,57].

4.2桥梁类型

研究者们通过现场试验和数值计算对不同类型的桥梁的IM进行了广泛的研究.在19世纪50年代到80年代期间,世界各国对不同类型的桥梁进行了大量的现场试验.在过去的20年内Huang和Wang通过数值模拟研究了不同类型桥梁的IM,包括钢筋混凝土梁桥[8,12,30,58]、拱桥[50,59]、斜拉桥[42-43]等.

多主梁桥是公路桥梁中最为普遍的一种桥型,因此对其冲击系数的研究较多.对I-型多主梁桥动力冲击系数的研究表明:(1)不同主梁上的IM不尽相同,承受荷载大的主梁上的IM一般较小[8,11,58]; (2)随着主梁间距的增大,内侧的主梁上的IM随之减小而外侧主梁上的IM基本不变[8,43]; (3)跨径或基频相同而截面形式不同的桥梁的IM相差可能较大[60]；(4)简支转连续梁后桥梁上的IM会减小[61].

对长桥IM的研究比短桥的研究更加困难,因而对长桥IM的研究相对较少.Huang和Wang[43]根据对斜拉桥的数值模拟发现:(1)斜拉桥中跨的铰链对IM的影响很大；(2)斜拉索的布置对IM的影响很小; (3)某些构件上的IM可能大于0.6.但是,Calçada[25]对斜拉桥的现场试验表明实测的IM最大值一般都小于0.2.Wang[62]根据对斜拉拱桥的数值模拟发现,不同构件上的IM有很大的区别,主要承重构件上的IM一般都小于0.33.关于拱桥的研究表明:(1)拱桥不同响应的IM随矢跨比有不同的变化趋势[59]；(2) 存在某个矢跨比使得主梁跨中挠度的冲击系数最小[63];(3) 拱桥的吊杆连接形式对IM的影响很小[50];(4)吊杆的IM与无应力索长成反比[63].

车辆荷载对曲线梁桥和直线梁桥的动力效应也有区别.对曲线箱梁桥的研究表明:(1)曲线箱梁桥的IM比相应的直桥小[64]；(2)IM随着曲线半径的减小而减小[12].当曲线半径大于1219m时,IM对曲线半径的变化不再敏感；但当曲线半径小于243m时,曲线半径的变化对IM影响很大[64]; (3)桥梁跨径和曲线半径的比率对IM有很大的影响[65].

4.3桥梁材料

关于桥梁材料对IM影响的研究较少.有些学者认为桥梁材料对IM的影响很小[2,21].一些国家的桥梁设计规范中区分了不同材料桥梁的IM设计值.中国[66]和日本[67]的桥梁设计规范对钢桥和混凝土桥采用不同的IM值.加拿大桥梁设计规范[6]规定木构件的IM需乘以折减系数0.7.而在美国AASHTO LRFD[5]规范中,考虑到木结构优良的阻尼特性而建议不需考虑动力冲击效应的影响.

近年来FRP材料因其高强、轻质和良好的抗腐蚀能力而被逐渐用于新桥的建设和既有桥梁的修复中.这种FRP新材料构件可能导致和传统材料桥梁不一样的动力特性.一些学者[68,69]比较了FRP梁板桥和混凝土梁板桥的IM,发现FRP桥梁上的IM要小很多.然而,FRP桥梁的阻尼比钢筋混凝土桥的阻尼小很多[15], 以此推断,IM应随着桥梁阻尼的减小而增大[16,43].

4.4路面不平整度

路面不平整度是引起车桥相互作用的主要激励.许多学者研究了IM与路面不平整度之间的关系.Park[70]根据25座桥梁的动力试验研究了路面不平整度和IM的关系,发现IM几乎与国际路面不平整度指数成线性关系.沈锐利通过数值模拟[71]研究了路面不平整度生成方法对IM的影响,发现使用三角级数叠加法生成的路面不平整度计算的IM样本服从正态分布,而使用离散傅里叶逆变换法生成的路面不平整度获得的IM样本服从极值Ⅰ型分布.通常基于后者获得的IM小于前者,且均大于规范的规定值.有些研究发现伸缩缝或引桥连接处引起的车辆初始振动会导致车桥耦合振动加剧而使桥梁构件承受很大的IM[49,72].

所有的研究几乎都表明IM随路面不平整度变差而大幅增大[10,43,48].差的路面状况是导致实际IM高于桥梁规范中IM规定值的主要原因[10,16,37].因此,对桥面进行维护是减小车辆荷载对桥梁冲击效应的有效方法.

4.5车重

很多研究表明IM随车重的增加而减小[8,26,48],这与IM随桥梁静响应的增大而减小的规律相对应[23,24,50].也有研究表明车辆在桥梁上的动力荷载效应大小并没有随车重增加而减小[61,73],还有学者发现桥梁的动静荷载效应都随车重的增加而增大[28,48].但以上所有的研究都表明IM随车重的增大而减小.需要指出的是轻车相比重车会产生更大的IM,但这并没有较大的实际指导意义,因为这种情况下对应的总荷载效应仍然较小.

4.6车辆悬挂系统类型

车辆的动力特性对动力冲击系数有较大的影响,其主要跟悬挂系统的刚度、阻尼等参数有关.一些研究表明具有气压悬挂系统的车辆比具有钢片悬挂系统的车辆会产生更小的IM,因为前者的阻尼更大[56,74].Kirkegaard[74]发现减少悬挂系统弹簧的刚度将导致更小的IM,而改变阻尼对IM基本没有什么影响.另外一些学者[19,31]也同样指出悬挂系统刚度大的车辆会产生更大的IM.但也有学者发现悬挂系统对IM的影响并不大[51].

避开车桥共振是减小冲击系数的一个重要考虑.为了使车辆的自振频率不落在一般桥梁的基频范围内,车辆(尤其是重车)的悬挂系统设计时需考虑这一点,但是在实际中却不容易做到.因此,有些学者建议车辆采用阻尼大的悬挂系统来减小IM[56].此外,也有学者提出采用车辆智能减振系统来减少车辆对桥梁的冲击效应[75].

4.7车辆加载位置

加载位置通过影响桥上轮载的分布和被激发的桥梁振动模态而影响桥梁的动力响应.Huang[8]发现混凝土梁桥不同主梁上的IM随车辆加载位置的变化而变化,随桥梁荷载分布系数的增大而降低.但是, 非对称加载时由于扭转模态被激发可能导致这个关系并不一定成立[13,16,73,74].从设计的角度来说,IM需根据最不利加载位置下的桥梁响应来计算.

4.8车数和轴数

许多研究表明多辆车作用下桥梁构件因承受较大的荷载效应而导致较小的IM[26,76].也有些研究表明两辆同类型车对称并排行驶时产生的IM和一辆车作用下产生的IM非常接近[10,77],这可能是由于两辆车同步与桥梁相互作用的结果.还有研究表明两辆车一前一后行驶产生的IM明显比两辆车并排行驶产生的IM小[26].需要注意的是很多情况下研究公路桥梁IM时采用的是一辆车或两辆车并行这种简单的荷载模型,这样通常会导致比实际交通状况下IM偏大的结果.

不同的车型(车轴数)同样也会影响动力冲击系数的大小.在加拿大的桥梁设计规范[6]中,IM定义为与车轴数相关的值.然而也有研究表明IM和车轴数量并没有确定关系[23,24].实际上,即使是轴数相同的车辆,不同的车重、轴距和悬挂系统特性也可能导致IM有较大的差别.

4.9车速

车速是影响IM的一个重要参数.一些学者发现IM随着车速的增加而增大[11,13,25,31].也有些学者指出IM和车速之间没有必然的联系[10,24,48,56].还有学者尝试把车速定义为没有量纲的速度参数[39,43,56],其表达式如下:

(7)

式中v表示车速；ωb表示桥梁的基频；L表示桥长.该参数S的物理意义是荷载频率和桥梁基频的比值.Smith[78]定义移动常荷载作用下简支梁上的IM为1/(1-S).此表达式表明IM随车速的增大而增大.Yang[51]发现移动荷载作用下简支和连续梁跨中的IM几乎和速度成线性关系.但Chatterjee[40]在研究车辆荷载作用下悬索桥的振动时发现IM的变化和速度参数没有必然的关系.

实际上,车速对IM的影响还跟其他很多因素相关.Hwang 和Nowak[79]发现IM随车速的变化跟车重相关.Huang[42]指出IM最大时对应的车速跟路面不平整度、桥长、研究点位置等因素相关.

综上可知,车速对IM的影响目前尚无定论,一方面原因在于不同的研究中采用的模型和方法不尽相同,另一方面也说明车速影响IM的机理非常复杂,车速可能与其他很多因素共同影响IM.

有些学者试图预测产生最大IM时对应的临界车速.如果能预测出临界速度,这对桥梁限速管理将有一定的指导意义.Shi[80]用如下公式预测临界车速:

(8)

式中v表示车速；Lv表示车轴间距；f表示桥梁的基频.该公式的物理依据是当轴载的激振频率和桥梁的基频相等时车桥系统会发生共振.通过此式预测的临界速度和数值模拟的结果吻合很好.然而该公式只适用于桥跨较短且车辆各轴的轴距基本相等的情况.

Brady[81]通过试验和数值模拟研究了简支梁在一个移动质点作用下的响应,发现存在一系列的速度对应着简支梁上较大的IM.González[32]把单质点荷载模型推广到和多轴车对应的一系列的质点荷载,并用试验证实了两辆车相对行驶时的确存在某个速度使得桥梁上的IM达到最大值.

不可否认上述研究对探讨最大IM产生的机理有一定的指导作用.但是,利用简单车辆和桥梁模型进行预测的结果具有一定的局限性.通过质点模型预测的速度的准确性随着车辆和桥梁的重量比的增大而变差.

此外,车桥振动的研究中通常假定车速为匀速,而实际交通情况下,车辆加减速的情况经常发生.一些学者指出在车辆制动时的IM会更大,且受制动位置等因素的影响[82,83].

需要强调的是,以上讨论的不同影响因素之间可能存在不同程度的交叉影响.比如对同一座桥梁,不同的参数如路面不平整度、荷载、车辆类型、不同构件类型等都会导致IM的不同.因此需要综合考虑多个因素的影响.然而,其中也有些因素对IM的影响受其他因素的交叉影响较小或者表现出对IM比较一致的影响规律,如IM随路面不平整度变差而增大,随车辆荷载效应的增大而减小.

5　各国桥梁规范中IM的规定

5.1中国规范

我国1989年版的公路桥涵设计通用规范[66]规定IM为桥跨长的函数.对于混凝土桥的主要结构构件,其IM用如下公式计算:

(9)

对于钢桥的主要结构构件,IM用下式计算:

(10)

以上两式中L均表示桥跨长.

而我国2004年版的公路桥涵通用设计规范[7]规定IM为桥梁基频的函数,如下式所示:

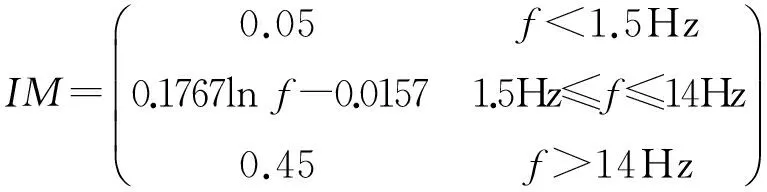
(11)

式中f表示桥梁的基频.

5.2日本规范

日本公路协会颁发的公路桥梁规范[67]定义冲击系数为桥跨长的函数,如表2所示.表2表明考虑卡车荷载动力效应时采用的IM对所有类型的桥梁都是一样的,而考虑车道荷载的动力效应时采用的IM跟桥梁类型有关.

表2　日本1996年JRA规范中规定的IM

L=span length (m).

5.3美国规范

1992年版美国AASHTO桥梁设计规范[4]定义IM为桥跨长的函数:

(12)

式中L表示桥跨长(m).并且规范规定车辆荷载和车道荷载都要考虑动力冲击效应.在1994年版AASHTO LRFD桥梁设计规范[84]中首次用新词“dynamic load allowance (DLA)”代替了原来“impact factor”的说法.DLA的取值根据极限状态和构件类型而定,如表3所示.这个规定一直沿用到目前(2012年版)的AASHTO LRFD桥梁规范[5].

美国现役钢桥和混凝土桥强度评估规范[85]则规定桥梁荷载评定使采用的IM需根据路面不平整度等级而定.如表4所示,IM的规定值随路面不平整度变差而增大.而在公路桥梁状态评估和荷载与抗力评定手册[86]中,桥梁强度和服役极限状态评定时的动力冲击系数取0.33.

表3　1994年AASHTO LRFD中DLA的取值规定

表4　1989年AASHTO荷载评定规范中的IM

5.4加拿大规范

1983年的加拿大公路桥梁设计规范[87]根据桥梁的第一阶弯曲频率确定IM,如图2所示.第一阶弯曲频率在2到5Hz的桥梁因容易与车辆产生准共振而采用了较大的IM设计值.1991年的加拿大公路桥梁设计规范[88]中规定IM的取值与车轴数相关,如表5所示.2006年的新版规范与1991年的公路桥梁设计规范[6]相比,唯一的区别在于桥面连接处的IM取值为0.5.

图2　1983年加拿大公路桥梁设计规范中规定的IMIM specified in the OHBDC (1983)

NumberofaxlesDLA10.420.33ormore0.25

5.5英国规范

英国钢桥、混凝土桥和组合桥规范[89](BSI 2006)规定了两种公路桥梁荷载,即规则和不规则交通荷载.两种荷载情况下IM都采用0.25.

5.6新西兰规范

新西兰交通部颁发的桥梁手册[90]根据桥跨长定义荷载动力系数(DLF,DLF=1+DLA).对于悬挂构件和桥面板的弯矩、支座反力和剪力,荷载动力系数取1.30.而对于简支或连续梁构件,荷载动力系数规定为桥跨长的函数:

(13)

式中L表示承受正弯矩的桥梁跨径或承受负弯矩的相邻跨径的平均值.

5.7澳大利亚规范

澳大利亚桥梁设计规范[91]规定IM根据车辆荷载配置而定,如表6所示.

表6　AS 5100规范中规定的DLA

上述规范规定的IM都是针对桥梁上部结构而言,而对于下部结构,规范规定的IM有所不同.通过上述对规范的回顾,可以发现:(1)不同国家的桥梁规范对IM的规定各不相同,很多规范把冲击系数定义为一些重要参数的表达式,如桥跨长[4,67,90]、交通荷载模型[89,91]、桥梁自振频率[7,87]等；(2)规范规定的IM形式一般较简单,考虑到的影响因素有限；(3) 规范中并没有明确规定计算IM的桥梁响应类型[92].

6　结论与展望

本文回顾了公路桥梁动力冲击系数的相关研究进展,根据已有的研究成果,得到以下主要结论,并提出了可以进一步研究的方向:

(1)不同类型桥型的IM和材料对IM的影响有待进一步研究.目前,桥梁设计规范大多没有区分不同类型桥梁的IM.而且,随着诸如FRP等轻质高强材料以及超高性能混凝土等在桥梁结构中越来越多的应用,不同材料对IM的影响值得关注.

(2)基于桥梁不同响应的IM之间的关系需要进一步明确.规范中针对桥梁不同响应类型的IM取值没有明确区分.例如,IM通常是根据桥梁跨中弯矩或位移这些整体荷载响应来确定,而根据这些响应确定的IM对桥梁局部结构的设计并不合理.

(3)路面不平整度是影响IM大小的主要因素.IM随路面不平整度变差而显著增大.因此,定期维护桥面是减小IM的有效手段.

(4)车辆速度是影响IM的重要因素之一.但车速对IM的影响机理复杂,目前两者的关系尚无定论,值得进一步研究.尤其是有些研究表明较低的车速也能引起较大的IM,值得引起重视.目前,铁路桥梁在这方面的研究已取得了一定的成果,可以参考借鉴.

(5)IM通常随车重的增加而减小,随桥梁荷载分布系数的增大而减小.这表明根据最不利加载位置和极限荷载计算的IM才有实际意义.此外,车辆的悬挂系统对IM有很大的影响,合理设计车辆悬挂系统能减小车辆的动力冲击作用.

(6)世界各国桥梁设计规范中对活荷载都有明确的定义.然而,关于哪部分活荷载需要考虑动力效应的规定并不一致.例如, 美国AASHTO LRFD规范中仅考虑了卡车荷载的动力效应而没考虑车道荷载的动力效应.通过这种荷载组合的活荷载效应能否准确反应车辆荷载作用下可能产生的最大荷载效应尚值得商榷.

(7)规范中的IM旨在为新桥设计提供依据.但评估现役桥梁,特别是路面很差的短桥时,规范中的IM取值可能偏小从而导致高估桥梁的实际承载力.这种情况下IM的取值需根据实际情况适当调整.

1Paultre P, Chaallal O, Proulx J. Bridge dynamics and dynamic amplification factors a review of analytical and experimental findings.CanadianJournalofCivilEngineering, 1992,19(2):260～278

2McLean D I, Marsh M L. Dynamic impact factors for bridges. NCHRP Synthesis 266. Washington, D.C.: Transportation Research Board, 1998

3李小珍, 张黎明, 张洁. 公路桥梁与车辆耦合振动研究现状与发展趋势.工程力学, 2008,25(3):230～240 (Li X Z, Zhang L M, Zhang J. Research status and development trend of highway vehicle-bridge coupled vibration.EngineeringMechanics, 2008,25(3):230～240 (in Chinese))

4American Association of State Highway and Transportation Officials. Standard specifications for highway bridges. Washington, D.C., 1992:1～19

5American Association of State Highway and Transportation Officials(AASHTO). AAASHTO LRFD bridge design specifications. 6thed. AAASHTO. Washington, D.C., 2012

6Canadian Standards Association. Canadian highway bridge design code. Ontario, Canada, 2006

7中华人民共和国交通部. 公路钢筋混凝土及预应力混凝土桥涵设计规范. 北京,中国,2004 (Ministry of Communications of PRC. Code for design of highway reinforced concrete and prestressed concrete bridges and culverts. Beijing, China, 2004 (in Chinese))

8Huang D Z, Wang T L, Shahawy M. Impact studies of multigirder concrete bridges.JournalofStructuralEngineering, 1993,119(8):2387～2402

9Liu C H, Huang D Z, Wang T L. Analytical dynamic impact study based on correlated road roughness.Computers&Structures, 2002,80(20):1639～1650

10Deng L, Cai C S. Development of dynamic impact factor for performance evaluation of existing multi-girder concrete bridges.EngineeringStructures, 2010,32(1):21～3111Chang D, Lee H Y. Impact factors for simple-span highway girder bridges.JournalofStructuralEngineering, 1994,120(3):704～715

12Huang D Z. Dynamic analysis of steel curved box girder bridges.JournalofBridgeEngineering, 2001,6(6):506～513

13Li H Y, Wekezer J, Kwasniewski L. Dynamic response of a highway bridge subjected to moving vehicles.JournalofBridgeEngineering, 2008,13(5):439～448

14Fafard M, Laflamme M, Savard M, Bennur M. Dynamic analysis of existing continuous bridge.JournalofBridgeEngineering, 1998,3(1):28～37

15Aluri S, Jinka C, GangaRao H V. Dynamic response of three fiber reinforced polymer composite bridges.JournalofBridgeEngineering, 2005,10(6):722～730

16Wang T L, Huang D Z, Shahawy M. Dynamic behavior of slant-legged rigid-frame highway bridge.JournalofStructuralEngineering, 1994,120(3):885～902

17Caprani C C. Probalistic analysis of highway bridge traffic loading.2005

18OBrien E J, Cantero D, Enright B, González A. Characteristic dynamic increment for extreme traffic loading events on short and medium span highway bridges.EngineeringStructures, 2010,32(12):3827～3835

19Szurgott P, Wekezer J, Kwasniewski L, Siervogel J, Ansley M. Experimental assessment of dynamic responses induced in concrete bridges by permit vehicles.JournalofBridgeEngineering, 2011,16(1):108～116

20Billing J R. Dynamic loading and testing of bridges in ontario.CanadianJournalofCivilEngineering, 1984,11(4):833～843

21Paultre P, Proulx J, Talbot M. Dynamic testing procedures for highway bridges using traffic loads.JournalofStructuralEngineering, 1995,121(2):362～376

22Cantieni R. Dynamic load tests on highway bridges in Switzerland-60 years of experience of empa. EMPA Report No 211. Dübendorf, Switzerland: Swiss Federal Laboratories for Materials Testing and Research, 1983

23Schwarz M, Laman J A. Response of prestressed concrete i-girder bridges to live load.JournalofBridgeEngineering,2001,6(1):1～8

24Laman J A, Pechar J S, Boothby T E. Dynamic load allowance for through-truss bridges.JournalofBridgeEngineering, 1999,4(4):231～241

25Calçada R, Cunha A, Delgado R. Analysis of traffic-induced vibrations in a cable-stayed bridge. Part i: Experimental assessment.JournalofBridgeEngineering, 2005,10(4):370～385

26Ashebo D B, Chan T, Yu L. Evaluation of dynamic loads on a skew box girder continuous bridge part i: Field test and modal analysis.EngineeringStructures, 2007,29(6):1052～1063

27Johnson D E, Johnson J R, Moore H P. A handbook of active filters. Englewood Cliffs, New Jersey: Prentice-Hall, 1980

28Chan T, O′Connor C. Wheel loads from highway bridge strains: Field studies.JournalofStructuralEngineering, 1990,116(7):1751～1771

29Zhu X Q, Law S S. Dynamic load on continuous multi-lane bridge deck from moving vehicles.JournalofSoundandVibration, 2002,251(4):697～716

30Wang T L, Huang D Z, Shahawy M. Dynamic behavior of continuous and cantilever thin-walled box girder bridges.JournalofBridgeEngineering, 1996,1(2):67～75

31Kwasniewski L, Li H Y, Wekezer J, Malachowski J. Finite element analysis of vehicle-bridge interaction.FiniteElementsinAnalysisandDesign, 2006,42(11):950～95932González A, OBrien E J, Cantero D, Li YY, Dowling J, Žnidaric A. Critical speed for the dynamics of truck events on bridges with a smooth road surface.JournalofSoundandVibration, 2010,329(11):2127～2146

33Dodds C J, Robson J D. The description of road surface roughness.JournalofSoundandVibration, 1973,31(2):175～183

34Honda H, Kajikawa Y, Kobori T. Spectra of road surface roughness on bridges.JournaloftheStructuralDivision, 1982,108(9):1956～1966

35International Organization for Standardization. Mechanical vibration-road surface profiles-reporting of measured data. ISO 8608:1995(E), ISO, Geneva, Switzerland, 1995.

36Oliva J, Goicolea J M, Antolín P, Astiz M. Relevance of a complete road surface description in vehicle-bridge interaction dynamics.EngineeringStructures, 2013,56:466～476

37Liu C H, Wang T L, Huang D Z. Impact study for multi-girder bridge based on correlated road roughness.StructuralEngineeringandMechanics, 2001,11(3):259～272

38Zhang W, Cai C S. Fatigue reliability assessment for existing bridges considering vehicle speed and road surface conditions.JournalofBridgeEngineering, 2011,17(3):443～453

39Yang Y B, Lin C W, Yau J D. Extracting bridge frequencies from the dynamic response of a passing vehicle.JournalofSoundandVibration, 2004,272(3):471～493

40Chatterjee P K, Datta T K, Surana C S. Vibration of suspension bridges under vehicular movement.JournalofStructuralEngineering, 1994,120(3):681～703

41Chompooming K, Yener M. The influence of roadway surface irregularities and vehicle deceleration on bridge dynamics using the method of lines.JournalofSoundandVibration, 1995,183(4):567～589

42Huang D Z, Wang T L. Impact analysis of cable-stayed bridges.Computers&Structures, 1992,43(5):897～908

43Wang T L, Huang D Z. Cable-stayed bridge vibration due to road surface roughness.JournalofStructuralEngineering, 1992,118(5):1354～1374

44Fafard M, Bennur M, Savard M. A general multi-axle vehicle model to study the bridge-vehicle interaction.EngineeringComputations, 1997,14(5):491～508

45Zhang Q L, Vrouwenvelder A, Wardenier J. Dynamic amplification factors and EUDL of bridges under random traffic flows.EngineeringStructures, 2001,23(6):663～67246Caprani C. Lifetime highway bridge traffic load effect from a combination of traffic states allowing for dynamic amplification.JournalofBridgeEngineering, 2013,18(9):901～909

47Kim C W, Kawatani M, Kim K B. Three-dimensional dynamic analysis for bridge-vehicle interaction with roadway roughness.Computers&Structures, 2005,83(19):1627～1645

48Broquet C, Bailey S F, Fafard M, Brühwiler E. Dynamic behavior of deck slabs of concrete road bridges.JournalofBridgeEngineering, 2004,9(2):137～146

49Cai C S, Shi X M, Araujo M, Chen S R. Effect of approach span condition on vehicle-induced dynamic response of slab-on-girder road bridges.EngineeringStructures, 2007,29(12):3210～3226

50Huang D Z. Vehicle-induced vibration of steel deck arch bridges and analytical methodology.JournalofBridgeEngineering, 2012,17(2):241～248

51Yang Y B, Liao S, Lin B H. Impact formulas for vehicles moving over simple and continuous beams.JournalofStructuralEngineering, 1995,121(11):1644～1650

52施颖, 宋一凡, 孙慧, 周新平. 基于ansys的公路复杂桥梁车桥耦合动力分析方法. 天津大学学报, 2010,43(6):537～543 (Shi Y, Song Y F, Sun H, Zhou X P. Dynamic analysis method of vehicle-bridge coupling for complicated bridges based on ANSYS.JournalofTianjinUniversity, 2010,43(6):537～543 (in Chinese))

53王凌波, 马印平, 蒋培文, 周勇军. 连续刚构体系车桥耦合振动敏感性参数研究. 合肥工业大学学报(自然科学版), 2014,37(8):901～906 (Wang L B, Ma Y P, Jiang P W, Zhou Y J. Sensitive parameter analysis of vehicle-bridge coupled vibration based on continuous rigid frame system.JournalofHefeiUniversityofTechnology, 2014,37(8):901～906 (in Chinese)

54Memory T J, Thambiratnam D P, Brameld G H. Free vibration analysis of bridges.EngineeringStructures, 1995,17(10):705～713

55Billing J R, Green R. Design provisions for dynamic loading of highway bridges.Transportation Research Record 950. Washington, D.C.,Transportation Research Board, 1984:94～103

56Green M F, Cebon D, Cole D J. Effects of vehiclesuspension design on dynamics of highway bridges.JournalofStructuralEngineering, 1995,121(2):272～282

57Pan T C, Li J. Dynamic vehicle element method for transient response of coupled vehicle-structure systems.JournalofStructuralEngineering, 2002,128(2):214～22358Huang D Z, Wang T L, Shahawy M. Impact analysis of continuous multigirder bridges due to moving vehicles.JournalofStructuralEngineering,1992,118(12):3427～3443

59Huang D Z. Dynamic and impact behavior of half-through arch bridges.JournalofBridgeEngineering, 2005,10(2):133～141

60邓露, 何维, 王芳. 不同截面类型简支梁桥动力冲击系数研究.振动与冲击, 2015,34(14):70～75 ( Deng L, He W, Wang F. Study of dynamic impact factors of simply-supported concrete bridges with different cross sections.JournalofVibrationandShock, 2015,34(14):70～75 (in Chinese))

61桂水荣, 陈水生, 万水. 汽车荷载作用下空心板桥空间动力冲击效应.北京交通大学学报, 2014,38(1):70～76 (Gui S R, Chen S S, Wan S. Spatial dynamic impact effects of hollow slab bridge subjected to moving vehicle.JournalofBeijingJiaotongUniversity, 2014,38(1):70～76 (in Chinese))

62Wang W, Yan W C, Deng L, Kang H J. Dynamic analysis of a cable-stayed concrete-filled steel tube arch bridge under vehicle loading.JournalofBridgeEngineering, 2014,DOI: 04014082

63霍学晋, 蒲黔辉. 蝶形拱桥的动力冲击系数研究.振动与冲击, 2014,33(1):176～182 (Huo X J, Pu Q H. Impact factors of butterfly-shaped arch bridges.JournalofVibrationandShock, 2014,33(1):176～182 ( in Chinese))

64Schelling D R, Galdos N H, Sahin M A. Evaluation of impact factors for horizontally curved steel box bridges.JournalofStructuralEngineering, 1992,118(11):3203～3221

65Samaan M, Kennedy J B, Sennah K. Impact factors for curved continuous composite multiple-box girder bridges.JournalofBridgeEngineering, 2007,12(1):80～88

66中华人民共和国交通部. 公路钢筋混凝土及预应力混凝土桥涵设计规范. 北京,中国, 1989 ( Ministry of Communications of PRC. Code for design of highway reinforced concrete and prestressed concrete bridges and culverts. Beijing, China, 1989 (in Chinese))

67Japan Road Association.Specifications for highway bridges, part 1, common specifications. Tokyo, Japan,1996.

68Zhang Y, Cai C S, Shi X M, Wang C. Vehicle-induced dynamic performance of FRP versus concrete slab bridge.JournalofBridgeEngineering, 2006,11(4), 410～419

69Hag-Elsafi O, Albers W F, Alampalli S. Dynamic analysis of the bentley creek bridge with FRP deck.JournalofBridgeEngineering, 2012,17(2):318～333

70Park Y S, Shin D K, Chung T J. Influence of road surface roughness on dynamic impact factor of6 bridge by full-scale dynamic testing.CanadianJournalofCivilEngineering, 2005,32(5):825～829

71沈锐利,官快,房凯. 车桥耦合数值模拟桥梁冲击系数随机变量的概率分布. 振动与冲击, 2015(18):123～128 (Shen R L, Guan K, Fang K. Probability distribution of random variables of impact coefficient in numerical simulation of vehicle-bridge coupled vibration.JournalVibrationandShock, 2015(18):123～128 (in Chinese))

72Deng L, YanW C, Zhu Q J. Vehicle impact on the deck slab of concrete box-girder bridges due to damaged expansion joints.JournalofBridgeEngineering, 2015,DOI:06015006

73Moghimi H, Ronagh H R. Impact factors for a composite steel bridge using non-linear dynamic simulation.InternationalJournalofImpactEngineering, 2008,35(11):1228～1243

74Kirkegaard P H, Neilsen S RK, Enevoldsen I. Heavy vehicles on minor highway bridges calculation of dynamic impact factors from selected crossing scenarios. Paper No 172. Aalborg, Denmark: Dept. of Building Technology and Structural Engineering, Aalborg Univ., 1997:1～19

75Harris N K, OBrien E J, González A. Reduction of bridge dynamic amplification through adjustment of vehicle suspension damping.JournalofSoundandVibration, 2007,302(3):471～485

76Wang T L, Huang D Z, Shahawy M. Dynamic response of multigirder bridges.JournalofStructuralEngineering, 1992,118(8):2222～2238

77Kashif A M. Dynamic response of highway bridges to moving vehicles. Ottawa, Ontario, Canada: Department of Civil and Environmental Engineering, Carleton University, 1992

78Smith J W. Vibration of structures: Applications in civil engineering design. New York: Chapman and Hall, 1988

79Hwang E S, Nowak A S. Simulation of dynamic load for bridges.JournalofStructuralEngineering, 1991,117(5):1413～1434

80Shi X M, Cai C S, Chen S R. Vehicle induced dynamic behavior of short-span slab bridges considering effect of approach slab condition.JournalofBridgeEngineering, 2008,13(1):83～92

81Brady S P, O′Brien E J, Žnidaric A. Effect of vehicle velocity on the dynamic amplification of a vehicle crossing a simply supported bridge.JournalofBridgeEngineering, 2006,11(2):241～249

82Deng L, Wang F. Impact factors of simply supported prestressed concrete girder bridges due to vehicle braking.JournalofBridgeEngineering, 2015,DOI:06015002

83Yin X F, Fang Z, Cai C S, Deng L. Non-stationary random vibration of bridges under vehicles with variable speed.EngineeringStructures, 2010,32(8):2166～2174

84American Association of State Highway and Transportation Officials.LRFDbridge design specifications. Washington, D.C., 1994

85American Association of State Highway and Transportation Officials. Guide specifications for strength evaluation of existing steel and concrete bridges. Washington, D.C., 1989:1～19

86American Association of State Highway and Transportation Officials. Guide manual for condition evaluation and load and resistance factor rating (LRFR) of highway bridges. Washington, D.C., 2003

87Ontario Ministry of Transportation and Communications. 1983 ontariohighway bridge design code. 2nd Ed, Ontario, Canada, 1983

88Ontario Ministry of Transportation and Communications. 1991 ontariohighway bridge design code. 3nd Ed, Ontario, Canada, 1991

89British Standard Institution. Bs 5400-2: Steel, concrete and composite bridges. Part 2: Specification for loads. London, United Kingdom, 2006

90New Zealand Transport Agency. Bridge manual. Wellington, New Zealand, 2013

91Austroads. As 5100 bridge design standard—part 2: Design load. Sydney, Australia, 2004.

92Yu Y, Deng L, Wang W, Cai C S. Local impact analysis for deck slabs of prestressed concrete box-girder bridges subject to vehicle loading.JournalofVibrationandControl, 2015, DOI:1077546315575434

*The project supported by the National Natural Science Foundation of China (51208189, 51478176) and Excellent Youth Foundation of Hunan Scientific Committee (14JJ1014)

† Corresponding author E-mail: denglu@hnu.edu.cn

17 January 2016,revised 21 January 2016.

RESEARCHPROGRESS ON DYNAMIC IMPACT FACTORS OF HIGHWAY BRIDGES*

Deng Lu1,2†Wang Wei2

(1.KeyLaboratoryforWindandBridgeEngineeringofHunanProvince,HunanUniversity,Changsha410082,China)(2.CollegeofCivilEngineering,HunanUniversity,Changsha410082,China)

The research progress in the area of dynamic impact factors (IM) of highway bridges during the past two decades was reviewed in the paper. The definition ofIMwas first introduced. Then, related progress and findings from both field studies and numerical simulations were summarized. Parameters that affect theIMwere discussed in details and provisions relevant to theIMin bridge design codes of many countries around the world were reviewed. Finally, based on the advances achieved in this field, some conclusions were drawn and much effort was made to identify the remaining controversies and gaps left in this field.

vehicle-bridge coupled interaction,dynamic impact factors,field test,numerical simulation

E-mail: denglu@hnu.edu.cn

10.6052/1672-6553-2016-15

2016-01-17收到第1稿,2016-01-21收到修改稿.

*国家自然科学基金资助项目(51208189、51478176)和湖南省杰出青年基金资助项目(14JJ1014)