概念起始课,我们不能走得太远
——由一节随堂课说起
☉江苏省东台市时堰镇中学姜跃琪
概念起始课,我们不能走得太远
——由一节随堂课说起
☉江苏省东台市时堰镇中学姜跃琪
在初中阶段,概念是数学新授课教学的最主要的内容.上好概念起始课,将有利于学生深刻理解概念、应用概念.那么,在这样的课上,我们究竟该走多远呢?这个话题一直困扰我们这些一线教师.对此,由于教学内容和学情的不同,课堂教学存在着很大的“变数”,“该走多远”几乎无法给出定论.于是乎,有老师就错误地认为“能走多远就走多远”.在近期的一次随堂听课中,一位老师执教人教版七年级下册“6.1平方根(第1课时)”时,便将此想法落在了实处,不仅教完了教材给出的内容,还将知识进行了进一步拓展,课堂容量很大,但取得的效果却并不好.现呈现这节课的简录并谈一些个人的看法,不对的地方,敬请批评指正.
一、“6.1平方根”(第1课时)教学过程简述
在经历了情境引入和概念抽象两个环节后,教师顺利地揭示了“算术平方根”的概念及其符号表示,共耗时15分钟.在接下来的30分钟时间内,教师先后呈现了下面的例1至例6,并以这些例题的教学来带领学生巩固和应用刚刚获得的概念.
例1求下列各数的算术平方根:
学生快速给出了答案,教师并没有对学生获得结果的过程进行追问,两分钟的交流后,便安排学生记忆11到20的平方.3分钟后,教师在黑板上写出121、324两个数,请学生说说它们的算术平方根,有两名学生很快给出了答案,教师让学生将11到20的平方结果写在了书上.
例2分别求下列各式的值:
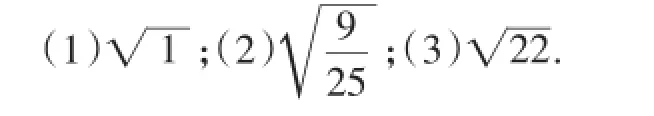
四名学生进行了板书,老师点评并归纳出求值的一般思路:找出平方等于被开方数的那个正数.
学生答:正数.
教师追问:可以为0吗?
在得到学生的肯定结论后,教师继续追问:那么,a呢?
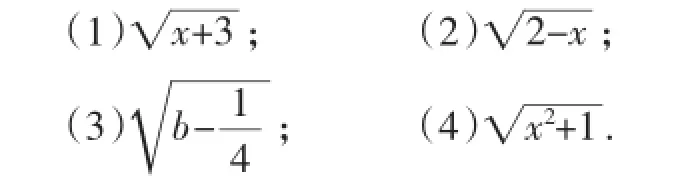
例3下列各式中哪些有意义?哪些无意义?为什么?
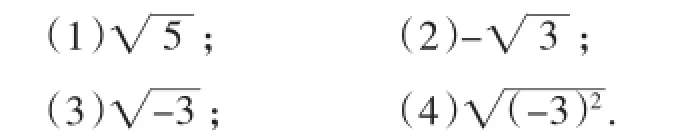
在学生给出结论后,教师追问:为什么没有意义?式子有意义的条件是什么?进而引出例4.
例4下列各式有意义的条件是什么?
学生尝试解答,教师请两位学生板书,并对学生给出的解题过程进行了纠正,形成了如下“规范”过程:
所以3-x≥0,x-3≥0.
所以x=3.(得出这一结论,耗时颇多)
所以y=6.
所以x+y=9.
所以x+y的算术平方根是3.
与例5的教学一样,教师仍然是请学生板书,在教师准备纠正学生解题过程时,下课铃声响了起来.
二、过程简析及改进建议
在初中阶段,几乎所有的代数概念都是从实际情境中抽象出来的.算术平方根也不例外,在这样一节概念起始课上,教师花15分钟时间来抽象概念并介绍其符号表示,这在初中阶段的概念教学中应该是中规中矩的.但是耗费30分钟时间来巩固和应用概念,这在概念教学中确实是较为少见的.下面,我们从这6道例题及其教学过程来进行详细的分析.
例1是教材中例题的“同型题”,只是数据的调整,“求各数的算术平方根”实际上是对本节课概念的直接应用.显然,教材例题设计的意图并没有被教者“读懂”,教学进程中,几名优秀学生的正确答案迅速替代了其他学生的思维,教师误认为全体学生都已经理解并会应用算术平方根的概念,这对后续平方根和立方根的学习是十分不利的.
改进建议:我们最起码应让学生弄清楚是怎么去求算术平方根的,也就是要呈现出教材例题的解题过程,以第(1)题为例,其分析与解答过程应为“因为22=4,所以4的算术平方根为2,即=2”,这样不仅有利于学生深刻理解概念的本质,还为后面的学习积累了丰富的分析问题和解决问题的经验.
例2来自于教材第41页的练习,“求下列各式的值”是符合算术平方根的化简.教学过程中,教者没有对所给式子的含义进行深挖,与例1的教学一样,都是“蜻蜓点水”式地一带而过.少部分学生的正解掩盖了绝大多数学生的概念学习现状,这对今后的教学没有任何好处.接下来,平方根、立方根的加入,三个概念的混淆将无法避免,到那时,再想去理清这些概念就十分困难了.
改进建议:在学生给出结果后,就每一个式子进行分析,“这个式子表示什么”,“怎么求”,“你是怎么想到这个结果的”,以这样的问题组引导学生理清式子的含义,并形成计算求值的“思维链”.这样一来,不仅顺用了本节课获得的概念,还将例1的解题经验进一步强化.
改进建议:保留例3和例6,删去例4和例5.在例3和例6的教学中,应突出所给式子含义的解读,将算术平方根的含义教学一直放在最前沿,让学生时刻感知其应用价值.
三、几点思考
1.走得太远,重点不再是重点,难点却成为了真正的难点
概念起始课,真的不宜走得太远.我们只有45分钟的教学时间,有的地方甚至只有40分钟的教学时间,在这么短的时间内我们能让学生学到的知识是有限的.如果一味地增加教学内容,原本准备突破的教学重点和难点将会成为教学的障碍,教材所预设的教学重点将会在教学上产生很大的偏移,重点将不再是教学的重点,而难点却会成为学生认知的真正难点.这种现象出现的征兆就是课上的“冷场”,而且会反复多次出现.学生以无声的“抗拒”,来告诉老师“你的教学走得太远了”.正如这里所言,本文中“算术平方根”的教学,其重点和难点都应是算术平方根的概念.教师在叠加了很多与本课时无关的教学内容后,例题的多轮“轰炸”弱化了重点,学生在问题解决过程中并没有能够对概念进行更进一步的认知,而是纠结于一些新的知识的应用,本节课的重难点没有得到很好的解决,新的问题又随之而来,教学效果自然不会好到哪里.
2.概念应用应立足于学生现有认知水平之上
不管是什么学生的教学,都应建立在学生的“最近发展区”之上.维果斯基将学生的学习水平分为两种:一种是学生已有的水平,还有就是学生即将到达的水平,这两者之间的差距就是最近发展区.因此,我们的教学设计应从分析学生的最近发展区开始,应充分分析学生的已有认知水平,确保新的概念建立在学生原有的概念之上.当然,对新概念的应用,也应立足于学生的现有认知水平,绝不可建构空中楼阁,让学生不仅碰不到,而且连想都无法想.还是结合上面的案例来说,不等式组的解法在人教版教材中被安排在七年级下册第九章,虽然离本单元不远,但毕竟是“后知”,学生尚未获得,在这样一节概念起始课上,就要求学生将后面的知识挪到前面来用,这不是难为学生吗?所以,笔者认为,这样的教学是教师的教学态度出了问题,对这位老师的做法笔者是不赞同的.教学设计,应以尊重学生、尊重数学、尊重教学为前提,不可盲目自大,更不可好高骛远,设计学生能够实现的教学过程应该成为一线教师的主流追求.
3.概念起始课应重视概念本质的教学
起始,即开始,上一节概念起始课就应该上出“出发”的味道,我们不可能也没有必要在一节课上将概念的内涵和外延都说得清清楚楚.“重点突出”是我们对每一节数学课的要求,这对概念起始课尤为重要.课上,我们不仅要强化对概念的认知,还应为后续教学建构出有效的生长点,以便后面的学习能在这里顺延下去.在概念起始课上,我们创设合适的问题情境,引导学生感知其中隐藏的概念,并适时从中抽象出具有共性特征的文字、符号或图形,借助生活实例与数学事实的比对,帮助学生理清概念的本质,为接下来的应用铺路搭桥.本文中的这位老师教学重点偏离了方向,他没有关注算术平方根本身的教学,而是将应用作为这节起始课的重点,抢着去完成本章后几课的任务,但又没有做好;抢着去教“二次根式”的内容,由于不等式(组)成为了学生无法逾越的障碍,得不偿失.课后,笔者与这位老师进行了交流,大家一致认为,这节课还是应立足于算术平方根本身的认知之上进行微量的拓展.在一节新单元的起始课上,将这么多的例题同时抛出,不仅不利于学生获得当节课的知识,而且还会对后面的数学学习产生诸多不利的影响.
四、写在最后
我们常说,数学教学要有“数学味”,很多老师认为所谓的“数学味”就是用数学知识解决实际问题或数学问题.这种观点将数学应用性定位为数学教学的重心,笔者认为是不妥的.如果我们都是重视概念的应用,从学生开始接触概念就用一道又一道的例题来强化巩固,那么学生获得新知的新鲜感和喜悦感何在?数学概念是生来有用的,但我们绝不能急在一时,要立足当下,放眼长远,从把握概念的本质出发,让学生在学好概念的情况下再去用概念,只有遵循了数学教学循序渐进的原则,我们的概念教学才能善始善终,为学生的长远发展服务!H

