让定理在实验操作中"自然生成" ---听"线段、角的轴对称性(1)"有感

江苏省无锡市蠡园中学　周进荣江苏省无锡市蠡园中学　王燕

.江苏省无锡市王华民数学名师工作室.

让定理在实验操作中"自然生成"
---听"线段、角的轴对称性(1)"有感

最近,滨湖区王华民数学名师工作室组织了一次听、评课活动,格致中学的尤晓珍老师执教了一节研究课---"线段的轴对称性".本课中,尤老师将数学实验引入课堂教学,让线段垂直平分线的性质定理及逆定理在实验操作中自然生成,取得了较好的教学效果,引起大家的共鸣.下面将本节课的部分教学片段予以展示,与同行交流.

一、教学片段

1.创设情境,激发兴趣

师:在一张薄纸上画一条线段AB,如图1,你能找出与线段AB的端点A、B距离相等的点吗?这样的点有多少个?

图1

(学生尝试找点)

生1:线段AB的中点与端点A、B的距离相等.

师:还有吗?

生2:还有,好像在线段AB的中点的上下位置.

(具体在哪里,学生一时无法准确表达)

师:相信通过本节课的学习,我们一定能解决该问题!

2.引入实验,探索定理

(1)画一画、折一折.

请你准备一张薄纸,在这张薄张上任意画一条线段AB,如图2,折纸,使两端点A、B重合,如图3所示.

图2

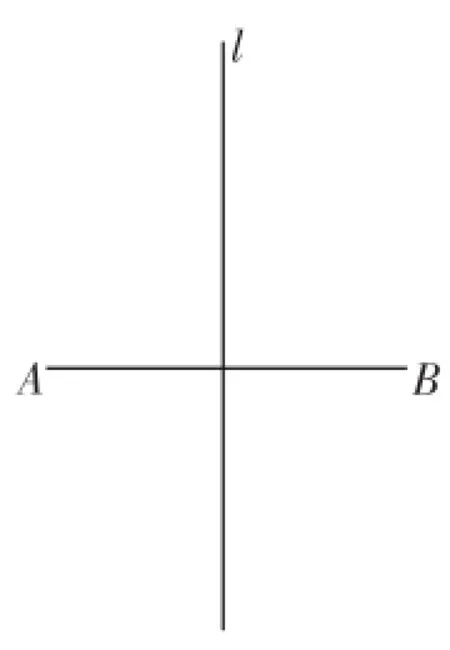
图3

师:按要求对折线段后,你有什么发现?

生3:线段AB是轴对称图形,折痕l是它的对称轴.

生4:折痕l是线段AB的垂直平分线.

(2)猜一猜、量一量.

师:如图4,在线段AB的垂直平分线l上任意找一点P,连接PA、PB,猜想PA与PB有何数量关系.量量看!

生5:PA=PB.

图4

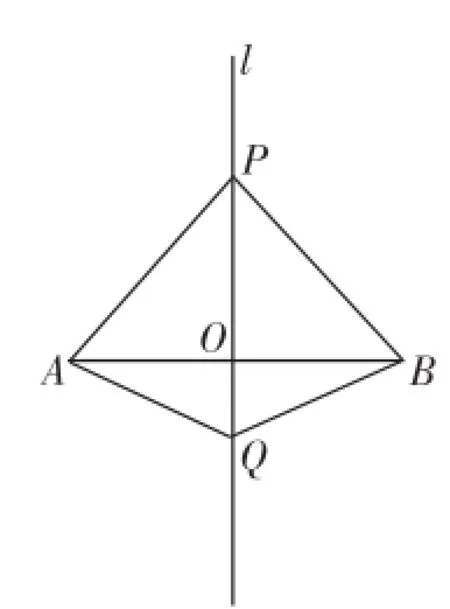
图5

(3)想一想、证一证.

师:如图5,在线段AB的垂直平分线l上另外找一点Q,连接QA、QB,QA与QB还有上述的数量关系吗?说说你的理由.

生6:还有上述相等关系,可用"SAS"证明△QAO≌△QBO,可知QA=QB.

师:类似于P、Q这样的点有多少个?它们都有什么样的特征?

生7:类似于P、Q这样的点有无数个,它们到点A、B的距离都相等!

师:好,我们把上述特征称为线段的垂直平分线的性质定理.谁能用简洁的语言概括一下?

生8:线段垂直平分线上的一点到线段两端点的距离相等.

师:如图6,若点P是线段AB的垂直平分线l外一点,那么PA与PB还相等吗?量量看,说说你的理由.

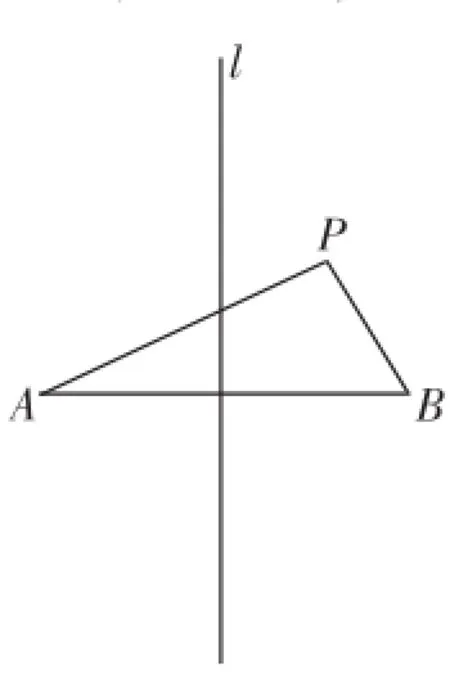
图6

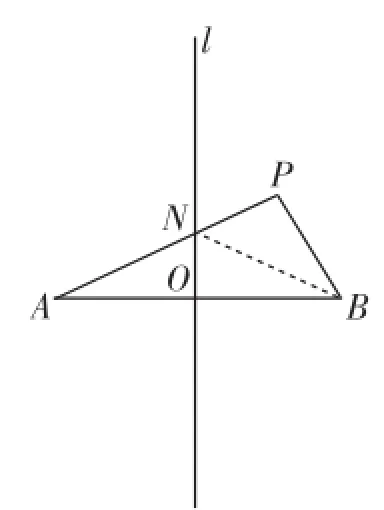
图7

生9:PA与PB不相等,显然PA>PB.

师:能证明吗?

生10:如图7,连接NB,由于点N在直线l上,由线段垂直平分线定理可知:AN=BN,所以PA=AN+NP=BN+NP> PB.

师:通过上面的探索,我们又有什么发现?

生11:线段垂直平分线外的一点到线段两端点的距离不相等.

……

(4)猜一猜、画一画.

师:如果一个点在一条线段的垂直平分线上,那么这个点到这条线段两端的距离相等.反过来,如果一个点到一条线段的两端的距离相等,那么这个点在这条线段的垂直平分线上吗?

生12:如图8,若点Q在线段AB上,且QA=QB,则Q是线段AB的中点,显然点Q在线段AB的垂直平分线上,如图9.

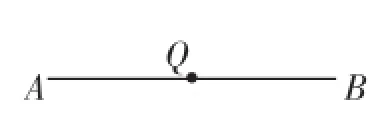
图8

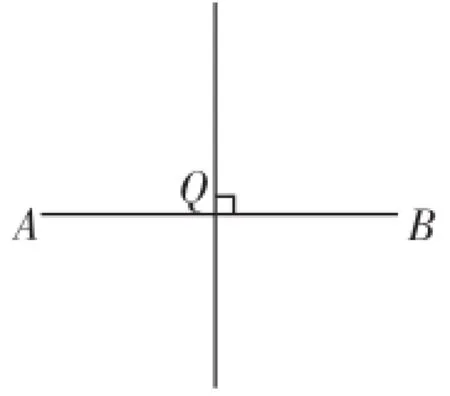
图9

师:若点Q是线段AB外任意一点,且QA=QB,如图10,那么点Q在线段AB的垂直平分线上吗?为什么?

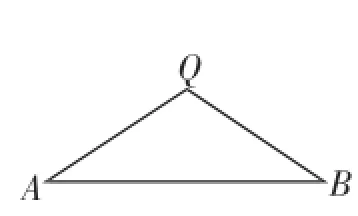
图10

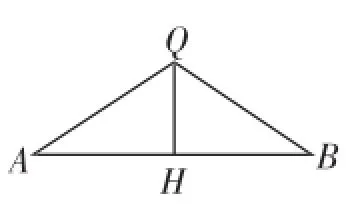
图11

生13:如图11,过点Q作QH⊥AB于点H,利用"HL"证明三角形全等,可得到QH垂直平分AB.

生14:如图11,过点Q作∠AQB的角平分线交AB于点H,利用"SAS"证明三角形全等,也可得到QH垂直平分AB.

生15:如图11,过点Q作AB边上的中线交AB于点H,利用"SSS"证明三角形全等,同样可得到QH垂直平分AB.

师:通过上述探索,你又有什么发现?

生16:如果有一点到线段两端点的距离相等,那么这个点在线段的垂直平分线上.

师:我们把它称为线段垂直平分线的判定定理,它与性质定理有何关系?

生17:它是性质定理的逆定理.

图12

3.运用定理,解决问题

(1)想一想、说一说.

师:在一张薄纸上画一条线段AB,如图12,你能找出与线段AB的端点A、B距离相等的点吗?这样的点有多少个?

生18:根据线段垂直平分线的判定定理,这样的点有无数个,它们都在线段AB的垂直平分线上. (首尾呼应,学生学以致用) (2)想一想、画一画.

师:你能运用所学知识,用尺规画出任一条线段的垂直平分线吗?如果能,说说你作图的依据.

(学生尝试画一条线段的垂直平分线)

图13

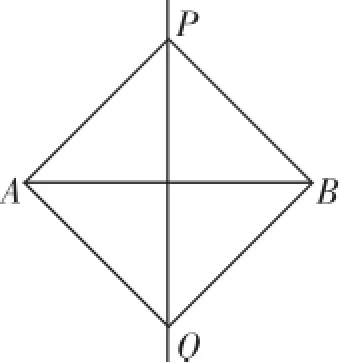
图14

师:这样做的依据是什么?

生20:在用尺规作图的过程中,因为PA=PB,所以点P在AB的垂直平分线上;因为QA=QB,所以点Q也在AB的垂直平分线上.由于两点确定一条直线,故PQ是AB的垂直平分线.

……

二、几点思考

(1)《义务教育数学课程标准(2011年版)》指出:"学生学习应当是一个生动活泼的、主动的和富有个性的过程.认真听讲、积极思考、动手实践、自主探索、合作交流等,都是学习数学的重要方式.学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程."在数学教学中,让学生变"听"数学为"做"数学,变"被动接受"为"主动探究",通过"做"数学实验体验发现的乐趣,感悟数学的真谛,发展数学思维和智慧,提高实践能力和创新意识,逐步积累数学活动经验.

(2)传统数学课堂教学压缩了学习知识的思维过程,往往造成感知与概括之间的思维断层,既无法保证教学质量,更不可能发展学生的学习策略.新课程理念提倡重视过程教学,在揭示知识生成规律上,让学生自己动手实验,不断尝试、感悟,自己去发现数学定理,从而使学生对定理的理解更深刻.

(3)本节课教学设计流畅、合理,重点、难点突出.从学生熟悉的问题入手,让学生带着疑问有针对性地听课,探索并证明了线段的垂直平分线的性质定理及其逆定理,学会用直尺和圆规作线段的垂直平分线,以"问题串"的形式引发学生思考,并加以适当的追问,培养学生思考问题的严谨性和表达的条理性,在本节课的最后又通过所学知识解决了问题,使学生的思维得到了进一步的提升.学生经历了"作图-猜想-证明"的过程,发展了空间观念和演绎推理的能力.可以说是学以致用,首尾呼应,效果很不错.

(4)实验教学活动中的"操作-思维"互不可分,操作是前导,思维是关键,学生通过动手做实验,增加感性认识,丰富大脑的表象,促进学生把外界生活实际和感知与内隐的思维活动紧密联系起来,使他们的形象思维和抽象思维协调发展,促使其感性认识深化为理性,提高其思维能力.

(5)数学定理的抽象性通常都有某种"直观"的想法为背景.作为教师,就应该通过实验,把这种"直观"的背景显现出来,帮助学生抓住其本质,了解它的变形和发展及与其他问题的联系.本节课老师让学生通过一系列的动手操作,让学生经历探索线段的轴对称的过程,在"操作-探究-归纳-证明"的过程中不断尝试、感悟,让定理在实验操作中自然生成,学生在轻松的环境中掌握了知识,寓教于乐!