"一题一课":简约并不简单---以2015年浙江台州中考卷第24题教学为例

浙江省余姚市梨洲中学　赵旭军

"一题一课":简约并不简单
---以2015年浙江台州中考卷第24题教学为例

中考把关试题往往都是经过充分的打磨、苦心经营而推出的,既承担了必要的选拔区分功能,又传递着教学导向,值得老师们认真思考,在贯通思路、洞察问题结构之后,还可将考题设计成习题课,开发成"一题一课" (相关观点,受益于文1),引导学生深入思考.本文选取2015年浙江台州一道把关题,简述求解思路之后,给出该题的习题解题教学设计,抛砖引玉,供研讨.

一、考题与思路简述

考题:(2015年浙江台州)定义:如图1,点M、N把线段AB分割成AM、MN和BN,若以AM、MN、BN为边的三角形是一个直角三角形,则称点M、N是线段AB的勾股分割点.

(1)已知点M、N是线段AB的勾股分割点,若AM=2, MN=3,求BN的长.

(2)如图2,在△ABC中,FG是中位线,点D、E是线段BC的勾股分割点,且EC>DE≥BD,连接AD、AE分别交FG于点M、N,求证:点M、N是线段FG的勾股分割点.

图1

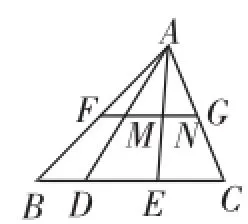
图2

(3)已知点C是线段AB上的一定点,其位置如图3所示,请在BC上画一点D,使C、D是线段AB的勾股分割点. (要求尺规作图,保留作图痕迹,画出一种情形即可)

(4)如图4,已知点M、N是线段AB的勾股分割点, MN>AM≥BN,△AMC、△MND和△NBM均是等边三角形,AE分别交CM、DM、DN于点F、G、H.若H是DN的中点,试探究S△AMF、S△BEN和S四边形MNHG的数量关系,并说明理由.

图3

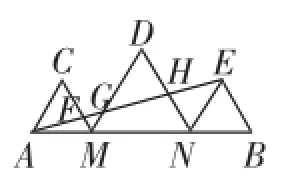
图4

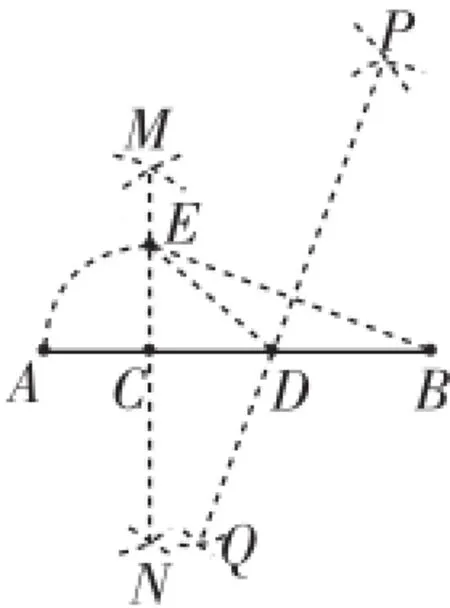
图5

(2)先由三角形中位线性质得出BD=2FM,DE= 2MN,EC=2NG,再由已知可得(2NG)2=(2MN)2+(2FM)2,即4NG2=4MN2+4FM2.于是NG2=MN2+FM2.问题获证.

(3)可以先构造草图分析,只有把三条线段置于一个直角三角形中才能实现目标,于是构造图5实现:①过点C作AB的垂线MN;②在MN上截取CE= CA;③连接BE,作BE的垂直平分线PQ交AB于点D.则点C、D是线段AB的勾股分割点.

(4)解读条件"△AMC、△MND和△NBM均是等边三角形"可以有很多发现,比如AC∥MD∥NE,CM∥DN∥BE.再结合条件"H是DN的中点"可以发现△DGH≌△NEH.设AM=a,BN=b,MN=c,经过转化可以把GM用含b、c的式子表示,从而利用△AGM∽△ANE,得比例式,转化为c2=2ab-ac+bc.再结合已知条件勾股分割点得出c2=a2+b2,可推出(a-b)2=(ba)c.又b-a≠c,所以a=b.也就是图4中两侧的两个小等边三角形是全等的,它们的面积也就相等.再由c2=a2+b2,便得到,即S△DMN=S△ACM+S△ENB.又 S△DMN=S△DGH+S四边形MNHG,S△ACM=S△CAF+S△AMF,S△ACF=S△DGH= S△NEB,所以S四边形MNHG=S△AMF+S△BEN.

二、解题教学设计

(一)开课阶段,给出定义

给出上文"考题"的定义,略.

反射光分布测量装置如图2所示[9]。激光辐照在样品表面，通过改变激光入射方向入射角度，利用半圆阵列分布的光电探测器收集散射光，实现各路信号的光电转换，利用数据采集记录探测阵列的输出信号。利用所设计的实验装置，对不同材料粗糙表面、不同入射角度粗糙表面及同一材料不同表面粗糙度的BRDF特性开展了实验测试，测试的散射光强分布用归一化值进行表征[10]。

设计意图:在给出定义之后,安排一组含30°、45°的特殊直角三角形的三边比值,让学生理解勾股分割点,同时又复习一下特殊直角三角形.这里我们改编了考题第一问相关数据,主要考虑是削枝强干,把学生思维聚焦在新定义上.

(二)尺规作图,作"勾股分割点"

问题3:如图6,阅读以下作图语句:①在AB取一点C,作CE⊥AB,取CE=CA;

②连接BE,作BE的垂直平分线,交AB于点D.

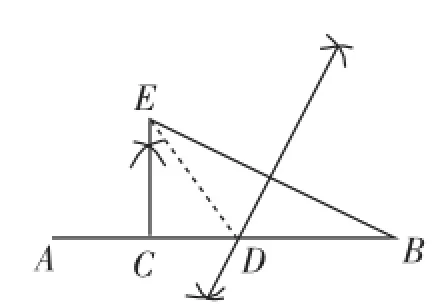
图6

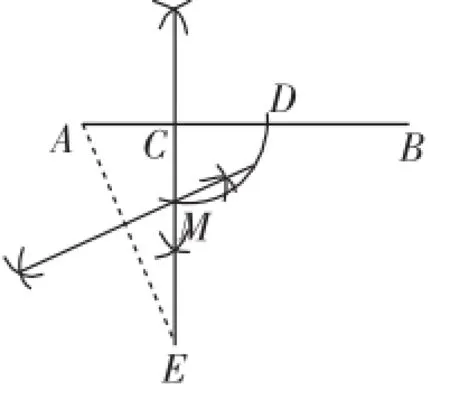
图7

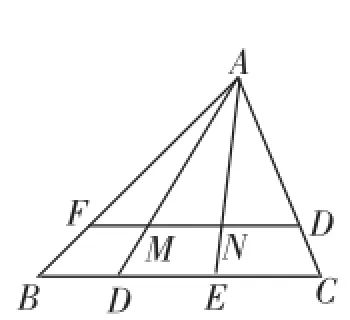
图8

设计意图:通过阅读作图语句,理解作法之后,连接DE,可以将三条线段AC、CD、BD集中在直角三角形CDE中,利用勾股定理得出它们之间的平方关系,从而确认C、D是线段AB的勾股分割点.根据学生的理解水平,还可以设计相关追问,比如还有其他的作法吗?以下提供一种不同的作法:如图7,作CE垂直AB,取CE=CB,连接AE,作AE的垂直平分线交CE于M,在CB上截取CD=CM,则点C、D是线段AB的勾股分割点.

(三)变式思考,成果扩大

问题4:(改编自考题的第三问)如图2,在△ABC中, FG是中位线,点D、E是线段BC的勾股分割点,且EC> DE≥BD,连接AD、AE,分别交FG于点M、N,点M、N会是线段FG的勾股分割点吗?为什么?

成果扩大:如图8,在△ABC中,点D、E是线段BC的勾股分割点,且EC>DE≥BD,若点F是AB上的一个动点,过F作FG//BC,交AD、AE于点M、N,则M、N是否还是线段FG的勾股分割点?

设计意图:在原考题第二问的基顾上,将问题的思考从特殊到一般,学生根据相似三角形所带来的比例式,用类似的推理方式"成果扩大",获得解答.

(四)引入等边三角形,鼓励优秀学生挑战难题

问题5:(改编自考题第四问)条件呈现同"考题第四问",限于篇幅,略去.

①求证:S△ACM+S△BEN=S△DMN;

③试探究S△AMF、S△BEN和S四边形MNHG的数量关系,并说明理由.

设计意图:通过增设3个小问,把原考题的第四问中几个难点、关键点分散开来,引导学生逐个突破,实现最终问题的求解.事实上,洞察问题结构或本质看清之后,还可提出很多类似的问题,比如MN=AM;或者提问题的一些逆向思考题,比如已知AM=BN,求证:H为DN的中点等.

三、教后反思

1.深刻理解中考试题是开发"一题一课"的前提

开发"一题一课"需要考虑教学容量的问题,不少同行在复习课时为了追求所谓的教学容量,所以预设、选择了多道中考综合题,以便体现大容量的习题教学.然而这种多道综合题出现在同一节课中的教学努力常常得不偿失,突出表现在很多基础一般的学生往往跟不上教学进程,出现教师灌输、学生简单记录的低效学习,如果学生课后没有跟进消化理解,则该课几乎无效.所以开设一题一课就是要将容量降下来,但又不是单纯地减少题量这么简单,而是在教师深入理解考题的基础上让课堂内容从形式上走向简约,简约并不简单,如从上面的课例来看,增加了很多铺垫问题、变式思考、成果扩大,使得所谓例题变为一道,然而系列变式、追问却使例题生长、扩张,追求"由一题、会一类、通一片"的效果.

2."一题一课"的变式需要围绕考题主干有序展开

"一题一课"的努力就是围绕考题进行系列变式、恰当追问.然而我们也见到有些习题课堂上的变式与追问常常脱离考题的主干方向,走向旁枝末节,这是需要避免的.比如,上文中的考题的几个教学环节都针对着原考题的4个小问展开教学,而没有离开考题做其他角度的设问,这也保证了课堂主题的聚焦.这里还可提及命题领域的一个概念,即所谓"内容效度",也就是指教学目标中针对的是一道考题展开教学,而不能离开考题而开展大量的旁枝内容.比如,在一次听课中,某教师执教二次函数章末复习课,结果有大半节课在一道二次函数综合题上花时间,而这道二次函数综合题主要难点不在二次函数的图像与性质上,而是综合了平面几何的一些难点在题中,使得学生的主要困难和解题教学时间都花在几何难点上,这里就是教学内容的效度出现了问题.

1.赵萍萍."一题一课":复习课走向简约的尝试---以2014年广东省中考第23题教学为例[J].中学数学(下),2015(2).

2.罗增儒.数学解题学引论[M].西安:陕西师范大学出版社,2008.

3.鲍建生,顾泠沅,等.变式教学研究[J].数学教学, 2003(1,2,3).

4.章建跃.发挥数学的内在力量,为学生谋取长期利益[J].数学通报,2013(2).

②求证:AM=BN;