基于差分进化支持向量机的作战效能评估方法

杨健为，徐　坚，吴小役，鲁玉祥，魏继卿

(西北机电工程研究所，陕西 咸阳　712099)



基于差分进化支持向量机的作战效能评估方法

杨健为，徐坚，吴小役，鲁玉祥，魏继卿

(西北机电工程研究所，陕西 咸阳712099)

武器系统作战效能的评估具有重要意义。针对作战效能评估过程中影响因素复杂、小样本、非线性等问题，引入基于最小二乘法的支持向量机回归算法，用于作战效能的学习与预测。为了提高预测精度，引入差分进化算法进行支持向量机的参数优化选取。以地地导弹武器系统效能为例，分别采用BP神经网络算法、经典支持向量机算法与本文算法进行仿真计算，结果表明差分进化支持向量机算法可很好地实现武器系统作战效能评估，具有较好的计算精度。

作战效能；支持向量机；差分进化算法：BP神经网络

武器系统作战效能评估具有重要意义。在武器系统的设计、研制、试验、使用以及维护等过程中，效能评估都能起到指导性的作用[1]。

对武器系统进行效能评估的方法很多，传统方法有：专家调查法、试验统计法、层次分析法、解析法、指数法和SEA法等。这些方法得到了广泛应用，但存在一些问题，如受到人为因素的影响较大，武器系统的非线性被过分简化，评估指标不够体系化等，从而导致效能评估的误差增大[2]。

近年来，随着机器学习的研究不断深入，因其客观性，其在效能评估上的应用得到不断重视。而效能评估过程中，由于效能评估指标、影响因素尚未体系化、标准化，缺少效能评估的历史数据积累，对机器学习的开展造成不小难题。笔者引入差分进化支持向量机算法对武器系统的作战效能进行学习与预测，以地地导弹武器系统效能为例，在小样本的情况下，该方法可很好地完成历史数据的非线性学习，并比BP神经网络算法、传统支持向量机算法取得了更高精度的评估结果，从而有效地减小人为因素对效能评估的影响。

1　支持向量机原理

支持向量机(Support Vector Machine，SVM)是近年来机器学习、模式识别以及神经网络界最有影响力的成果之一[3]。它采用结构风险最小化原则代替传统的经验风险最小化原则，对有限样本进行学习，得到比传统统计技术和方法更好的结果。

笔者采用基于最小二乘法的支持向量机(Least Square Support Vector Machine，LS-SVM)，该方法采用最小二乘线性系统作为损失函数，替代传统支持向量机所采用的二次规划方法，可以较为客观地提高学习速度，并且在小样本情况下具备有效建模的能力和较强的泛化能力。

将已有的样本称为训练样本，可以设为X={(xi,yi)|i=1,2,…，n}，xi∈Rn，yi∈R，x、y之间存在函数关系，表现为

F={f|f∶Rn→R}

(1)

对于非线性系统，支持向量机通过非线性函数将输入空间映射到高维空间，在高维空间中得到变换后的线性规律。

f(x)=w·Φ(x)+b

(2)

式中：Φ(x)∶Rn→Rnk为输入空间映射到高维空间的非线性函数，或称为核空间映射函数；w∈Rnk为权重向量；b为偏差量。

对给定的训练样本，根据结构风险最小化原则，得到基于最小二乘法的支持向量机的优化问题：

(3)

s.t.yk=wT·Φ(xk)+b+ek,k=1,2，…，N

(4)

式中：N为训练样本容量；e为学习结果与实际结果的误差；γ为正则化参数。

为求解以上优化问题，构造拉格朗日函数，将目标函数和约束函数整合为

b+ek-yk}

(5)

式中，α为拉格朗日乘子。

根据KKT最优条件，将上式函数L对w、b、e、α求偏导数，得到：

(6)

对于i=1,2,…,N消去ei和w后，可得到如下线性方程组：

(7)

根据Mercer条件，存在核函数K(xi，xj)满足：K(xi,xj)=Φ(xi)·Φ(xj)，常用的核函数有多项式核函数、径向基函数(RBF函数)、多层感知器核函数(Sigmoid函数)。径向基函数由于可以将输入空间映射到无限维空间，是最常用的核函数之一，笔者采用径向基函数。

K(xi,xj)=exp{-(‖xi-xj‖2)/2σ2}

(8)

式中,σ为径向基函数参数。

通过对上面方程组的求解，最后得到LS-SVM的估计函数为

(9)

LS-SVM需要设置的参数为：正则化参数γ，径向基函数参数σ。参数设置对支持向量机的计算精度有着很大影响，但对于参数的设置尚缺乏比较成熟的理论证明和实践指导[4]。

2　差分进化算法

2.1差分进化算法原理

差分进化(Differential Evolution，DE)算法是模拟自然界生物种群以“优胜劣汰、适者生存”为原则的进化发展规律，而形成的一种随机启发式搜索算法。该方法采用全局搜索策略，采用实数编码、基于差分的简单变异操作，降低了遗传操作的复杂性，同时具备动态跟踪当前搜索情况的能力，可以不断调整搜索策略；具有待定参数少、不易陷入局部最优、收敛速度快等优点[5]。差分进化算法由变异、交叉和选择3个基本操作组成。

2.1.1变异操作

从群体中随机选择3个不同的个体xp1、xp2和xp3，变异得到的新的个体为hi，对当前群体通过下面变异操作得到下一进化代的个体。

hij(t+1)=xp1j(t)+F·(xp2j(t)-xp3j(t))

(10)

式中：j为对应个体的染色体序号；t为进化代数；xp2(t)-xp3(t)为差异化变量；F为变异因子。

2.1.2交叉操作

为了增加群体的多样性，在变异操作的基础上进行交叉操作，操作如下：

(11)

式中：r为[0,1]之间的随机数；CR为交叉概率，CR∈[0,1]。

2.1.3选择操作

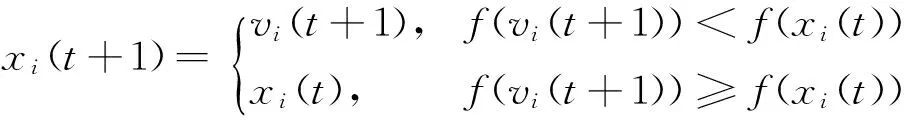
(12)

式中,f(x)为适应度函数。

进行以上3个基本步骤前，需要先生成一个初始群体，实施措施为

(13)

2.2基于差分算法的LS-SVM参数优化

支持向量机的参数选择问题可以看作一种函数寻找最优解的问题。通过大量的实践证明，学习的误差小并不意味着预测的精度高。可以通过定义合适的适应度函数，在学习精度与预测精度之间取适当的折中，作为支持向量机参数寻优的判断标准。

将样本数据集划分成训练样本集和预测样本集，再将训练样本集划分为学习样本集和验证样本集，引入交叉验证机制(Cross Validation，CV)来减小训练样本集的划分对算法的影响[6]。随机选择训练样本集中M组数据作为学习子集，剩余子集作为验证样本，建立LS-SVM回归预测模型，计算适应度函数。循环该过程K次，并记录每次循环中得到的适应度函数值；适应度函数值越小，则参数越优。定义适应度函数f如下：

(14)

式中：yi为验证样本实际值；yi′为对应的预测值；c1、c2分别为学习精度权重系数和验证精度权重系数，c1+c2=1。

3　基于差分进化支持向量机的作战效能评估

3.1基于差分进化支持向量机的作战效能评估方法

效能本质上是一个多属性函数，进行作战效能评估的首要工作是确定作战效能评估的指标体系，明确影响因素。通过试验、实际作战等积累作战效能评估经验，作为LS-SVM学习的历史数据；为了保证预测的客观性，需要尽可能避免主观因素对历史数据的干扰。

在建立了作战效能评估的学习样本库之后，根据所选择的效能评估体系，可以对数据进行归一化处理来减小数值大小对学习结果的影响，也可以进行主成分分析来适当简化学习和预测过程。

作战效能评估过程如图1所示。

3.2算例

笔者以文献[7]中地地导弹武器系统效能仿真为例说明，该效能评估方法基于贝叶斯网络的正向探索模式分析，在SIM 2000柔性仿真平台上完成，计算取得如表1所示的样本数据。取突防成功概率y作为效能指标，效能影响因素有：红外干扰诱饵释放数量X1，红外干扰诱饵释放高度X2，压制干扰机数量X3，红外导引头探测距离X4，发射距离X5。

表1　地地导弹效能评估数据样本

在仿真过程中，采用Matlab实数编码，决策变量为LS-SVM中的正则化参数γ、径向基函数参数σ。选择25个样本作为训练样本，其余4个作预测样本；训练样本集中随机选择2组作为验证样本，循环验证10次。取变异因子F=1.2，交叉因子CR=0.9，寻优参数样本个数为50，最大迭代次数G=50。一般情况下，LS-SVM正则化参数γ取值范围为(0,400)，径向基函数参数取值范围为(0.08,12)。取适应度函数中学习精度权重系数c1=0.9，验证精度权重系数c2=0.1。寻优结果为γ=400，σ=3.111 5。

为了说明基于DE的LS-SVM的预测效果，将其与传统LS-SVM算法(取γ=10，σ=1)、BP神经网络算法进行比较。BP神经网络学习在Matlab自带的神经网络工具箱中进行，采用3层神经网络，5-10-1结构，学习效率为0.05，学习规则为“trainlm”。

从训练效果与预测效果两方面对比3种算法，如表2～3所示。表2从学习样本的实际效能指标值与训练输出效能指标值的平均误差和均方差两个角度，对比3种算法的学习误差及其波动情况，反映学习效果。表3反映3种算法的预测效果，将4组待预测样本的效能指标的期望指标和预测指标进行对比，并计算预测误差。

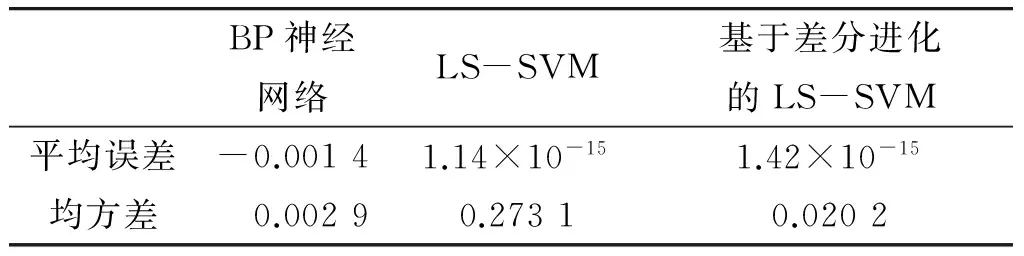
表2　3种算法的训练效果对比

表3　3种算法的预测效果对比

通过分析以上数据，得到结论如下：

1)由于样本容量较小，BP神经网络不能得到确定的学习模型，在不同的初始权值设置下，得到的训练效果和预测结果差别很大，所以在文中未做确定表示。这说明神经网络在解决小样本数据的学习问题时存在局限性，容易陷入局部次优解。

2)传统LS-SVM和DE-SVM都对小样本数据进行了确定的学习，这有效说明了支持向量机在处理小样本数据时不存在陷入局部次优解的问题。但不同的参数设置对训练效果与预测效果影响较大：2种参数的学习平均误差相差不大，但传统SVM出现了欠学习的现象，所以均方差较大；对比预测效果，DE-SVM的预测平均误差更小，说明取得了更好的预测效果。基于以上对比，说明SVM能够有效进行小样本的学习与预测，通过差分进化算法进行参数优化，能够有效提高预测效果，该方法在作战效能的评估过程中有一定的参考意义。

3)值得说明的是，历史数据对支持向量机计算结果有着重要影响，而对于武器系统的效能评估，历史数据的积累还需要更进一步的工作。

4　结束语

针对效能评估过程中影响因素复杂、小样本、非线性等问题，笔者引入基于差分进化算法和支持向量机算法的方法，用于效能评估的学习与预测。计算表明，该方法的计算结果精度较高，具有一定的可行性。

References)

[1]高尚. 基于Rough集和支持向量机的作战飞机效能评估[J]. 计算机工程，2006，32(14)：184-186.

GAO Shang. Assessing of battle plane effectiveness based on rough set and support vector machine[J]. Computer Engineer, 2006, 32(14): 184-186. (in Chinese)

[2]程恺，张宏军，柳亚婷，等. 作战效能及其评估方法研究综述[J].系统科学学报，2014，22(1)： 88-92.

CHENG Kai, ZHANG Hongjun, LIU Yating, et al. Review on operational effectiveness and evaluation method[J]. Journal of Systems Science, 2014, 22(1): 88-92. (in Chinese)

[3]史志富，雷金利，张安，等.机载火控系统效能评估的支持向量机方法[J]. 电光与控制，2010，17(3)： 9- 11.

SHI Zhifu, LEI Jinli, ZHANG An, et al. Effectiveness evaluation for airborne fire control system based on support vector machine[J]. Electronics Optics & Control, 2010, 17(3): 9-11. (in Chinese)

[4]王珏鑫. 基于多种智能计算方法的支持向量回归机参数优化[D].长春：吉林大学，2010.WANG Juexin. Parameter optimization for support vector regression based on multiple intelligent computation methods[D].Changchun:Jilin University,2010.(in Chinese)[5]刘金琨，沈晓蓉，赵龙. 系统辨识理论及MTLAB仿真[M]. 北京：电子工业出版社，2013：240-243.

LIU Jinkun, SHEN Xiaorong, ZHAO Long. The theory of system identification and MATLAB simulation[M]. Beijing: The Publishing House of Electronics Industry, 2013: 240-243. (in Chinese)

[6]唐阔，胡国胜，车喜龙，等. 基于遗传算法优化支持向量回归机的网格负载预测模型[J]. 吉林大学学报：理学版，2010，48(2)： 251-255.

TANG Kuo, HU Guosheng, CHE Xilong, et al. Grid host load prediction model of support vector regression optimized by genetic algorithm[J]. Journal of Jilin University：Science Edition, 2010, 48(2): 251-255. (in Chinese)

[7]杨峰，王维平. 武器装备作战效能仿真与评估[M]. 北京：电子工业出版社，2010： 263-264.

YANG Feng, WANG Weiping. Weapons and equipment operational effectiveness simulation and evaluation[M]. Beijing: The Publishing House of Electronics Industry, 2010: 263-264. (in Chinese)

Evaluation Method for Operational Effectiveness Based on Support Vector Machine with Differential Evolution

YANG Jianwei, XU Jian, WU Xiaoyi, LU Yuxiang, WEI Jiqing

(Northwest Institute of Mechanical & Electrical Engineering, Xianyang712099, Shaanxi, China)

It is of great significance to evaluate the operational effectiveness of weapon system. With regard to the problems such as complicated impact factors, small sample and nonlinearity, the least square support vector machine was used to study and predict the evaluation of operational effectiveness. When establishing the parameters of SVM, Differential evolution was introduced to enhance the accuracy of the prediction. With the evaluation of surface to surface missile as an example, this new method, BP neural network and traditional SVM were used for simulation calculation. It is shown that the method of LS-SVM with Differential Evolution works well for the evaluation of operational effectiveness with a better computing accuracy.

operational effectiveness; support vector machine; differential evolution; BP neural network

2015-06-02

杨健为(1992—)，男，硕士研究生，主要从事火炮总体技术研究。E-mail：yjw624@126.com

TJ01

A

1673-6524(2016)01-0016-05