模化方法在电磁轨道炮研究中的应用综述

金龙文，李　军，雷　彬

(1.军械工程学院 弹药工程系，河北 石家庄　050003；2.北京特种机电技术研究所，北京　100012)



模化方法在电磁轨道炮研究中的应用综述

金龙文1,2，李军2，雷彬1

(1.军械工程学院 弹药工程系，河北 石家庄050003；2.北京特种机电技术研究所，北京100012)

模化方法是指不直接研究自然现象或过程的本身，而是用与这些自然现象或过程相似的模型来进行研究的一种方法。选择合适的模化方法对原型与模型之间试验结果的匹配至关重要。在对模化方法进行简要介绍的基础上，对现有电磁轨道炮物理场、弹丸动力学、驱动电路模化方法的实现方式和优缺点进行了论述，探讨了当前电磁轨道炮模化方法的研究难点及未来可能的发展方向。目前尚未出现一种理想的电磁轨道炮模化方法可以同时进行所有物理量的匹配，因此，在实际应用过程中，根据具体需求选择合适的物理量和模化方法是目前较为有效的研究途径。

电磁轨道炮；发射器；模化方法；相似理论

电磁轨道炮是利用载流导体在磁场中受力的原理发射弹丸的一种新概念武器。虽然电磁轨道炮的发射原理简单，但是诸多损伤机理和部分关键问题尚未得到根本解决。例如：轨道寿命、散热控制、电磁兼容、枢轨电接触性能等。其中部分技术和相关理论取得了较大进展，而且在中小口径电磁轨道炮上得到了应用和验证，但是其研究成果是否能够外延应用到大口径电磁轨道炮上则有待进一步研究[1]。

模化方法广泛应用于工程设计与试验领域，例如飞行器的空气动力试验与结构设计、发电装置、建筑领域等。模型试验需要额外的时间和成本，但是通过试验可以预测原型中可能出现的试验现象和技术问题。通过模化方法，可以把从小尺寸低成本的模型系统上得到的研究结论，推广到全尺寸的原型系统中。

笔者在查阅文献资料的基础上，介绍了目前模化方法在电磁轨道炮研究中的应用状况，并对各电磁轨道炮模化方法的优缺点进行了论述，最后在总结全文的基础上探讨了该技术在今后的可能发展方向。

1　模化方法概述

广义的模化是指对真实事物或实物的形态、工作规律或信息传递规律在特定(一般是简化的)条件下的一种相似再现[2]。其中真实事物或实物是原型，与原型的形态、工作规律或信息传递规律相似的事物或实物是模型。

相似理论是说明自然界和工程中各种相似现象相似原理的学说，是模化方法的理论依据。它的理论基础是关于相似的3个定理[3]。在不同的文献资料中对相似定理的命名方法和顺序有所不同[2-3]，但是利用相似理论指导模型试验的基本思路是通用的。首先，应立足相似逆定理，从几何条件、物理条件、边界条件和初始条件等单值条件出发，正确、全面地确定现象的参量；其次，在确定参量基础上，通过相似正定理提示的原则建立起该现象的全部Π项(相似准则)；最后，将所得Π项按Π定理的要求组成Π关系式，以用于模型设计和模型试验结果的推广[3]。

相似准则是由数个物理量组成的一无量纲的综合数群，能反映出现象相似的数量特征，并只有在相似现象的对应点和对应时刻上相等，具有无限推广的功能[3]。相似常数是指在一对相似现象的所有对应点和对应时刻上，有关物理量的比值均保持不变的量，但是在另一对相似现象中其比值有可能会变化[3]。相似准则的导出是模化方法中的关键环节，目前相似准则的导出方法主要有：定律分析法、方程分析法和量纲分析法。其中方程分析法具有结构严密、分析过程程序明确等优点，适用于能够写出描述现象微分方程组的情况，电磁轨道炮的模化就属于此类。

2　模化方法在电磁轨道炮中的应用

2.1发射器物理场和弹丸动力学的模化

文献[4]首次以固体电枢电磁轨道炮为例，提出了一种机电系统的模化方法。该方法利用电磁场、温度场和运动方程组描述一个典型机电系统。电磁场由以下方程组描述：

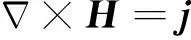
(1)

(2)

(3)

B=μH

(4)

j=σE

(5)

式中：H为磁场强度；B为磁感应强度；j为电流密度；E为电场强度；μ为磁导率；σ是电导率。

由于假设了系统尺寸远小于波长，因此忽略了位移电流项，即假设系统为磁准静态场[5]。考虑到焦耳热后，热扩散方程为

(6)

式中：T为温度；K为热导率；cp为单位体积热容。

添加电磁力分量后，运动微分方程可表示为

(7)

式中：S为应力张量；ρ为质量密度；a为加速度。

文献[4]首先从电磁场方程组导出了相似关系：为了实现模型和原型中磁感应强度B的匹配(镜像)，除了需要满足系统的几何形状相似的条件以外，时间的相似常数应与几何相似常数的平方相同，电流密度的相似常数应与几何相似常数的倒数相同。随后，把分析结果代入到温度场和运动方程后发现在上述条件下模型和原型中温度场和应力场也呈镜像分布。最后，利用EMAP3D程序，以固体电枢电磁轨道炮为例进行了静态条件下的电热耦合仿真，并把电磁力结果导入到ABAQUS软件进行了应力场分布的仿真。仿真结果显示全尺寸原型和0.707缩比模型中温度场、应力场的分布规律相似、幅值相同，验证了理论推导结果。此文献首次以固体电枢电磁轨道炮为例系统地描述了机电系统的电磁场、温度场和运动(应力场)方程，在此基础上提出了一种可匹配物理场的机电系统模化方法，为后续研究奠定了基础。但存在以下不足：在理论推导之前，就假设了模型和原型的材料相同，并未考虑材料参数的变化；在相似常数的推导过程中，首先从电磁场方程中得到了相似常数，并把结果代入到温度场和运动方程中得到了验证，因此其结果存在偶然性，在分析过程中并未严格遵守相似理论；存在的不足中最为关键的是未考虑电磁力引起的结构变化。以电磁轨道炮为例，忽略了弹丸运动引起的系统几何形状的改变。如果按照本文献的模化方法，则弹丸位移的相似常数会与初始几何相似常数不同，即随着弹丸的移动，对应时刻模型和原型的几何形状不再相似，因此更谈不上物理场相似，其结果存在错误。

文献[6]提出了线性模化方法(linearscaling)和匹配模化方法(matchingscaling)。线性模化是指模型和原型中物理场和相关变量的分布特性相同，而幅值以对应的相似常数呈比例的现象；匹配模化是指类似于文献[4]中的方法，使指定的物理场呈镜像(分布和幅值皆相同)或使指定的物理量相同的方法。文献[6]在文献[4]的多物理场方程组基础上，添加了弹丸的动力学方程和轨道表面压力方程，并通过分析得出了相似关系式。按照文献[6]的线性模化方法，将几何、弹丸质量、电流幅值和时间的相似常数作为输入相似常数，并且保证时间相似常数与几何相似常数的平方相等时，通过调整其他输入相似常数，可以实现不同比例的线性模化；而时间相似常数与几何相似常数的平方不相等时，会出现非线性现象，在一定范围内可以实现近似模化，文中最后举例验证了近似模化的情形。根据文献[6]的匹配模化方法，当时间的相似常数与几何相似常数的平方相同，且电流幅值的相似常数与几何相似常数相同时，可实现磁场、温度场和应力场的匹配；在此基础上通过改变弹丸质量的相似常数，就可分别实现弹丸加速度、速度和位移的匹配。此文献首次提出了轨道炮线性模化方法；试图同时实现发射器物理场和弹丸动力学参数的匹配；提出了时间相似常数与几何相似常数的平方不相等时的近似模化概念，并通过实例对部分弹丸动力学参数进行了验证。但存在以下不足：假设了模型和原型材料相同，并未考虑材料参数的变化；类似于文献[4]，未考虑弹丸运动引起的几何形状变化，在文献[6]的匹配模化方法中，如果匹配弹丸的动力学参数(如加速度、速度或位移)，则根据时间相似常数的特性可知，弹丸位移的相似常数与初始的几何相似常数不再相等。这时即使满足时间相似常数与几何相似常数平方相等的条件，也不能实现对应时刻原型和模型几何形状的相似，因此更不能实现物理场的匹配，此时的物理场只能是近似模化。

文献[7]在文献[4]和[6]的基础上考虑到弹丸运动的边界条件后，指出了模型和原型中当材料参数相同时，不能同时实现发射器物理场和弹丸动力学参数的匹配。而通过改变弹丸负载质量的方法，可以调整弹丸质量的相似常数，可以进一步分别实现弹丸的加速度、速度和位移的匹配，但此时由于边界条件不再相似，因此其物理场属于近似模化。作者对上述3种不同的近似模化，通过有限元仿真的方法，从能量分配、电流分布、温度分布的角度分析了近似模化的近似程度，并得出了匹配速度的近似模化最优，匹配加速度的近似模化最差的结论。文献[7]纠正了文献[4]和文献[6]中忽略边界条件的错误；把能量分配性能指标引入到了模化过程中；提出并分析了分别匹配弹丸的加速度、速度和位移的近似模化性能。其不足在于依然未考虑材料参数的变化。

总之，由于目前电磁轨道发射器物理场的模化方法只考虑了相同材料条件下的模化，因此必须满足时间相似常数与几何相似常数的平方相同的条件。在匹配弹丸动力学参数时，会进一步导致发射器长度和弹丸质量的相似常数取值过大的问题，将加大模化方法的实现难度。因此，为解决以上问题，在模化方法中考虑不同材料是可能的解决途径之一。

2.2驱动电路的模化

文献[8]提出了电容器驱动电磁轨道炮的模化方法。文章从电磁轨道炮物理场的模化方法出发，以电流、弹丸位移、时间等参数为中间变量，把物理场的模化延伸到了驱动电路的模化中。该模化方法针对类似于文献[6]中匹配弹丸加速度、速度或位移的模化方法，给出了可实现各模化方法的电路参数相似常数。此外，文中给出了电阻方程和电感方程中将弹丸位移替换为几何参数的近似模化方法，并通过数值计算的方法验证了其近似程度。该文献的意义在于首次提出了可实现电磁轨道炮物理场和弹丸动力学参数匹配的驱动电路模化方法，同时给出了电路的近似模化方法。不足点在于：该文献引用的物理场模化方法未考虑弹丸运动引起的边界条件变化，即引用的模化方法本身不能实现物理场的完全匹配。因此文献中描述的电路模化方法，即使实现了弹丸动力学参数的匹配，此时发射器的物理场也只是近似模化。

文献[9]总结和分析已发表的文献后提出了电路模化方法，并通过数值模拟的方法验证了该方法下电路参数和弹丸动力学参数的模化性能，该方法的研究思路与文献[8]类似，但在数值模拟中考虑了二极管的正向偏压等非理想条件。此外，文中给出了RLC电路试验结果，通过对设置不同的电容器初始电压的方法，分析了电路模化过程中非线性现象。最后，通过相似理论分析了轨道炮发射频率等具体工程问题。本文的意义在于，在电磁轨道炮模化过程中，考虑到了实际工程应用背景，并提出了以相似理论作为分析工具可以解释具体工程问题的可能性。

与发射器物理场的模化方法相比，驱动电路的模化相对简单。原因在于驱动电路的模化是在发射器物理场的模化方法基础上进行的，因此，一旦选择了一种发射器物理场的模化方法，则激励电流波形需要满足的条件也被确定，进一步驱动电路中电参数的相似常数随之也被确定。

2.3其他模化方法

文献[10]分析了电磁轨道炮的非线性模化方法。与之前电磁轨道炮模化方法相关文献的关注点不同，此文献重点研究了滑动摩擦、空气、电流的阻力模型以及它们在不同速度条件下的适用性。文章认为：由于摩擦系数随着滑动速度的变化而改变，因此摩擦阻力模型具有非线性特性，而且其非线性在低速段更为明显，但是在高速段可以简化到电流阻力模型中并且能够实现线性模化方法；在电磁轨道炮的发射速度范围内(尤其在低速时)，可以忽略空气阻力。本文的意义在于对比分析了不同阻力模型在不同发射阶段对弹丸动力学的影响程度，并且首次将阻力模型引入到了电磁轨道炮模化方法中。

以上文献主要是相似理论在电磁轨道炮研究中的应用情况，此外相似理论在电磁线圈炮中也有应用。文献[11]采用类似于文献[8]的方法，针对电容器驱动电磁线圈炮研究了模化方法。在电路方程、弹丸动力学方程和电磁场扩散方程组基础上获得了各物理量的相似常数，并通过试验和数值模拟的方法进行了验证。文献[12]采用类似的方法，基于新设计的电磁线圈炮基础上得到了相似常数，并利用有限元仿真进行了验证。

3　讨论

电磁轨道炮的模化，其难点在于为了满足模型与原型之间的相似性，需要同时进行多个物理场的模化，而且各物理量之间又相互关联和影响，例如：电磁轨道炮中的电磁场会产生电磁力导致结构的变形，同时产生焦耳热；结构的变形又会作为电磁场中的边界条件影响其分布特性，而电枢与轨道的相对滑动会产生摩擦热；焦耳热和摩擦热引起的温度变化又会引起材料性能的变化。因此，研究电磁轨道炮的模化方法时，不能只分析单一物理量，而应统筹考虑各参量和物理场之间的耦合关系。此外，电磁轨道炮的物理场与发射器的损伤和寿命研究息息相关，而速度作为发射类武器中最关键的技术指标之一，在电磁轨道炮中又与刨削损伤和速度趋肤效应等现象有直接联系。因此在电磁轨道炮中，需要同时进行物理场和弹丸动力学(尤其是弹丸速度)的模化。

目前电磁轨道炮的模化方法具有如下特点：

1)相似理论的推导过程只是在相似指标式或相似常数的分析层面上，并未给出真正意义上的相似准则。

2)假设了模型和原型中材料相同，限定了材料参数不变。

3)都是以匹配物理场为目标，在此基础上各方法延伸到了弹丸动力学和驱动电路等其他物理量的匹配。

4)在相同材料条件下为了实现模型和原型中物理场的匹配，时间相似常数必须与几何相似常数的平方相同。而从弹丸动力学相似性分析可以得出，为了匹配弹丸的速度，时间相似常数必须与几何相似常数相同。这是目前电磁轨道炮模化方法无法同时实现发射器物理场的精确模化和弹丸速度匹配的根本原因。

如何同时实现电磁轨道炮物理场和弹丸动力学参数的匹配是目前电磁轨道炮模化方法研究中最为迫切的任务之一。因此，基于目前常用金属材料，研究可缩比材料参数的电磁轨道炮模化方法是实现同时匹配电磁轨道炮物理场和弹丸动力学参数的可能途径之一。

4　结束语

电磁轨道炮模化方法发展至今已经取得了一定的成果，其主要研究内容涉及到发射器的物理场、弹丸动力学、驱动电路的模化。但是，目前尚未出现一种理想的电磁轨道炮模化方法可以同时进行所有物理量的匹配，各方法都有各自的取舍和平衡。因此，在设计模型实验时，首先应明确通过模型试验所要达到的目的和需要匹配的物理量，再根据具体需求选择合适的模化方法是目前较为有效的研究途径。

References)

[1]李军. 电磁轨道炮中的电流线密度与膛压[J]. 高电压技术, 2014, 40(4): 1104-1109.

LI Jun. Linear current density and bore pressure of electromagnetic railgun[J]. High Voltage Engineering, 2014, 40(4): 1104-1109. (in Chinese)

[2]李之光. 相似与模化(理论及应用)[M]. 北京: 国防工业出版社, 1982.

LI Zhiguang. Similariry and modeling (theory and application)[M]. Beijing: National Defence Industry Press, 1982. (in Chinese)

[3]徐挺. 相似方法及其应用[M]. 北京: 机械工业出版社, 1995.

XU Ting. Similarity method and its application[M]. Beijing: China Machine Press, 1995. (in Chinese)

[4]HSIEH K T，KIM B K. One kind of scaling relations on electromechanical systems[J]. IEEE Transactions on Magnetics, 1997, 33(1): 240-244.

[5]马信山, 张济世, 王平. 电磁场基础[M]. 北京: 清华大学出版社, 2011.

MA Xinshan, ZHANG Jishi，WANG Ping. Fundamentals of electromagnetic fields[M]. Beijing: Tsinghua University Press, 2011. (in Chinese)

[6]YUN H D. EM gun scaling relationships[J]. IEEE Tran-sactions on Magnetics, 1999, 35(1): 484-488.

[7]SATAPATHY S，VANICEK H. Energy partition and sca-ling issues in a railgun[J]. IEEE Transactions on Magne-tics, 2007, 43(1): 178-185.

[8]ZHANG Yadong, RUAN Jiangjun，WANG Ying. Scaling study in a capacitor-driven railgun[J]. IEEE Transactions on Plasma Seience, 2011, 39(1): 215-219.

[9]SUNG V，ODENDAAL W G.Application-based general scaling in railguns[J]. IEEE Transactions on Plasma Science, 2013, 41(3): 590-600.

[10]ZHANG Yadong,RUAN Jiangjun,LIAO Junpeng,et al. Nonlinear scaling relationships of a railgun[J].IEEE Transactions on Plasma Science,2013,41(5):1442-1447.

[11]ZHANG Yadong, WANG Ying，RUAN Jiangjun. Capacitor-driven coil-gun scaling relationships[J]. IEEE Tran-sactions on Plasma Seience, 2011, 39(1): 220-224.

[12]ZOU Bengui, LI Ruifeng, WANG Min, et al. Research on the scaling model of electromagnetic coil launcher[J]. IEEE Transactions on Plasma Science, 2013, 41(5): 1094-1099.

Review on the Application of Scaling Method to Electromagnetic Railgun

JIN Longwen1,2, LI Jun2, LEI Bin1

(1.Department of Ammunition Engineering, Ordnance Engineering College, Shijiazhuang050003, Hebei, China;2.Beijing Institute of Special Electromechanical Technology, Beijing100012, China)

Scaling method is a means by which studies are conducted on a similar model instead of a direct study of the natural phenomenon or process itself. It is important to be able to choose the appropriate scaling method to best match the results between full-scale and sub-scale experiments. On the basis of a brief introduction to scaling method, the major existent scaling methods of railgun physical fields, projectile dynamics, circuit and their relative merits are elaborated on. The current research difficulties and the potential research directions are discussed at the end of the paper. It turns out that not all quantities can be matched according to the existent nonideal scaling method. Therefore, choosing the appropriate quantities and scaling method according to the specific requirements is an effective way in practical applications.

electromagnetic railgun; launcher; modeling method; similarity theory

2015-05-13

国家自然科学基金项目(51237007,51407195)

金龙文(1987—), 男，博士研究生，主要从事电磁发射技术研究。E-mail：longwen@mail.ustc.edu.cn

TJ012.1

A

1673-6524(2016)01-0087-05