空降自行火炮着陆过程平衡肘等效疲劳寿命分析

何　健，马吉胜，吴大林，邓士杰

(军械工程学院，河北 石家庄　050003)



空降自行火炮着陆过程平衡肘等效疲劳寿命分析

何健，马吉胜，吴大林，邓士杰

(军械工程学院，河北 石家庄050003)

某空降型自行火炮着陆过程有车体姿态倾斜履带轮率先着地情况的发生，为了确定这样一次着陆冲击过程对履带系统关键部件平衡肘的损伤影响程度，建立了整炮的虚拟样机模型，通过对整炮虚拟样机模型进行空投着陆仿真以及同等路面行驶仿真，分别得到平衡肘上的动载荷谱。建立了平衡肘的有限元模型，对于着陆冲击时载荷较大的工况，采用应变疲劳分析方法ε-N进行疲劳寿命分析，对于行驶时载荷较小的工况 ，采用应力疲劳分析方法S-N进行疲劳寿命分析，通过对两种工况下平衡肘的疲劳寿命对比，计算得到这样一次着陆冲击对平衡肘的损伤影响相当于火炮在同等路面上行驶了936 km。计算结果可为火炮的可靠性评估提供依据。

固体力学；自行火炮；着陆；履带系统；疲劳寿命

自行火炮履带系统关键零部件的疲劳寿命直接影响到自行火炮任务的完成。作为空降型自行火炮，正常着陆工况下车体竖直向下，履带轮向上收起不会直接触地，然而由于火炮在空中的姿态以及地面路况等诸多不确定因素的影响，火炮在着陆时会出现履带率先着地这种情况，这对于履带系统的影响无疑是巨大的。为了确定这样的一次冲击对履带系统的寿命带来的影响，通过多次实装空投试验显然是不现实的，将耗费巨大的人力、物力和财力。随着计算机技术的快速发展，可以通过虚拟样机技术和有限元仿真技术对履带系统的关键部件进行疲劳寿命预测，从而提高分析效率[1]。

平衡肘作为履带系统连接负重轮与动力缸的关键部件，其疲劳寿命直接影响着悬挂系统的寿命。笔者针对平衡肘的疲劳寿命展开研究。基于ADAMS建立了整个空降型自行火炮的动力学仿真模型，针对自行火炮的动力学模型进行空投着陆仿真以及同样路面下的行驶仿真，分别得到平衡肘上的载荷信息。建立了平衡肘的有限元模型，通过初步的仿真发现，在着陆冲击载荷下平衡肘出现了一定的塑性应变，因此在这种工况下采用应变疲劳分析方法进行疲劳寿命分析。而后一种工况，应力较小，因此采用应力疲劳分析的方法进行寿命分析，最后通过2种工况下疲劳寿命的对比，将一次着陆冲击对履带系统的影响程度定量的转化为火炮在普通路面上行驶的里程，这样为装备的可靠性分析提供参考。整个分析流程如图1所示。

1　平衡肘动载荷的获取

1.1整炮动力学模型建立

笔者用ADAMS建立了车体和履带推进系统，以行动部分为主，用三维建模软件PROE建立了火力系统的三维模型，根据空投条件对火力系统进行了一定的简化，主要建立了炮塔、座圈、身管、炮尾、摇架和托架这几部分，将建立的三维模型导入ADAMS中，根据各个零件之间的实际运动关系添加运动副约束，并与车体完成组装，最终建立起整个自行火炮虚拟样机。履带装置分为两侧，每侧由1个主动轮前置牵引履带运动，5个负重轮支撑车体重量，3个托带轮分布支撑上支履带，1个诱导轮后置规正履带运动方向；履带子系统由96块履带板和96根履带销组成，用来将主动轮的扭矩变为牵引力，并增大自行火炮的着地面积和附着力，为车辆提供行驶轨道。

平衡肘与车体之间的约束关系，通过一个转动铰链和双向力矩来描述，根据油气悬挂的特点，双向力矩的非线性主要来自气体的多变指数。假设，作用缸活塞产生s的位移，则产生的作用力为

(1)

式中：P0为初压；A1、A2分别为作用缸和蓄压器的有效作用面积； s0为蓄压器中气体初始长度；m为气体多变指数；c为阻尼。前一项为刚度项，后一项为阻尼项。

将该力等效为平衡肘端点的扭矩，以样条函数的形式进行加载，通过比较火炮在静平衡状态下的负重轮所受的静载荷与设计说明书上的数值，验证了平衡肘模型的有效性，数值对比结果如表1所示。

表1　静平衡时负重轮受力对比　N

最终建立的整个自行火炮虚拟样机如图2所示。共有257个单体组成，1 194个自由度。

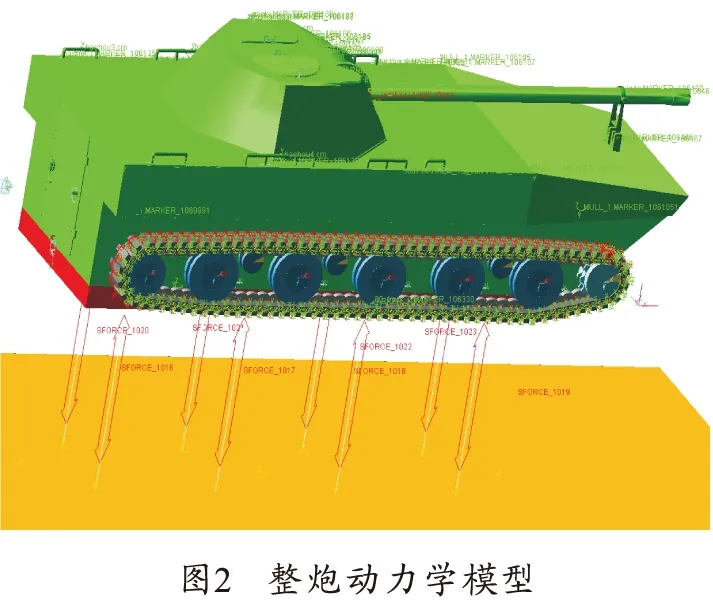
1.2动力学仿真获取载荷

在空投时，由于负重轮位移可能较大会击穿油气悬挂，所以空投时放掉了悬挂中的油液，此时油气悬挂的刚度系数和阻尼系数取0，构件之间的约束关系为接触-碰撞，火炮在行驶时，油气悬挂刚度系数和阻尼系数按照式(1)计算得到的数值。

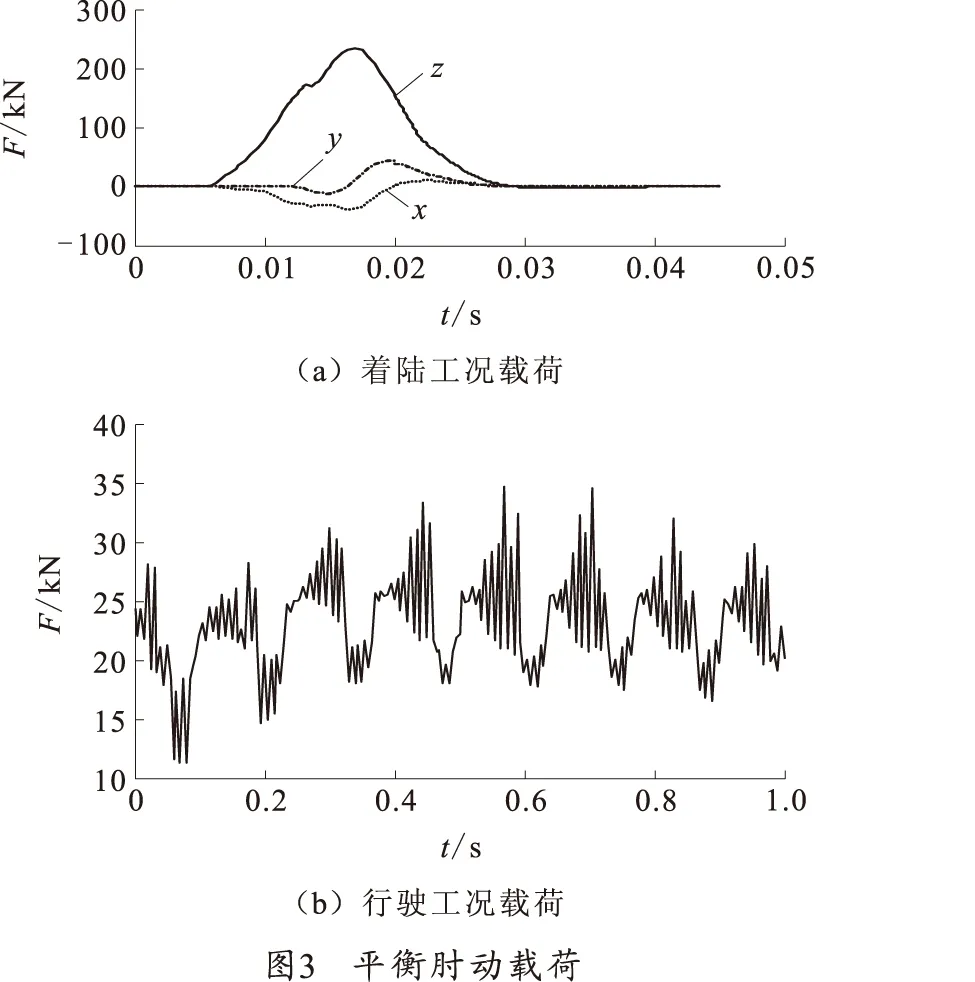
车体姿态倾斜10°，左侧履带系统率先触地，着陆地面为软土地面，着陆速度为8 m/s，对整炮动力学模型进行着陆仿真，得到着陆冲击过程左侧履带系统第2负重轮上的平衡肘与负重轮连接端上的力载荷最大，3个方向上的分力载荷如图3(a)所示。

对车体在同样的普通A级路面上进行行驶仿真，行驶速度为36 km/h，仿真时间为1 s，得到第5负重轮上的平衡肘与负重轮连接端的力载荷最大，合力载荷如图3(b)所示。

2　行驶工况下应力疲劳预估

当疲劳载荷相对较小，不会使材料产生宏观塑性变形时，也就是在高周疲劳下，一般采用应力疲劳分析方法进行寿命预估[2]。

2.1材料S-N曲线

应力疲劳分析的基础是材料的S-N曲线，S-N曲线描述了作用应力S与结构破坏时的寿命N之间的关系。S-N曲线最常用的数学表达形式是幂函数式[3]，即

SaN=C

(2)

式中，a与C是与材料、应力比、加载方式等有关的参数。

对式(2)两边取对数，有

lgS=A+BlgN

(3)

式中:材料参数A=lgC/a;B=-1/a。式(3)表示应力S与寿命N间有对数线性关系。

平衡肘所选用的材料是国产钛合金Tc10，弹性模量为113GPa，泊松比为0.3，屈服强度为860MPa，抗拉强度为980MPa，最终在Fatigue软件中形成的材料S-N曲线如图4所示。

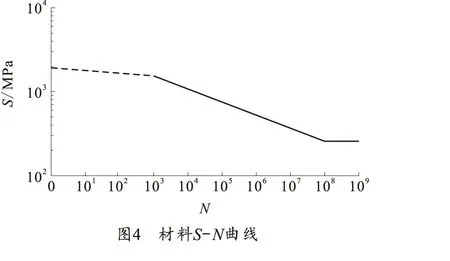
对平衡肘进行寿命估算，还需要考虑零件加工工艺、尺寸和结构形状等多方面因素，在计算过程中一般采用系数修正的方法，包括有效应力集中系数、尺寸系数和零件表面状况系数等。这里由于平衡肘的过渡段圆弧比较大，所以不考虑应力集中对疲劳寿命的影响，取有效应力集中系数为1，根据平衡肘的直径，通过查手册得到零件的尺寸系数为0.76，平衡肘在加工过程中经过热处理，取强化系数为1.05。

2.2平均应力修正和疲劳累积理论

材料的S-N曲线是在给定的应力比R=-1下得到的，但实际结构一般服从随机变幅载荷，大量研究表明，应力历程中的平均应力对疲劳寿命有较大的影响，拉伸平均应力会缩短疲劳寿命，压缩平均应力可以增加疲劳寿命。

工程中经常使用的是Goodman应力修正，用一个等效的零平均应力去修正实际应力幅值，等寿命下的循环应力幅Sa与平均应力Sm的关系可用下式描述[4]：

Sa=S-1(1-Sm/Su)

(4)

式中：S-1为材料在应力比R=-1下的疲劳极限；Su为材料的极限强度。

线性累积损伤理论Miner理论是工程上广泛采用的疲劳寿命计算方法，若构件在某恒应力水平S作用下，循环至破坏的寿命为N，则可定义其在经受n次循环时的损伤为

D=n/N

(5)

构件在应力水平Si作用下，经受ni次循环损伤为Di=ni/Ni，破坏准则为D=1。若在k个应力水平Si作用下，各经受ni次循环，则可定义其总损伤为

(6)

2.3行驶工况下平衡肘的寿命预估

首先通过有限元前处理软件Patran对平衡肘进行有限元建模，网格采取四面体自由网格形式划分，材料模型为各向同性弹塑性材料，最终形成的平衡肘有限元模型如图5所示。

利用Nastran求解器对平衡肘的有限元模型进行单位载荷下的静力学求解，得到单位载荷下平衡肘的Von Mises应力响应情况如图6所示，从图6中可以看出，平衡肘的应力比较大的区域位于平衡肘的根部，单位载荷下11 417节点的最大应力达到了0.01 MPa。

将有限元分析的结果导入Fatigue软件中，并且将图3(b)中的载荷工况以DAC文件的方式导入Fatigue软件中，将有限元分析工况与平衡肘的实际动载荷时间历程相关联，对平衡肘进行应力疲劳寿命分析，最终得到行驶工况下平衡肘根部的寿命云图如图7所示。

从图7中可以看出，在经历3.22×107次载荷循环之后，平衡肘的根部会失效，由于每次载荷循环时间为1 s，而火炮的行驶速度为36 km/h，一次载荷循环相当于火炮行驶了10 m，所以平衡肘的寿命为火炮行驶里程322 000 km。

3　着陆工况下应变疲劳预估

当疲劳载荷相对较大，材料产生了塑性变形时，也就是低周疲劳下，采用应变疲劳分析方法是比较恰当的。

3.1材料的本构模型

对于常用金属材料，通常可用Ramberg-Osgood弹塑性应力-应变关系对材料的本构关系进行描述[5]：

(7)

式中：εe、εp分别为弹性应变和塑性应变；σ为应力；E为材料的弹性模量；K为强度系数,具有应力量纲;p为应变硬化指数，无量纲，常见金属材料的应变硬化指数一般在0～0.6之间。

式(7)是反应弹塑性材料本构关系的非线性模型，考虑到火炮着陆过程冲击加速度较低，应变率强化效果不明显，且材料温度为室温，可以不考虑温度影响，因此仅考虑材料的应变强化效应。

在计算平衡肘的循环应力应变响应分布时，将式(7)的强度系数K和应变硬化指数p改为循环强度系数K′和循环应变硬化指数p′即可。常见金属材料的循环应变硬化指数在0.1～0.2之间。

3.2材料的应变寿命关系

应变寿命曲线，描述的是应变与寿命之间的关系，用ε-N曲线来描述。在研究低周疲劳时，Manson-Coffin给出了塑性应变与失效循环数的关系表达式[6-7]：

(8)

式(7)、(8)中的6个参数是表征低周疲劳特性的主要参数，为了得到这些参数，需要做大量的疲劳试验，这需要消耗大量的试件和时间，目前工程上可采用估算的方法得到这些参数[8]。

(9)

于是钛合金Tc10材料的疲劳参数计算如表2所示。最终得到的材料的循环应力-应变曲线和应变寿命曲线分别如图8、9所示。

表2　Tc10应变疲劳参数

3.3着陆工况下平衡肘的寿命预估

将有限元分析的结果导入Fatigue软件中，并且将图3(a)中的载荷工况以DAC文件的方式导入Fatigue软件中，将有限元分析工况与平衡肘的实际动载荷时间历程相关联，对平衡肘进行应变疲劳分析，最终得到着陆工况下平衡肘的寿命云图如图10所示。

从图10中可以看出，在经历344次载荷循环之后，平衡肘发生了局部失效。

4　结论

1)在火炮倾斜着陆履带系统触地工况下，平衡肘经历344次载荷循环后会出现局部失效，而在同样的路面上行驶，火炮可行驶322 000 km后会出现平衡肘局部失效，这样可以直观地将这样一次着陆冲击对履带系统的影响等效为火炮在同样的路面上行驶了936 km，研究结果可为火炮的可靠性评估提供参考。

2)在对平衡肘进行有限元分析时，发现平衡肘的根部出现了应力集中，这可以为平衡肘的局部结构加强或结构改进提供依据。

References)

[1]王红岩，芮强．履带车辆悬挂系统关键部件疲劳寿命预测技术研究[J]．装甲兵工程学院学报，2006，20(1)：44-47.

WANG Hongyan，RUI Qiang．Study on fatigue life prediction of the key parts of tracked vhicles suspension system[J]．Journal of Academy of Armored Force Engineering，2006，20(1)：44-47.(in Chinese)

[2]阿合买提江·买买提．金属材料应变疲劳寿命的估算[J]．中国稀土学报，2005，23(增刊2)：201-205.

Ahmatjiang Mamat．Estimation for strain-tired life of metallic materials[J]．Journal of the Chinese Rare Earth Society，2005，23(Sup2)：201-205.(in Chinese)

[3]王国军．Msc.Fatigue疲劳分析实例指导教程[M]．北京：机械工业出版社，2009：10-15.

WANG Guojun．Msc.Fatigue analysis example tutorial[M]．Beijing：China Machine Press，2009：10-15.(in Chinese)

[4]缪炳荣．基于多体动力学和有限元法的机车车体结构疲劳仿真研究[D]．成都：西南交通大学，2006.

MIAO Bingrong．Simulation research of locomotive carbody structure fatigue based on multi-body dynanics and finite element method[D]．Chengdu：Southwest Jiaotong University，2006.(in Chinese)

[5]王灵卉，李志谭，刘渭祈．铸造锌铝合金ZA27的应变疲劳特性[J]．铸造设备研究，1998(4)：27-37.

WANG Linghui，LI Zhitan，LIU Weiqi.The cycle fatigue properties of alloy ZA27[J]．Research Studies on Foundry Equipment，1998(4)：27-37.(in Chinese)

[6]安江英，梁双印，张保衡．三参数应变疲劳公式的研究[J]．华北电力大学学报，1997，24(1)：47-51.

AN Jiangying，LIANG Shuangyin，ZHANG Baoheng．A study of three-parameter strain fatigue formulation[J]．Journal of North China Electric Power University，1997，24(1)：47-51.(in Chinese)

[7]郑飞，何玉怀，苏彬．低周疲劳寿命预测模型分析[J]．实验室研究与探索，2007，26(10)：189-192.

ZHENG Fei，HE Yuhuai，SU Bin．Analysis of low cycle fatigue life prediction models[J]．Research and Exploration in Laboratory，2007，26(10)：189-192.(in Chinese)

[8]徐鹏，姚卫星．估计金属材料应变疲劳性能参数的新方法[J]．江苏航空，2011(增刊1)：19-22.

XU Peng，YAO Weixing．A new method of estimation of strain fatigue material performance parameter[J]. Jiangsu Airlines，2011(Sup1)：19-22.(in Chinese)

The Analysis of Equivalent Fatigue Life of the Balance Elbow for the Landing Impact Process of an Airborne of Self-mechanized Gun

HE Jian, MA Jisheng, WU Dalin, DENG Shijie

(Ordnance Engineering Colleague, Shijiazhuang050003, Hebei, China)

It happens that the track system of a certain airborne type of self-mechanized gun can first touch the groud at the landing process owing to the tilt of the hull. In order to determine the degree of damage of the balance elbow, a key part of the track system in this process, the dynamic model of the gun was built. Then the landing simulation and driving simulation to the gun model were conducted respectively, getting the dynamic load spectrum on the balance elbow. With the finite element model of the balance elbow built, strain fatigue life analysis method is used for the large load at the landing condition; stress fatigue life method is used for the small load at the driving condition. Through a comparison of the fatigue life of the balance elbow in the two conditions, it is worked out that the damage effect of such landing on the balance elbow is equivalent to the gun’s running 936 kilometer on the same road. The calculation results can provide basis for the reliability evaluation of the gun.

solid mechanics; self-mechanized gun; landing; track system; fatigue life

2015-03-02

何健(1991—)，男，硕士研究生，主要从事多体系统动力学仿真技术研究。E-mail：hejian108@163.com

TJ818

A

1673-6524(2016)01-0074-05