基于Fluent的并联操作压缩机汇流管道模型设计
王家祥,魏焕景,马 江(航天长征化学工程股份有限公司 兰州分公司,甘肃 兰州 730010)
基于Fluent的并联操作压缩机汇流管道模型设计
王家祥,魏焕景,马江
(航天长征化学工程股份有限公司 兰州分公司,甘肃 兰州 730010)
针对某项目CO2压缩单元并联操作压缩机出口汇流管道的设计问题,本文利用Fluent软件模拟汇流管道模型,研究在T型三通前增加偏心异径管、同心异径管和支管气流不同入射角度的两种情况下,分析气体混流前后的压力、速度和主管中心能量等参数的变化。计算结果表明:T型三通前增加偏心异径管汇流后的主管气流对下管壁的冲刷非常大,同心异径管汇流后的主管中心能量波动小;支管Inlet2入射角为45°时速度梯度在管道中间处最大,主管中心能量波动最小,管道内流型最为稳定,气流对管道上下管壁的影响非常小,故45°为最佳入射角。
汇流;三通;压缩机;并联操作
某项目CO2压缩单元的作用是将脱硫脱碳装置送过来的CO2进行加压,以达到气化输煤系统所需要的压力。CO2压缩机为往复式压缩机,压缩机由电机驱动,压缩机共4台(三开一备),共经过四段压缩后的CO2气体压力为8.0MPa(G),经外管网送至气化单元输送煤粉用。本文以此项目压缩机出口的汇流管道布置为依据,建立管道汇流模型,通过GAMBIT建模以及FLUENT分析,比较了几种管道布置方式的优缺点,为管道布置提供理论依据。主要研究内容有以下两个方面:
(1)对并联操作压缩机汇流管道进行模拟分析。首先模拟在T型三通前增加偏心异径、同心异径管,分析对比两种情况下的压力、流速、主管中心能量的变化,从而为筛选最优的异径管提供依据;
(2)通过模拟支管气流的不同入射角度,来判断流型变化和混流的效果,进而提出最优的支管汇流方式。
1.1计算模型的确定与简化
多台压缩机并联工作时,每台压缩机排出支管与总管合流时,应从总管顶部引入或按顺流方向成45°斜接[1],所以本文先对汇流管道的基本管件T形管和特殊三通进行几何模型的确定,特殊管件图见图1。

图1 汇流模型中的特殊管件图Fig.1 Special fittings in confluence model
几何模型采用汇流管道的二维平面模型,管道考虑绝热条件,支管管道管径为80mm,主管管径为200mm。由于项目设计的实际情况,第三个支管汇流发生在第二个支管15m的位置,其入口方式和介质参数与第二个支管相同,为了简化模拟,我们只取支管Inlet2汇流后5m内管段进行研究,几何模型见图2。

图2 汇流模型的几何参数Fig.2 Geometric parameters of confluence model
实际上,汇流管道的流动情况比较复杂,即使在边界条件不变的情况下,流体在管内的流动过程中参数并不是恒定的,为了保证模拟结果的真实性,我们还需要引入K-ε湍流方程。标准K-ε湍流模型假定流场是完全发展的湍流,忽略了流体分子之间的粘性。其中湍流动能方程(K方程)是精确方程,耗散方程(ε方程)是经验公式推导出来的方程[2,3]。
湍流动能方程(K方程):

耗散方程(ε方程):
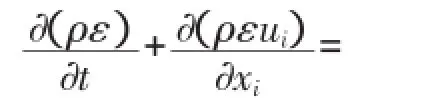
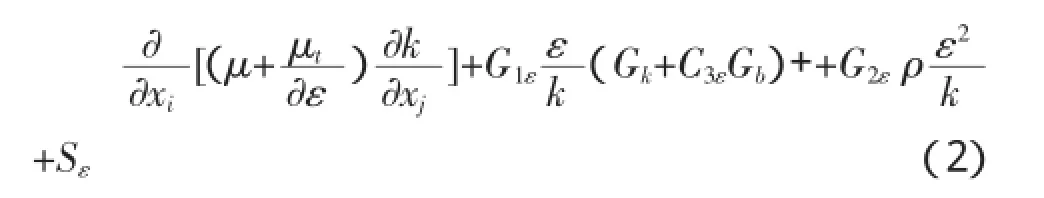
式中k:湍流动能;ε:扩散动能;ρ:流体密度,kg·m-3;u:流体速度,m·s-1;μ:湍流粘度;σk、σε-K方程和ε方程的湍流Pr数,一般取1.0,1.3;Sk、Sε:自定义选项;C1ε、C2ε、C3ε:常数,一般取1.44、1.92和0.09。
1.2GAMBIT网络模型
(1)确定求解器选择用于CFD计算的求解器为FLUENT5/6。
(2)创建汇流管模型及划分网格按照图2的几何参数绘制出汇流管的二维参数模型,考虑到计算的精确性,同时又能使计算时间比较短,通过多次的尝试之后,决定对不段区域采用不同的网格尺寸。
(3)定义边界类型在该模型中的边界类型有四种:进口 1、2(Inlet1、2)、出口(Outlet)、管壁(Wall)。
(4)输出网格文件选择File/Export/Mesh,输入文件的路径和名称。
1.3求解模型[4]
(1)控制方程和离散格式利用FLUENT软件进行数值模拟。求解的条件采用非耦合求解法(Segregated)、隐式算法(Implicit)、二维空间(2D)、定常流动(Steady)、绝对速度(Absolute),选用标准K-ε湍流模型,近壁节点采用标准壁面函数法处理。采用SIMPLE算法处理压力-速度耦合,动量采用二阶迎风格式离散,其他物理量采用一阶迎风格式离散。
(2)定义边界条件设置流体材料属性(该计算中为气体CO2,工作压力8.0MPa,工作温度405K,密度120.84kg·m-3,粘度0.02cp)。此外,还可以建立控制方程组的边界条件:
①汇流管道两个支管入口的压力和温度;
②管道的热边界条件(一般处理为绝热);
③汇流管出口的压力及温度;
(3)设置监视器及迭代计算。
2 结果与讨论
2.1理想条件下的T形三通前不同异径管汇流的模拟结果
2.1.1计算模型的选取
模拟参数:两支管Inlet1、Inlet2入口压力相等均为8.0MPa,流体温度相等均为405K,出口压力为7.992MPa。迭代计算收敛后其结果如下。
2.1.2计算结果分析

图3 压力分布图Fig.3 Pressure profile

图4 速度分布Fig.4 Velocity profile
从图3~4中可以看出,T型三通前增加同心异径和偏心异径管汇流模型压力大的区域主要集中在两股气流交汇的前方区域,可能的原因是支管Inlet2以垂直于支管Inlet1的角度进入总管,造成交汇前端一定程度的气阻,从而压力增大;两支管气流交汇后,汇合后的主管气流对下管壁的冲刷非常大,其速度梯度最大的区域集中在下管壁处,但是偏心异径管汇流的主管气流在下管壁处的速度梯度明显较大,且支管气流相交的前方夹角区域内形成了明显的涡流。随着距离的增长,同心异径管汇流较偏心异径管汇流先趋于稳定,压力梯度越来越小。
定义主管中心处的能量为H[5]:

由图5可知,T型三通前增加同心异径和偏心异径管汇流模型的H-L变化趋势基本一致。在第一阶段L<0.5m时,高压CO2气体从Inlet1口进入,气流比较缓和;在第二阶段0.5m<L<0.8m时,气体进入异径扩大管,速度明显减小;在第三阶段0.8m<L<2.0m时,两股气流进行交汇,在1.0m处速度快速达到最大,随后较快速衰减;在第四阶段2.0m<L<5.0m时,气流速度逐渐趋于稳定,流型稳定。由于偏心异径管汇流后的主管气流靠近下管壁的速度梯度较大,所以其主管中心处的能量较同心异径管低,这与图4的速度分布也是一致的。其次,同心异径管汇流的主管中心能量在4个阶段中波动较小,因此管道所受到的冲击力小,管道内流型最为稳定。所以,气体汇流时在T形三通前我们应优先选择选用同心异径管。
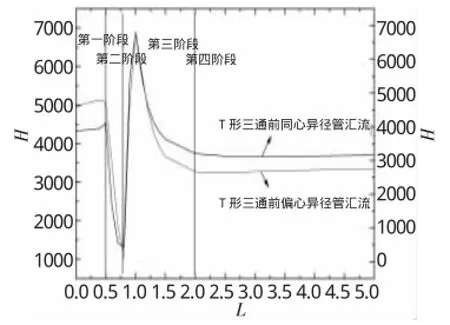
图5 H-L变化曲线Fig.5 The H-L curve
2.2Inlet2支管斜接角度的选取
压力管道布置中,往往要求管道有一定的柔性,必要时需在支撑点选用不同类型的支架来保持其受力平衡,从而尽量使管道受到的冲击力小,管道内流型稳定[6,7]。针对压缩机支管与总管合流时,支管应从总管顶部引入或顺流方向斜接这一原则,根据2.1的结论,本研究在三通前选取同心异径管进行汇流,探讨不同入射角度对汇流模型的影响,为优化管道布置提供流体力学上的参考。
2.2.1计算模型的选取
模拟参数:两支管Inlet1、Inlet2入口压力相等均为8.0MPa,流体温度相等均为405K,出口压力为7.992MPa,支管Inlet2的入射角度分别选取30°、45°、60°、90°。迭代计算收敛后其结果如下。
2.2.2计算结果分析

(a)入射角度为30°的压力分布

(b)入射角度为45°的压力分布

(c)入射角度为60°的压力分布

(d)入射角度为90°的压力分布图6 压力分布Fig.6 Pressure profile

(a)入射角度为30°的速度分布

(b)入射角度为45°的速度分布

(c)入射角度为60°的速度分布

(d)入射角度为90°的速度分布图7 速度分布Fig.7 Velocity profile
从图6中可以看出,随着支管Inlet2入射角度的增大,汇流后的主管压力重心逐渐从右往左偏移,30°时主管压力主要集中在上管壁处,90°时压力在下管壁处达到最大,60°时在两股气流交汇处前端的压力较大,而在45°时,主管压力集中在管中心,对上下管壁处的影响较小。这一结论与图7相对应,即两股气流汇流后,随着支管Inlet2入射角度的增大,主管速度梯度逐渐从上往下偏移,30°时速度梯度在上管壁处达到最大,90°时速度梯度在下管壁处最大,60°时速度梯度主要集中在下管壁处,而在45°时速度梯度在管道中间处最大。

(a)入射角度为30°的K值

(b)入射角度为45°的K值

(c)入射角度为60°的K值

(d)入射角度为90°的K值图8 不同入射角对应的K值Fig.8K value of different angle
湍流参数K值的分布云图见图8。如图所示,两股气流交汇的前后端都存在漩涡。随着支管Inlet2入射角度的增大,支管Inlet2前端的漩涡逐渐减小,但是支管Inlet2后端的漩涡会随着入射角的增大而增大。而入射角为45°时,两股气流交汇所产生的漩涡最小,且湍流参数K值也是最先稳定下来;30°次之;60°衰减之后还有起伏;而90°时,湍流参数最不稳定,其衰减距离最远。

图9 不同入射角的H-L变化曲线Fig.9 H-L curve of different angle
从图9中可知,支管Inlet2不同入射角汇流模型的H-L变化趋势基本一致,但是每个阶段的不同入射角变化幅度较大。在第一阶段L<0.5m时,高压CO2气体从支管Inlet1进入,30°入射角对应的主管中心能量明显大于其它入射角的主管中心能量,45°与60°相差无几,90°最小,可能的原因随着入射角度的增加,支管Inlet2对支管Inlet1的影响越大,导致支管Inlet2气流不能很顺畅的进入主管,造成一定程度的气阻,从而速度明显减小,相应的主管中心能量减小;在第二阶段0.5m<L<0.8m时,气体进入异径扩大管,气体流速减小,所有主管中心能量出现明显减小;在第三阶段0.8m<L<2.0m时,两股气流进行交汇,在1.0m处所有主管中心能量达到最大,随后较快速衰减。其中,在两股气流交汇处,90°入射角对应的主管中心能量最大,60°次之,45°再次之,30°最小。说明90°入射角交汇处由于两股气流的相互撞击产生巨大的能量,而30°入射角由于基本与主管平行,所以气流之间很容易混合在一起,速度变化更为平顺,所以其在这个阶段波动最小;在第四阶段2.0m<L<5.0m时,气流速度逐渐趋于稳定,流型稳定。我们发现主管能量排序:30°>60°>45°>90°,对于工业管道而言,管道元件都要安装在流型稳定处,因此,第四阶段最适合管道元件的安装。但是,我们发现入射角为45°时,主管中心能量在4个阶段中波动最小,因此,管道所受到的冲击力小,管道内流型最为稳定,从这个角度而言,45°也为最佳入射角,这与图6~8得出的结论也是一致的。即当入射角为45°时,混流长度越短,流型稳定的越快,对上下管壁的冲刷越小,因此,45°才是最佳入射角。
3 结论
在对并联操作压缩机汇流管道进行流体特性分析的基础上,从设计思路出发,筛选出在T型三通前合理的异径管和支管斜接的最佳入射角度,为今后压缩机并联汇流管道的设计提供流体力学数据上的一种参考。主要结论如下:
(1)T形三通前宜选择同心异径管进行汇流。偏心异径管的主管支流对下管壁的冲刷非常大,同心异径管汇流的主管中心能量波动小,流型稳定;
(2)支管宜从总管顶部斜接,45°为最佳入射角。入射角为45°时速度梯度在管道中间处最大,主管中心能量波动最小,管道内流型最为稳定,对管道上下管壁的影响非常小,故45°也为最佳入射角。
(3)根据本研究得出的结论优化管道布置,通过选取异径管和支管角度的组合,可以最大限度的减小流体汇流对管道的冲刷破坏作用,使管道流型稳定,便于后续管件的安装。
[1]章日让.石化工艺及系统设计实用技术问答(第2版)[M].北京:中国石化出版社,2007.
[2]任志安,郝点,谢红杰.几种湍流模型及其在FLUENT中的应用[J].化工装备技术,2009,30(2):38-44.
[3]杨康,刘吉普,马雯波.基于FLUENT软件的T型三通管湍流数值模拟[J].化工装备技术,2008,29(4):33-36.
[4]韩占忠,王敬,兰小平.FLUENT流体工程仿真计算实例与应用[M].北京:北京理工大学出版社,2004.
[5]邹杰.基于FLUENT的三通内流体流场模拟分析研究[D].上海:华东理工大学,硕士论文,2014.
[6]范开智.配管设计中简单应力管线的柔性分析[J].大氮肥,2015, 38(3):200-216.
[7]李雪晶.浅析压力管道应力分析[J].纯碱工业,2016,1:34-36.
Confluence modeling design on parallel process of compressor based on CFD Code FLUENT
WANG Jia-xiang,WEI Huan-jing,MA Jiang
(Changzheng Engineering Co.,LTD Lanzhou Branch,Lanzhou 730010,China)
According to the design of the outlet pipe of the compressor in parallel operation for a certain project,the Fluent software was used to simulate the pipeline model in this paper.In the study of arrangement of eccentric different diameter pipe,concentric different diameter pipe before tee and the different branch airflow with different angle in two cases,the pressure,velocity and the energy of the center of the gas flow were analysed.The results show that the erosion of the lower pipe wall by the head of the eccentric different diameter pipe was very large,while the energy fluctuation was small in the center of the concentric different diameter.When the incident angle was 45 degrees,the velocity gradient was the largest in the middle of the pipe,meanwhile the energy fluctuation was the least,and the flow pattern was the most stable in the pipeline,the influence on the pipe wall was very small,so the 45 degree was the best incident angle.
confluence;tee;compressor;parallel process
TQ018
A
10.16247/j.cnki.23-1171/tq.20160821
2016-06-20
王家祥(1988-),男,汉族,助理工程师,2014年毕业于西安石油大学化学工艺专业,硕士研究生,从事工艺设计和研发工作。
1建立模型和参数设定

