基于SPH方法的铸造充型过程数值研究

周学君，陈　丁

(1. 黄冈师范学院 数理学院，湖北 黄州 438000；2. 河海大学 力学与材料学院，江苏 南京 210098)



基于SPH方法的铸造充型过程数值研究

周学君1,2，陈丁2

(1. 黄冈师范学院 数理学院，湖北 黄州 438000；2. 河海大学 力学与材料学院，江苏 南京 210098)

数值方法模拟铸造充型过程一直是铸造学科的研究热点，考虑利用光滑粒子流体动力学(Smoothed Particle Hydrodynamics，SPH)方法研究铸造充型过程。SPH方法是一种成熟的无网格粒子数值计算方法，特别适合模拟大变形问题。在建立充型过程的计算模型的基础之上，通过弓形件和环形件两个充型的水模拟算例，并与实验和文献中结果比较，展示了本文SPH算法在处理铸造充型问题中的优势。

光滑粒子流体动力学；铸造充型；无网格；数值模拟

铸造是基础工业中重要的工艺方法，它利用液态金属的流动性，在特定形状的铸模的约束下，把金属材料制造成各种用途的铸件。充型过程是铸件成型的第一个阶段，过程中伴随着一系列的复杂的物理和化学变化，易发生铸件缺陷对铸件的产品质量产生重要影响；特别是在充型过程中，型腔始终是密闭状态，很难直接观测金属流在型腔内的运动规律。数值模拟为铸造充型过程的研究提供了一种方便廉价的思路，不仅可以帮助工程师直接观察到金属流在型腔内的流动状态，而且再现性好，缩短产品开发周期和降低成本。

铸造充型过程的模拟是通过求解一系列的守恒方程，得出腔内流体的运动规律；主要困难在于守恒方程中压力的计算和自由表面的位置、形状的判断。自上世纪60年代开始，人们开始利用数值方法来模拟铸造充型过程，大多是基于网格类方法。针对守恒方程中压力场的计算，出现了SIMPLE方法(1972)[1]和PISO 方法(1986)[2]等；针对自由表面的追踪方面，提出了MAC方法(1965)[3]，VOF方法(1981)[4]，PIC方法(1987)[5]和Level Set方法(1988)[6]等。以这些方法为基础，人们也开发一些铸造充型过程的仿真和分析的商业软件，如Magmasoft，Flow3d，A DSTEFAN，A nycasting，华铸 CAE，FT-STAR等。众所周知，基于网格的数值方法在处理极度大变形问题时，会出现因网格扭曲或者缠绕而引发的计算精度降低和失败等情况。无网格方法摆脱了网格的限制，在处理大变形、自由表面、运动交界面等网格类算法难以解决的问题时，展现了独特的优势。

光滑粒子流体动力学是目前发展最成熟的无网格方法之一，是由Lucy(1977)[7]、Gingold和Monaghan(1977)[8]并行提出的一种Lagrangian形式的无网格粒子计算方法。SPH方法最初用于解决天体物理学相关问题，而后被广泛应用于流体力学和固体力学的诸多领域。在SPH方法中，将求解域离散成一系列粒子，粒子间通过核函数来建立相互作用，对于自由表面的追踪能够通过粒子的位置自动确定，从而方便地获取充型过程中流体的流动轨迹，在铸造充型过程模拟中具有很大优势。曹文炅在其博士学位论文[9]较系统地阐述了SPH方法在铸造充型中的应用；强洪夫等[10]采用罚函数来处理流体与壁面之间的作用，对水模拟充型过程进行SPH数值分析。

本文以铸造充型水模拟模型为算例，并与相关文献和实验结果比较，研究该SPH算法在充型仿真中的可靠性。

1　SPH方法的近似和控制方程的离散

1.1SPH方法的近似

在SPH方法中，将连续体离散成有限个粒子，通过对某个粒子的支持域内其他粒子的加权求和获得该点的数值解。SPH方法近似分两步进行，第一步是积分近似；第二步是粒子近似。

场函数f(x)在问题域Ω内的积分近似表示式为

(1)

式(1)中x，x′为包含在问题域Ω内点的坐标向量；dx′表示x处无穷小体元；h是光滑长度；W为光滑函数(核函数)，这里采用三次样条函数[11]为光滑函数。

积分表示式(1)可写成离散化的粒子近似式：

(2)

这里mj，ρj分别表示粒子j的质量和密度，j=1,2,…，N,N为在x处粒子的支持域内的粒子总数。

于是，在粒子i处的场函数的粒子近似式可写成

(3)

其中Wij=W(xi-xj,h)，且f(x)的导数的粒子近似式为

(4)

1.2控制方程的SPH离散

Lagrangian描述下的流体动力学控制方程包括连续性方程、动量方程和运动方程：

(5)

(6)

(7)

其中α表示Cartesian坐标分量x,y和z，重复下标代表Einstein求和法则；ρ，v，p分别为密度、速度和压力；g是体力；D/Dt代表物质导数。另外，本文研究水模拟铸造充型问题，故压力p是由弱可压缩流体的状态方程[12]得出：

(8)

式中ρ0取流体初始密度，参数γ取7，且参数B由

(9)

确定，其中vmax为流体的最大速度。

将上述流体控制方程应用SPH核近似和粒子近似后，离散化的SPH公式为

(10)

(11)

(12)

这里式(11)和(12)中包含对称结构，可以减少由于粒子不一致问题产生的误差[13]，而文献[9]中采用移动最小二乘法来处理此问题；另外，式(11)中Πij为人工粘度项，它的作用是消除SPH方法在模拟流体动力学问题时产生的数值不稳定性，本文采用的人工粘度[14]为

(13)

其中

(14)

式中αΠ和βΠ是常数，取1.0左右； c为声速，为保证流体的弱可压缩性，本文取c=10vmax；vij=vi-vj，xij=xi-xj。

1.3边界条件

铸造充型模拟的边界为固定边界，对于固定边界条件的施加，一般有三种方法：边界排斥力法、镜像虚粒子法和耦合边界法。针对充型模型中所用到的铸模几何形状复杂，采用边界排斥力法来处理固定边界。

Monaghan(1994)[12]在固定边界上布置一组虚粒子用于对邻近边界的实粒子产生排斥力，从而阻止邻近边界的这些实粒子非物理穿透边界。排斥力的表达式与计算分子力所使用的Lennard-Jones方程相似，即当边界虚粒子位于邻近边界的实粒子的影响域内，则会在沿着两粒子的中心线处对实粒子产生一个作用力：

(15)

其中，参数n1和n2满足n1>n2，且取值一般分别为12和4；系数D的取值一般由具体问题而定，一般取与速度最大值的平方相等的量级；截止半径r0的取值一般等于粒子的初始间距。

2　铸造充型模拟

本节所选取的两个算例来自Schmid和Klein(1995)[15]的铸造充型水模拟实验，铸模都由透明材料制成，并用高速摄像机记录充型过程。利用SPH方法来模拟这两个算例，均视为二维问题，时间积分采用跳蛙法，算例中流体都为水，密度为998kg·m-3，动力粘度为1.003×10-3Pa·s。

2.1弓型件充型

铸模几何尺寸如图1所示，整体上来看该型腔为“弓”字型，含有5个直角转角，2个弧形转角，底部入口处有一垂直延伸段以便水能够被腔壁约束顺利入腔。实验中水从型腔底部入口以8.7m·s-1的速度充入腔内，不计重力的影响。

SPH模拟中，在弓型件边界上布置4 290个虚粒子，水粒子有27 000个，粒子的初始间距为1mm，时间步长为2×10-7s；充型过程中粒子的最大速度大致为42m·s-1，则声速取420m·s-1，边界排斥力表达式(15)中D取值为1 764，截止半径r0=1mm。

本文SPH模拟文献[9]中模拟结果和实验结果如图2所示，共选取4个时间节点的结果进行比较，分别是7.15ms，25.03ms，39.34ms和53.64ms。

图1　弓型腔几何尺寸示意图

图2　图(a)～(d)为弓形件充型模拟的实验结果[15]、图(e)～(h)为文献[9]中模拟结果、图(i)～(l)为本文SPH仿真结果

在t=7.15ms时刻，水流通过第1个弧形转角，流向由垂直变为水平。两种SPH模拟结果基本都和实验保持一致，水头的位置和形态较相符。

在t=25.03ms时刻，水流到达第4个直角转角，并在第2个转角处形成空腔。从水的流态来看，两种模拟结果都与实验吻合得较好，比较精确地预测到水流在经过第4个转角后的水头所呈现出来的形态，但对于第2个转角处的空腔的大小的预测，都比实验值略小；另外本文结果中水头前端上升的高度比文献中要大，更符合实验结果。

在t=39.34ms时刻，水流经过第6个转角， 两种SPH模拟准确预测了水头撞击腔壁后所形成的水花的形状。对第3个转角到第4个转角之间的空腔的大小和形状的预测，本文结果与实验结果更相符；在第4个转角到第6个转角之间的空腔的预测上，文献中结果更客观；但两种SPH模拟结果中第2个转角处空腔都已经消失，可能的原因是SPH模拟中没有考虑气流的影响。

在t=53.64ms时刻，水流到达型腔顶部左边的腔壁，两种SPH模拟客观地捕捉第4个转角与第6个转角之间的空腔的位置；但第7个转角到顶部左边的腔壁之间的空腔，文献中SPH模拟与实验结果更相符。

2.2环型件充型

本算例模型是一个圆盘型中孔零件，实验中着色水以18m·s-1的速度从底部入口进入型腔，铸模几何尺寸如图3所示。

图3　环形腔几何尺寸示意图

SPH模拟中，在环型件边界上布置1 550个虚粒子，水粒子有30 910个，边界虚粒子的初始间距为0.4mm，水粒子的初始间距为0.8mm，时间步长为2×10-7s；充型过程中粒子的最大速度大致为40m·s-1，则声速取400m·s-1，边界排斥力表达式中D取值为1 600，截止半径r0=0.4mm。

图4给出了不同时刻实验和两种SPH仿真结果，其中SPH结果中还包含粒子轴向速度云图信息。

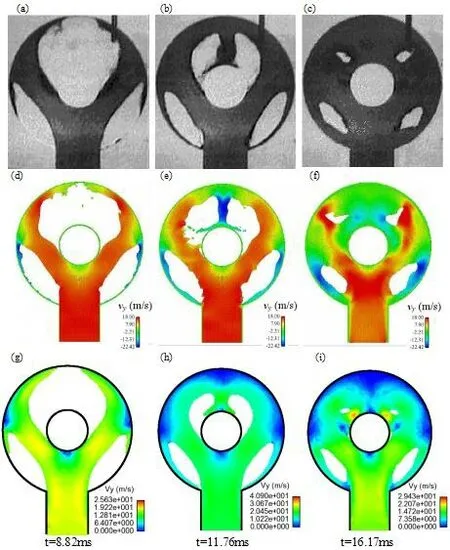
图4　图(a)～(c)为环形件充型模拟的实验结果[15]、图(d)～(f)为文献[9]中模拟结果、图(g)～(i)为本文SPH仿真结果

在t=8.82ms，水流通过下方垂直流道进入型腔冲击中心型芯，被分为两股支流，分别向型芯两侧流动继续充填型腔，在冲击型腔外轮廓后又再次分叉，分别沿壁面流向型腔顶部和底部，形成四股支流。两种SPH模拟与实验结果吻合程度都较高，水流形态和流向预测准确；但本文模拟结果中的流体粒子更有序。

在t=11.76ms，型腔顶部的两股支流汇合，冲向中心型芯上部，而底部的支流则继续沿型腔外轮廓流动，并与垂直流道进入型腔的水流汇合，形成左右两个空腔。两种SPH模拟对于水流走向和空腔形成预测基本准确，但对于型腔底部汇流后的水流冲向型芯上部后的形态的预测，本文模拟结果与实验更符合。

在t=16.17ms，型腔内出现 4个空腔，随着后续水流不断冲入型腔，空腔逐渐缩小并完成充型过程。本文SPH模拟捕捉到空腔的形成过程，且空腔形状饱满，粒子分布有序；但在本文模拟结果中上部两个空腔的大小比实验值略小，可能与气压有关。

从弓形件和环形件的充型模拟结果来看，本文SPH模拟结果比较客观地反映了水模拟充型实验进程，与文献[9]中的结果对比也说明了本文所采用对称结构的SPH离散公式，能够较成功地处理粒子不一致问题。

本文将光滑粒子流体动力学(SPH)方法应用到铸造充型问题上，通过构建弱可压缩流体的计算模型，利用SPH算法仿真水模拟铸造充型过程，并与文献中的模拟和实验结果比较，发现本文SPH算法结果不仅能够较准确地模拟流体自由表面的形态，而且对于流体走向和空腔的形成过程预测也比较吻合。在SPH算法设计中，控制方程采用具有对称结构的离散形式，动量方程压力项中加入人工粘度，利用边界排斥力法施加固定边界条件，这些技术的应用对于逼真的模拟效果起到显著作用。结果表明，本文所采用SPH方法及其技术处理对于模拟铸造充型过程是有效的。

[1]帕坦卡SV. 传热与流体流动的数值计算[M]. 郭宽良，译. 合肥：安徽科学技术出版社，1984：132-142.

[2]IssaRI.Solutionoftheimplicitlydiscretizedfluidflowequationbyoperatorsplitting[J].JournalofComputationalPhysics,1986,62：40-65．

[3]HarlowFH,WelchJE.Numericalstudyoflarge-amplitudefree-surfacemotions[J].PhysicsofFluid, 1966,9：842-851．

[4]HirtCW,NicholsBD.Volumeoffluid(VOF)methodforthedynamicsoffreeboundaries[J].JournalofComputationalPhysics,1981,39(1)：201-225．

[5]HarlowFH.PICanditsprogeny[C].WorkshoponParticleMethodsinFluidDynamicsandPlasmaPhysics.LosAlamos,NM,USA,13-15April1987．

[6]OsherS,FedkiwR.Levelsetmethods:Anoverviewandsomerecentresults[J].JournalofComputationalPhysics, 2001,169：463-502．

[7]LucyLB.Numericalapproachtotestingthefissionhypothesis[J].AstronomicalJournal，1977， 82：1013-1024.

[8]GingoldRA,MonaghanJJ.Smoothedparticlehydrodynamics:Theoryandapplicationtonon-sphericalstars[J].RoyalAstronomicalSociety，MonthlyNotices1977，181：375-389.

[9]曹文炅. 铸造充型过程SPH方法建模及数值模拟[D]. 广州：华南理工大学，2011年.

[10]强洪夫，韩亚伟，王坤鹏，等.基于罚函数SPH新方法的水模拟充型过程的数值分析[J].工程力学，2011，28(1)：245-250.

[11]LiuMB,LiuGR.SmoothedParticleHydrodynamics(SPH):anOverviewandRecentDevelopments[J].ArchComputMethodsEng， 2010，(17): 25-76.

[12]MonaghanJJ.SimulationfreesurfaceflowswithSPH[J].JournalofComputationalPhysics, 1994, 110: 399-406.

[13]MonaghanJJ.AnintroductiontoSPH[J].ComputerPhysicsCommunications, 1988, 48: 89-96.

[14]LattanzioJC,MonaghanJJ,PongracicH, et al.Controllingpenetration[J].SIAMJournalonScientificandStatisticalComputing, 1986, 7(2): 591-598.

[15]SchmidM,KleinF.Fluidflowindiecavities-experimentalandnumericalsimulation[C].Indianapolis:NADCA18.InternationalDieCastingCongressandExposition, 1995: 93-99.

责任编辑王菊平

A numerical study on foundry filling process based on SPH method

ZHOU Xue-jun1,2, CHEN Ding2

(1.College of Mathematics and Physics, Huanggang Normal University, Huangzhou 438000, Hubei, China;2. College of Mechanics and Materials, Hohai University, Nanjing 210098, Jiangsu, China)

Numerical simulation for foundry filling process is always a hot research topic of casting. Smoothed Particle Hydrodynamics (SPH) is presented to simulate foundry filling process in this paper. A mature meshless particle numerical method, the SPH method is good for mimicking large deformation. By establishing the model of filling process, the SPH method is applied to simulate water filling process of bow-shaped and annular models. Compared with the results of the literature and experiments, the SPH algorithm presented in this paper shows its advantages in solving foundry filling problems.

smoothed particle hydrodynamics; foundry filling; meshless; numerical simulation

TG21

A

1003-8078(2016)03-0012-06

2016-04-25

10.3969/j.issn.1003-8078.2016.03.04

周学君，男，湖北蕲春人，讲师，博士，主要研究方向为力学中的数值方法等。

湖北省教育厅科学技术研究项目(B2015218)。