关于多元凸函数性质的探讨

胡　芳

(武汉商贸职业学院 电商管理学院，湖北 武汉 430205)



关于多元凸函数性质的探讨

胡芳

(武汉商贸职业学院 电商管理学院，湖北 武汉 430205)

凸性及广义凸性问题已经引起了数学工作者们极大的兴趣与关注，并取得了很多重要结果，但是由于许多理论问题尚处于发展之中，很多结论仍有待进一步完善，对凸性的认识还需进一步系统化。文章充分运用文献研究法，在翻阅大量国内外的参考文献的基础上，给出线性拓扑空间中函数的凸性定义及等价定义，进一步完善多元凸函数的性质及判定等问题，从而丰富了凸函数的理论。

凸集；多元凸函数；凸性

近2个世纪，凸函数的研究主要有以下几个方面： 其一，凸函数的应用研究.Jensen首次给出凸函数的概念. 自建立凸函数理论以来，许多数学工作者都致力于一元凸函数在不等式中的应用，如Jensen、Holder不等式的巧妙应用[1]，使证明简练明了.其二，凸函数的性质研究.徐海岩介绍二元函数诸如有界性、连续性等性质[2]，f(x)凸性与f(x)的上图凸性关系[3]，凸之和仍凸、复合函数的凸性,由f(x)的凸性推及到g(x)=(f(x)+|f(x)|)f(x)的凸性，并给出了此性质在求解线性与非线性不等式组及线性规划中的应用[4].其三凸函数的判定研究.杨新民在文献[5]研究了拟凸函数构成凸函数的条件，连续凸函数的判定定理[6].

凸性及广义凸性问题已经有很多重要的结果.但仍然有许多理论问题尚处于发展之中，有待进一步完善和系统化，笔者力求通过本文的研究，给出凸函数较为全面、系统地介绍.

定义1设D⊂Rn是非空开集，若对∀x,y∈D，及任意实数λ∈[0,1]，恒有：λx+(1-λ)y∈D，则称D是凸开集[5]．

定义2设D⊂Rn是凸开集，f是定义在D上的n元实值函数[5]，若对∀x,y∈D，及∀实数λ∈[0,1]，恒有：

(1)

则称f是D上的下凸函数，简称凸函数．

注：-f是D上的下凸函数，则称f是D上的凹函数．

若当λ∈[0,1]且x≠y时,(1.1)中的不等式为严格不等式，则称f是D上的严格凸函数．

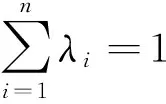
则称f是D上的凸函数．

定义4设D⊂Rn是凸开集，若f是定义在D上的n元实值函数，称图像空间Rn+1=Rn×R中的集合epif为f的上图，其中epif={(x,c)T∈D×R|f(x)≤c}.

定义5设D⊂Rn是凸集，若f是定义在D上的n元实值函数，称集合S(f,c)为水平集,

定理1定义2与定义3等价．

证明定义3⟹定义2显然．

用数学归纳法证明定义2⟹定义3

n=2，显然成立.

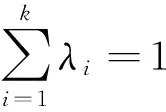
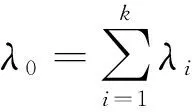
(2)

由归纳假设知，

(3)

定理2设D⊂Rn是凸开集，f是定义在D上的n元函数，则f是凸函数的充要条件是epif是Rn+1中的凸集.

证明先证“⟹”.

f∶D→R是凸函数.设任意(x,c1)T、(y,c2)T∈epif，即：f(x)≤c1，f(y)≤c2

由f凸性知：f[λx+(1-λ)y]≤λf(x)+(1-λ)f(y)≤λc1+(1-λ)c2

则有：(λx+(1-λ)y,λc1+(1-λ)c2)T∈epif

λ(x,c1)T+(1-λ)(y,c2)T∈epif

可知：epif是Rn+1中的凸集.

再证“⟸”.设epif是Rn+1中的凸集. ∀x,y∈D，∀λ∈[0,1]

若(x,f(x))T∈epif，(y,f(y))T∈epif，由epif的凸性得：

从而f是凸函数.

定理3设D⊂Rn是凸开集，f、g分别都是定义在D上的n元实值凸函数，则h(x)=max{f(x),g(x)}也是D上的凸函数[7].

定理4设D⊂Rn是凸开集，f、g分别都是定义在D上的n元实值凸函数，则Φ(x)=μ1f(x)+μ2g(x)也是D上的凸函数[7]，其中常数μ1≥0， μ2≥0.

定理6设D⊂Rn是凸开集,f是定义在D上的n元实值函数，∀x,y∈D，令F(∂)=f(∂x+(1-∂)y),∂∈[0,1]，则f是D上的凸函数的充要条件是F(∂)在[0,1]上是凸的[8].

定理7设D⊂Rn是凸开集, f是定义在D上的n元实值非负凸函数，若S(x)=f2(x),则S(x)也是D上的凸函数.

证明由f是非负凸函数，∀x,y∈D，∀λ∈[0,1]，有：

即：

(4)

又

则：

(5)

结合式(4)、(5)得：

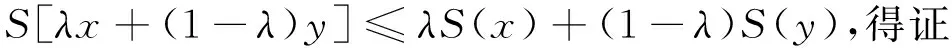
推广定理7可得：

定理8设D⊂Rn是凸开集, f和g都是定义在D上的n元实值凸函数，且f和g是具有相同单调性的单调函数，又f(x)≥0，g(x)≥0，若W(x)=f(x)g(x),则W(x)也是D上的凸函数.

证明 由f和g都是凸函数，∀x,y∈D，∀λ∈[0,1]，有：

(6)

又

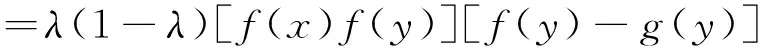
若f(x)=f(y)≡C或g(x)=g(y)≡C，其中C为常数.由定理4，结论显然.

若f和g不恒为常函数，又f和g是具有相同单调性的单调函数，则有：

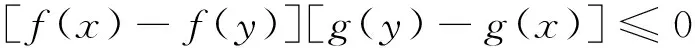
则有：

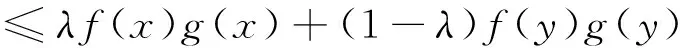
(7)

由式(6)、(7)得：

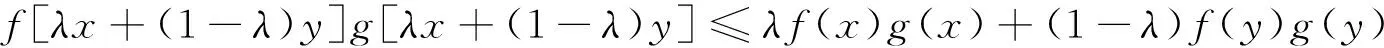
即W(x)是D上的凸函数.

证明仅就限制在Dxi上的情况进行证明.

则有：

即：f[λx+(1-λ)y]≤λF(x)+(1-λ)F(y).

注：当沿某一方向上f(p)是凸函数，并不足以说明f是D上的凸函数.

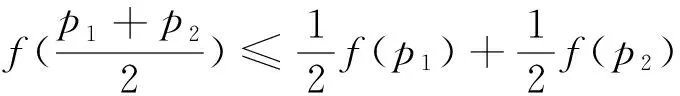
定理10设D⊂Rn是凸开集, f是定义在D上的n元实值凸函数，f(x)是凸函数的充要条件是f限制在任何的Dxi上是一元凸函数，

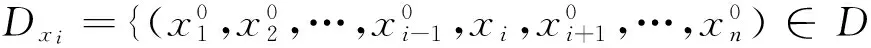
证明“⟹”定理9已证.

下证“⟸”，f限制在任何的Dxi上f(x)是一元凸函数，设∀s,t∈D，(s≠t)

定义F(u)=f(x0+au)且由充分性假设F(u)是一元凸函数得：

从而有： f[λs+(1-λ)t]≤λf(s)+(1-λ)f(t)，即f(x)是凸函数.

[1]徐娜.凸函数的性质及应用[J].数学学习与研究,2013,(13):117.

[2]徐海岩.多元凸函数的某些性质[J].湖北师范学院学报(自然科学版)，1988,7(1): 90-94.

[3]蒋善利,普丰山.凸函数的性质与判断[J].新乡学院学报(自然科学版),2009,26(6):13-14.

[4]时贞军.r-凸函数与几个重要不等式的联系与应用[J]. 四川师范大学学报(自然科学版),2010,33(5):703-706.

[5]Yang X M, Teo K L, Yang X Q. A Characterization of Convex Function[J].Applied Mathematics Letters,2000,13(1):27-30.

[6]陶有德,朱叶,陶亦文.连续凸函数的判定定理[J].淮北师范大学学报(自然科学版),2012,33(3): 27-29.

[7]Rockafellar R T.Convex Analysis[M].Pinceton University Press,1970.

[8]陈乔.E-凸函数的一个新性质[J].重庆师范大学学报(自然科学版),2008,25(4):8-11.

责任编辑王菊平

A discussion about the properties of the multivariate convex function

HU Fang

(School of E-Business Management, Wuhan International Trade College, Wuhan 430205, Hubei, China)

Convexity and generalized convexity problems have aroused great interest in and attracted great attention of professionals of mathematics, and many significant achievements have been attained. However, because of the underdevelopment of many theories, many conclusions remain imperfect and the understanding of convexity needs to be further systematized. Applying literature research method and based on numerous domestic and international literature, the paper presents convexity definition and equivalence definition of linear space of convex function in linear topological space. By doing so, it is supposed to further improve the properties and determination of multivariate convex function, so as to enrich the theory of convex function.

convex set; multiple convex function; convexity

O1

A

1003-8078(2016)03-0004-04

2016-03-17

10.3969/j.issn.1003-8078.2016.03.02

胡芳，女，湖北武汉人，讲师，主要研究方向为基础数学。