引入大颗粒助剂对径向移动床流动特性的影响

卫思辰，贾海兵，范怡平，卢春喜

（中国石油大学（北京）重质油国家重点实验室，北京 102249）

引入大颗粒助剂对径向移动床流动特性的影响

卫思辰，贾海兵，范怡平，卢春喜

（中国石油大学（北京）重质油国家重点实验室，北京 102249）

针对错流移动床存在的空腔和颗粒流动偏离平推流的不正常操作问题。在一套φ600 mm×1300 mm半圆锥形和柱形错流移动床大型冷模实验装置上，借助于大颗粒助剂的引入有效提高了错流移动床出现空腔的临界速度，解决了错流移动床操作弹性低的问题。理论分析和实验结果表明，混入适量的大颗粒助剂可使颗粒流动不均匀性得到明显改善。

移动床；空腔；颗粒物料；流动；

引　言

移动床反应器是一种颗粒速度介于固定床反应器和流化床反应器之间的多相反应器。按流固运动方向可将移动床分为并流式、逆流式和错流式 3种。错流式移动床具有气体压降低、流固两相接触均匀以及固体停留时间调节弹性大等优点，广泛应用于催化重整、颗粒干燥、过滤等领域［1-5］。

在操作过程中，移动床内颗粒受到径向错流气体的作用，当气速较高时（达到“临界气速”），将使靠近气体进口壁面（上流面）的颗粒与壁面相脱离，在上流面与颗粒床层之间形成空腔（cavity）［6］。多年来，研究者们对于空腔的研究大多集中于空腔发生的初始条件以及空腔的增长理论［7-12］。对于如何抑制空腔，陈允华等［13］、曹晏等［14］发现床层设置内构件可改变空腔的临界气速。此外，陈允华等［15］通过实验和模拟认为采用密度大、粒径大、壁摩擦角小的颗粒可以减小空腔尺寸。许鹏凯等［16］采用离散元方法研究得出在移动床中混入粗颗粒能够抑制空腔的形成，但并未有相关实验数据予以验证。

通常在操作中要求移动床反应器内颗粒运动为平推流，从而实现气固两相均匀接触，颗粒停留时间分布均一［17］。但是颗粒与器壁之间的摩擦力以及气体对颗粒的曳力都会影响颗粒的均匀运动，径向风会造成反应器内的颗粒运动由稳定的平推流转变为漏斗流［18］。武锦涛等［19］采用微观尺度DEM模型分析了颗粒粒径分布和移动床出口直径对颗粒运动的影响，认为粒径分布对颗粒垂直速度分布有很大影响，不同粒径的混合有利于颗粒的流动。

由此可见，以往对于移动床中混入大颗粒助剂的考察大多属于模拟分析，未有实验验证。本文通过大型冷模实验，在锥形移动床与柱形移动床中混入不同比例粒径较大的助剂颗粒，考察大颗粒混入比例对空腔这一非正常操作工况的影响。采用光纤颗粒测速仪测量排料区的局部颗粒速度分布，分析大颗粒的混入是否可以抑制由于径向气流引起的颗粒速度的不均匀分布。

1　实验装置与测试方法

1.1实验装置与介质

图1　径向移动床装置Fig.1　Schematic diagram of experimental setup

实验装置如图1所示。主要由罗茨风机、缓冲罐、转子流量计、提升管、移动床、下料段、分离罐等构成。实验装置主体由φ 600 mm×1300 mm半圆锥形和柱形错流移动床构成，装置总高为 5000 mm，移动床内的中心管和扇形筒选用催化重整工业装置使用的约翰逊网，约翰逊网高度1100 mm、缝隙 0.4 mm、开孔率 23.5%。提升管由φ 60 mm×3400 mm的有机玻璃构成。分离罐由φ 200 mm×1000 mm的有机玻璃构成，在分离罐顶部加装了0.5 mm孔径的钢丝筛网。柱形床横截面内环半径为0.054 m，外环半径为0.246 m；锥形床横截面内环半径为0.054 m，顶部外环半径为0.159 m，底部外环半径为0.246 m。

空气由罗茨风机进入缓冲罐，经转子流量计分别进入提升管与径向移动床，提升管内气体垂直输送颗粒后进入分离罐，移动床内气体沿径向穿过床层后与离开分离罐的气体汇集进入布袋除尘器，除尘后的空气排入大气。移动床内的固体颗粒依靠重力向下流动，然后经过下料段，最后通过底部斜管进入提升管，在气体提升作用下垂直向上运动进入分离罐，在分离罐内依靠气固两相密度差实现分离，固体颗粒通过顶部斜管返回移动床形成颗粒的循环。

图2为径向移动床结构 ，在移动床主体区从上到下均匀布置8个径向进气通道来保证气体的均匀分布。空气通过上流面约翰逊网的缝隙进入移动床，气体在移动床中沿水平方向流动与颗粒接触，最后通过下流面约翰逊网的孔隙离开移动床。气体的流量由截止阀控制，并由转子流量计计量。

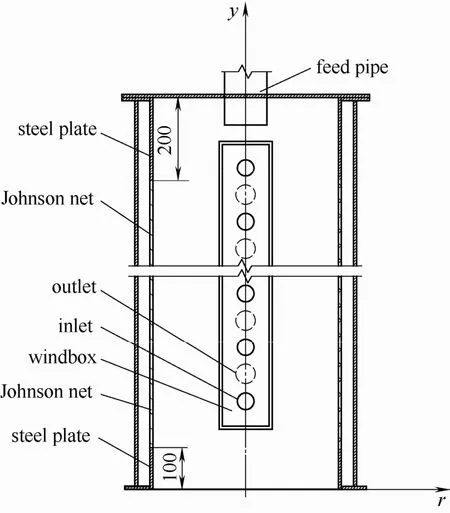
图2　径向移动床结构Fig.2　Moving bed structures

实验中，气体介质为常温空气，固体介质为两种不同粒径的催化剂担体，其物性参数见表 1。其中，“正常”颗粒是指工业用移动床所使用的颗粒，一般是1.65 mm左右的单一尺寸的颗粒，最大不会超过2 mm。本研究选择4 mm“大颗粒”是因为其与正常颗粒有足够的粒径差又不会过大从而影响移动床的正常运行。

表1　颗粒物性参数Table 1　M ain properties of particle

1.2实验方法

实验中，在锥形移动床与柱形移动床中混入 4 mm大颗粒，质量分数分别为3%、5%、10%、20%，并且与床层内全部为1.65 mm小颗粒时的工况进行对比。采用视频观察出现空腔的特征及其随时间的变化，记录径向移动床出现空腔时的临界条件。采用 PV-6M型移动床颗粒速度测量仪测量床层内部颗粒速度。

测量移动床排料区的局部颗粒速度分布时，在y=140 mm处沿横向分别布置6个测点，其量纲1横坐标与测点布置如图3所示。

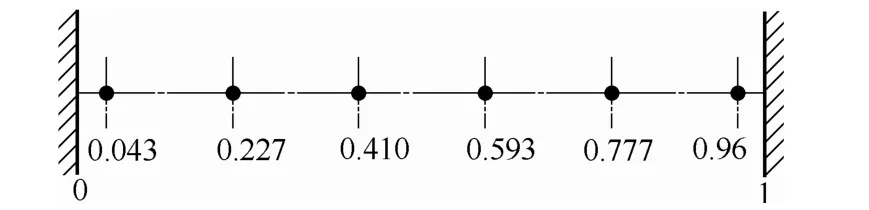
图3　颗粒速度分布测点Fig.3　Measurement points of particle velocity distribution

2　实验结果与讨论

2.1混入大颗粒助剂对空腔的影响

当没有气体通过床层时，床层内颗粒均匀向下流动，颗粒速度对称分布。当有少量气体通过床层时，床层内部所有颗粒继续向下运动，但颗粒速度分布开始变得不均匀，近上流面颗粒速度变大，近下流面颗粒速度变小，上流面附近颗粒速度边界层变薄，而下流面附近颗粒速度的边界层变厚。

继续增加气体流量，空腔开始形成。以锥形床为例，当径向气体流量Q=560 m3·h-1（ug=0.3 m·s-1）时，在上流面约翰逊网顶端形成了一个微小的空穴，空穴内没有颗粒相，如图4（a）所示。此时开始出现空腔，对应的表观气速即为空腔临界气速。空腔在床层内是动态的，经历“形成—变形—破碎”3个连续的过程。床层上流面左侧先出现空腔（此时上流面右侧并未出现空腔）。上流面左侧空腔呈半圆形，半径约为12 mm。圆形空腔维持16 s后，呈攀爬状消失，前后两次出现空腔间隔时间为110 s，且现象一致。气体流量达到 575 m3·h-1（ug=0.31 m·s-1）时，上流面左侧出现一个稍大的空腔，呈半椭圆形，且空腔内有明显颗粒流化现象，如图4（b）所示。同时，上流面的右侧也出现空腔，左侧空腔半径约为19 mm，右侧为13 mm。前后两次空腔的间隔时间缩短至58 s，且现象一致。

图4　锥形床空腔尺寸Fig.4　Schematic diagram of cavity size in semi-conical

继续增加表观气速，锥形床气体流量达到 610 m3·h-1（ug=0.33 m·s-1），进料管中的颗粒不能进入床层，而床层中的颗粒继续向下运动，床层出现一个较大的空腔，出现了气阻现象，移动床不能正常操作，如图5所示。此时的表观气速为气阻临界气速［18］。

在锥形床和柱形床中按不同质量分数混入 4 mm颗粒，实验测得的空腔临界气速与气阻临界气速如图6所示。实验发现，随着大颗粒助剂混入比例的增大，移动床空腔临界气速增大，而气阻临界气速大幅度下降。

柱形床中，混入大颗粒比例为 3%时空腔临界气速提高不明显；当混入比例为 5%时提升较为明显，并且在操作范围内（Q=1000 m3·h-1），装置未出现气阻现象；混合比例提至10%时空腔临界气速依旧在增大，并且随着径向气流的增大装置开始出现气阻现象；然而当混入比例为20%时，由于装置气阻临界气速明显降低，装置先出现气阻现象，停止运转。

图5　气阻现象Fig.5　Schematic diagram of air lock

图6　临界气速与大颗粒助剂质量分数的关系Fig.6　Relationship of critical gas velocity w ith mass fraction of large particle

在锥形床中，其本身的操作弹性较柱形床高［20］，所以其空腔临界气速较柱形床高。与柱形床相似，在混入比例超过10%时，床层中还未出现空腔，但由于气阻的形成装置已不能运转。

空腔临界气速随着大颗粒助剂的混入而提高，这是因为随着颗粒粒径的增大，颗粒所受到的曳力以及颗粒本身的重力都变大，但是两者的比值减小［21］。所以，在同一径向气速下，气体对颗粒的曳力对支撑大颗粒的贡献弱于对支撑小颗粒的贡献。因此，当床层中混入大颗粒后，曳力对于支撑颗粒群的贡献也被削弱，进而有利于增大形成空腔的临界气速。按照理论来说，混入大颗粒越多，床层的空腔临界气速也会越大，这与实验观察到的一致。

2.2混入大颗粒助剂对颗粒流动均匀性的影响

理想的移动床反应器内颗粒运动为平推流，有利于实现气固两相均匀接触。但是颗粒与器壁之间的摩擦力以及气体对颗粒的曳力都会影响到颗粒速度的均匀分布。

以柱形床为例，本文首先在未混入任何大颗粒助剂时通过光纤颗粒测速仪分别在径向气体流量Q为0、229 （ug=0.12 m·s-1）、275 m3·h-1（ug=0.15 m·s-1）时测量y=140 mm处的局部颗粒速度，如图7所示。

图7　未混入大颗粒时颗粒速度的横向分布Fig.7　Horizontal distribution of particles velocity before introducing large particle

加入径向气流以后边壁处的颗粒速度有明显下降，同时中间的颗粒速度会相应地增加。这是因为在径向气流的作用下边壁与颗粒的摩擦增大，因此降低了边壁附近的颗粒流速。因为移动床中的径向气流对颗粒的流动状态有影响，径向气速的增大会造成颗粒流动由平推流向漏斗流发展，气体径向速度越大，颗粒的速度分布越不均匀。

为了描述颗粒运动的不均匀性，本文采用Zhu等［22］提出的径向不均匀指数RNI来定量地表示局部颗粒速度的径向分布不均匀性。在实验操作条件范围内，移动床床层空隙率基本不变，因此局部颗粒速度Vp的径向不均匀指数为

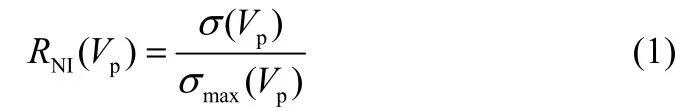
式中，σ（Vp）为局部颗粒速度沿截面的标准偏差，σmax（Vp）为给定截面平均颗粒速度的最大可能标准偏差。

σmax（Vp）为归一化参数，RNI（Vp）在0～1变化，其值越大表示颗粒速度径向分布越不均匀。Vp，m in为可能的最小局部颗粒速度，取值

图8　混入大颗粒后颗粒速度的横向分布Fig.8　Horizontal distribution of particles velocity after introducing large particles

Vp，max为可能的最大局部颗粒速度，由局部颗粒速度实验数据确定。

把式（2）～式（4）与实验获得的局部颗粒速度最大值代入式（1）即可得到颗粒速度径向不均匀指数。

由计算得知，在没有通入径向气流（ug=0）时，径向不均匀指数为0.0230，趋近于0，所以此时颗粒流动很均匀接近于平推流；而当通入径向气流后，表观气速ug为0.12 m·s-1和0.15 m·s-1时不均匀指数分别为0.0992与0.1219，说明径向气流会对颗粒的流动状态有影响，气体径向速度越大，颗粒的速度分布越不均匀。

为了观测混入大颗粒助剂对于这种不利发展是否有减缓作用，本文在混入不同比例大颗粒时测量相同测点的局部速度，如图8所示。

图9　不均匀指数Fig.9　Radial non-uniformity index

利用上述公式分别计算径向不均匀指数，如图9所示。由图可以明显看出混入大颗粒助剂可以减缓由于径向气速的增加而导致的颗粒流动向漏斗流的发展，但无法完全使排料区的颗粒呈平推流运动。

由于颗粒流动的不均匀分布是由径向风引起的，现假设床层中存在一个单位面积的微元，对其进行受力分析如图10所示。

已知曳力为

混入大颗粒后孔隙率增大，这一微元中径向风与颗粒接触面积减小，所以对其内颗粒群来说所受到的曳力会随着大颗粒的混入而变小。颗粒群所受到的平行于径向风方向的分力减小，合力使得颗粒更容易向下流动，进而床层中颗粒流动变均匀。

图10　受力分析Fig.10　Force analysis

由图8、图9得知，当混入比例为3%时，大颗粒助剂对颗粒流动的影响仍不明显；比例达到10%时颗粒流动随着径向气速的增大而导致的漏斗流得到有效控制，与改善空腔问题时一样，此时为最佳混入比例。

当混入比例为20%时，装置运行开始变得不稳定，按照理论分析，混入比例越大，颗粒群所受曳力越小，颗粒流动应该越稳定。但是在实际操作过程中，装置运行存在一个拐点，混入比例为20%时，由于下料口直径较小，并且含有较大比例的大粒径颗粒，在向下输送催化剂时，管内催化剂正常流动被破坏，出现了催化剂梗塞、气节等现象，梗塞处虽有催化剂慢速塌落或有少量催化剂流动，但催化剂的流率小于正常时的流率，梗塞处上部的催化剂堆积密度不断增大而下部无料，此时不能自行疏通，产生轻微架桥现象从而导致装置运行不稳定，影响颗粒流动的均匀性。

武锦涛等［19］认为颗粒的粒径分布对颗粒垂直速度分布有很大影响，不同粒径的混合有利于颗粒的流动。比较图8中在不同比例大颗粒的床层中未通入径向风（ug=0 m·s-1）时平均速度如图11所示。由图可知，混入大颗粒使得颗粒流速增大，然而当混入比例过大时，产生的架桥现象使得颗粒流速下降、颗粒流动不均匀，与实验结果相吻合。

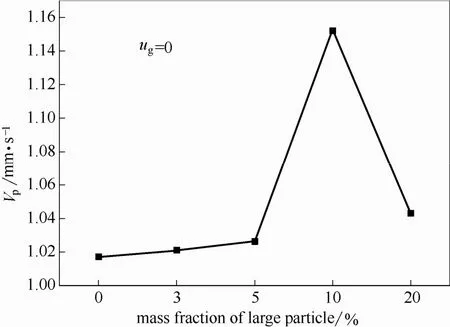
图11　颗粒流速与大颗粒助剂质量分数的关系Fig.11　Relationship of average velocity w ith mass fraction of large particle

2.3颗粒运动模型

本文采用Nedderman等［23］提出的“运动模型”来描述颗粒的流动。假定颗粒的运动完全是由重力引起的，颗粒流动产生的空隙马上会被临近的颗粒所补充。如图12所示，考察3个相邻的颗粒，其中颗粒2和颗粒3在一层，且在颗粒1的下一层。颗粒2和颗粒3具有不同的速度分布，很明显当颗粒2的速度更快时，颗粒1有向颗粒2运动的趋势。由此可以假定颗粒水平运动的速度ur是垂直运动速度vy梯度的函数，即

图12　颗粒运动的随机模型Fig.12　Stochastic model of particle flow

并且ur与之间仅存在线性关系，引入一个动力学参量B，则

由于颗粒流动为不可压缩流动，连续性方程为

将式（7）代入式（8）中可得

式（9）中B由实验测定。Nedderman等［23］指出B只与颗粒的大小有关，一般为颗粒直径dp的2～3倍。

由式（7）与式（9）可以推知，随着平均粒径的增大，垂直运动速度梯度与水平运动速度梯度变化趋势如表2所示。

表2　速度随粒径变化趋势Table 2　Variety of velocity w ith particle size

由表2可得，随着粒径的增大，颗粒垂直速度增大，并且颗粒水平运动速度梯度减小，即运动的速度增大以及流动不均匀性减缓，与实验结果相符。

3　结　论

通过在错流移动床中混入大颗粒助剂显著改善了移动床操作中存在的空腔和颗粒流动不均匀的问题。结合实验结果以及理论分析得出结论如下。

（1）混入大颗粒助剂可显著提高移动床的操作弹性，空腔的临界气速随着混合比例的增大而提高，但是混合比例过大时会造成气阻临界气速的大幅度降低。

（2）径向错流气体会对移动床的颗粒运动产生影响，使得颗粒流动由平推流向漏斗流转变，混入大颗粒助剂会使得颗粒群受到的曳力减小，从而“减缓”这种转变，但并不能完全消除漏斗流。

（3）在本文实验条件下，从最大限度提高空腔临界气速和保持颗粒均匀流动的综合分析，混入大颗粒的比例在5%～10%最为理想。

符号说明

A ——迎风面积（流动方向颗粒的投影面积），m2

CD——曳力系数

dp——颗粒直径，mm

F ——合力，N

FD——曳力，N

G ——重力，N

Gs——颗粒循环强度，kg·m-2·s-1

Q ——径向气体流量，m3·h-1

RNI——径向不均匀指数

r——横坐标，mm

ug——径向气体流速，m·s-1

ur——颗粒水平运动速度，m·s-1

ut——流体与颗粒间的相对运动速度，m·s-1

Vp——局部颗粒速度，m·s-1

vy——颗粒垂直运动速度，m·s-1

y——纵坐标，mm

ρ——流体密度，kg·m-3

ρb——颗粒堆积密度，kg·m-3

σ——标准偏差

φ ——直径，mm

References

［1］ EL-HEDOK I A， WHITMER L， BROWN R C. The influence of granular flow rate on the performance of a moving bed granular filter［J］. Powder Technology， 2011， 214（1）: 69-76.

［2］ 张世方. 催化重整工艺技术发展［J］. 中外能源， 2012， 17（6）: 60-65.

ZHANG S F. Catalytic reform ing process technology development［J］. Sino-global Energy， 2012， 17（6）: 60-65.

［3］ PAENPONG C， PATTIYA A. Filtration of fast pyrolysis char fines w ith a cross-flow moving-bed granular filter［J］. Powder Technology，2013， 245（8）: 233-240.

［4］ TALLMAN M J， ENG C. Naphtha cracking for light olefins production［J］. Petroleum Technology Quarterly， 2010， 15（4）: 87-91.

［5］ ZHAO J， HUANG J， WU J， et al. Modeling and optim ization of the moving granular bed for combined hot gas desulfurization and dust removal［J］. Powder Technology， 2008， 180（1）: 2-8.

［6］ BRIDGEWATER J. New territory: the chem ical processing of solids: inaugural lecture of University of Birm ingham［R］. London: Macm illan， 1981

［7］ III F J D， JACKSON R， GINESTRA J C. The phenomenon of pinning in an annular moving bed reactor w ith crossflow of gas［J］. Chem ical Engineering Science， 1986， 41（6）: 1485-1495.

［8］ TAKAHASHI H， OHNO O， TAKEUCHI T. Analysis of gas flow in a solid-gas cross flow moving bed by the finite element method.［J］. Kagaku Kōgaku Ronbunshū， 1990， 16（1）: 116-122.

［9］ 王保平， 庞桂赐， 金涌. 径向移动床反应器内贴壁现象的研究［J］.石油学报（石油加工）， 1993， 9（3）: 78-87.

WANG B P， PANG G C， JIN Y. Study of pinning in a radial moving bed reactor［J］. Acta Petrol. Sin. （Petrol. Process Section），1993，9（3）:78-87.

［10］ PILCHER K A， BRIDGWATER J. Pinning in a rectangular moving bed reactor w ith gas cross-flow［J］. Chem ical Engineering Science，1990， 45（8）: 2535-2542.

［11］ 宋续祺， 金涌， 俞芷青， 等. 移动床径向反应器中气体离心流动对颗粒移动状况的影响［J］. 化工学报， 1993， 44（4）: 433-441.

SONG X Q， JIN Y， YU Z Q， et al. The formation of cavity in moving bed radial flow reactor［J］. Journal of Chem ical Industry and Engineering（China）， 1993， 44（4）: 433-441.

［12］ RAJNEESH S， GUPTA G S. Importance of frictional forces on the formation of cavity in a packed bed under cross flow of gas［J］. Powder Technology， 2003， 134（134）: 72-85.

［13］ 陈允华， 朱学栋， 吴勇强， 等. 整流子对错流移动床颗粒行为的影响［J］. 过程工程学报， 2007， 7（4）: 639-645.

CHEN Y H， ZHU X D， WU Y Q， et al. Effects of internals on the particle behavior in a rectangular moving bed with gas cross-flow［J］. The Chinese Journal of Process Engineering， 2007， 7（4）: 639-645.

［14］ 曹晏， 张建民， 王洋， 等. 内构件对矩形移动床床内颗粒流动影响的试验研究［J］. 化学工业与工程， 1999， 16（2）: 3-7.

CAO Y， ZHANG J M， WANG Y， et al. The experimental study on the effects of internals on particle flow in rectangular moving bed［J］. Chemical Industry and Engineering， 1999， 16（2）: 3-7.

［15］ 陈允华， 朱学栋， 吴勇强， 等. 移动床空腔现象及空腔尺寸［J］. 化工学报， 2006， 57（4）: 731-737.

CHEN Y H， ZHU X D， WU Y Q， et al. Phenomenon of cavity and its size in rectangular moving bed［J］. Journal of Chemical Industry and Engineering（China）， 2006， 57（4）: 731-737.

［16］ 许鹏凯， 段学志， 钱刚， 等. 混入粗颗粒对移动床中空腔的抑制效应［J］. 化学反应工程与工艺， 2015， 31（4）: 289-296.

XU P K， DUAN X Z， QIAN G， et al. Inhibiting cavity formation by mixing coarse particles into a moving bed［J］. Chemical Reaction Engineering and Technology， 2015， 31（4）: 289-296.

［17］ 曹晏， 张建民， 王洋， 等. 渐缩下料段对其上柱形移动床内床层颗粒流动的影响［J］. 化学工业与工程， 1997， 14 （4）: 5-10.

CAO Y， ZHANG J M， WANG Y， et al. The effects of hoppers on particle flow in rectangular moving bed［J］. Chemical Industry and Engineering， 1997. 14 （4）: 5-10.

［18］ 龙文宇. 气固错流移动床流动特性［D］. 北京:中国石油大学（北京），2014.

LONG W Y. Hydrodynamic characteristics of cross-flow moving beds［D］. Beijing：China University of Petroleum， 2014.

［19］ 武锦涛， 陈纪忠， 阳永荣. 移动床中颗粒运动的微观分析［J］. 浙江大学学报（工学版）， 2006， 40（5）: 864-868.

WU J T， CHEN J Z， YANG Y Y. M icroscopic analysis of particle flow in moving bed［J］. Journal of Zhejiang University（Engineering Science）， 2006， 40（5）: 864-868.

［20］ 龙文宇， 徐军， 范怡平， 等. 梯形移动床径向反应器内颗粒的贴壁现象分析［J］. 化工学报， 2014， 65（4）: 1179-1185.

LONG W Y， XU J， FAN Y P， et al. Phenomenon of pinning in trapezoidal moving beds w ith cross-flow［J］. CIESC Journal， 2014，65（4）: 1179-1185.

［21］ WU C L， AYENI O， BERROUK A S， et al. Parallel algorithms for CFD-DEM modeling of dense particulate flows［J］. Chemical Engineering Science， 2014， 118（18）: 221-244.

［22］ ZHU J X， MANYELE S V. Radial nonuniformity index （RNI） in fluidized beds and other multiphase flow systems［J］. Canadian Journal of Chemical Engineering， 2001， 79（2）: 203-213.

［23］ NEDDERMAN R M， TÜZÜN U. A kinematic model for the flow of granular materials［J］. Powder Technology， 1979， 22（2）: 243-253.

Effect of introducing large additive particles on flow characteristics in radial flow moving bed

WEI Sichen， JIA Haibing， FAN Yiping， LU Chunxi
（State Key Laboratory of Heavy Oil， China University of Petroleum （Beijing）， Beijing 102249， China）

It does exist that some of abnormal phenomena， such as cavities and particle flow variations from plug flow， are inevitable in cross-flow moving bed operations. In terms of the issues related to the abnormal operation phenomena， the experiment was conducted through a large cold model experimental facility consisting of a φ600 mm×1300 mm semi-conical and sem i-cylindrical radial flow moving bed. It showed that， the critical velocity of form ing cavity can be effectively increased through introducing coarse additive particles， hence the low elasticity of operation can be improved in cross-flow moving bed to some extent. Both theoretical analysis and experimental results showed that， the inhomogeneity of particle flow can be effectively improved by introducing coarse additive particles.

moving bed；cavity；granular materials；flow

date: 2016-03-28.

FAN Yiping，fanyipin2002@yahoo.com

supported by the National Basic Research Program of China （2012CB215000）.

TQ 021.1

A

0438—1157（2016）08—3313—08

10.11949/j.issn.0438-1157.20160358

2016-03-28收到初稿，2016-05-12收到修改稿。

联系人：范怡平。第一作者：卫思辰（1992—），女，硕士研究生。

国家重点基础研究发展计划项目（2012CB215000）。