两自由度磁力悬浮非线性振动能量采集研究

王祖尧, 丁　虎， 陈立群, 3

(1.上海大学 上海市应用数学和力学研究所，上海　200072；2. 浙江科技学院 理学院，杭州　310023； 3. 上海大学 力学系，上海　200444)



两自由度磁力悬浮非线性振动能量采集研究

王祖尧1, 2, 丁虎1， 陈立群1, 3

(1.上海大学 上海市应用数学和力学研究所，上海200072；2. 浙江科技学院 理学院，杭州310023； 3. 上海大学 力学系，上海200444)

首次研究通过增加自由度数，扩大磁力悬浮非线性能量采集器的采集区域。通过引入线性弹簧振子，将单自由度非线性磁力悬浮能量采集器扩展到两个自由度。使用谐波平衡法近似分析两自由度非线性常微分方程组，研究位移激励下系统主共振的稳态幅频响应特征。研究结果表明，两自由度系统能够显著扩展系统的共振区域。还通过对比系统各个参数对共振幅频响应幅度以及区域的影响，研究了系统质量比、频率平方比和非线性系数比对增强共振强度、扩大共振区域，也就是提高能量采集的强度和带宽的影响。另外，还通过直接的数值模拟验证了近似解析分析结果的正确性。

非线性；振动；磁悬浮；能量采集；谐波平衡

现代科技中，无线电子设备在生物医学设备、计算机系统、便携式电子产品、以及导航系统等领域都有着广泛的应用。这些无线设备中多是使用电池作为其电源，而更换电池和处理废旧电池都需要额外增加使用费用。而另一个方面，随着超大规模集成电路设计的水平提高,无线电子设备的功耗从毫瓦数量级降低到微瓦数量级。因而，振动能量采集器为这种无线设备提供电源就成为可能。国内外许多研究人员已经对这种微机系统提供电源的振动能量采集进行研究[1-5]，力图提高振动能量的采集的效率和扩大采集的频率范围。JIANG等[6]研究了单稳态的能量采集器在高斯白噪音激励下的能量采集的强度。也有一些学者试图从多稳态的能量采集的角度增加能量采集的强度[7-9]。这些研究都发现，引入非线性因素能够增加能量采集的带宽。通过非线性磁力作用，ZHU等[10]提出了一种新型的磁悬浮能量采集器，实验表明这种设计可以增加能量的采集强度并扩展采集的频带宽度。MANN等[11]通过单自由度弹簧振子的非线性振动特性分析，对这种磁悬浮的装置的非线性能量采集性能进行了近似解析分析，得到了幅频响应关系，从理论上分析了这种非线性能量采集原理。

本文在文献[10-11]的能量采集装置中增加了一个线性弹簧振子，便于调节非线性振动能量采集的频率。进一步建立两自由度非线性振动方程组，通过谐波平衡方法研究了该强非线性系统在外部简谐位移激励下的稳态响应特征[12-15]。并通过直接数值方法加以验证。研究发现增加线性弹簧振子，能够有效的改变磁力悬浮的非线性振动能量采集器的动力学响应，并进一步提高能量采集的强度和带宽。通过对比不同参数的系统响应，研究了系统各参数对能量采集效果的影响。

1　磁悬浮非线性能量采集系统建模

磁悬浮振动型能量采集系统工作原理见图1和图2，两个磁体固定在支柱上的两端，支柱中间再插进一磁体，其下方悬挂一个弹簧振子。上下磁体两极的磁力使中间磁体可以悬浮在中间。当该系统在外部谐波激励下，中间磁体就产生非线性振动，并且改变Terfenol-D/PZT/Terfenol-D层压复合材料的周围磁场。由于Terfenol-D具有磁振效应，Terfenol-D的形状被改变。Terfenol-D和PZT足够牢固造成PZT也随着振动。PZT具有压电效应，在PZT形状尺度的改变时就产生了电流。

图1　磁力悬浮能量采集系统图Fig.1 A illustration of the magnetic levitation energy harvesting system

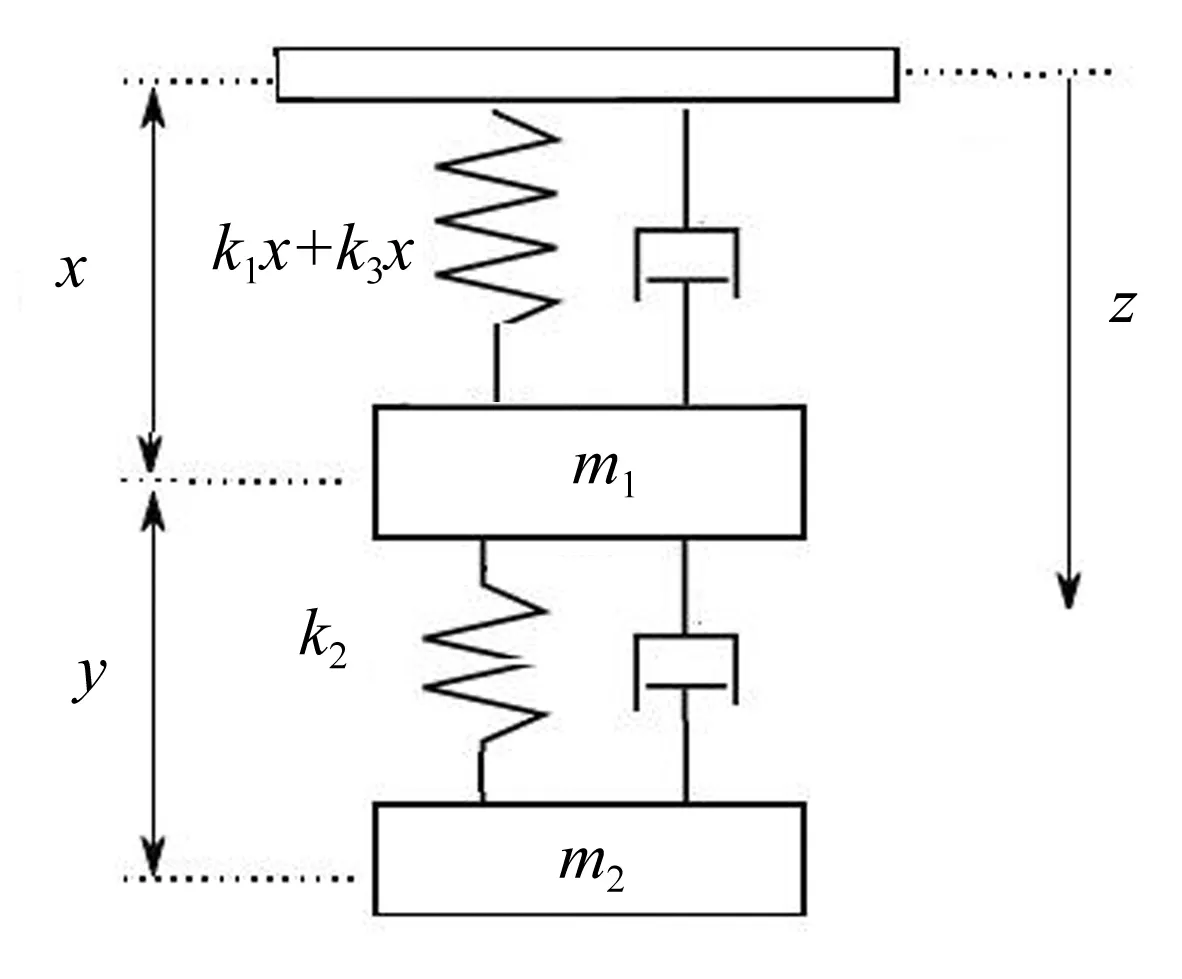
图2　磁力悬浮能量采集系统的力学模型图Fig.2 A mechanical model schematic of the magnetic levitation energy harvesting system

由于磁力的密度取决于中间磁体与两端磁体的距离，而距离的求解可以通过系统的控制方程得到。考虑非线性磁力、重力、阻尼和根据牛顿第二定律可以得到系统的运动方程:

(1)

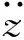
2　谐波平衡法分析

由于图1所示的能量采集装置是一个强非线性系统，这里通过谐波平衡法对式(1)进行近似求解。为了将分析的问题一般化，首先对式(1)进行无量纲化处理，即取如下所示无量纲参数

(2)

将以上无量纲参数代入控制方程式(1)，可以得到如下无量纲化的控制方程

(3)

假设式(3)的解满足如下形式

(4)

将式(4)代入式(3)，并令常数项cosωt和sinωt的系数分别相等，得到下列方程

a10+βa103+a1-μf2a20+

(5)

(1+μ)f2a20-a10-βa103-

(6)

μωfγ2a21-μf2b21-p=0

(7)

+μωfγ2b21-μf2a21=0

(8)

-ω2b21+(1+μ)fωγ2a21+

(1+μ)f2b21-γ1ωa11-b11-

(9)

-ω2a21-(1+μ)fωγ2b21+(1+μ)f2a21+γ1ωb11-

(10)

对于给定的激励频率ω，通过求解式(5)～式(10)，可以解得a10,a20,a11,a21,b11,b21。从而可以分别求得中间磁铁和弹簧振动的振幅，即

(11)

3　系统参数对幅频响应的影响

为研究新引入弹簧振子对磁力悬浮能量采集系统的幅频响应的影响，选取如下系统参数[10]:m1=0.012 g，c1=0.1 Ns/m，线弹性项系数k1=6.39 N/m，非线性弹性系数项k3=166 000 N/m3，外激励位移W=0.011 5 m，c2=0.01 Ns/m，弹簧系数k2=0.01 N/m，m2=0.012μg，其中μ是弹簧悬挂质量与中间磁铁的质量比值。

3.1二自由度的质量比的影响

接下来先运用谐波平衡法，计算在不同的质量比μ下磁力悬浮能量采集系统的幅频响应。如图2所示，当μ=0.05时，磁力悬浮能量采集系统的幅频响应类似单自由度的幅频响应，即仅存在一个共振峰。其原因是悬挂的振子质量过小，可以忽略不计。此时，中间磁铁的振动幅度在ω=2.0～2.5之间达到峰值。当μ=1和1.5时，中间磁铁的稳态响应振幅都在ω=1.0附近和ω=3.5附近时，出现两个共振峰。而且第二个共振峰的幅度超过了单峰时的共振幅度。另外，从图3可知，质量比越大，第一个共振峰的幅值越小，但是第二个共振峰的幅值同时在增大。还需要指出，质量比越大，两个共振峰之间距离越大。

图4给出μ=1时四阶龙格库塔法的直接数值结果与谐波平衡法近似分析结果的对比。观察发现，通过数值方法得到的中间磁铁的振幅与谐波平衡法得到中间磁铁的振幅基本吻合。

图3　在不同质量比下的中间磁体幅频频响应Fig.3 Frequency response of middle magnet as the mass ratio μ changes

图4　中间磁铁幅频响应的数值验证(质量比μ=1)Fig.4 Numerical verification for the frequency response of middle magnet as the mass ratio μ=1

3.2两自由度的频率比的影响

接下来研究两自由度系统前两阶固有频率比值对磁力悬浮能量采集系统能量采集效果的影响。选取质量比的μ=1。为了方便起见，选取固有频率比的平方分别为6、9和16。在选取频率比和其他参数的条件下，可以求得悬挂弹簧线弹性系数k2。

如图5所示，当频率比的平方比取为9时，中间磁铁稳态幅频响应的第一个共振峰幅值要比频率平方比取为6和16时的第一个峰值大，与此同时，第二个共振峰的峰值要比其他的峰值小。因此，可以通过调节两自由度之间的频率比，改变共振区域和强度，并到达强化某一阶主共振的目的。从而提高系统对振动能量采集的效果。

图5　中间磁铁在不同频率比的平方下的幅频频响应Fig.5 Frequency response of middle magnet as the tuning square ratio f changes

3.3非线性系数的影响

选取两自由度质量分别为m1=0.012 g和m2=0.012 g。并选取非线性弹性系数k3=166 000 kN/m3。图6给出了k取为1、6和10时，中间磁铁的稳态幅频响应曲线。观察图6发现，非线性弹簧系统的取值对第一阶主共振的位置影响不大，但是非线性系统较小时，第一阶共振峰的峰值较高。另一个方面，非线性系统对第二阶共振的影响更为显著，不但会影响共振区域，较大的非线性系数还会增强第二阶共振峰峰值。

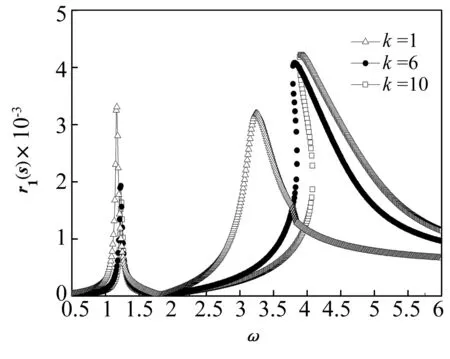
图6　中间磁铁在不同的非线性系数比k下的幅频响应Fig.6 Frequency response of middle magnet as the nonlinear coefficient ratio k changes

4　结　论

通过在已存在的一种磁力悬浮非线性能量器采集系统中增加一个线性弹簧振子，本文的研究表明，新增振子能够很大程度上改变系统的动力学特性。通过受力分析建立两自由度的非线性振动控制方程。通过谐波平衡法的近似解析分析和直接数值方法的验证研究了该能量采集系统在简谐位移激励下的稳态辐频响应。研究表明，系统的响应从单共振峰演化为该单峰两边的两个共振峰，因此增大了能量采集的频带宽度。另外，通过参数分析发现，调节系统参数，可以方便的增强两个共振峰的中任意一个，以达到增强振动能量采集效果的目的。

[1] 胡长德, 赵美蓉, 刘颖伟,等. 压电微悬臂梁共振频率的检测系统[J]. 压电与声光, 2009, 31(6): 935-938.

HU Changde,ZHAO Meirong, LIU Yingwei, et al.Resonance frequency detection of piezoelectric micro-cantilever[J]. Piezoelectrics & Acoustooptics,2009, 31(6): 935-938.

[2] 袁江波,谢涛,陈维山,等. 悬臂梁压电发电装置的实验研究[J]. 振动与冲击, 2009, 28(7): 69-72. YUAN Jiangbo, XIE Tao, CHEN Weishan,et al. Experimential study on piezoelectric generator with cantilever [J]. Journal of Vibration and Shock, 2009, 28(7): 69-72.[3] 陈仲生, 杨拥民. 悬臂梁压电振子宽带低频振动能量俘获的随机共振机理研究[J]. 物理学报, 2011, 60(7): 074301.

CHEN Zhongsheng, YANG Yongmin. Stochastic resonance mechanism for wide band and low frequency vibration energy harvesting based on piezoelectric cantilever beams [J]. Acta Physica Sinica, 2011, 60(7): 074301.

[4] 刘海利, 徐天柱, 黄震宇, 等. 基于谐振器的多模态压电换能结构研究[J]. 振动工程学报,2011,24(5):491-497.

LIU Haili, XU Tianzhu, HUANG Zhenyu, et al.A piezoelectric cantilever with an oscillator for multi-mode vibration energy harvesting [J]. Journal of Vibration Engineering, 2011, 24(5): 491-497.

[5] DAI Xianzhi, WEN Yumei, LI Ping, et al. Modeling characterization and fabrication of vibration energy harvester using Terfenol-D/PZT/Terfenol-D composite transducer [J]. Sensors and Actuators, 2009, 156: 350-358.

[6] JIANG Wenan, CHEN Liqun. Energy harvesting of monostable Duffing oscillator under Gaussian white noise excitation [J]. Mechanics Research Communications, 2013, 53: 85-91.

[7] ZHOU Shengxi, CAO Junyi, INMAN D J, et al. Broadband tristable energy harvester: modeling and experiment verification [J]. Applied Energy, 2014, 133: 33-39.

[8] WU Z, HARNE R L, WANG K W. Harvester synthesis via coupled linear-bistable system with multistable dynamics [J]. Journal of Applied Mechanics,2014,81:0610051-0610059.

[9] JIANG Wenan, CHEN Liqun.Snap-through piezoelectric energy harvesting [J]. Journal of Sound and Vibration, 2014, 333(18): 4314-4325.

[10] ZHU Yang, ZU J W, GUO L. A magnetoelectric generator for energy harvesting from the vibration of magnetic levitation [J]. IEEE Transactions on Magnetics,2012,48(11):3344-3347.

[11] MANN B P, SIMS N D. Energy harvesting from the nonlinear oscillations of magnetic levitation [J]. Journal of Sound and Vibration, 2009, 319: 515-530.

[12] 陈立群, 吴哲民. 多自由度非线性振动分析的平均法. [J].振动与冲击,2002,21(3):63-65.

CHEN Liqun, WU Zhemin. Averaging method for analyzing a multi-degrees of freedom[J]. Journal of Vibration and Shock, 2002, 21(3): 63-65.

[13] 黄坤, 冯奇. 非对称截面两自由度非线性振动[J]. 振动与冲击, 2012, 31(8): 80-85.

HUANG Kun, FENG Qi. Non-linear vibration of two-degree-freedom for a non-symmetrical cross-section[J]. Journal of Vibration and Shock, 2012, 318(8): 80-85.

[14] 胡辉, 郭源君, 郑敏毅.一个非线性奇异振子的谐波平衡解[J]. 振动与冲击, 2009, 28(2): 120-123.

HU Hui, GUO Yuanjun, ZHENG Minyi. Harmonic balance approaches for a non-linear singular oscillator[J]. Journal of Vibration and Shock, 2009, 28(2): 120-123.

[15] 贾尚帅, 孙舒, 李明高. 基于谐波平衡法的双稳态压电发电系统非线性振动特性研究[J]. 振动与冲击,2014,33(6): 170-173.

JIA Shangshuai, SUN Shu, LI Minggao. Non-linear vibration analysis of bistable piezoelectric power generation system based on harmonic balance method[J]. Journal of Vibration and Shock, 2014, 33(6): 170-173.

Nonlinear oscillations of a two-degree-of-freedom energy harvester of magnetic levitation

WANG Zuyao1,2, DING Hu1, CHEN Liqun1,3

(1. Shanghai Institute of Applied Mathematics and Mechanics, Shanghai University, Shanghai 200072, China;2. School of Science, Zhejiang University of Science and Technology, Hangzhou 310023, China;3. Department of Mechanics, Shanghai University, Shanghai 200444, China)

For enlarging the area of magnetic levitation nonlinear energy harvesting, the paper studied the nonlinear dynamics of a two-degree-of-freedom nonlinear energy harvester of magnetic levitation for the first time. A one-degree-of-freedom nonlinear energy harvester of magnetic levitation was expanded by introducing an linear oscillator. The nonlinear ordinary differential equations were approximately analyzed by using the harmonic balance method. Under the displacement excitation, the characteristics of the steady-state amplitude-frequency response of the primary resonance was studied. The results show that the resonance area of the two-degree-of-freedom system is significantly expanded. Moreover, by comparing the various parameters on the amplitude-frequency response and the resonance area, the effects of the mass ratio, frequency square ratio and nonlinear coefficient ratio on resonance are investigated. Therefore, the influences of the intensity of energy acquisition and the bandwidth are determined. In addition, the approximate analytic results are verified through a direct numerical simulation.

nonlinearity; vibration; magnetic levitation; energy harvesting; harmonic balance

国家自然科学基金重点项目(11232009); 国家自然基金面上项目(11372171); 国家自然基金优青项目(11422214)

2015-06-23修改稿收到日期：2015-08-28

王祖尧 男，博士生，1969年生

丁虎 男，博士，教授，博士生导师，1978年生E-mail: dinghu3@shu.edu.cn

O322

A

10.13465/j.cnki.jvs.2016.16.010