地震作用下结构拟静力分量对车桥系统动力响应的影响分析

杜宪亭, 乔　宏, 夏　禾, 王少钦, 李　啸

(1. 北京交通大学 土木建筑工程学院 北京　100044；2. 北京建筑大学 理学院 北京　100044)



地震作用下结构拟静力分量对车桥系统动力响应的影响分析

杜宪亭1, 乔宏1, 夏禾1, 王少钦2, 李啸1

(1. 北京交通大学 土木建筑工程学院 北京100044；2. 北京建筑大学 理学院 北京100044)

在地震易发区域当地震发生时桥上正行驶列车的概率越来越大，然而地震作用下结构拟静力分量对于车桥系统动力响应影响的研究不足。将桥梁、车辆分别简化为等截面简支梁、簧上质量系统，建立耦合振动系统在多点地震作用下运动方程，将桥梁结构动力响应分解，推导出拟静力分量影响的精确表达式。在此基础上，给出耦合振动系统求解流程。以簧上质量系统通过32 m简支梁遭遇地震作用为例，进行结构拟静力分量影响规律研究。分析结果表明：①地震作用下车桥耦合振动分析考虑结构拟静力分量的影响需要输入地震位移、速度、加速度时程；②相对于桥梁子系统，结构拟静力分量对簧上质量系统影响较大，最大到16%，且该影响对于车速更加敏感；③忽略结构拟静力分量可能造成车桥动力分析结果出现较大偏差，这与结构抗震分析显著不同。

车桥系统；地震动；结构拟静力分量；伯努利-欧拉梁；簧上质量

随着高速和城际铁路的快速发展，桥梁在线路中的比例不断增加；地震发生时桥上正行驶列车的概率越来越大。地震激励作用下车桥耦合系统的动力响应问题成为了研究的热点[1-4]。

借鉴传统桥梁抗震分析方法[5]，既有研究多将桥梁动力响应分解为拟静力分量和拟动力分量，忽略了拟静力分量的影响[6-8]。然而，地震作用下的车桥耦合振动分析不是传统桥梁地震响应分析与车桥耦合振动分析的简单叠加。在桥梁抗震分析中，结构安全性是研究重点，关注系统的相对运动；而车桥耦合振动分析关注行车安全性，涉及到系统的绝对运动。因此，研究地震激励下结构的拟静力分量对车桥系统动力响应的影响具有重要意义。

本文将桥梁、车辆分别简化为等截面简支梁、簧上质量系统，建立耦合振动系统在多点地震作用下的运动微分方程，将桥梁结构动力响应分解，推导出拟静力分量对系统动力响应影响的解析表达式。采用时域形式的高通滤波器对实测地震加速度时程进行处理，得到满足一致化要求的地震记录。在此基础上，给出了基于Newmark-β积分方法的耦合振动系统动力响应求解流程。最后，以簧上质量通过32 m简支梁时遭遇地震作用为例，研究了结构拟静力分量的影响规律。

1　分析模型

1.1模型参数

本研究讨论简支梁和移动车轮(质量)+弹簧(阻尼器)+簧上质量体系的地震反应，见图1。

地震波从简支梁A端传向B端，两端分别遭遇不同的竖向地震动a(t)、b(t)作用。通过简支梁的列车被简化为一系列不等间距的簧上质量振子；而簧上质量振子由下质量块M1(移动车轮)、上质量块M2、弹簧K1和阻尼器C1组成。设梁的动挠度为u(x,t)，上质量M2的动位移为Z(t)，假定下质量块M1沿梁长移动而不脱离开梁体，则其位移由它所在位置的梁的挠度以及轨道不平顺迭代得到[9]。

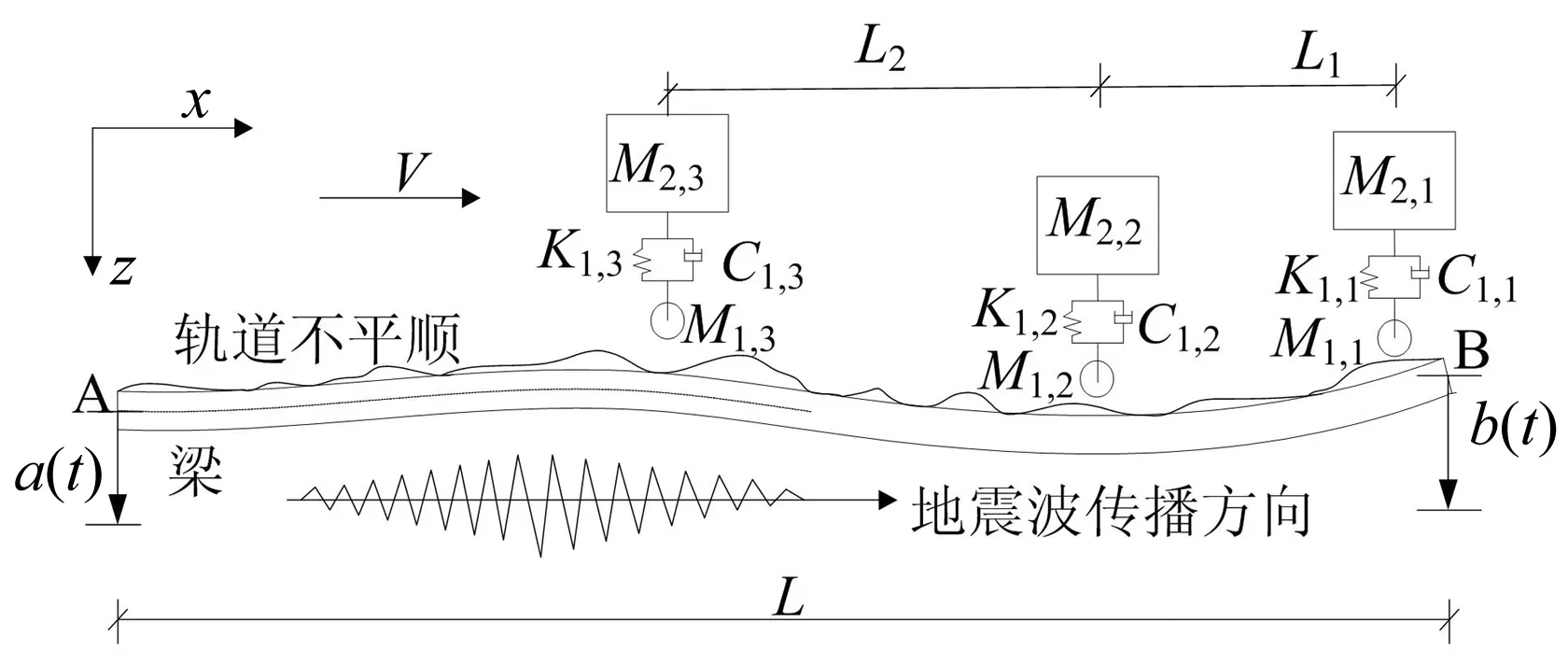
图1　簧上质量通过简支梁遭遇地震Fig.1 Vehicle-bridge system subjected to seismic ground motion

1.2系统运动方程

将简支梁简化为Rayleigh阻尼的Bernoulli-Euler梁，相应的运动可以由微分方程来表达[10]。假定列车以不变的速度V通过桥梁。系统的受力分析见图2。作用于梁的荷载有下质量块M1的惯性力FI、移动质量的重力FG、弹性力FS、阻尼力FD；作用到上质量块的荷载有惯性力PI2、弹性力Ps=Fs、阻尼力PD=FD。

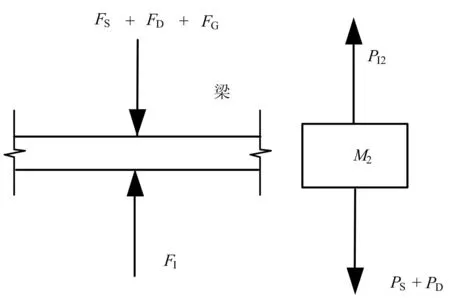
图2　受力图Fig.2 Force diagram

这样，遭遇多点地震激励的车桥耦合系统的控制运动方程可以由下列两式表达：

K1,i[Z2,i(t)-u(x,t)-ZIR]+

(1)

(2)

式中：

(3)

(4)

(5)

简支梁的边界条件通过下式表达[10]：

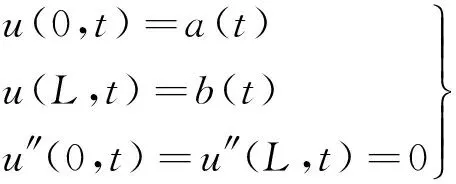
(6)

将简支梁的响应分解为拟静力项和动力项：

u(x,t)=us(x,t)+ud(x,t)

(7a)

(7b)

(7c)

式中：下标s、d分别代表拟静力分量、动力分量；固有模态un(x)通过广义坐标qn(t)来衡量其对动力分量的贡献；拟静力分量us(x,t) 满足下式：

EIu″″s(x,t)=0

(8)

同时又有下列边界条件：

us(0,t)=a(t)；us(L,t)=b(t)

(9a)

u″s(0,t)=u″s(L,t)=0

(9b)

式(8)的解为：

(10)

u(x,t)对时间的一阶、二阶导数变为：

(11)

(12)

将式(11)、(12)代入式(1)，整理得到：

EIu″″d(x,t)=Fd+Fs

(13)

式中：Fd、Fs分别为作用到梁上的动力相互作用项、拟静力附加作用项：

(14)

Fs=

(15)

(16)

(17)

(18)

(19)

类似地，式(2)变为：

(20)

式中：Pd和Ps分别为作用到上质量块的动力相互作用项、拟静力附加项。

(21)

(22)

(23)

(24)

特征函数的正交性满足下式：

m,n=1,2,…

(25)

将式(7b)、(7c)代入式(1)左端，在方程两端同时乘以um(x)，然后在(0，L)范围内进行积分，再利用振型的正交特性得到：

(k=1,2,…)

(26)

式中：

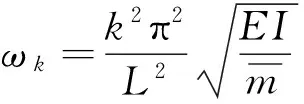
(27)

u″d(x,t)V2]+K1,i[Z2,i(t)-ud(x,t)]+

(28)

(29)

(30)

(31)

(32)

(33)

当简支梁A、B两端的地震动完全相同时，即为一致地震激励的情况，这时有a(t)=b(t)，作用到上质量块的拟静力附加项变为：

(34)

而作用到简支梁上的拟静力附加项变为：

(35)

从式(34)、(35)不难看出，地震加速度为零时，其位移和速度并不一定等于零，依然可能通过弹簧和阻尼器产生作用到耦合系统上的地震力。因此，在考虑一致地震激励时，依然需要同时输入地震动的位移、速度、加速度时程。

2　地震一致化处理方法

如前所述拟静力项对车桥耦合动力系统的影响不可忽略，而拟静力分量包含了位移、速度、加速度三个分量。这与传统桥梁抗震分析仅仅输入地震加速度有着显著不同。

然而实测地震记录或者人工地震波多为加速度时程形式。由于加速度时程中包含了各类噪声、误差的影响，若直接对其进行积分得到速度、位移时程，会产生误差较大的趋势线，不能直接用于地震作用下的车桥耦合动力分析[11]。因此，需要先对地震波加速度时程进行修正，去除其中所含误差，进而得到一致化的地震加速度、速度和位移时程。

本研究采用时域内高通滤波法。时域内高通滤波法使用临界阻尼振子形式的高通滤波器对地震加速度时程进行修正，进而得到满足一致化要求的地震记录[12]。具体实现可以通过求解下列微分方程完成：

(36)

式中：u代表位移向量；下标o、b分别代表修正前与修正后桥梁支撑处的地面运动；ωc为滤波器角频率。

3　数值求解流程

式(20)、(26)构成了系统的基本运动方程，可以通过数值积分方法求解。具体步骤如下：

步骤1输入总体控制参数，如时间积分步长Δt、簧上质量系行走速度V等。

步骤2输入簧上质量系统信息，建立簧上质量系统子系统动力平衡方程，并设置初始条件。

步骤3输入简支梁信息，建立桥梁子系统模态动力平衡方程，形成等效刚度矩阵，设置初始条件。

步骤4输入轨道不平顺，计算不平顺速度、加速度。

步骤5输入地震记录时程。

步骤6给定时间步，使用Newmark-β法迭代求解车桥耦合系统动力响应，主要涉及以下过程：① 确定簧上质量在桥梁上的位置;② 计算簧上质量处轨道不平顺、不平顺速度及加速度、各阶桥梁模态值;③ 计算簧上质量子系统源于上一步的等效力以及作用到上质量块上的拟静力附加作用项;④ 计算桥梁子系统源于上步的等效力以及作用到梁上模态形式的拟静力附加作用项;⑤ 计算作用到上质量块的动力相互作用项,计算簧上质量系的动力响应;⑥ 计算作用到梁体上的动力相互作用项计算梁体的动力响应;⑦ 收敛判断是否收敛。若收敛则更新耦合系统运动状态，输出时间步结果；若不能收敛则重复步骤④～⑦。判断收敛的标准依据两个子系统的力、位移向量的范数：

(37)

式中：E为允许的相对误差，F、u分别为两个子系统的作用力、位移向量，下标i、i-1分别为当前、上一步的迭代。

4　算例

选取铁路32 m双线整孔简支箱梁作为研究对象。梁的一阶频率为4.72 Hz，每延米质量为28.14 t，Rayleigh阻尼系数α、β分别取为0.138 s-1、0 s。分析只选取一个簧上质量系统，其上、下质量块的值分别取为13.6 t、2.4 t。联结弹簧K1和阻尼器C1分别取为2.08 MN/m、100 kN·s/m。分析时，考虑了轨道不平顺的影响，见图3。质量系统的运行速度在V=80～90 m/s之间。

图3　轨道竖向不平顺Fig.3 Vertical irregularity curve

借助于时域高通滤波器对实测地震加速度时程进行了一致化和规格化处理，得到的地震记录见图4，相应的加速度峰值为0.05 g。

图4 　一致化地震记录Fig.4 Consistent earthquake record

图5、图6分别给出了地震初始作用3.0 s时列车入桥且车速V=80 m/s条件下桥梁跨中位移时程、上质量块加速度时程。通过对比分析不难发现，考虑结构拟静力分量一定程度上改变了车桥耦合振动峰值出现的时间和大小。

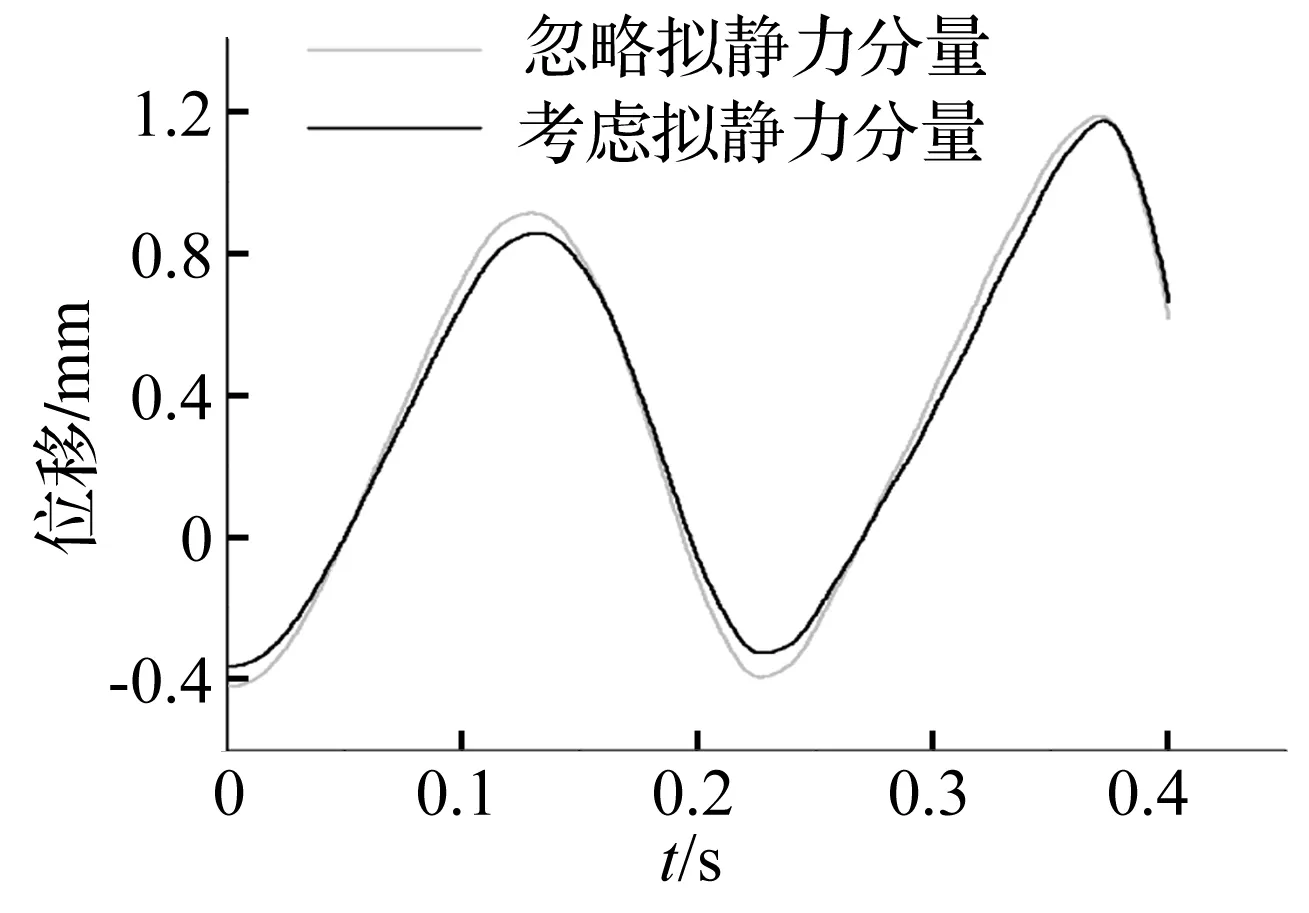
图5　桥梁跨中位移时程Fig.5 Displacement time histories of the bridge at mid-span

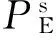
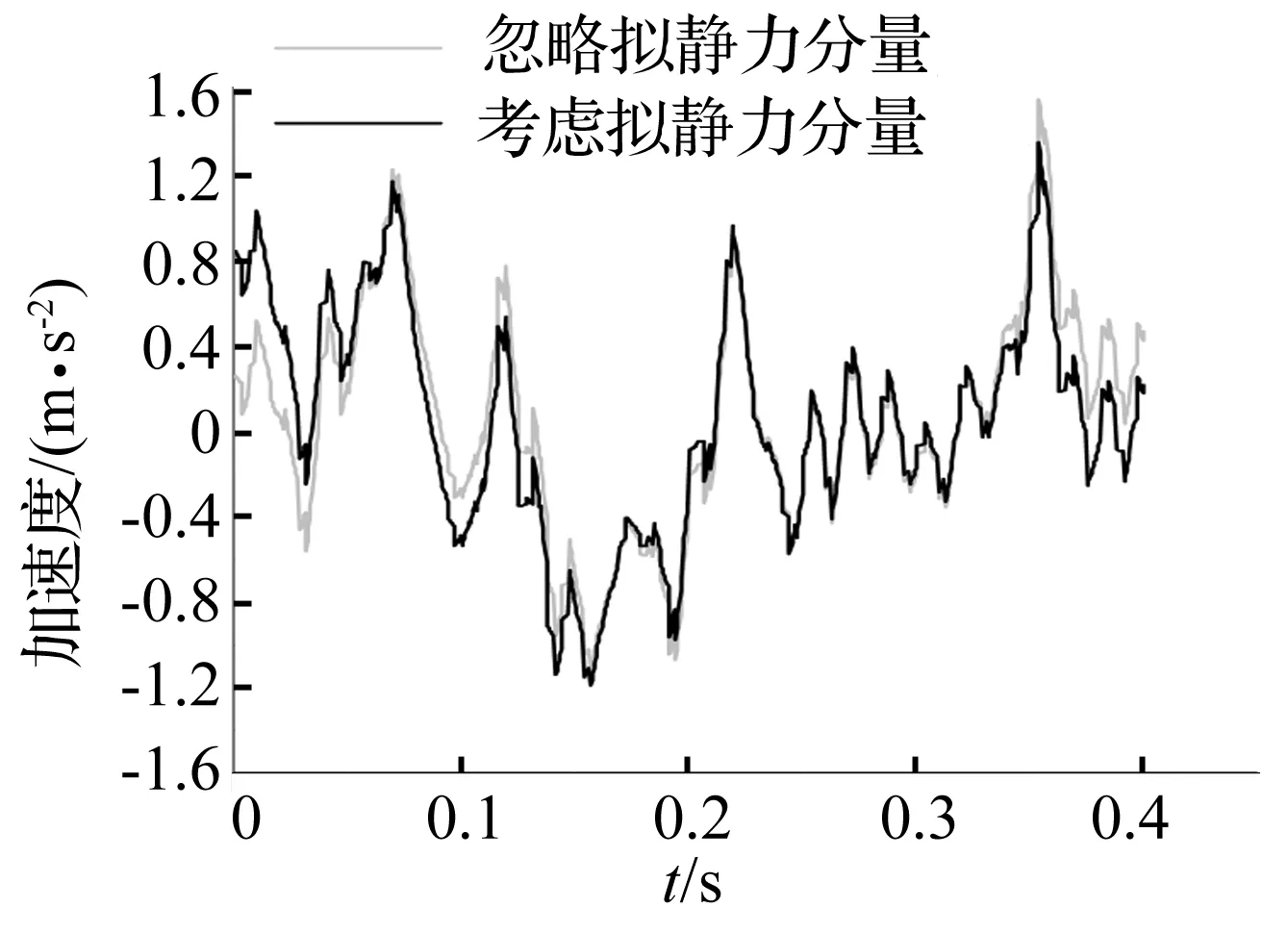
图6　上质量块加速度时程Fig.6 Acceleration time histories of sprung mass

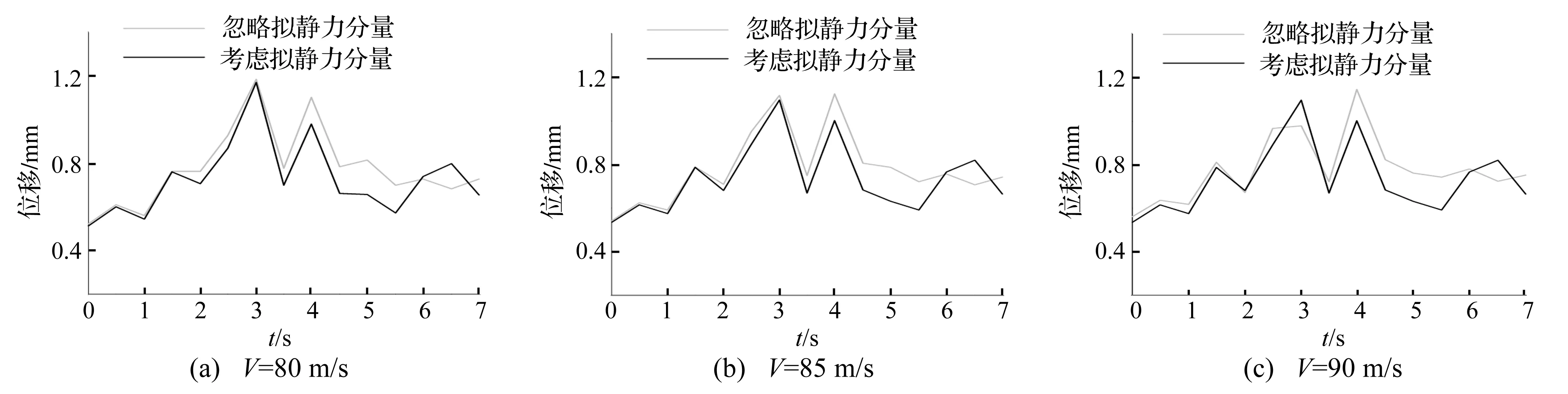
图7　拟静力分量对桥梁位移最大值影响Fig.7 Influence of pseudo static component of seismic excitation on maximum bridge displacement

5　结　论

基于上述理论分析及数值算例结果，可以得出如下结论：

(1) 地震作用下车桥耦合振动分析考虑结构拟静力分量的影响需要输入地震位移、速度、加速度时程；

(2) 相对于桥梁子系统，结构拟静力分量对簧上质量系统影响较大，最大到16%，而且该影响对于车速更加敏感；

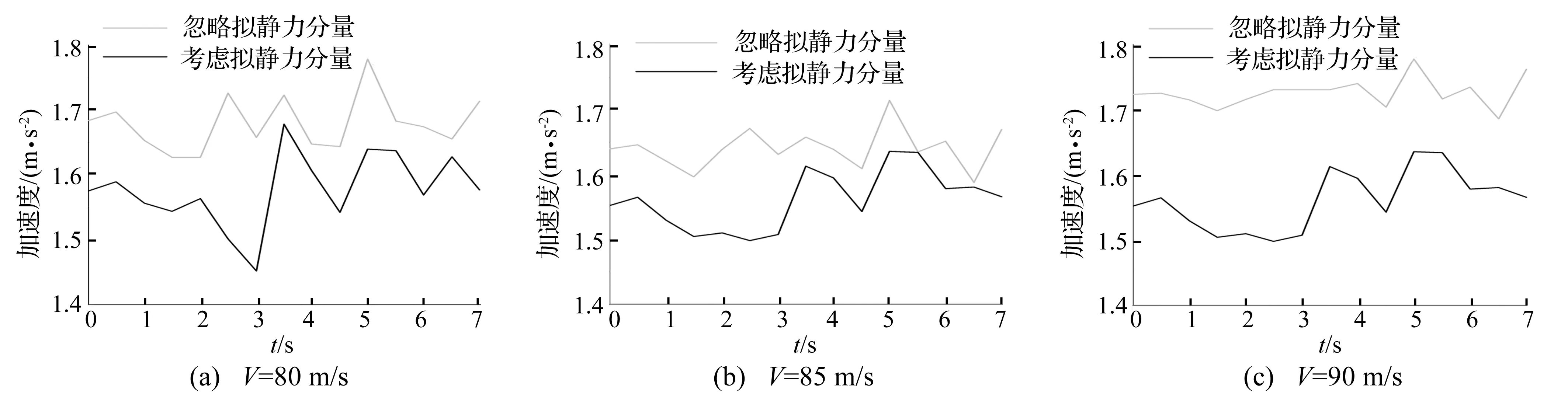
图8　拟静力分量对上质量块加速度最大值影响Fig.8 Influence of pseudo static component of seismic excitation on maximum bridge displacement

(3)忽略地震作用下结构拟静力分量可能造成车桥动力分析结果出现较大偏差，这与结构抗震分析显著不同。

上述结论针对二维车桥模型分析得出，没有考虑水平地震动的影响。而在实际工程中水平地震动也可能控制桥上列车的行走安全性，这需要建立更加复杂、精确的数值分析模型。

[1] XIA He, HAN Yan, ZHANG Nan, et al. Dynamic analysis of train-bridge system subjected to non-uniform seismic excitations [J]. Earthquake Engineering and Structural Dynamics, 2006, 35: 1563-1579.

[2] DU X T, XU Y L, XIA H. Dynamic interaction of bridge-train system under non-uniform seismic ground motion [J]. Earthquake Engineering and Structural Dynamics, 2012,41(1): 139-157.

[3] 谭长建, 祝兵. 地震作用下高速列车与桥梁耦合振动分析[J]. 振动与冲击, 2009, 28(1): 4-8.

TAN Changjian, ZHU Bing. Coupled vibration analysis of high speed train and bridge subjected to seismic excitation [J]. Journal of Vibration and Shock, 2009, 28(1): 4-8.

[4] 杜宪亭, 夏禾, 余竹. 车桥耦合动力分析中地震动输入模式的研究[J]. 中国铁道科学, 2011, 32(6):34-40.

DU Xianting, XIA He, YU Zhu. Study on the input patterns of seismic ground motion in the dynamic interaction analysis of train-bridge system [J]. China Railway Science, 2011, 32(6):34-40.

[5] CHOPRA A. Dynamics of structure [M]. New Jersey: Prentice-Hall, 1995.

[6] 熊建珍, 高芒芒, 俞翰斌. 天兴洲长江大桥斜拉桥在地震作用下的车-桥耦合振动分析 [J]. 中国铁道科学, 2006, 27(5): 54-59.

XIONG Jianzhen, GAO Mangmang, YU Hanbin. Vehicle-bridge coupling vibration analysis of cable-stayed bridge of Tianxingzhou Yangtze River Bridge under earthquakes [J]. China Railway Science, 2006, 27(5): 54-59.

[7] 韩艳, 夏禾, 郭薇薇. 斜拉桥在地震与列车荷载同时作用下的动力响应分析 [J]. 工程力学,2006,23(1):93-98.

HAN Yan, XIA He, GUO Weiwei. Dynamic response of cable-stayed bridge to running trains and erathquakes [J]. Engineering Mechanics, 2006, 23(1): 93-98.

[8] 王少林, 翟婉明. 地震作用下高速列车-线路-桥梁系统动力响应[J]. 西南交通大学学报, 2011(1): 56-62.

WANG Shaolin, ZHAI Wanming. Dynamic response of high-speed train-track-bridge system under seismic excitations [J]. Journal of Southwest Jiaotong University,2011(1):56-62.

[9] 夏禾, 张楠. 车辆与结构动力相互作用[M].2版. 北京: 科学出版社, 2005.

[10] CHEN J T, HONG H K, YEH C S, et al. Integral representations and regulations for a divergent series solution of a beam subjected to support motions [J]. Earthquake Engineering and Structural Dynamics, 1996, 25: 909-925.

[11] 谢礼立,于双久.强震观测与分析原理[M].北京:地震出版社,1982.

[12] 杜宪亭, 夏禾. 地震空间变异性对车桥系统响应的影响分析[J]. 工程力学, 2012, 29(9): 106-111.

DU Xianting, XIA He. Influence of spatial vibration of seismic ground motion on dynamic response of train-bridge system [J]. Engineering Mechanics,2012,29(9):106-111.

Influence of structure quasi-static components on the dynamic response of train-bridge systems during earthquakes

DU Xianting1, QIAO Hong1, XIA He1, WANG Shaoqin2, LI Xiao1

(1. School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China;2. School of Science, Beijing University of Civil Engineering and Architecture, Beijing 100044, China)

In regions prone to earthquakes, the possibility of trains running on bridges when an earthquake occurs is high. However, the influence of structure quasi-static components on the seismic response of train-bridge systems has not been well studied. In this paper, a bridge subsystem and the train subsystem were simplified as a simply-supported beam with a uniform cross-section and a moving vehicle with a wheel(unsprung-mass), a spring, a damper, and a sprung-mass, respectively. Then the motion equations of the train-bridge coupling system subjected to multi-support seismic excitations could be obtained. The influence of structure quasi-static components could be expressed precisely by decomposing the dynamic response of the bridge subsystem and then the solving procedures were proposed. A moving vehicle with a wheel(unsprung-mass), a spring, a damper and a sprung-mass passing through a 32 m simply-supported beam was taken as a case study, in which the influence rule of structure quasi-static components was analyzed. The results show:(1) in the dynamic analysis of the train-bridge system subjected to earthquake actions considering the influence of quasi-static components, it is necessary to input the displacement, velocity as well as acceleration time history of ground motion;(2) compared with the bridge subsystem, quasi-static components have more influence on the train subsystem, which is as high as 16% and sensitive to the train speed;(3) neglecting the quasi-static components may lead to large deviation responses of the coupled system, which differs greatly from the aseismatic analysis of bridges.

coupled train-bridge system; seismic ground motion;structure quasi-static components; Bernoulli-Euler beam; sprung-mass system

国家自然科学基金项目(51208027);973计划项目(2013CB036203);中央高校基本科研业务费专项资金资助项目(2014JBM092)

2015-05-28修改稿收到日期：2015-08-21

杜宪亭 男，博士，副教授，1978年5月生

夏禾 男，硕士，教授，博士生导师，1951年4月生

U24

A

10.13465/j.cnki.jvs.2016.16.002