基于误差估计的发动机排气声源特性间接识别模型求解方法研究

刘海涛， 连小珉， 刘林芽

(1.华东交通大学 机电与车辆工程学院，南昌　330013； 2.清华大学 汽车安全与节能国家重点实验室，北京　100084)



基于误差估计的发动机排气声源特性间接识别模型求解方法研究

刘海涛1，2， 连小珉2， 刘林芽1

(1.华东交通大学 机电与车辆工程学院，南昌330013； 2.清华大学 汽车安全与节能国家重点实验室，北京100084)

用于发动机声源特性识别的线性时不变频域模型仍然是较为实用的方法，但尚存在求解误差大、对输入误差敏感、识别及求解过程复杂等问题。为了提高声源识别的准确性，建立了间接法声源特性识别的误差估计方法，即声源声压离散度估计和声源阻抗值偏差估计。将识别模型中超定非线性方程组中的方程式进行两两组合，通过解析几何的方法直接求解方程组，获得声源特性参数的多个解，再利用声源阻抗值偏差估计选取最优解。经分析计算，获取的声源特性参数的误差估计值要明显低于传统四负载法。最后，采用三维声流耦合仿真方法对获取的声源特性参数进行验证，仿真预测的远场响应点声压值与试验结果吻合良好，表明基于误差估计的声源特性参数最优选取法可以获取更加准确的发动机声源特性参数，减少识别误差和识别的复杂程度。

发动机；声源声压；声源阻抗；误差估计；声流耦合仿真

排气系统的性能与发动机的特性密切相关，二者之间存在流体耦合和声学耦合。流体耦合决定了发动机的排气功率损失，而声学耦合决定了尾管阶次噪声辐射能量的大小。为了更加有效的控制阶次噪声，需要准确提取出发动机声源特性参数，用于发动机和排气系统的匹配分析[1-2]。

国内外学者在发动机声源特性识别模型上做了大量的研究工作。有些学者将发动机定义为时变模型，在时域内计算发动机的声源特性参数[3-4]。时变模型能够考虑发动机排气产生的高声压级脉动的非线性效应，能够更好地描述发动机气缸和排气系统之间复杂的相互作用。时域计算模型需要获取发动机气缸及相关附件的准确几何参数，以及发动机的性能参数，如缸内压力、气门升程、点火提前角等，但这些关键性能参数在实际排气系统设计匹配工作中较难获取[5]。

发动机声源特性的线性频域识别模型仍然在排气系统的匹配设计中发挥重要作用[1,5]。线性频域识别模型将发动机简化成线性时不变系统，通过声电类比模型，可以将发动机的声源特性用声源声压和声源阻抗两个参数来描述[6]。国内外学者提出了许多方法来确定两个声源特性参数，主要可分为直接法和间接法两种。直接法[6-8]测试时需要外部声源激励来获取源特性参数，但难以找到能够耐受发动机排气管内极其恶劣环境的外部声源，因而直接法的应用受到限制。间接法不需要外部声源，只需要更换源特性识别负载测管，并获取尾管口远场辐射噪声即可，因而间接法在发动机声源特性识别中得到广泛应用。经过多年发展，间接法发展出了多种方法，如双负载法[9]，三负载法[10]，四负载法[11]以及多负载法[12-13]，这些方法都有各自的优缺点。双负载法需要一个与噪声产生过程相关的参考信号来计算复声压，但是这种参考信号不太容易选取。三负载法需要求解含有两个二元二次方程的方程组，由于测试误差以及模型简化的影响，可能在某些频率点下方程组的解不存在，从而限制了这种方法的应用。四负载法成功地避免了三负载法没有解的情况，也是国内外学者研究最多的一种方法。四负载法可以得到含有三个二元二次方程的非线性方程组，PRASAD[11]将方程组中的二次项消去，使得三个二元二次方程简化成两个线性方程，再联立求解获得发动机声源阻抗结果。但是经过国外学者SRIDHARA等[14]的研究，这种求解方法对于输入量引入的误差极其敏感，计算结果容易出现较大偏差。多负载方法通常测取十多个负载的尾管口辐射噪声，再采用最小二乘法[12]或者数值迭代[13]的方法对源特性参数进行数值求解，从一定程度上克服了传统四负载法计算结果不稳定的缺点，提高了识别精度。但是这种方法需要大量重复的发动机台架试验测试，并进行复杂的代数运算去求得源特性参数，会耗费大量的时间和精力，而且缺少对结果的定量误差分析。因而有必要研究更合理的声源特性参数求解方式，并进行定量的误差估计，以保证求解结果的准确性。

为了解决现有声源特性识别求解方法存在的问题，本文从声源特性识别误差估计出发，提出一种新的求解方法，相对于传统四负载法，在不增加测试负载数量的基础上提高声源特性参数的识别精度。

1　声源特性间接识别理论模型

线性频域求解模型将稳态工况下发动机排气噪声的产生假定成线性时不变系统，并将发动机简化成黑箱，用发动机声源声压和声源阻抗两个集总参数来表示发动机的声源特性。

1.1集总参数类比模型

如图1(a)表示典型发动机排气系统简化示意图。通过声电类比，发动机排气系统可以用恒压源电路来表示，如图1(b)所示。

图1　典型发动机排气系统及其声电类比示意图Fig.1 Typical engine exhaust system and its electroacoustic analogies

图1中，PE是源强度，ZE是源阻抗，PL是源与负载接口处的声压，ZL是负载阻抗，PR是距尾管口R处响应点的辐射声压，ZR是尾管口处的辐射阻抗，M表示排气系统入口处的气流马赫数，T表示排气系统入口处的温度。在频域识别模型中，源与负载之间的相互耦合作用可用式(1)表示。

PL=PEZL/(ZE+ZL)

(1)

对于内燃机，只有当声源特性测试中各个负载产生的背压相同或接近的时候，发动机的声源特性参数才不会随着测试负载的变化而产生较大的差异[5]，因而采用不同长度的直管作为声学负载会比较合理。另外直管负载方便使用和加工，而且标准直管的负载阻抗比较容易精确获取。对于不同长度的声源特性测管，式(1)可以改写成式(2)。

(i=1,2,3,…,N)

(2)

式中：i表示序数，N表示总共使用的测管数量。

对于直管声学负载，其进出口声学参数可使用四端极子参数联系起来，如式(3)所示。

(3)

式中：p是声压，U是体积速度；AL，BL，CL，DL分别是直管的四端极子参数。根据MUNJAL[15]推导的有流情况下管道内平面波的传播理论，四端极子参数可以由式(4)表示。

(4)

式中:M是气流马赫数，M=v/c，v是气流流速，c是管内声速；k是波数，k=w/c(1-M2)，Z0是管内气体的特征阻抗；le=L+Δl，L是测管长度，Δl是声学修正长度，采用热喷射流下的管道末端修正求得[16-17]。

发动机排气系统带有四端极子参数的线性频域类比模型图，如图2所示。

图2　带四端极子参数的发动机排气系统声电类比示意图Fig.2 Electrical analogue for source-load system with four pole parameters

图2可由传递矩阵方程式来表示，如式(5)所示。

(i=1,2,…,N)

(5)

式中：UE是发动机声源体积振速，Uo是测管末端的体积振速，ZR是有流情况下测管末端的辐射阻抗，可由式(6)[15]计算得到。

(6)

式中Rc是有流情况下尾管口的反射系数，可以通过MUNT[18]的理论计算得到，如式(7)所示。

(7)

式中:θ是反射系数的相位，θ=π-2kΔl；F+(u)是涡流层位置变换，式(7)的详细推导公式可参考文献[18]。

1.2声源阻抗的求解

在不同的负载情况下时，将式(2)表示各个负载的等式进行比值处理，消去声源声压|PE|，得到式(8)。

(m=1,2,…,N-1)

(8)

将源与负载接口处管内声压的比值换算到尾管外响应点辐射噪声声压的比值，再代入式(8)中，即可获取αm的值，如式(9)所示。

(m=1,2,…,N-1)

(9)

联立式(8)和式(9)，根据PRASAD的公式推导，可以得到用于声源阻抗求解的二元二次非线性方程组，如式(10)[11]所示。

(m=1,2,…,N-1)

(10)

式中：

ZE=RE+jXE

。

通过求解式(10)中的非线性方程组，可以获得发动机的源阻抗值。

1.3声源强度的求解

发动机声源特性的试验测量通常是在消声室中进行，以避免外界噪声环境的干扰。由于排气气流属于低马赫数流动，而且分析的频率范围位于低频段，忽略测管尾端喷射流中气流以及温度梯度对末端辐射噪声声传播的影响。测管管口的半径远小于传声器到尾管口端的距离，末端噪声辐射过程可以当作点声源来处理，末端远场辐射响应点的声强值可以由式(11)表示。

(k0r<1,i=1,2,…,N)

(11)

式中：ρ0和c0分别为消声室中空气的密度和声速，IR为响应点处的声强，可由式(12)来计算。

(12)

式中:PR是尾管末端远场辐射响应点传声器测量的声压。

将式(11)代入式(12)中，可以得到测管末端尾管口处的体积振速，如式(13)所示。

(13)

联立式(5)和式(13)可以获得声源声压PE和末端远场辐射响应点的声压PR之间的关系，如式(14)所示。

(i=1,2,…,N)

(14)

发动机的声源声压值可由式(14)计算得到。

2　间接识别模型的误差估计方法

2.1声源阻抗值偏差估计

由式(10)可知，当声源阻抗结果没有误差时，将其回代入声源阻抗求解方程组中，可以满足所有的方程。但当声源阻抗求解结果中带有误差时，式(10)中的方程等式右边将不再是零，而会出现一些偏差。而这个偏差可以用来估计声源阻抗求解结果的误差大小，并可以用来分析方程组中的参量，如测管的负载阻抗值ZL对声源阻抗识别结果的影响。

(m=1,2,…,N-1)

(15)

式(15)中可以看出，对于N个负载，将会产生N-1个偏差。为了方便统计偏差的大小，总的偏差可以由式(16)表示。

(16)

式中:E′t代表声源阻抗求解方程的偏差估计函数值，可以用来量化源阻抗求解结果的误差大小。

2.2声源声压值偏差估计

由式(14)可以看出，声源声压PE的结果主要由测管四端极子参数、测管末端辐射阻抗、声源阻抗以及末端远场辐射响应点声压决定。末端远场辐射响应点声压通过试验测试得到，其精度主要由试验环境和测试系统来保证。而测管四端极子参数、测管末端辐射阻抗、声源阻抗的误差将直接影响声源声压计算结果的精度。根据式(14)可知，每一个负载都可以计算出一个声源声压值，如果没有误差，则理论上所有负载对应的声源声压值都相同。但是当参与求解的参数存在误差时，每个负载计算出的声源声压值就会有偏差，而且误差越大，偏差值也会越大。因而每个负载计算出的声源声压值之间的离散度可以用来估计由测管四端极子参数、测管末端辐射阻抗、声源阻抗引入的误差大小，从而用于声源特性识别误差的分析。声源声压值的离散度可由式(17)表示。

(17)

式中:DPE表示声源声压值的离散度，而EPE表示各个负载求出的声源声压值的平均值，如式(18)所示。

(18)

声源声压值的离散度DPE可以用来估计声源特性识别模型中引入的误差大小，而EPE作为最终求解得出的声源声压值。

3　声源阻抗值最优选取求解方法

声源阻抗值的获取在于求解式(10)中的非线性超定方程组。传统四负载法是将非线性方程组经过替代转化成线性方程组，从而求解出声源阻抗值。但这种传统求解方法，会使得求解结果对于输入参数的误差极为敏感，容易产生极大的误差[14]。传统四负载法产生误差的核心问题是消除了式(10)中的二次项，因而本小节从这点出发，将超定非线性方程组中的方程式进行两两组合，通过解析几何的方法分别直接求解方程组，获得多个解，然后结合第2节中的偏差估计方法选取最优解，从而有效控制误差。

选用四种测管负载进行计算分析，则式(10)可写成方程组的形式，如式(19)所示。

(19)

从式(19)可知，非线性方程组从代数几何的角度来看，其实质是一系列圆方程。非线性方程组的解，就是这一系列圆的交点。当没有误差干扰时，三个圆将相交于一点，即声源阻抗值的精确解；而当有输入误差干扰时，三个圆方程将会有多个交点。选取式(19)中任意两个方程，通过解析几何的方法推导出交点的求解公式，两圆相交的几何示意图如图3所示。

图3　两圆相交的几何示意图Fig.3 Geometric diagram for the intersection of two circles

如图3所示，O1(ai/2,bi/2),O2(aj/2,bj/2)分别表示两个圆的圆心，其中i,j∈{1,2,3}。Ic(RE0,XE0)点是两圆心连线与两圆公共弦的交点，Is1(RE1,XE1),Is2(RE2,XE2)分别是两个圆的交点。

由两圆之间的平面几何关系可得到Ic的坐标，如式(20)所示。

(20)

式中:lo12为两个圆的圆心间距离，ro1和ro2分别为两个圆的半径。其中：

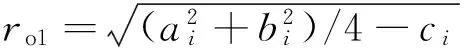
Is1和Ic之间的距离lcs可以由式(21)表示。

(21)

根据相交两圆的几何关系可以求得两圆交点的表达式，如式(22)和式(23)所示，式中Re表示取实部值。

(22)

(23)

联立以上等式，即可求解得到交点的坐标值。当两圆相交时，有两个交点；当两圆相切时，求出的两个交点的坐标值相同，即为一个交点；而当两圆相离时，求出的两个交点的坐标值是复数，这时没有几何意义上的交点。相离的情况下，应该取距离两圆最近的点作为圆方程的解，从而有效减小偏差。相离时式(22)和式(23)复数坐标点的实部值相同，构成的点位于圆心的连线上，处于两圆的中间，距离两圆是最近的点，因而将复数坐标点的实部值作为两圆的虚交点。

按对圆方程进行两两组合的求解方法，获得了多个交点，而选取其中误差最小的点作为发动机声源阻抗值是问题的关键。2.1小节中推导出了声源阻抗的误差估计方法，可以量化声源阻抗求解结果的误差大小。因而本文中以式(16)作为衡量标准，选取使偏差估计函数值最小的交点，可以用式(24)表示。

(24)

4　实际发动机声源特性参数求解分析

4.1试验装置

选用某款四缸汽油发动机进行声源特性识别试验。发动机台架采用电涡流测功机，负载测管以及响应点的传声器放置于半消声室中，同时在尾管口的地面上铺满吸声劈尖以减少地面的声反射，从而使测试环境接近于自由场。试验装置的示意图如图4所示。

图4　台架试验装置示意图Fig.4 Experimental set-up

响应点距离测管的尾管口500 mm，与尾管口的轴心线成45°夹角。为了防止尾管口喷射的热气流对传声器产生影响，在传声器的头部安装了风罩。试验现场的传感器布置照片如图5所示。

图5　测试装置现场实物图Fig.5 The photograph of test equipment

声压测量采用的是PCB公司生产的377C01型自由场传声器，可以用来测量高声压。而数据采集采用LMS公司生产的SCM02型数据分析仪。

采用了四个不同长度的直管当作声学负载用于发动机声源特性的测试。通过对压力传感器的信号进行分析发现，同一工况下，各种长度的直管负载所产的排气压力损失小于2 kPa，远小于排气系统中三元催化器的排气压力损失，因而不同直管负载所产生的背压对发动机源特性的影响可以忽略。四种不同长度的直管负载的几何参数如表1所示。

表1　试验测管几何参数

4.2声源特性参数计算分析

选取四个测管作为声学负载，根据线性频域源特性求解模型，其构成的三个圆方程的交点求解结果如图6所示。图6中，三个圆是由四个负载根据式(19)构成的，横轴是声源阻抗的实部，而纵轴是声源阻抗的虚部，并都进行了归一化处理。由于误差的存在，图中三个圆没有相交于一点，两个圆相交，另外一圆相离。图中的符号“*”标识出了三个圆所有的交点，包括相离情况下构成的虚交点。

图6　圆方程交点求解结果图Fig.6 The results of intersection points of circle equations

如图6所示，按对圆方程进行两两组合的求解方法，获得了多个交点，而选取其中误差最小的点作为发动机声源阻抗值是问题的关键。本文以式(24)作为衡量标准，选取使偏差估计函数值最小的交点，选取结果如图7(a)所示。图中的符号“*”标识出了求解结果。

图7　发动机声源特性参数求解结果Fig.7 The results of engine source impedance

图7(b)显示的是采用传统四负载法的求解结果。如图所示，按满足式(24)的阻抗值最优选取方法的计算结果基本位于三个圆接近相交的地方，而传统四负载方法的求解结果则偏离三个圆很远。图7充分说明，本小节提出的圆方程交点最优选取的求解方法能够有效控制输入误差对声源特性识别结果的影响。

按本文中提出的圆方程交点最优选取法和传统四负载法计算得到的发动机声源特性参数如图8所示。

图8　声源阻抗计算结果对比图Fig.8 The comparison of engine source impedance solved by the two methods

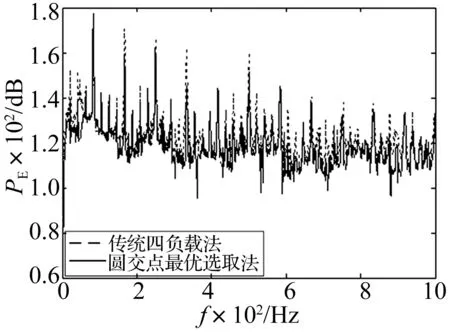
图9　声源声压计算结果对比图Fig.9 The comparison of engine source strength solved by the two methods

从图8看出，两种计算方式的声源阻抗结果存在一定的差异，传统四负载法的声源阻抗值波动明显较大。从图9可以看出，传统四负载法计算的声源声压值在阶次峰值处略要高于本文圆交点最优选取法的计算结果，另外在非阶次峰值处还存在较多的波动峰值。

将传统四负载法和本文提出的方法获取的声源阻抗结果分别代入式(16)和式(17)之中，可以获取两种方法求解结果的误差估计，如图10所示。

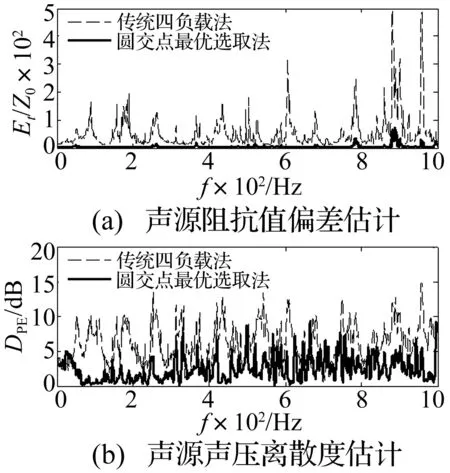
图10　两种求解方法结果的误差估计Fig.10 The error estimation of the results of two methods

求得的声源阻抗值偏差估计如图10(a)所示，声源声压离散度估计如图10(b)所示。从图10(a)可以看出，传统四负载法的阻抗值偏差估计结果在整个频带上都远大于圆交点最优选取法。图10(b)可以看出，传统四负载法的声源声压离散度估计值在全频带内也高于圆交点最优选取法，平均高出4 dB左右。

图7和图10充分说明，传统四负载法的求解结果偏差太大，准确性难以保证，而本小节提出的圆交点最优选取法，通过误差估计使声源特性求解结果更加稳定，从而能够有效对发动机声源识别误差进行控制。

5　声源特性识别结果验证

本小节对传统四负载法和本文提出的方法获取的声源特性结果进行验证。验证方法为选取一个带内插管的膨胀腔进行发动机台架试验，测量得到尾管辐射噪声的声压级。然后对带内插管的膨胀腔进行三维声流耦合仿真，将获得的声源特性结果施加到声学仿真模型的入口边界上，再计算尾管远场辐射声压级。最后将试验结果与仿真结果进行对比即可验证两种计算方式得到的发动机声源特性结果的准确性。

内插管膨胀腔的几何尺寸以及试验测试中的实物照片如图11所示。

图11　内插管膨胀腔的几何尺寸及实物照片Fig.11 The physical dimension and photograph of the expansion chamber with insert tube

采用CFD方法[19]对内插管膨胀腔内部的流场进行计算，计算结果如图12所示。再将流场计算结果通过积分插值运算映射到声场网格上，从而使得声场的计算能够充分考虑非均一流场场量的影响。从图12可以看出，内插管膨胀腔内部呈现复杂的流场以及温度场分布，必定会对管内的声传播产生影响。因而将流场信息耦合到声场计算中，可以大大减小仿真误差。在完成流场信息插值计算以后，对声场仿真模型施加激励，然后进行耦合场情况下的声传播计算。

图12　内插管膨胀腔内部流场仿真结果Fig.12 The internal flow field simulation results of the expansion chamber with insert tube

要将声源特性结果施加到声场仿真模型的入口边界上，先要将声源阻抗换算成声源导纳，将声源声压换算成加速度激励。换算方法如式(25)和式(26)所示。式中YE是入口边界处的声源导纳，ɑE是入口处的加速度激励。

(25)

(26)

内插管膨胀腔最终的声场仿真模型如图13所示。

将仿真模型中远场响应点在各阶次处的辐射声压值提取出来，与试验测试结果进行对比如图14所示。

图13　声源特性参数验证的声学仿真模型Fig.13 The acoustic simulation model for the verification of engine source characteristics results

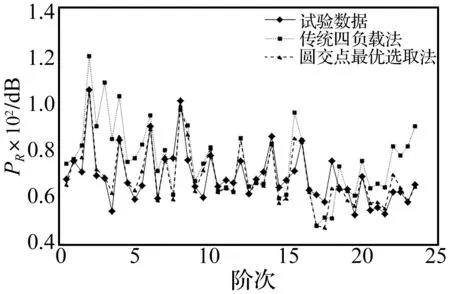
图14　内插管膨胀腔远场辐射噪声仿真结果与试验对比Fig.14 The comparison of the radiated sound pressure level between simulation and experiment for the expansion chamber with insert tube

从图14中可以看出，在各阶次处传统四负载法的远场辐射噪声仿真结果与试验结果偏差较大，尤其在8阶以下的结果明显高于试验测试的结果。而本文中提出的基于误差估计的圆交点最优选取法的远场辐射噪声仿真结果与试验结果吻合良好，充分说明本文中提出发动机声源特性求解方法可以有效地减小识别误差，从而获取更为准确的发动机声源特性参数。

6　结　论

本文从误差估计的角度出发，建立了间接法声源特性识别的声源声压离散度估计和声源阻抗值偏差估计，将识别模型中的超定非线性方程组中的方程式进行两两组合，通过解析几何的方法直接求解方程组，然后再利用声源阻抗值偏差估计选取最优解。本文提出的方法克服了传统四负载法通过替代消除方程组中的二次项，将超定非线性方程组转化成线性方程组所带来的对输入误差敏感、容易产生极大误差的缺点。最后通过仿真和试验相结合的方法验证了本文中提出的方法的有效性和准确性。本文研究主要得到以下结论：

(1) 建立的间接法声源特性识别的误差估计方法可对识别结果的误差大小进行估计，为声源特性参数求解结果的选取提供了判别依据。

(2) 提出的基于误差估计的圆交点最优选取法可以使声源特性求解结果更加稳定，从而能够有效控制输入误差对声源特性识别结果的影响。

(3) 采用仿真和试验相结合的方法可以对源特性识别结果进行验证。验证结果对比表明本文提出的方法克服了传统四负载法的缺陷，提高了发动机声源特性识别精度，为源特性参数的准确识别提供了新方法。

[1] DOKUMACI E. Prediction of source characteristics of engine exhaust manifolds[J]. Journal of Sound and Vibration, 2005, 280(3/4/5): 925-942.

[2] 刘海涛，郑四发，康钟绪，等．基于四负载方法的汽车发动机排气源特性研究[J]．振动工程学报，2011，24(5)：573-577.

LIU Haitao, ZHENG Sifa, KANG Zhongxu, et al. Acoustical source characteristics of vehicle exhuast system based on the four-load method[J]. Journal of Vibration Engineering, 2011, 24(5):573-577.

[3] BODEN H. The multiple load method for measuring the source characteristics of time-variant sources[J]. Journal of Sound and Vibration, 1991, 148(3): 437-453.

[4] RAMMAL H, BODEN H. Modified multi-load method for nonlinear source characterisation[J]. Journal of Sound and Vibration, 2007, 299(4/5): 1094-1113.

[5] MACIAN V, TORREGROSA A J, BROATCH A. A view on the internal consistency of linear source identification for I.C. engine exhaust noise prediction[J]. Mathematical and Computer Modelling, 2013, 57(7/8): 1867-1875.

[6] GALAITISIS G A, BENDER K E. Measurement of the acoustic impedance of an internal combustion engine[J]. Journal of the Acoustical Society of America, 1975, 58(1): S8.

[7] PARSAD G M, CROCKER J M. Acoustical source characteriztion studies on a multi-cylinder engine exhaust system[J]. Journal of Sound and Vibration, 1983, 90(4): 490-497.

[8] ROSS F D, CROCKER J M. Measurement of the acoustic internal source impedance of an internal combustion engine[J]. Journal of the Acoutical Society of America,1983,74(1): 18-27.

[9] DOIGE G A, ALVES S H. Experimental characterization of noise source for duct acoustics[J]. Journal of Vibration and Acoustics, 1989, 111(1): 108-114.

[10] ALVES H S. Characterization of noise sources in ducts[D].Calgary, Canada: The University of Calgary, 1986.

[11] PRASAD G M. A four load method for evaluation of acoustic source impedance in a duct[J]. Journal of Sound and Vibration, 1987, 114(2): 347-356.

[12] BODEN H. On multi-load methods for determination of the source data of acoustic one-port sources[J]. Journal of Sound and Vibration, 1995, 180(5): 725-743.

[13] JANG H S, IH G J. Refined multiload method for measuring acoustical source characteristics of an intake or exhaust system[J]. Journal of the Acoustical Society of America, 2000, 107(6): 3217-3225.

[14] SRIDHARA S B, CROCKER J M. Error analysis for the four-load method used to measure the source impedance inducts[J]. The Journal of the Acoustical Society of America,1992,92(5):2924-2931.

[15] MUNJAL L M. Acoustic of ducts and mufflers[M]. 2nd ed. New York: John Wiley, 2014.

[16] RIENSTRA W S. A small strouhal number analysis for acoustic wave-jet flow-pipe interaction[J]. Journal of Sound and Vibration, 1983, 86(4): 539-556.

[17] TIIKOJA H, LAVRENTJEV J, RAMMAL H. Experimental investigations of sound reflection from hot and subsonic flow duct termination[J]. Journal of Sound and Vibration, 2014, 333(3): 788-800.

[18] MUNT R M. Acoustic transmission properties of a jetpipe with subsonic jet flow: I. the cold jet reflection coefficient[J]. Journal of Sound and Vibration, 1990, 142(3): 413-436.

[19] 徐航手，季振林，康钟绪. 抗性消声器传递损失预测的三维时域计算方法[J]. 振动与冲击，2010, 29(4): 107-110.

XU Hangshou, JI Zhenlin, KANG Zhongxu.Three-dimensional time-domain computational approach for predicting transmission loss of reactive silencers [J]. Journal of Vibration and Shock, 2010, 29(4): 107-110.

On the solving method of the indirect source characteristics identification model for an engine exhaust system based on error estimation

LIU Haitao1,2, LIAN Xiaomin2, LIU Linya1

(1. School of Mechatronics & Vehicle Engineering, East China Jiaotong University, Nanchang 330013, China；2. State Key Laboratory of Automotive Safety and Energy, Tsinghua University, Beijing 100084, China)

Linear time-invariant hypothetical model solved in the frequency domain for the determination of engine source characteristics plays a practical role in the engine exhaust system design. However, the error of existing methods for solving the model is large, the results are sensitive to input error, and the identification and solving processes are complicated. In order to improve the accuracy of engine source characteristics identification results, an error estimation method was established for the indirect identification model, namely source strength level dispersion estimation and source impedance deviation estimation. The equation from the over-determined nonlinear equations in the identification model was pairwise combined, which were directly solved by an analytic geometry method. Multiple source characteristic parameter solutions were obtained. And then the optimal solution was selected by the source impedance deviation estimation. According to analysis and calculation, the error value of the source characteristic parameters acquired by the method above, is significantly lower than the traditional four-load method. Finally, the three-dimensional coupled simulation of acoustic and flow method was used to verify the results of source characteristic identification. The sound pressure level of far-field response point predicted by simulations agrees well with experimental results, which indicates that the optimal source characteristic parameters selection method based on error estimation can achieve more accurate source identification results, and can efficiently reduce the identification error and complexity.

engine; source strength; source impedance; error estimation; coupled simulation of acoustic and flow

国家自然科学基金(51268014)；华东交通大学科研基础经费(26541022)

2015-05-26修改稿收到日期：2015-08-01

刘海涛 男，博士，讲师，1986年1月生

U464.134.4

A

10.13465/j.cnki.jvs.2016.16.016