稳态雷暴冲击风风速剖面模型研究

邹　鑫， 汪之松,2， 李正良,2

(1.重庆大学 土木工程学院，重庆　400045； 2.重庆大学 山地城镇建设与新技术教育部重点实验室，重庆　400045)



稳态雷暴冲击风风速剖面模型研究

邹鑫1， 汪之松1,2， 李正良1,2

(1.重庆大学 土木工程学院，重庆400045； 2.重庆大学 山地城镇建设与新技术教育部重点实验室，重庆400045)

雷暴冲击风是非台风地区形成极值风荷载的主要原因。采用静止型冲击射流装置和大涡模拟分别对雷暴冲击风风场进行了物理试验和数值模拟，考察了径向风速和竖向风速的分布特征。将大涡模拟结果和试验结果与现有实测数据和理论模型进行了对比，验证了试验和数值模拟结果的可靠性。针对现有的径向风速模型并不适用于所有径向位置处径向风速的问题，结合物理实验和大涡模拟的结果，提出了沿径向变化的径向风速剖面模型。同时，根据风场竖向风速的特点将其沿径向位置分为三个区域，给出了三个区域竖向风速剖面模型。

雷暴冲击风;冲击射流模型;大涡模拟;风场特性

目前建筑结构抗风设计均是按照大气边界层风场进行的。然而，相关统计资料显示，雷暴冲击风才是多数非台风地区极值风速产生的主要原因[1]。在我国，因为雷暴冲击风而造成结构破坏的案例也时有发生，如2005年6月14日，500 kV任上线发生的雷暴冲击风致输电塔倒塔事故[2]等。雷暴冲击风风场与大气边界层风场截然不同，有必要展开对雷暴冲击风风场特性的研究。

自从Fujita[3]首次提出雷暴冲击风的危害以来，国外学者对雷暴冲击风风场进行了诸多研究。Oseguera等[4]基于风场轴对称性，提出了柱坐标下的风场模型(OB模型)；Vicroy[5]通过优化形函数，对OB模型进行改进，提出了OBV模型。Holmes等[6]通过矢量叠加法，提出了运动雷暴冲击风径向和竖向风速模型，并与1983 AFB 雷暴冲击风实测结果进行对比，两者吻合较好。Chay等[7]对雷暴冲击风在数值模拟基础上，提出了考虑时变效应的雷暴冲击风风场模型。Wood[8]拟合冲击射流实验结果，提出了稳态雷暴冲击风水平风速竖向风剖面模型，该模型与1.5D～2D径向位置处测试结果吻合较好，与1D位置处试验结果相差较大。Sengupta等[9]进行冲击射流物理实验，使用热线和PIV两套风速测试设备，考察了各径向位置平地风场，并与实测数据和经验公式进行了对比。Vermerie 等[10]运用冷源模型对雷暴冲击风进行了数值模拟。Zhang等[11]对比了冲击射流模型和冷源模型模拟的雷暴冲击风风场，给出了两种模型的优缺点。

Orf等[12]采用三维云模型对雷暴冲击风进行了数值模拟，并比较了三维云模型，冷源模型和冲击射流模型之间的差别。

国内方面，李宏海等[13]采用二维模型进行数值模拟，得到与各经验模型相吻合的雷暴冲击风风场。陈勇[14]采用RNGk-ε模型进行冲击射流稳态数值模拟，提出了水平和竖向风速经验模型。陈勇[15]通过分析运动冲击射流物理试验结果，提出适用于不同冲击风参数的现象模型。瞿伟廉[16]采用非定常雷诺平均方法对1∶2 000缩尺模型进行仿真，得到了与实测数据相吻合的风剖面。汤卓等[17]采用大涡模拟的方法模拟了雷暴冲击风风场，考察了地面风压分布情况。李锦华等[18]通过考虑自回归AR模型时变性，建立了非平稳随机过程TAR时变模型，并用来进行雷暴冲击风非平稳脉动风速的模拟。

目前雷暴冲击风物理模型大致有环状涡旋模型，冲击射流模型，冷源模型和三维云模型等。冲击射流模型模拟的平均风速剖面与实测数据吻合较好[11]，且易于在实验室实现而成为研究雷暴冲击风风场的首选。本文采用静止型冲击射流模型，分别通过物理实验和数值模拟的方式研究了稳态雷暴冲击风风场，提出了竖向风速和径向风速模型，为雷暴冲击风抗风设计提供了一定依据。

1　冲击射流试验概况

冲击射流试验装置上如图1所示。冲击射流装置射流直径D=600 mm，射流口到底板距离H=1 200 mm，H/D=2。射流速度vjet=12 m/s。几何缩尺比1∶1 000。采用热线风速仪进行雷暴冲击风风场测试。热线采样频率5 000 Hz，采样时长20 s，每个径向位置沿高度10 mm～180 mm，逐次测量15个点。

图1　冲击射流试验装置Fig.1 Impinging jet instrument

2　数值模拟概况

为了与缩尺试验结果对比，采用大涡模拟(LES)进行冲击射流风场的数值模拟。CFD软件采用Ansys Fluent 14.0。射流速度为vjet，速度入口湍流度为1%，射流直径为D，喷口到底板的距离为H=2D，计算域总高3D，长12D。数值模拟计算域示意见图2。图3给出了计算流域网格划分示意。大涡模拟亚格子尺度模型采用Smagorinsky-Lilly模型，模型常数Cs=0.1。压力和速度场耦合采用SIMPLEC算法，流体空间离散采用二阶迎风格式进行。

数值模型近壁面网格均满足无量纲距离y+≤1。由于计算域很大，近壁面加密之后的足尺模型超过1 000万网格，数值计算代价很大。考虑采用和试验相同缩尺比1∶1 000的缩尺模型进行数值模拟。图4给出了采用足尺模型和缩尺模型进行大涡模拟得到的r=1.5D位置处径向平均风速剖面的比较，可以看到两种模型风场几乎完全一致。综合考虑计算精度和计算花费之后，采用1∶1 000缩尺模型进行雷暴冲击风风场的大涡模拟。为了验证数值模型的网格依赖性，选取了5种不同网格数量模型分别进行雷暴冲击风场的数值模拟。图5给出了在r=1D处风场结果进行对比，可以看出不同网格数量模型数值模拟结果基本吻合，数值模型已经满足了网格无关的要求。后续研究所采用的缩尺模型网格数为280万，计算时间步长为0.001 s。

图2　计算域示意图Fig.2 Calculation domain illustration

图3　计算域网格截图Fig.3 Grid meshing of calculation domain

图4　足尺模型与缩尺模型风场比较(r=1.5D)Fig.4 Comparison of full scale model and the 1∶1 000 scale model (r=1.5D)

图5　缩尺模型网格依赖性研究(r=1D)Fig.5 Study of mesh independence(r=1D)

3　结果与讨论

3.1径向风速分布

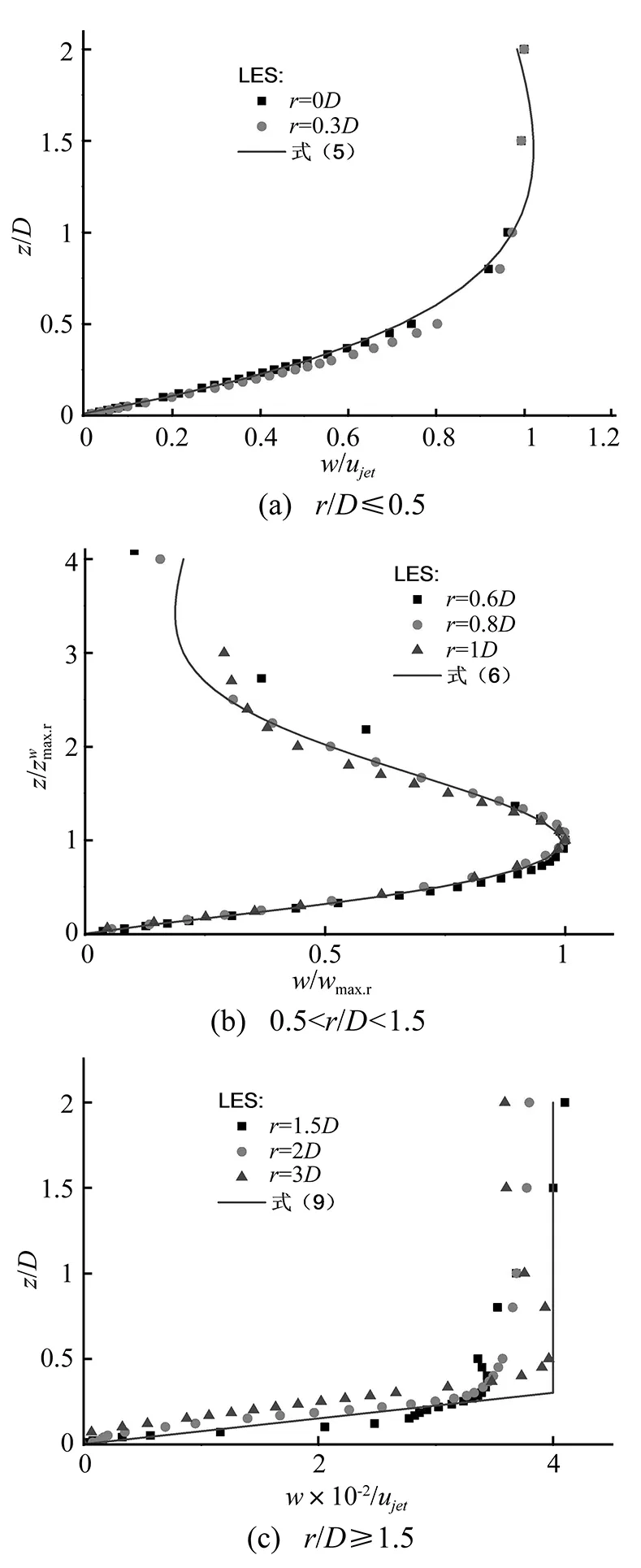
试验测试了r=0.6D～3D范围内各径向位置处水平风速。图6给出了热线测试结果。在靠近喷筒边缘的0.6D和0.8D位置，径向风速还没有发展充分。r=0.6D处，径向风速沿高度几乎不变，在较高位置处有略微增大。而r=0.8D处，径向风速剖面开始趋近于充分发展的1D位置处剖面。从1D开始，充分发展的径向风速剖面已经形成，径向风速沿高度均先增大，然后减小，最大径向风速出现在靠近底部的位置。在r=1D～3D处，随着径向位置的远离，径向风速逐渐减小。各径向位置处径向风速最大值umax.r从1D位置处最大1.05vjet，逐渐减小到3D位置处0.54vjet。同时，从r=1D至r=3D，umax.r出现的高度有逐渐增高的趋势。

图6　不同径向位置径向风速剖面Fig.6 Radial-velocity profiles for different r/D

图7　不同径向位置径向风速剖面比较Fig.7 Comparison of radial-velocity profiles at various locations

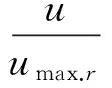
(1)

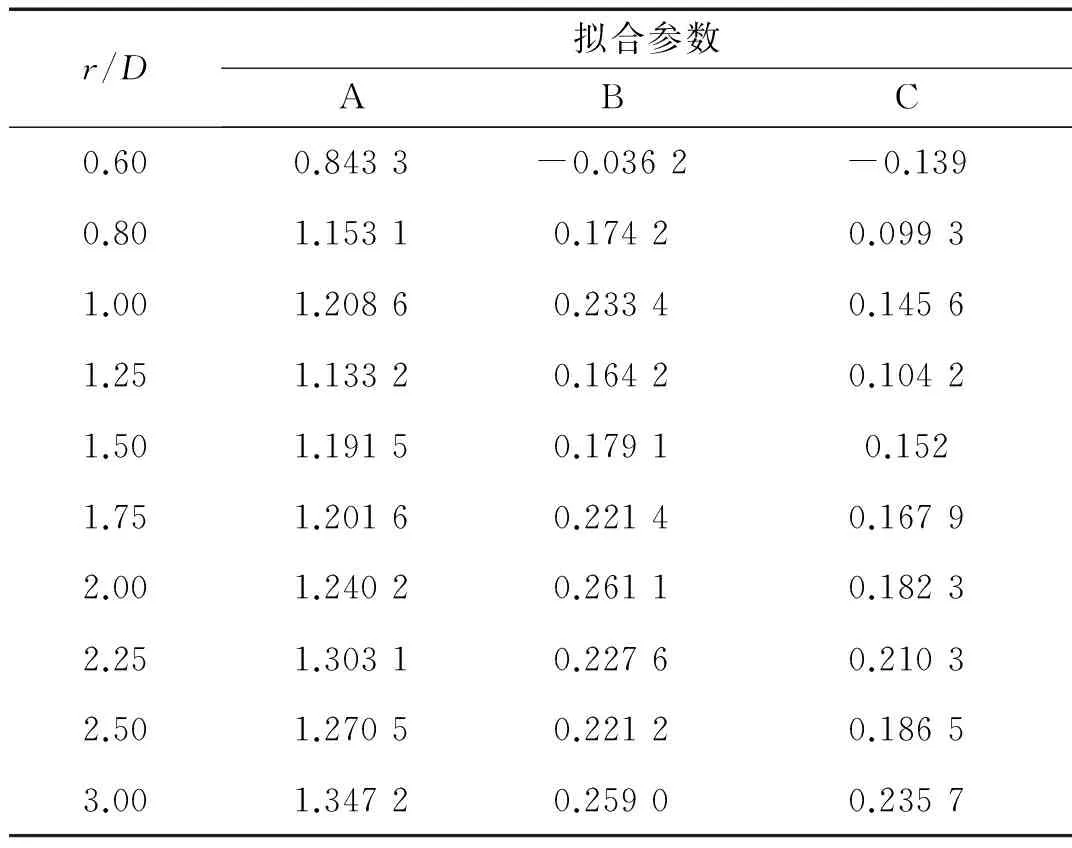
式中:erf为误差函数。A、B、C为待定拟合参数。拟合结果详见表1。

图8给出了各径向位置拟合剖面与试验结果的对比。由图可见，在各个径向位置处，两者均吻合较好。

将参数A、B、C对于r/D进行二次拟合，得到拟合参数计算公式如下：

A=0.115 8(r/D)3-0.692 4(r/D)2+

图8　各径向位置径向风速剖面拟合Fig.8 Fitting of radial velocity profiles at different radial locations

图9　参数A、B、C拟合Fig.9 Fitting of parameter A,B and C

(3)

(4)

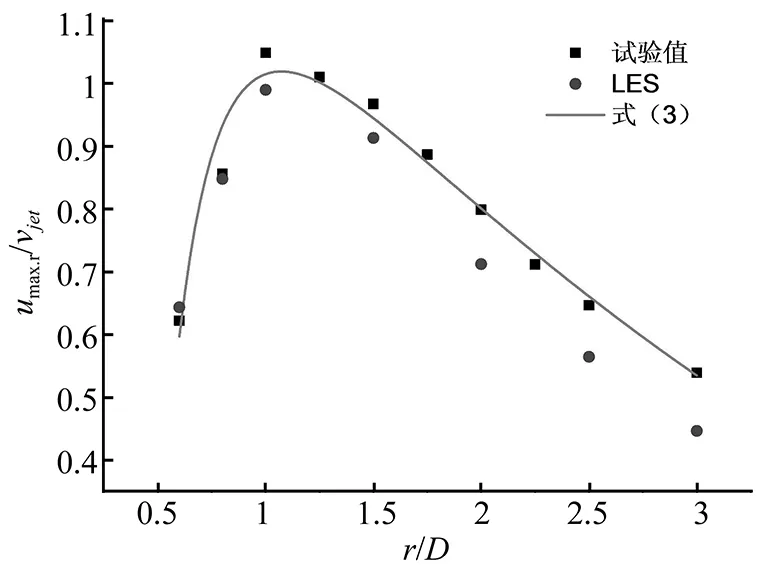
图10　最大径向风速随径向位置的变化Fig.10 Maximum radial-velocity at different r/D

图11　各径向位置Fig.

3.2竖向风速分布

雷暴冲击风是由于强烈的下沉气流冲击地面后向四周发散产生的。因此，研究雷暴冲击风风场除了水平向的径向速度之外，还因考虑整体风场的竖向速度分布。试验测试了射流口正下方距离底板0.25H，0.5H和0.75H三个高度处竖向风速。定义竖向风速向下为正。图12给出了热线测试结果与大涡模拟结果的对比。竖向风速在接近射流口的0.75H和0.5H高度处，数值上与vjet相近且沿径向分布较为均匀。在0.25H高度处，底板对竖向速度分布影响明显，竖向风速在射流中心位置最小，在射流口边缘位置处较大。竖向风速的大涡模拟结果与试验结果吻合较好，证明数值模拟得到的雷暴冲击风风场是可靠的。

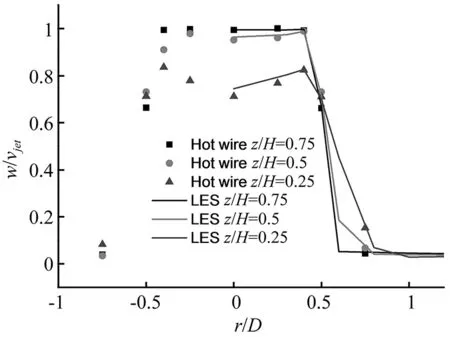
图12　射流口正下方竖向速度分布Fig.12 Vertical velocity distribution just below the impinging jet

采用大涡模拟的结果来研究雷暴冲击风风场竖向风速分布特征。图13为不同径向位置处竖向风速沿高度的分布。由图可见，在射流口正下方(r/D≤0.5)，竖向风速沿高度一直增大，直至达到射流速度vjet。在靠近射流喷筒附近(0.5

图13　不同径向位置竖向速度分布Fig.13 Vertical velocity distribution at different radial locations

结合上述分析，对雷暴冲击风风场竖向风速的描述沿径向位置分为三个区域。

当r/D≤0.5时：

(5)

当0.5

(6)

式中：wmax.r为r径向位置竖向风速最大值，采用下式计算：

(7)

(8)

当r/D≥1.5时：

(9)

图14给出了拟合式(5)(6)(9)与大涡模拟结果对比。可以发现，给出的竖向风速剖面模型能够较好的描述雷暴冲击风竖向风场。

图14　竖向风速剖面拟合Fig.14 Fitting of the vertical velocity profiles

4　结　论

本文采用静止型冲击射流模型模拟稳态雷暴冲击风风场，通过分析物理试验和大涡模拟结果，得到如下结论：

(1) 稳态雷暴冲击风风场最大径向风速出现在r=1D位置处，最大径向速度出现在近地面附近，数值约为1～1.05vjet。

(2) 现有的径向风速模型并不适用于所有径向位置处径向风速，本文结合物理实验和大涡模拟的结果，提出了沿径向变化的径向风速剖面的拟合公式。

(3) 对于雷暴冲击风风场，竖向风速不能忽略。大涡模拟的结果显示，竖向风速沿径向位置分了三个区域，本文结合其分布特征给出了适用于三个区域竖向风速剖面模型。

(4) 对稳态雷暴冲击风风场研究结果能够为稳态雷暴冲击风抗风设计提供依据，并为后续关于雷暴冲击风非稳态特征的研究提供一定的参考。

[1] Letchford C W, Mans C, Chay M T, Thunderstorms—their importance in Wind Engineering, a case for the next generation wind tunnel, JAWE J. Wind Eng,2001,89:31-43.

[2] 谢强，张勇，李杰．华东电网500 kV 任上5237 线飑线风致倒塔事故调查分析[J]．电网技术，2006，30(10)：59-63．

XIE Qiang，ZHANG Yong，LI Jie．Investigation on tower collapses of 500 kV RenShang 5237 transmission line caused by downburst[J]．Power System Technology，2006，30(10)：59-63.

[3] Fujita T T. The downburst[R]. Report of Projects NIMROD and JAWS, University of Chicago: T.T. Fujita, 1985.

[4] Oseguera R M, Bowles R L. A simple analytic 3-dimensional downburst model based on boundary layer stagnation inflow [R]. NASA Technical Memorandum 100632, 1988.

[5] Vicroy D D. A simple, analytical, asymmetric microburst model for downdraft estimation [R]. NASA Technical Memorandum 104053, 1991.

[6] Holmes J D, Oliver S E. An empirical model of a downburst [J].Engineering Structures, 2000, 22:1167-1172.

[7] Chay M T, Albermani F, Wilson R. Numerical and analytical simulation of downburst wind loads [J]. Engineering Structures, 2006, 28(2): 240-254.

[8] Wood G S, Kwok K C S, Motteram N A, et al. Physical and numerical modeling of thunderstorm downbursts [J]. Wind Eng.Ind.Arodyn,2001(89):535-552.

[9] Sengupta A,Sarkar P P. Experimental measurement and numerical simulation of an impinging jet with application to thunderstorm microburst winds [J]. Journal of wind Engineering and Industrial Aerodynamics,2008,96(3):345-365.

[10] Vermeire B C, Orf L G, Savory E. Improved modelling of downburst outflows for wind engineering applications using a cooling source approach [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2011, 99(8):801-814.

[11] Zhang Yan, Hu Hui ,Sarkar P P. Modeling of microburst outflows using impinging jet and cooling source approaches and their comparison [J].Engineering Structures,2013,56: 779-793.

[12] Orf L, Kantor E, Savory E. Simulation of a downburst-producing thunderstorm using a very high-resolution three-dimensional cloud model [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2012, 104-106:547-557.

[13] 李宏海，欧进萍. 雷暴冲击风作用下建筑物表面风压分布模拟[C]//第19届全国结构工程学术会议论文集(第Ⅲ册).工程力学，2010:76-80.

[14] 陈勇，彭志伟，楼文娟,等. 冲击风稳态流场CFD模拟及三维风速经验模型研究[J]. 计算力学学报，2010,27(3)：428-434.

CHEN Yong, PENG Zhi-wei, LOU Wen-juan, et al. CFD simulations of steady downburst and 3D wind velocity empiricalmodels [J]. Chinese Journal of Computational Mechanics, 2010, 27(3):428-434.

[15] 陈勇，柳国光，徐挺，等. 运动雷暴冲击风水平风速时程分析及现象模型[J]. 同济大学学报:自然科学版，2012,40(1):22-26.

CHEN Yong, LIU Guo-guang, XU Ting, et al. Time histories of horizontal wind velocity of moving thunderstorms and phenomenological model [J]. Journal of Tongji University:Natural Science, 2012, 40(1):22-26.

[16] 瞿伟廉, 吉柏锋, 李健群,等. 下击暴流风的数值仿真研究[J]. 地震工程与工程振动, 2008, 28(5): 133-139.

QU Wei-lian, JI Bai-feng, LI Jian-qun, et al. The study on numerical simulation of downburst wind [J]. Journal of earthquake engineering and engineering vibration, 2008, 28(5):133-139.

[17] 汤卓，吕令毅. 雷暴冲击风作用下地面风压分布特征[J]. 东南大学学报:自然科学版, 2011, 41(6): 1273-1276.

TANG Zhuo, LÜ Ling-yi. Wind pressure distribution on ground under impingement of downbursts[J]．Journal of Southeast University:Natural Science Edition，2011，41(6): 1273-1276．

[18] 李锦华,吴春鹏,陈水生.下击暴流非平稳脉动风速数值模拟[J].振动与冲击,2014,33(14):54-60.

LI Jin-hua, WU Chun-peng, CHEN Shui-sheng. Simulation of non-stationary fluctuating wind velocity in downburst [J].Journal of Vibration and Shock, 2014, 33(14):54-60.

Wind velocity profile model of steady thunderstorm downburst

ZOU Xin1, WANG Zhisong1,2, LI Zhengliang1,2

(1.College of Civil Engineering, Chongqing University, Chongqing 400045, China; 2. Key Laboratory of New Technology for Construction of Cities in Mountain Area, Ministry of Education Chongqing University, Chongqing 400045, China)

Thunderstorm downburst is the main cause for formation of extreme wind loads in non-typhoon areas. Here, both the static impinging jet device and the large eddy simulation(LES) were used to do the physical experiment and numerical simulation for thunderstorm downburst. The distribution features of radial and vertical wind velocities were investigated. Aiming at that the existing radial wind velocity profile model was not applicable to the radial wind velocity distributions at all radial locations, combining the results of the experiment and LES, a new radial wind velocity profile model being suitable to all radial locations was proposed. Meanwhile, the wind flied was divided into three parts according to the characteristics of vertical wind velocity, the vertical wind velocity profile models were presented for all the three parts.

thunderstorm downburst; impinging jet model; large eddy simulation(LES); wind-tunnel test; wind-field characteristics

国家自然科学基金项目(51208537);中央高校基本科研业务费(CDJZR 12 20 00 16)

2015-02-02修改稿收到日期：2015-07-18

邹鑫 男，博士生，1986年生

汪之松 男，博士，副教授，1980年生

TU311

A

10.13465/j.cnki.jvs.2016.15.012