基于分数阶导数的沥青胶浆动态力学特性

李锐铎， 乐金朝， 李瑞霞， 姚立阳

(1.郑州大学 水利与环境学院，郑州　450002； 2.河南城建学院 交通运输工程学院，河南 平顶山　467036)



基于分数阶导数的沥青胶浆动态力学特性

李锐铎1,2， 乐金朝1， 李瑞霞1， 姚立阳2

(1.郑州大学 水利与环境学院，郑州450002； 2.河南城建学院 交通运输工程学院，河南 平顶山467036)

通过对粉胶比为0.62、0.82、1.02、1.22和1.42的沥青胶浆在20℃、30℃、40℃和50℃条件下进行动态频率扫描试验，研究了不同粉胶比及试验温度条件下沥青胶浆复模量、抗车辙因子和相位角的变化规律。基于分数阶导数理论，建立了Nutting蠕变方程与经典分数阶导数Abel黏壶蠕变模型之间的关系，从而明确了Nutting蠕变方程各参数的物理意义。对分数阶Riemann-Liouville算子黏弹性蠕变本构模型的动态力学响应进行分析，提出了利用沥青胶浆动态频率扫描试验结果确定蠕变本构模型中参数A值和γ值的新方法。

沥青胶浆;粉胶比;动态剪切流变试验;分数阶导数;Nutting蠕变方程;变形因子;黏弹因子

按照胶浆理论，沥青胶浆是构成沥青混合料的微分散系，主要起填充细集料空隙和黏结作用[1]，其组成结构决定了沥青混合料的高低温性能。沥青胶浆是典型的黏弹性材料，常用经典的元件模型描述其力学性能[2]。元件模型主要由弹簧元件和黏壶元件构成，不同的元件数量及组合形式构成了 Maxwell、Kelvin、Kelvin-Voigt、广义Maxwell、广义Kelvin、广义Kelvin-Voigt、Burgers等模型。近几十年来，国外许多学者[3-6]以及国内的刘丽等[7-10]先后采用传统的力学理论及评价指标对沥青胶浆的性能进行了深入研究。但传统的力学模型存在参数多、参数确定不便和不能精确描述材料的力学特性等缺点。

近年来，分数阶导数模型因为能够克服经典整数阶微分模型与试验结果吻合不好的缺点而被广泛应用于各个工程领域[11-13]。Celauro等[14-15]依据幂函数经验方程构建了以分数阶Riemann-Liouville算子描述黏弹性材料黏弹性应变的蠕变本构模型，并对纯沥青的力学特性进行了研究。李锐铎等[16]提出了改进的分数阶导数经验蠕变模型并利用该模型来描述沥青胶砂的蠕变特性。

鉴于沥青胶浆组成的微分散系对沥青混合料的性质起着重要影响，本文结合分数阶导数模型优势建立了Nutting蠕变方程[17]与经典分数阶导数Abel黏壶蠕变模型之间的关系。以不同粉胶比的沥青胶浆为研究对象，研究不同温度条件下的沥青胶浆动态力学特性，探讨Nutting蠕变方程各参数表征的物理意义，并提出利用动态剪切流变试验结果进行一元线性回归分析来确定蠕变方程的参数，为进一步深入研究沥青胶浆在不同温度条件下的动态流变性能提供借鉴。

1　分数阶导数黏弹性本构模型

黏弹性高聚物材料的蠕变服从Nutting公式[17]：

lgε(t)=lgA+γlgt+lgσ,0<γ<1

(1)

其蠕变柔量

J(t)=Atγ,0<γ<1

(2)

式中：A、γ为反映材料性能的材料参数，可通过试验确定。

Celauro等[18]依据幂函数经验方程构建了以分数阶Riemann-Liouville算子描述黏弹性材料黏弹性应变的蠕变本构模型如式(3)所示

(3)

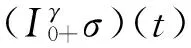
Koeller等[19]以Abel黏壶元件模型构建的黏弹性材料的蠕变柔量为

0≤γ≤1

(4)

式中：Γ(1+γ)为1+γ的gamma函数；φ(t)为蠕变柔量单位阶跃函数，即

当γ=1时，该元件为Newton黏壶，代表理想流体，γ=0时，该元件变为弹簧元件，代表理想固体。

2　分数阶导数黏弹性本构模型动态力学特性

在交变应力荷载作用下，基于分数阶导数的黏弹性材料的本构方程[15]为

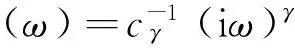
(5)

式中：G*(ω)=G1(ω)+iG2(ω)；G*(iω)为动态剪切模量，G1(ω)为存储模量，G2(ω)为损耗模量。

将cγ=AγΓ(γ)代入式(5)并取绝对值可得

(6)

3　试验材料及试验条件确定

3.1试验材料

沥青为重交70号石油沥青，基本技术性质测试结果如表1所示。填料为石灰石矿粉，对矿粉试样进行X衍射分析(如图1所示)，主要包含了CaC03、CaMg(C03)2和SiO2衍射峰。其密度为2.814 g/cm3，亲水系数为0.86。参照实际工程沥青混合料配合比中粉胶比，使用高速剪切乳化机制备粉胶比分别为0.62、0.82、1.02、1.22和1.42的沥青胶浆。

表1　基质沥青基本技术性质

图1　矿粉XRD衍射图谱Fig.1 XRD diffraction pattern of mineral powder

3.2线黏弹性范围确定

剪切流变仪测试原理是基于流变学线黏弹性假设的基础上，对基质沥青及粉胶比为1.42的沥青胶浆进行应变扫描试验，结果如图2所示。可以看出：随着粉胶比的增大，线黏弹性应变范围逐渐降低，同一粉胶比条件下，温度越低，线黏弹性范围也越小。因此，为保证所有试样均能处于线黏弹性范围内，并考虑试验数据分析方便，最终确定在进行频率扫描时的应变幅值为0.1%。

4　试验结果及分析

4.1沥青胶浆动态频率扫描试验结果及分析

沥青胶浆频率扫描试验结果如图3所示。可以看出：① 在双对数坐标中，同一温度条件下，任一粉胶比沥青胶浆的复数剪切模量随着角频率的增加而线性增加；② 在不同温度条件下，同一粉胶比沥青胶浆的复数剪切模量均随着温度的增加而减小，说明其抗变形能力随着温度的升高而降低。而对于不同粉胶比，复数剪切模量随着粉胶比的增大而增大。说明矿粉含量的增大提高了沥青胶浆的抗变形能力。

图2　沥青胶浆应变扫描曲线图Fig.2 Asphalt mortar dynamic shear strain scan

沥青胶浆的抗车辙因子(G*(ω)/sinδ)[20]与粉胶比和温度关系如图4所示。可以看出：① 除40℃条件下粉胶比为1.42的沥青胶浆的抗车辙因子比粉胶比为1.22的沥青胶浆略低外，其它不同温度条件下，随着粉胶比的增大，沥青胶浆的抗车辙因子均有所增大。说明从沥青混合料的高温稳定性考虑，宜选用较大的粉胶比，但并非粉胶比越大越好，过大的矿粉含量不但会增大沥青用量，增加工程造价，同时矿粉也不宜均匀分散在沥青混合料中，影响沥青混合料整体结构的高温稳定性；② 当粉胶比增大，随着温度的降低，抗车辙因子急剧增大。说明温度对沥青胶浆的抗车辙因子有着重要影响。

图3　沥青胶浆动态频率扫描曲线Fig.3 Dynamic frequency scanning curve of asphalt mortar

图4　不同粉胶比不同温度沥青胶浆抗车辙因子Fig.4 The rutting factor of asphalt mortar at at different temperature and ratio

动态频率扫描试验得到的沥青胶浆的相位角(振荡角频率为10 rad·s-1)如图5所示。可以看出：① 对同一粉胶比，相位角随着温度的升高逐渐增大，说明沥青胶浆的黏性特性越来越强；② 随着粉胶比的增大，各温度条件下的相位角均逐渐降低，说明矿粉含量的增加增强了沥青胶浆的弹性固体特性。

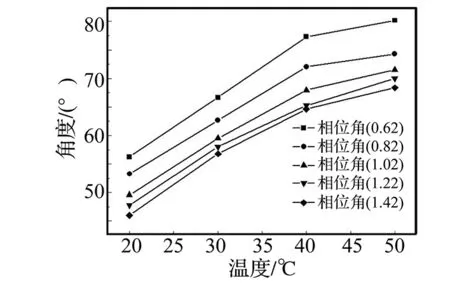
图5　不同粉胶比不同温度沥青胶浆相位角Fig.5 The phase angle of asphalt mortar at different temperature and ratio

4.2基于分数阶导数沥青胶浆动态力学特性分析

基于分数阶导数的黏弹性材料的本构方程可以表示为式(6)，其中A和γ均为材料参数，对特定材料其为常数。为了确定材料参数A和γ，可将式(6)改写为，

y=a+bx

(7)

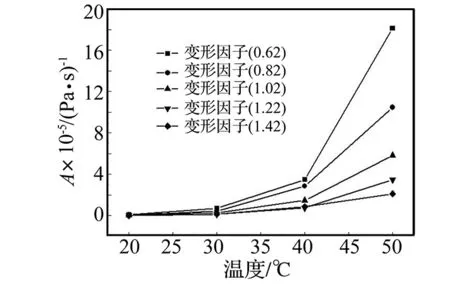
图6　不同粉胶比和不同温度条件下拟合得到的A值Fig.6 The value of parameter A at different temperature and ratio

图7　不同粉胶比和不同温度条件下拟合得到的γ值Fig.7 The value of parameterγ at different temperature and ratio

由图6可知，A值随粉胶比的增大而减小；对任一粉胶比，随着温度的增高，A值逐渐增大，且矿粉含量越低，A值增加的幅度越大，说明A值对粉胶比和温度的变化均比较敏感。因此，同温度或同粉胶比条件下，A可以作为沥青胶浆的高温性能评价指标，称A为变形因子，A值越大，材料的高温稳定性越差。

由图7可知，同一温度条件下，粉胶比越大，说明沥青胶浆的弹性成分越大，而γ值越小；同一粉胶比条件下，随着温度的升高，沥青胶浆表现出来的黏性性能逐渐增加，越来越接近牛顿流体。因此，同温度或同粉胶比条件下，可以称γ为黏弹因子，γ值越大，沥青胶浆的黏性性能越强，而弹性越弱。

5　结　论

(1) 在双对数坐标中，对任一粉胶比的沥青胶浆同一温度条件下的复模量随着角频率的增加而线性增加；在不同温度条件下，沥青胶浆的复模量均随着温度的增加而减小；对不同粉胶比的沥青胶浆的复模量随着粉胶比的增大逐渐增大。

(2) 沥青胶浆的抗车辙因子随着粉胶比的增大逐渐增大，且随着温度的降低急剧增大，而相位角则逐渐降低，说明温度对沥青胶浆的抗变形能力有着重要的影响；同一粉胶比条件下，随着温度的升高，抗车辙因子逐渐降低，而相位角则逐渐增大。

(3) 基于分数阶导数理论，对Nutting蠕变方程和Abel黏壶蠕变方程进一步推导，建立了Nutting蠕变方程与经典分数阶导数Abel黏壶蠕变模型之间的关系，并进一步明确了Nutting蠕变方程的各参数的物理意义。提出A为变形因子，A值越大，材料的抗变形能力越差，而γ为黏弹因子，γ值越大，材料表现的黏性越强。对不同温度下的沥青胶浆的动态剪切流变试验结果进行了拟合分析，确定了Nutting蠕变方程中的变形因子和黏弹因子，提出一种确定Nutting蠕变方程参数的新方法。

[1] Puzinauskas V P. A study of mineral fillers in asphalt paving mixture[J]. Proceeding of the Association of Asphalt Paving Technologists,1961,30:439-440.

[2] 张肖宁. 沥青与沥青混合料的黏弹力学原理及应用[M]. 北京: 人民交通出版社,2006:31-42.

[3] Van der Poel C. A general system describing the visco elastic properties of bitumens and its relation to routine test data[J]. Journal Appl Chem., 1954, 4(5): 221-236.

[4] Anderson D A, Goetz W H. Mechanical behavior and reinforcement of mineral filler-asphalt mixtures[J]. Proc., Association of Asphalt Paving Technologists, 1973, 42: 37-66.

[5] Palade L I, Attané P, Camaro S. Linear viscoelastic behavior of asphalt and asphalt based mastic[J]. Rheol Acta, 2000, 39: 180-190.

[6] Kim Y R, Little D N. Linear viscoelastic analysis of asphalt mastic[J]. Journal of Materials in civil Engineering©ASCE/MARCH/APRIL, 2004, 16: 122-132.

[7] 刘丽. 沥青胶浆技术性能及评价方法研究[D]. 西安: 长安大学, 2004.

[8] 张争奇, 王永财. 沥青胶浆对沥青混合料高低温性能的影响[J]. 长安大学学报:自然科学版, 2006, 26(2): 1-5.

ZHANG Zheng-qi, WANG Yong-cai. Influence of asphalt mortar on hot mix asphalt performance at high and low temperature[J]. Journal of Chang’an University:Natural of Science, 2006, 26(2):1-5.

[9] 耿韩, 赵永利. 沥青胶浆路用性能的流变试验研究[J]. 公路工程, 2009, 34(1): 84-89.

GENG Han, ZHAO Yong-li. Pavement performance study of asphalt-mineral filler mastic by rheology test[J]. Highway Engineering,2009,34(1): 84-89.

[10] 樊亮, 魏建明, 张玉贞, 等. 矿粉对沥青胶浆的性质影响及作用机理[J]. 建筑材料学报, 2014, 17(6): 1096-1101.

FAN Liang, WEI Jian-ming, ZHANG Yu-zhen,et al. Acting mechanism and performance of asphalt mortars by mineral filler[J]. Journal of Building Materials,2014,17(6):1096-1101.

[11] Bagley R L. Power law and fractional calculus model of viscoelasticity[J]. AIAA Journal,1989,27(10):1412-1417.

[12] 陈文, 孙红广, 李西成. 力学与工程问题的分数阶导数建模[M]. 北京: 科学出版社, 2010: 7-10.

[13] 李军强, 刘宏昭,王忠民. 线性黏弹性本构方程及其动力学应用研究综述[J]. 振动与冲击,2005,24(2):116-122.

LI Jun-qiang, LIU Hong-zhao, WANG Zhong-min. Review on the linear the constitutive equation and its dynamics applicaions to visoelastic materials[J]. Journal of Vibration and Shock,2005,24(2):116-122.

[14] Celauro C, Fecarotti C, Pirrotta A, et al. Experimental validation of a fractional for creep/recovery testing of asphalt mixtures[J]. Construction and Building Materials, 2012, 36: 458-466.

[15] Fecarotti C, Celauro C, Pirrotta A. Linear viscoelastic behaviour of bitumen via fractional models[J]. Social and Behavioural Sciences, 2012(53): 450-461.

[16] 李锐铎, 乐金朝, 冯师蓉, 等. 沥青胶砂改进分数阶导数幂函数经验蠕变本构模型[J]. 建筑材料学报,2015,18(2):237-242.

LI Rui-duo, YUE Jin-chao, FENG Shi-rong, et al. Improved fractional order derivative empirical power function model for describing the creep of asphalt mortar[J]. Journal of Building Materials, 2015, 18(2): 237-242.

[17] 何平笙. 高聚物的力学性能[M]. 第2版. 合肥: 中国科学技术大学出版社, 2008: 104-105.

[18] Celauro C, Di Paolam M, Lo Presti D, et al. Modeling of the viscoelastic behavior of paving bitumen fractional derivatives[J]. Meccanica dei Materiali e delle Strutture, 2009, 1(2): 38-51．

[19] Koeller R C. Applications of fractional calculus to the theory of viscoelasticity[J]. Journal of Applied Mechanics, 1984, 51: 229-307.

[20] Anderson D A, Bahia H U, Christensen D W. Binder characterization and evaluation-Volume 3: Physical properties.Strategic Highways Research Program, Rep.No.SHRP-A-369[R], National Research Council, Washington, D.C. 1994: 43-79.

Dynamic performances of asphalt mortar based on fractional derivatives

LI Ruiduo1,2, YUE Jinchao1, LI Ruixia1, YAO Liyang2

(1. School of Water Conservancy and Environment, Zhengzhou Univ., Zhengzhou 450002, China;2. School of Transportation Engineering, Henan University of Urban Construction, Pingdingshan 467036, China)

Asphalt mortars were prepared with different ratios of filler bitumen of 0.62, 0.82, 1.02, 1.22 and 1.44. Then the dynamic behaviors of asphalt mortars at 20℃, 30℃, 40℃ and 50℃ were studied with a dynamic shear rheometer. The relationships among complex modulus, rutting resistance factor and phase angle udner different ratios of filler bitumen and test temperatures were studied. The relationships between Nutting creep equation and Abel sticky pot creep model of classic fractional order derivatives were established based on the theory of fractional derivatives. The dynamic responses of fractional order Riemann-Liouville operator viscoelastic creep constitutive model were analyzed. The model parametersAandγwere determined using the results of dynamic shear rheological tests.

asphalt mortar; ratio of filler bitumen; dynamic shear rheological tests; fractional derivative;Nutting creep equation; deformation factor; viscoelastic factor

河南省科技攻关计划(112102310602)；教育部“长江学者和创新团队发展计划”创新团队(IRT1186)；水利与交通基础设施安全防护河南省协同创新中心(2012-6)

2015-09-21修改稿收到日期：2016-01-09

李锐铎 男，博士生，讲师，1980年生

乐金朝 男，博士，教授，博士生导师，1965年生

E-mail: yuejc@zzu.edu.cn

U414

A

10.13465/j.cnki.jvs.2016.15.008