驱动工况下高速动车组蛇行失稳非线性度

陈双喜, 董大伟, 邓小军, 林建辉

(1. 西南交通大学 机械工程学院,成都　610031; 2. 中车青岛四方机车车辆股份有限公司国家工程中心,山东 青岛　2661113.西南交通大学 牵引动力国家重点实验室,成都　610031)



驱动工况下高速动车组蛇行失稳非线性度

陈双喜1,2, 董大伟1, 邓小军2, 林建辉3

(1. 西南交通大学 机械工程学院,成都610031; 2. 中车青岛四方机车车辆股份有限公司国家工程中心,山东 青岛2661113.西南交通大学 牵引动力国家重点实验室,成都610031)

基于信号的波内调制现象定义信号的非线性指标，并研究高速动车组在驱动工况下(驱动系统在直接转矩控制下)蛇行失稳的非线性特征。首先建立包括高速动车组的车辆动力学Simpack子模型和牵引传动系统的直接转矩控制Matlab/Simulink子模型在内的机械电气耦合联合仿真模型，然后计算动力学响应，最后基于黄变换计算列车在蛇行失稳状态下动力响应的非线性指标变化。仿真结果表明：若列车出现蛇行失稳，转向架和车体横向振动非线性指标会急剧增大；完全失稳情况下，车体横向加速度非线性度大于0.1，转向架横向位移非线性度大于0.3。

黄变换；非线性度；高速动车组；蛇行失稳

车辆系统中的非线性因素主要有轮轨接触几何的非线性、轮轨接触蠕滑力的非线性、悬挂刚度和阻尼的非线性等[1-2]。轮轨接触关系由踏面外形和钢轨外形几何参数决定。车轮不同踏面如锥形踏面、LMA踏面、XP55踏面等踏面，以及车轮外形和钢轨外形磨损后，轮轨接触点位置、接触角、侧滚角、接触面曲率半径均非线性变化。当轮对左右移动或者轨道高低、方向、扭曲等平顺情况下，轮轨接触点位置、接触角、侧滚角、接触面曲率半径、钢轨作用点的位置、踏面等效锥度等参数均非线性变化。事实上，车轮轮缘常常贴近钢轨，接触几何关系具有非常明显的非线性关系。轮轨接触一般先采用Kalker线性理论[3]来描述，然而该理论值适合于小蠕滑率和小自旋情况，即轮轨接触面主要由黏着区控制。对于轮轨接触面主要由滑动去控制的大蠕滑甚至全滑动情况，蠕滑力的线性关系被打破，蠕滑率不断增大，最后趋于库仑摩擦力饱和极限。为此，需要用非线性蠕滑理论[4]进行修正，使轮轨蠕滑力可广泛实用于任意蠕滑率情况。

线性系统总可以应用叠加原理，系统对不同激励的响应可以线性相加，而非线性系统叠加原理不成立，因此非线性系统的研究复杂得多。在研究方法上，非线性振动与线性振动之间有本质区别。在非线性振动的研究中，很难得到微分方程的解析解。非线性振动基本研究方法有定性方法和定量方法。定性方法主要研究已知解领域内系统的稳定性，定量方法主要关心运动的时间历程，一般采用摄动法求解得到近似解。我们也可以采用数字分析方法来求解非线性振动问题。其基本步骤是对非线性系统进行数值积分，在时域内把响应的时间历程离散化，对每一个时间步长内按照线性系统进行计算，并对每一步计算结果进行修正。由于非线性分析理论发展的不完善，很多问题还无法进行理论上的分析，而数值分析理论的发展和计算工具性能的提高使得数值仿真成为可能。本文基于信号的波内调制现象定义信号的非线性指标，建立包括高速动车组的车辆动力学非线性Simpack模型和牵引传动系统的直接转矩控制Matlab/Simulink模型在内的机械电气耦合联合仿真模型，研究在驱动工况(牵引系统直接转矩控制)下，高速动车组蛇行失稳动力响应的非线性度，并研究如何利用非线性度来衡量列车蛇行失稳状态。

1　基于黄变换的非线性度分析

根据线性代数的知识，线性系统是状态变量和输出变量对于所有可能的输入变量和初始状态都满足叠加和放大原理的系统。例如对于两个输入变量x1(t)和x2(t)，输出变量y1(t)=H{x1(t)}和y2(t)=H{x2(t)}，若满足：

αy1(t)+βy1(t)=H{αx1(t)+βx1(t)}

(1)

式中:(α，β是放大系数)，那么该系统是线性系统。由于该准则依赖初始条件和载荷情况，现实中并不可行。这是因为现实中的系统要复杂得多，输入和输出很难量化。1998年Huang[5]首先提出经验模态分解EMD和Hilbert谱分析。作为一种新的自适应数据分析方法，其目的是有效提取非线性非稳态数据的时频分布。经验模态分解EMD是为了能够使Hilbert变换能定义瞬时频率。最初Huang运用Hilbert变换定义瞬时频率，后来它发现Hilbert变换不满足Bedrosian 理论和Nuttall理论，提出了正交化的Hilbert变换(NHT)[6]、DQ方法[6]来计算时频幅值谱。Huang[5]提出基于信号的波内调制现象来定义信号的非线性度。波内频率调制定义为瞬时频率与广义Zero-crossing频率之差[6]。在最近的研究中，Huang建议将非线性度定义为

(2)

本文中，定义非线性指标为：

(3)

式中：IF(t)为瞬时频率，IFzc(t)为广义Zero-crossing(GZC)频率，而非瞬时频率，它能描述信号波内部的频率调制；Azc(t)为瞬时幅值。本文采用DQ方法计算局瞬谱。

对于简单的非线性振动方程，如无阻尼系统的杜芬方程：

(4)

当方程有周期解时，通过摄动法，得到方程的解为：

x(t)=(A0+εA1+ε2A2)cost+

(5)

x(t)=cos(t+δsin2t)=

(6)

那么方程(5)和(6)是一致的，方程(6)中x(t)很明显是波内频率调制信号，即非线性方程的解是频率调制的。假定方程中的系数ε=1，γ=0.1，Ω=0.2 Hz，100 s内该方程的解如图1所示，波形存在明显的非线性特征。

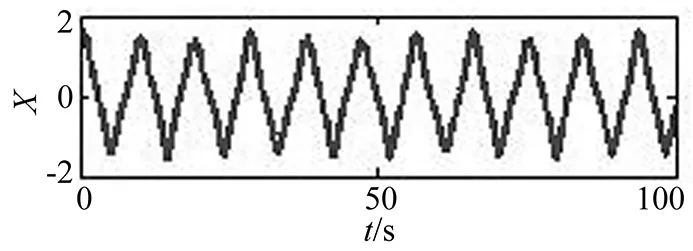
图1　杜芬方程的解(ε=1，γ=0.1，Ω=0.2 Hz)Fig.1 Solution of duffing equation

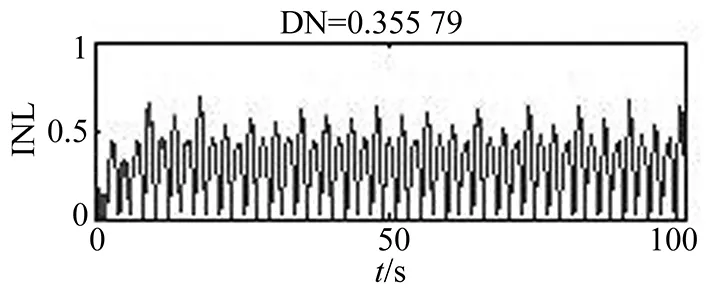
图2　杜芬方程解非线性指标Fig.2 Index of nonlinearity for duffing equation solution

根据式(2)计算杜芬方程解(图1)的非线性度DN=0.36(图2),表现出极强的非线性特征。计算表明，当ε=1、2、5、10、20，DN分别为0.36、0.24、0.16、0.14、0.13，解的非线性度DN随着ε则快速减小。下面尝试用此方法研究复杂的动车组非线性振动响应。

2　动车组机电耦合仿真模型

一般情况下，假定车辆动力学模型为恒定的速度，即便是牵引工况也很少考虑牵引系统的控制策略[7]，为了充分考虑牵引和制动对列车动力学的影响，本文从牵引系统的角度建立机电耦合的联合仿真模型。针对我国更高速试验动车组，首先建立列车的车辆动力学模型，然后建立动车组牵引传动系统的直接转矩控制系统[8]的Matlab/Simulink仿真模型，并通过接口模块将两个系统连接起来，从而建立起直接转矩控制下列车运行的机电耦合模型。

首先在Simpack软件中建立高速动车组的动力学模型，包括三节车，每节车包括两个构架、四个轮对、八个轴箱、四个电机(电机轴)、四个齿轮箱(输入输出轴)、两个牵引拉杆，如图3所示。轮对、转向架、车体和电机均有纵向、横向、垂向、侧滚、点头和摇头六个自由度；电机悬挂在构架上；齿轮箱一端悬挂在构架上，另一端在车轴上。一系二系悬挂采用弹簧单元模拟。运用弹簧单元模拟牵引拉杆连接车体和构架；阻尼单元模拟抗蛇行减振器、横向和垂向减振器和车间减振器。车钩之间和横向止挡用非线性弹簧模拟。车轮直径0.92 m，踏面为LMA，钢轨为中国轨道60 kg/m。

图3　动车组车辆动力学模型Fig.3 Dynamics model of EMU

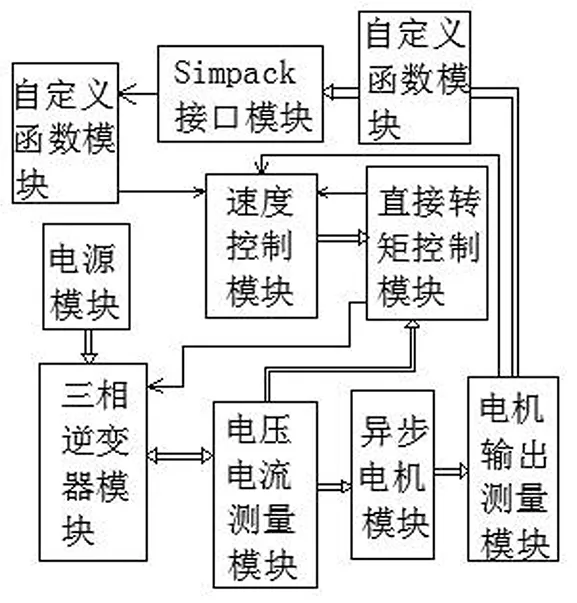
图4　动车组机电耦合模型简图Fig.4 Electromechanical coupling model of EMU

然后根据各个部分的工作原理搭建了高速动车组牵引传动系统的Matlab/simulink与simpack动力学联合仿真模型，整个系统简图如图4所示，包括：电源模块、三相逆变器模块、测量模块、异步电动机模块、直接转矩控制模块(DTC)、速度控制模块和simpack接口模块。直接转矩控制模块由转矩给定、磁通给定，电流和电压输入信号都经过采样开关，DTC模块包括转矩和磁通计算、滞环控制、磁通选择、开关表、开关控制等单元。DTC模块是输出三相逆变器开关器件的驱动信号。在Simpack接口模块中，测量列车运行速度并反馈到电机模块，同时通过自定义函数(牵引特性曲线)计算给定扭矩。自定义函数根据速度计算列车的运行阻力，并通过接口模块加载到列车车体上。异步电动机模块输出的电磁转矩通过接口模块，作为扭矩输入加载到车辆动力学模型中的电机转子轴上，并经齿轮箱传递到车轴上驱动列车前进。于是整个模型就完成了。可用此模型计算列车从启动到停止全过程中机械系统和电气系统的响应。鉴于本文重点并非机电耦合模型，模型详细介绍省略。

3　蛇行失稳动力响应的非线性度分析

假定列车运行在直线轨道上，轨道为干轨，摩擦系数μ=0.3。根据动力学计算已知：在正常情况下，列车蛇行失稳临界速度大于700 km/h；在每个转向架失效一个抗蛇行减振器情况下，临界速度仍然大于650 km/h；而在所有转向架单侧抗蛇行减振器都失效情况下，临界速度大幅降低到262 km/h。为了得到蛇行失稳状态，本文假定所有转向架单侧抗蛇行减振器都失效。下面首先计算列车从启动到300 km/h(大于蛇行失稳速度262 km/h)并运行一段时间后减速到零全过程的动力学响应，然后分析失稳过程中加速度响应的非线性指标变化情况。

给定列车首先从t=0，速度1 km/h(为了防止速度过小导致无法计算蠕滑力，速度没有设置为0)加速到最高运行速度300 km/h，运行250 s后开始减速到1 km/h。转速给定使用simulink离散控制模型库中的timer模块，设定值为：t=0、250、500 s时转速分别为3 476、12、12 r/min。耦合模型将根据给定的转速计算磁链、给定转矩、逆变器变频变压电压并产生电磁转矩驱动轮对运行。需要指出的是：由于对电机采用了直接转矩控制技术，列车实际转速并非为给定转速，而是在跟踪给定转速，因此总是在给定转速附近波动；电机输出电磁转矩也是在理论输出转矩附近大幅波动，这是由变频变压的逆变器决定的。模型采用混合步长的离散算法，基本仿真步长Ts=1×10-5s，转速调节器仿真步长为140×10-6s，动力学模型仿真步长为0.001 s。因本文重点在动力学响应，故不对系统的电气响应如电压、电流、磁链、电磁扭矩等进行讨论。

在牵引系统直接转矩控制下，中间车前转向架的横向振动加速度与速度如图5所示。列车从零加速开始加速前进，转向架横向加速度一直很小(小于0.05 m/s2)；当运行130 s后，列车运行速度达到临界速度262 km/h，转向架横向加速度开始逐渐增大，列车出现小幅度蛇行失稳；从130 s到152 s的20 s范围内，加速度在0.5 m/s2附近波动，列车处于失稳的第一阶段；运行152 s后，列车运行速度达到292 km/h，转向架横向加速度进一步增大(大于5 m/s2)，列车完全蛇行失稳(失稳第二阶段)；运行250 s后，即驱动转矩反向后，列车开始以较大加速度减速，转向架横向加速度开始逐渐减小(失稳第三阶段)；运行276 s后速度降到233 km/h，横向加速度减小到0.05 m/s2，列车从蛇行失稳状态消失。

目前国内判断列车蛇行失稳通常采用这样的处理方法："对列车转向架横向振动加速度进行0.5～10 Hz带通滤波，若滤波后的信号连续6个波峰值大于8～10 m/s2，则认为列车蛇行失稳。若依此方法对图5的横向加速度进行计算判别(计算过程略)，列车并没有蛇行失稳。但是很明显，列车确实已经蛇行失稳了。因此，该方法判别列车蛇行失稳并不准确。下面从非线性特征角度研究蛇行失稳。

图5　转向架横向加速度(0～300 km/h)Fig.5 Lateral acceleration of bogie(0～300 km/h)

图6给出了列车从蛇行失稳前到完全失稳(120 s～160 s)过程中的转向架横向振动加速度的局部瞬时谱和非线性指标INL的变化情况。从图6(a)可以看出，从130 s开始，列车运行速度达到临界速度262 km/h，局部瞬时谱在2 Hz附近出现大波动特征频率，该频率与理论蛇行频率一致，系统开始出现蛇行失稳迹象；152 s开始，特征频率波动有所减小，但幅值增大(颜色变深)，系统完全失稳。蛇行失稳第一阶段虽然振动幅值很小，但是频率波动稍大。从图6(b)看出，蛇行失稳出现后，虽然振动幅值很小(小于1 m/s2)，INL指标却迅速增大超过0.2；152 s后完全失稳阶段，振动幅值增大10倍，INL指标增大到超过0.4。图7给出了车体横向加速度的局部瞬时谱和非线性指标，蛇行失稳出现时刻(130 s)，非线性指标INL就迅速增大到超过0.4；152 s后的完全失稳阶段，INL则没有明显变化。因此，非线性指标INL对蛇行失稳非常敏感，只要列车出现蛇行失稳，其数值就大幅增加。

从图6和图7可知，虽然转向架和车体横向加速度的非线性指标均能揭示列车蛇行失稳。但是从数据处理角度来讲，用车体数据来计算能减少计算量。这是因为转向架的高频频率成分比车体多，而蛇行频率在低频段，黄变换信号分解总是先分解出高频成分，用车体计算能减少信号分解次数。因此，建议用车体数据进行计算非线性指标和非线性度。

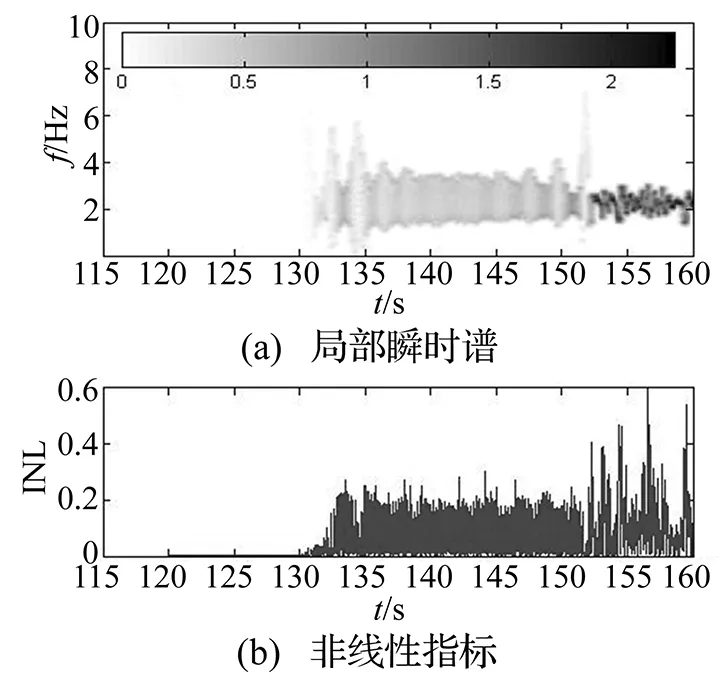
图6　转向架横向加速度非线性分析(0～300 km/h)Fig.6 Nonliearity analysis for lateral acceleration of bogie

图7　车体横向加速度非线性分析(0～300 km/h)Fig.7 Nonliearity analysis for lateral acceleration of car body

表1给出了列车在完全失稳阶段，不同速度工况下，车体横向加速度的非线性度DN的变化情况。非线性度DN计算的时间长度均为10 s。列车在300 km/h完全失稳状态下(从180 s～240 s)，车体横向加速度非线性度DN为0.14；列车在350 km/h完全失稳状态下(从220 s～290 s)，车体横向加速度非线性度DN在0.15-0.18范围波动；列车在400 km/h完全失稳状态下(从300 s～380 s)车体横向加速度非线性度DN在0.18～0.24范围波动。可见，列车在完全蛇行失稳状态下，车体横向振动DN大于0.1，且随速度增加而增大。

图8给出了所有转向架单侧抗蛇行减振器都失效工况下，列车从启动加速到不同最高运行速度(300 km/h、350 km/h、400 km/h)再到减速停止过程中，转向架和车体横向位移的非线性度DN变化情况。列车完全失稳后，转向架和车体的非线性度DN均大幅度增大，转向架的DN大于车体，且随速度增加而增大。速度从300 km/h增大到400 km/h，转向架横向位移DN最大值从0.35增大到0.5，甚至大于第一节图1中杜芬方程解的非线性度，表现出极强的非线性特征；而车体横向位移DN始终在0.1附近。

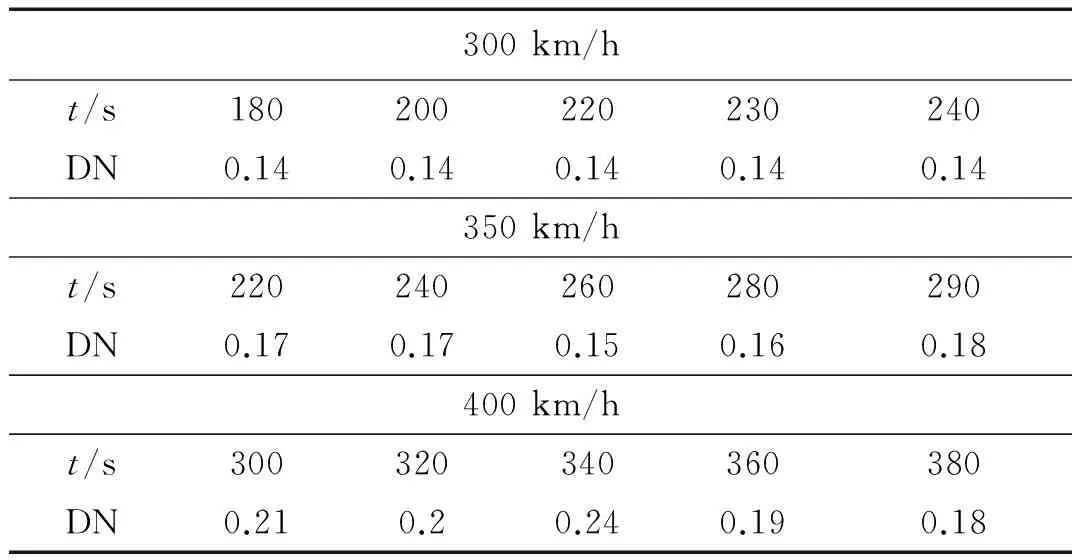
表1　车体横向加速度非线性度

图8　不同速度下位移响应非线性度Fig.8 DN for displacement response at different speed

根据车辆动力学理论，蛇行运动的非线性稳定性通常采用Hopf分叉理论来分析：如果其极限环幅值出现分叉，则列车蛇行运动失稳，极限环幅值分叉点即为理论临界速度点。而实际临界速度常用的计算方法为：给定一段有限长的实际轨道随机不平顺激扰样本函数，首先让列车运行在不平顺轨道上并激发其振动，然后让列车运行在理想光滑轨道上，通过观察系统的振动能否衰减到平衡位置，来判断系统是否出现蛇行失稳。如果在某一车速下系统的振动不再收敛到平衡位置，这时的车速值即为系统的实际临界速度。若列车出现蛇行失稳，最直接能观察到的现象是轮对横向位移不再收敛到平衡位置。失稳后转向架横向振动加速度幅值也会增大，目前的蛇行判定方法也是根据滤波后的振动峰值来定义，然而该方法并不准确。

本文通过对振动响应非线性度的分析可观察到这样现象：若列车开始蛇行失稳，转向架和车体横向振动非线性指标INL会急剧增大；若完全失稳，车体横向加速度非线性度DN大于0.1，转向架横向位移非线性度DN大于0.3。因此，我们可建议根据这样的特征来判别列车是否失稳: 若车体横向加速度非线性度大于0.1或转向架横向位移非线性度大于0.3，列车完全蛇行失稳。

4　结　论

笔者建立了包括高速动车组的车辆动力学子模型和牵引传动系统的直接转矩控制子模型在内的机电耦合模型，计算了列车从启动到完全失稳再到减速停止全过程中的动力学响应，基于黄变换计算动车组动力响应的非线性指标。分析结果表明基于黄变换的非线性指标能清晰揭示列车的非线性振动特征的变化，可作为衡量列车失稳的指标，并且给出了判别蛇行失稳的参考方法。

[1] Kalker J J. On the rolling contact of two elastic bodies in the presence of dry friction[D]. The Netherland, Delft University, 1976.

[2] Kalker J J. Simplified theory of rolling contact[R]. Delft pregress Report 1, 1973:1-10.

[3] Kalker J J. A fast algorithm for the simplified theory of rolling contact[J]. Vehicle System Dynamics, 1982, 11:1-13.

[4] Shen Z Y, Hedrick J K, Elkins J A. A comparison of alternative creep force models for railway vehicle dynamic analysis[J].Proceedings of 8th International Association for Vehicle System Dynamics(IAVSD) Symposium, MIT, Cambridge,1983,12(1/2/3):79-83.

[5] Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the hilbert spectrum for nonlinear and nonstationary time series analysis[J]. Proc Royal Society London A, 1998,454(1971):903-995.

[6] Huang N E, Wu Z, Long S R, et al. On instantaneous frequency[J]. Advances in Adaptive Data Analysis, 2009(1): 177-229.

[7] 王永冠. 驱动工况下机车动力学仿真[D]. 成都：西南交通大学，2005.

[8] Depenbrock M. Direkte selbstregelung(DSR) fuhrhochdy-namische drefeldantriebe mit stromrichterpeisung[J]. ETZarchiv, 1985，7(7):211-218.

[9] 余丹萍. CRH3型动车组牵引传动系统的直接转矩控制研究[J].机电工程，2010,27(10)：62-67.

YU Dan-ping. Research of direct torque control on traction drive system of CRH3 EMU[J]. Journal of Mechanical & Electrical Engineering,2010,27(10)：62-67.

Nonlinearity index for hunting instability of high-speed EMUs with a drive system

CHEN Shuangxi1,2, DONG Dawei1, DENG Xiaojun2, LIN Jianhui3

(1. College of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031, China; 2. National Engineering Center, CRRC Qingdao Sifang Co., Ltd, Qingdao 266111, China;3. State Key Laboratory of Power Traction, Southwest Jiaotong University, Chengdu 610031, China)

The nonlinearity index of signals was defined based on intra-wave modulation and the nonlinear characteristics for hunting instability of high-speed EMUs with a drive system controlled with a direct torque were studied. Firstly, an electromechanical coupling co-simulation model including a vehicle dynamic Simpack submodel of high speed EMUs and a Matlab/Simulink submodel of drive system controlled with a direct torque was built. Then the EMU’s dynamic responses were calculated. Finally, the nonlinearity index of the dynamic responses was calculated based on Huang transformation. The simulation results indicated that when the EMU’s hunting motion instability happens, the nonlinearity indexes for lateral vibrations of bogie and car body increase dramatically, the nonlinearity indexes for car body lateral acceleration and bogie lateral displacement are larger than 0.1 and 0.3, respectively under the full unstable condition.

Huang transformation; degree of nonlinearity; high speed EMU; hunting instability

中央高校基本科研业务费专项资金资助(SWJTU10ZT04)

2015-02-25修改稿收到日期：2015-08-17

陈双喜 男，博士后，1982年生

U270.1

A

10.13465/j.cnki.jvs.2016.15.007