自适应最优化窄带分解方法及其应用

彭延峰, 程军圣, 杨　宇, 李宝庆

(湖南大学 汽车车身先进设计制造国家重点实验室,长沙　410082)



自适应最优化窄带分解方法及其应用

彭延峰, 程军圣, 杨宇, 李宝庆

(湖南大学 汽车车身先进设计制造国家重点实验室,长沙410082)

提出了自适应最优化窄带分解(Adaptive Optimization Narrow-Band Decomposition，AONBD)方法。该方法将信号分解转化为对滤波器参数的优化问题，以得到信号的最优化解为优化目标，在优化过程中将信号自适应的分解成多个内禀窄带分量(Intrinsic Narrow-Band Components，INBC)。AONBD分为两步，首先通过优化得到最优的滤波器，然后使用该滤波器对信号进行滤波以得到信号的最优化解。阐述了AONBD的基本原理及分解步骤。采用仿真信号将AONBD方法与自适应最优化时频分析(Adaptive Sparsest Time-Frequency Analysis，ASTFA)方法及经验模态分解(Empirical Mode Decomposition，EMD)方法进行对比。结果表明，AONBD在抑制端点效应和模态混淆、抗噪声性能、提高分量的正交性和准确性等方面具有一定的优越性。对转子振动信号的分析结果表明，AONBD能有效应用于机械故障诊断。

自适应最优化窄带分解；内禀窄带分量；局部窄带信号；奇异局部线性算子；转子故障诊断

非平稳信号的分析处理方法是现代信号处理领域中的一个研究热点。经验模态分解(Empirical Mode Decomposition，EMD)方法[1-3]是近年来最具代表性的自适应时频分析方法之一，但仍存在端点效应和模态混淆等缺点。

在EMD的基础上，Thomas等[4]提出了一种使用高斯牛顿迭代法解决非线性优化问题的自适应最优化时频分析(Adaptive Sparsest Time-Frequency Analysis，ASTFA)方法。该方法将信号分解问题转化为非线性约束优化问题，优化目标为得到非线性信号的最优化表示[5-7]，约束条件是所有内禀模态函数(Intrinsic Mode Functions，IMF)[8]都处于过完备字典库Dic中。ASTFA无需处理极值点，所以在抑制端点效应和模态混淆等方面优于EMD。但ASTFA仍存在一些不足。①若原始信号为N维向量，则ASTFA需要同时对3N个参数进行优化。当原始信号维数较大时，使用ASTFA进行信号分解会产生很大的计算量。②由于使用高斯牛顿迭代法进行优化，且高斯牛顿迭代法对初始值的要求较高。所以，当信号较为复杂时，若初始值设置不恰当，则使用ASTFA进行分解时就不能得到准确的IMF分量。

针对ASTFA方法的缺陷，本文提出自适应最优化窄带分解方法(Adaptive Optimization Narrow-Band Decomposition，AONBD)。AONBD的实质是对原始信号进行滤波。首先设计了滤波器χ(k|λ)，通过对滤波器χ(k|λ)的参数λ进行优化得到信号的最优化解。该方法将ASTFA中对原始N维信号中所有元素的优化过程转化为对参数λ的优化过程，避免了ASTFA中优化参数的个数随信号长度变化的问题，大大减少了计算量。其次，AONBD使用遗传算法(Genetic Algorithm，GA)进行优化，随机生成初始种群，避免了ASTFA中初始值设置的问题。此外，AONBD在优化目标函数中加入奇异局部线性算子，将每个分量约束为局部窄带信号[9-10]，相对ASTFA，其物理意义更明确。

本文阐述了AONBD方法的基本理论和迭代步骤，采用仿真信号将其与ASTFA方法和EMD方法进行了对比。结果表明，该方法能更有效抑制端点效应和模态混淆，并在抗噪声性能，准确性和正交性方面具有优越性。使用仿真信号对三种方法的整体耗时进行了对比。结果表明，AONBD的整体耗时要低于ASTFA，但仍高于EMD。使用AONBD对转子故障振动信号进行分析，结果表明该方法能有效应用于机械故障诊断。

1　AONBD

1.1ASTFA

ASTFA方法可以用两个步骤来描述：

① 建立过完备字典库Dic：

Dic={a(t)cos(θ(t)):θ′(t)≥0,

a(t)∈V(θ)}

(1)

k=0,…μn,l=1,…μn}

(2)

式中：θ′(t)≥0是为了保证瞬时频率具有物理意义，约束a(t)∈V(θ)的目的是使a(t)比cos(θ(t))更平滑，Span为空间内所有元素的线性张成。

② 建立过完备字典库Dic后，为寻找最佳的内禀稀疏结构，将信号分解问题转换成非线性有约束优化问题P1，进而得到信号的最优化解。信号的迭代过程如下：

(1) 令r1(t)=f(t)。其中f(t)为原始信号。

(2) 解决优化问题P1：

Subject to:IMFi(t)∈Dic

(3)

式中：IMFi(t)为ASTFA方法分解得到的第i个分量。

(3) 令ri+1(t)=ri(t)-IMFi(t)。

ASTFA使用高斯牛顿迭代法解决最小二乘问题P1，而高斯牛顿迭代法对初始值的要求较高。若初始值偏离真实值太远，则目标函数在迭代后发散，不能得到准确的IMF分量。并且，由于需要同时对IMFi(t)中所有元素进行优化，当f(t)维数较高时会产生很大的计算量，时效性较差。

1.2AONBD的基本原理

1.2.1内禀窄带分量

信号s(t)一般能够表示为A(t)cos(ωt+φ(t))的形式。如果A(t)是带限的，它的最大频率远小于ω，且φ(t)是“缓变”相位函数，则信号s(t)称为窄带信号。窄带信号的概念可以推广到局部窄带信号。如果对于s(t)的任一时间点，都存在一个邻域区间，使得s(t)在该区间中近似于窄带信号，则信号s(t)称为局部窄带信号。

若信号分解得到的分量满足局部窄带信号的条件，本文称其为内禀窄带分量(Intrinsic Narrow-Band Components，INBC)。

1.2.2奇异局部线性算子

从L2(R)到L2(R)的线性算子T称为局部线性算子。若∀t∈R，存在t的领域Bt，使得

T(s)(t)=T(s|Bt)(t),(∀s∈L2(R))

(4)

式中：s|Bt表示s在Bt上的限制。若T是奇异的，称T为奇异局部线性算子。本文使用的奇异局部线性算子如下:

(5)

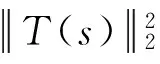
1.2.3AONBD的步骤

AONBD方法将信号分解问题转换成非线性无约束优化问题P2，并得到信号的最优化解。信号的迭代过程如下：

(1) 令r1(t)=f(t)。

(2) 解决优化问题P2：

P2：Minimize

(6)

式中：INBCi(t)为AONBD方法分解得到的第i个分量。D是微分算子，用于规范化INBCi(t)。由于使用了规范化的奇异局部线性算子，ASTFA中的有约束非线性优化问题被转化为无约束非线性优化问题。

(3) 令ri+1(t)=ri(t)-INBCi(t)。

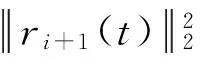
设f(t)为N×1向量，若使用ASTFA中的优化方法解决优化问题P2，则需要同时对N个参数进行优化，计算量极为巨大[4]。为减小计算量，使用基于快速傅里叶变换(Fast Fourier Transform，FFT)的迭代过程解决优化问题P2：

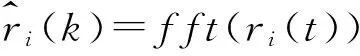
② 令λ=[ωb,ωc]，简单带通滤波器χ(k|λ)如下：

(7)

对仿真信号及试验信号的分析表明，使用式(7)所示滤波器时AONBD方法仅适于周期信号的分析。因此，为处理非线性、非平稳信号，令λ=[ω,ωb,ωc]，建立滤波器χ(k|λ)如下：

χ(k|λ)=

(8)

③ 解决非线性无约束优化问题P3：

P3：Minimize

(9)

本文使用MATLAB自带的GA程序对滤波器χ(k|λ)中λ包含的三个参数进行优化，GA的最大进化代数设置为200，种群大小设置为20，其它参数使用MATLAB中的默认参数。GA随机生成初始种群，避免了ASTFA中初始值设定的问题。

④ 得到最优参数λo后，令

(10)

上述基于FFT的迭代过程将ASTFA中对原始数据N个点的优化过程转变成对滤波器参数λ的优化过程，大大减少了运算量。

2　信号仿真与对比分析

考虑如下仿真信号：

(11)

式中：x1(t)由调幅调频信号和简单正弦信号组成，n(t)表示两段间歇噪声信号，每段间歇信号的长度为0.1 s，信噪比为15 dB。混合信号x(t)由x1(t)和n(t)组成，信号的时域区间为[0,1]。混合信号x(t)及其分量的时域波形如图1所示。图1(a)为x(t)的时域波形，(b)为x1(t)中的调幅调频分量，(c)为x1(t)中的简单正弦分量，(d)为间歇噪声信号n(t)。

图1　混合信号x(t)及其分量的时域波形Fig.1 The time-domain waveforms of mixed signal x(t) and its components

分别采用AONBD、ASTFA和EMD对x(t)进行分解。为了对比，对原始信号进行端点波形延拓[11]。AONBD、ASTFA和EMD的分解结果分别如图2～图4所示。分解得到的第一个分量和第二个分量分别对应x1(t)中的调幅调频分量和简单正弦分量。

图2　混合信号x(t)的AONBD分解结果Fig.2 The decomposition results generated by AONBD of mixed signal x(t)

图3　混合信号x(t)的ASTFA分解结果Fig.3 The decomposition results generated by ASTFA of mixed signal x(t)

从图2～图4可以看出，AONBD分解出来的分量幅值较为平稳并与真实值更接近，其残余量和噪声信号的误差较小。由于间歇噪声信号的干扰，ASTFA和EMD分解出来的分量都出现了一定的误差，尤其是EMD的分解结果出现了严重的模态混淆。

图4　混合信号x(t)的EMD分解结果Fig.4 The decomposition results generated by EMD of mixed signal x(t)

为了量化地比较三种方法的分解结果，本文考虑参数：分量的能量误差Ei、相关性系数ri[12]、正交性指标IOjk[13]及分解时间T。由三种方法得到的分量的上述参数如表1所示，其中Ei和ri是分解得到的第i个分量与其相对应的真实值之间的比较结果，IOjk为分解得到的第i个分量和第j个分量之间的正交性指标。分析结果表明，与ASTFA和EMD相比，AONBD的能量误差更小，且拥有更好的相关性和正交性。因此，AONBD对噪声干扰引起的模态混淆有很好的抑制作用，分解得到的信号更准确。由于拥有更好的正交性，AONBD的能量泄露更小。且相对ASTFA，AONBD的分解速度更快。

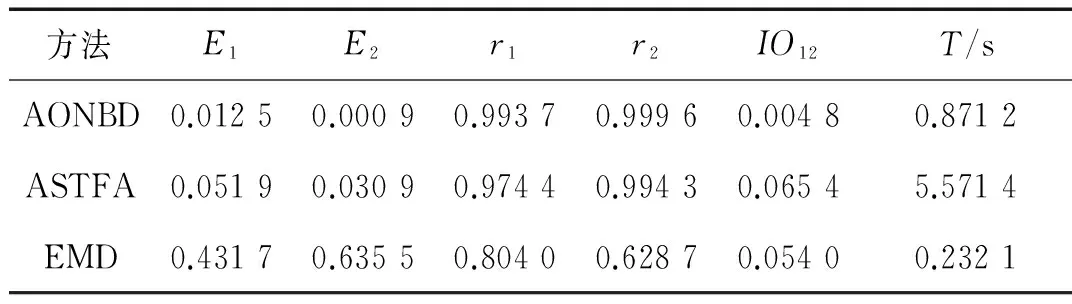
表1　AONBD、ASTFA和EMD的参数对比(SNR=15)

为了证明AONBD相对ASTFA和EMD能更有效的抑制端点效应，在未处理端点效应时对混合信号x(t)进行分解，结果分别如图5～图7所示。可以看出，相对EMD，AONBD和ASTFA分解结果的端点效应更小。可见由于需要处理极值点，EMD受端点效应的影响更大，其端点效应更严重。

图5　混合信号x(t)的AONBD分解结果(未处理端点效应)Fig.5 The decomposition results generated by AONBD of mixed signal x(t)(end effect is not handled)

图6　混合信号x(t)的ASTFA分解结果(未处理端点效应)Fig.6 The decomposition results generated by ASTFA of mixed signal x(t)(end effect is not handled)

图7　混合信号x(t)的EMD分解结果(未处理端点效应)Fig.7 The decomposition results generated by EMD of mixed signal x(t)(end effect is not handled)

为了证明AONBD相对ASTFA和EMD具有更好的抗噪声性能，在混合信号x(t)的信噪比为20和25时，使用三种方法分别对信号进行分解，得到的分量的参数如表2和表3所示。

表2　AONBD、ASTFA和EMD的参数对比(SNR=20)

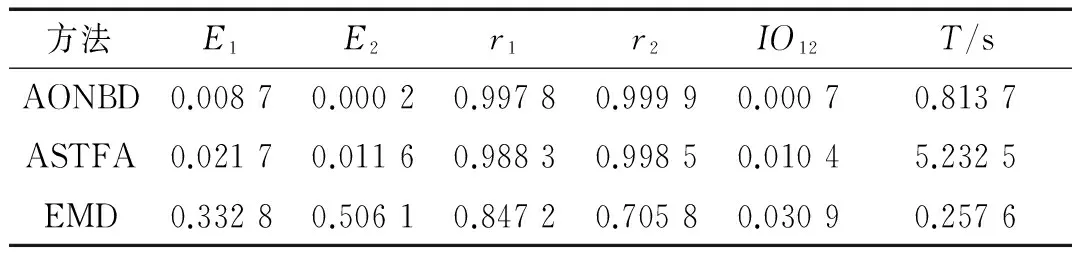
表3　AONBD、ASTFA和EMD的参数对比(SNR=25)

由表2和表3可知，在不同的噪声强度下，AONBD分解得到的结果仍然拥有更好的准确性和正交性。同时，和ASTFA相比，AONBD的分解速度更快。

3　整体耗时对比分析

考虑如下简单信号：

(12)

仿真信号x(t)由两个简单余弦信号混合而成，其时域区间为[0,1]。混合信号的时域波形如图8所示。为对AONBD、ASTFA及EMD的整体耗时进行分析，令x(t)的采样频率分别为512 Hz、1 024 Hz、2 048 Hz、4 096 Hz、8 192 Hz。使用三种方法对不同采样频率下的信号进行分解，得到第一个分量和第二个分量所耗时间如表4和表5所示。

图8　混合信号y(t)及其分量的时域波形Fig.8 The time-domain waveforms of mixed signal y(t) and its components

方法T/s512Hz1024Hz2048Hz4096Hz8192HzAONBD0.18050.56200.63960.78910.9532ASTFA0.27170.58690.72111.01471.9059EMD0.04680.07240.14510.45060.8573

由表4及表5可知，首先，由于使用了优化算法AONBD及ASTFA的整体耗时比EMD更长。其次，相对ASTFA，AONBD的整体耗时较低且受采样频率的影响更小。这是因为AONBD对滤波器χ(k|λ)中λ包含的三个参数进行优化，其优化参数的数目是不变的，而ASTFA方法的优化参数的数目随着采样频率的增加而增加。

表5　AONBD、ASTFA和EMD的耗时对比(第二个分量)

4　AONBD方法在转子故障诊断中的应用

为了验证AONBD方法的实用性，将其应用于转子系统碰摩故障诊断[14-15]，振动信号的采样频率为4 096 Hz，工频f0为50 Hz。图9为转子径向位移振动信号的时域波形。振动信号的包络谱分析[16]结果如图10所示，可知信号的主要频率成分只有工频和其2倍频，其它和碰摩故障有关的高频或分频信息全部被噪声和背景干扰所淹没，无法识别出。

图9　碰摩故障的转子径向位移振动信号Fig.9 The radial displacement vibration signal of the rotor with rubbing fault

图10　转子径向位移振动信号的包络谱Fig.10 The envelope spectrum of the radial displacement vibration signal of the rotor

图11　转子径向位移振动信号的AONBD分解结果Fig.11 The decomposition results generated by AONBD of the radial displacement vibration signal of the rotor

图12　图10中分量的包络谱。(a)、(b)和(c)分别对应INBC1、INBC2和INBC3的包络谱Fig.12 The envelope spectrum of the components in Fig.10.(a)，(b) and(c) the envelope spectrum of INBC1、INBC2 and INBC3 respectively

图11为对振动信号进行AONBD分解得到的结果，INBC1、INBC2和INBC3的包络谱分别如图12(a)、(b)和(c)所示。转子每旋转一周，动、静件就摩擦一次，因此调幅信号中调制波的频率存在工频成分[17-19]。同时，转子发生碰摩故障时，频谱上还会存在非常丰富的高次谐波成分，严重摩擦时，还会出现分频成分。由图12可知，AONBD方法有效分解出了倍频成分INBC1、工频成分INBC2和分频成分INBC3，符合转子碰摩故障的特征，说明了AONBD方法识别机械故障的有效性。

5　结　论

AONBD方法是一种新的基于ASTFA方法和奇异局部线性算子的自适应分解方法，可以用于非平稳、非线性信号的处理。相对ASTFA和EMD，AONBD具有以下优点：

(1) ASTFA需要对原始数据所有的点进行优化，而AONBD则只需对滤波器参数进行优化，大大减少了计算量。

(2) 由于ASTFA采用了高斯牛顿迭代法，而高斯牛顿迭代法对初值的要求较高，如果初值选择不正确，往往不能正确的分解。而AONBD采用遗传算法对数据进行优化，随机产生初值，无需事先对初值进行设定。

(3) 仿真分析结果表明，相对ASTFA和EMD，AONBD在抑制端点效应和模态混淆、抗噪声性能、提高分量的正交性和准确性等方面具有一定的优越性，且AONBD的整体耗时要低于ASTFA。

将AONBD应用于转子系统碰摩振动信号的故障诊断，对其做包络谱分析后提取了信号的倍频、工频及分频成分，实现了转子的故障诊断，证明了该方法用于机械故障诊断的有效性。

值得一提的是，AONBD方法刚被提出，在算法的收敛性，迭代终止条件，优化算法和奇异局部线性算子等方面还需要进一步的探讨。随着这些问题的深入研究，AONBD方法拥有广阔的应用前景。

[1] Huang N E，Shen Z，Long S R. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society A，1998，454(1971): 903-995.

[2] Yeh J R，Shieh J S. Complementary ensemble empirical mode decomposition: A noise enhanced data analysis method[J]. Advances in Adaptive Data Analysis，2010，2(2): 135-156.

[3] Shen Z J，Chen X F，Zhang X L，et al. A novel intelligent gear fault diagnosis model based on EMD and multi-class TSVM[J]. Measurement，2012，45(1): 30-40.

[4] Thomas Y H，Shi Z Q. Adaptive data analysis via sparse time-frequency representation[J]. Advances in Adaptive Data Analysis，2011，3(1/2): 1-28.

[5] Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory，2006，52(4)：1289-1396.

[6] Yang H G，Mathew J，Ma L. Fault diagnosis of rolling element bearings using basis pursuit[J]. Mechanical Systems and Signal Processing，2005，19(2)：341-356.

[7] Mallat S，Zhang Z. Matching pursuit with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing，1993，41(12)：3397-3415.

[8] Frei M G，Osorio I. Intrinsic time-scale decomposition: Time-frequency-energy analysis and real-time filtering of non-stationary signals[J]. Proceedings of the Royal Society A，2007，463(2078): 321-342.

[9] Peng S L，Hwang W L. Adaptive signal decomposition based on local narrow band signals[J]. IEEE Transactions on Signal Processing，2008，56(7): 2659-2676.

[10] Xie Q，Li J P，Gao X G，et al. Fourier domain local narrow-band signal extraction algorithm and its application to real-time infrared gas detection[J]. Sensors and Actuators B: Chemical，2010，146(1): 35-39.

[11] 程军圣，郑近德，杨宇. 基于局部特征尺度分解的经验包络解调方法及其在机械故障诊断中的应用[J]. 机械工程学报，2012，48(19)：87-94.

CHENG Jun-sheng，ZHENG Jin-de，YANG Yu. Empirical envelope demodulation approach based on local characteristic-scale decomposition and its applications to mechanical fault diagnosis[J]. Journal of Mechanical Engineering，2012，48(19): 87-94.

[12] 罗洁思，于德介，彭富强. 基于多尺度线调频基信号稀疏分解的信号分离和瞬时频率估计[J]. 电子学报，2010，38(10)：2224-2228.

LUO Jie-si，YU De-jie，PENG Fu-qiang. Signal separation and instantaneous frequency estimation based on multi-scale chi rplet sparse signal decomposition[J]. ACTA Electronica SINICA，2010，38(10): 2224-2228.

[13] 楼梦麟， 黄天立. 正交化经验模式分解方法[J]. 同济大学学报:自然科学版，2007，35(3)：293-298.

LOU Meng-Lin，HUANG Tian-Li. Orthogonal empirical mode decomposition[J]. Journal of Tongji University:Natural Science，2007，35(3): 293-298.

[14] Yang Y，Cheng J S，Zhang K. An ensemble local means decomposition method and its application to local rub-impact fault diagnosis of the rotor systems[J]. Measurement，2012，45(3): 561-570.

[15] Lei Y G，Lin J，He Z J，et al. A review on empirical mode decomposition in fault diagnosis of rotating machinery[J]. Mechanical Systems and Signal Processing，2013，35(1/2): 108-126.

[16] 蔡艳平，李艾华，石林锁，等. 基于EMD与谱峭度的滚动轴承故障检测改进包络谱分析[J]. 振动与冲击，2001，30(2)：167-172.

CAI Yan-ping，LI Ai-hua，SHI Lin-suo，et al. Roller bearing fault detection using improved envelop spectrum analysis based on EMD and spectrum kurtosis[J]. Journal of Vibration and Shock，2001，30(2): 167-172.

[17] 韩捷，张瑞林. 旋转机械故障机理及诊断技术[M]. 北京：机械工业出版社，1997.

[18] 胡茑庆. 转子碰摩非线性行为与故障辨识的研究[D]. 长沙：国防科技大学，2001.

[19] 于德介，程军圣，杨宇. 机械故障诊断的Hilbert-Huang变换方法[M]. 北京：科学出版社，2006.

Adaptive optimization narrow-band decomposition method and its application

PENG Yanfeng, CHENG Junsheng, YANG Yu, LI Baoqing

(State Key Laboratory of Advanced Design and Manufacture for Vehicle Body,Hunan University, Changsha 410082, China)

The adaptive optimization narrow-band decomposition(AONBD) method was proposed. Signal decomposition was converted into optimizing parameters of a filter. The optimization objective was to obtain the optimal solution of signals. An original signal was adaptively decomposed into several intrinsic narrow-band components(INBC) via optimization. AONBD method had two steps. Firstly, the optimal filter was obtained with optimization. Secondly，the optimal solution was derived by filtering the original signal using the optimal filter. The basic theory and decomposition steps of AONBD were described. Comparisons were made among AONBD, the adaptive sparsest time-frequency analysis(ASTFA) and the empirical mode decomposition(EMD) by utilizing a simulated signal. The results showed that the AONBD method is superior to the other two methods in restraining end effects and mode mixing，anti-noise performance, and improving the orthogonality and accuracy of components. The AONBD method was applied to analyze vibration signals of a rotor. The results indicated that AONBD can be effectively applied to diagnose mechanical faults.

adaptive optimization narrow-band decomposition; intrinsic narrow-band components; local narrow-band signal; singular local linear operator; rotor fault diagnosis

国家科技支撑计划课题(2015BAF32B03);国家自然科学基金(51375152;51575168); 智能型新能源汽车国家2011协同创新中心、湖南省绿色汽车2011协同创新中心资助

2015-03-06修改稿收到日期：2015-08-08

彭延峰 男，博士生，1988年1月生

程军圣 男，博士，教授，博士生导师，1968年10月生

E-mail：signalp@tom.com

TH165.3; TN911.7

A

10.13465/j.cnki.jvs.2016.15.001