基于粒子群算法的越野车悬架参数优化

刘笃优，张新峰，王灵龙，张广玉LIU Du-you， ZHANG Xin-feng， WANG Ling-long， ZHANG Guang-yu（中国汽车技术研究中心，天津 300300）

基于粒子群算法的越野车悬架参数优化

刘笃优，张新峰，王灵龙，张广玉
LIU Du-you， ZHANG Xin-feng， WANG Ling-long， ZHANG Guang-yu
（中国汽车技术研究中心，天津 300300）

针对基于平顺性的悬架参数优化问题，建立了越野车后悬架系统参数优化的数学模型，包括优化变量、目标函数和约束条件，设计和应用了三种改进的粒子群算法，线性时变惯性权重粒子群算法、随机惯性权重粒子群算法和时变加速因子粒子群算法，来对车辆悬架平顺性进行优化，并与遗传算法对比。仿真结果表明，时变加速因子粒子群算法在收敛速度和收敛精度上都明显高于其他算法，优化后的车辆平顺性大大提高。

越野车；悬架；粒子群算法；参数优化

0　引言

越野车经常行驶在坑洼不平的路面上，悬架参数匹配的不合理就会很容易导致车身加速度、悬架动挠度以及轮胎动载荷增大，使车辆行驶平顺性和安全性恶化。车辆悬架系统是典型的多输入多输出系统，悬架参数与车辆平顺性评价指标不是简单的线性、一对一的关系，而是复杂的非线性、多对多的关系，一个悬架参数的改变就会影响多个平顺性指标的变化，可以说悬架系统是一个矛盾的集合体，存在严重的耦合现象。

粒子群算法（Particle swarm optimization，PSO）是Kennedy和Eberhart在1995年的IEEE国际神经网络学术会议上提出的群智能优化算法［1］。和遗传算法（Genetic algorithm，GA）等其他群优化算法一样，粒子群算法也是在搜索空间内随机初始化粒子，但和其他进化算法不同的是，粒子群算法在搜索过程中不存在个体之间遗传物质的直接重组，粒子群算法是基于种群中粒子的群体社会行为来进行优化。在每一次迭代中，粒子群算法通过简单地调节每个粒子朝向其自身历史最佳位置及朝向整个种群的最好粒子位置，来进行全局寻优。由于粒子群算法实现简单并且能够快速收敛到一个相当不错的解，所以其广泛用于求解复杂优化问题［2～4］。

本文以越野车后悬架刚度和阻尼为优化变量，以悬架动挠度、轮胎动载荷以及悬架刚度、阻尼范围为约束条件，以车身垂向加权加速度均方根值为优化目标，通过设计和运用三种改进的粒子群算法，线性时变惯性权重粒子群算法（PSO-TVIW）、随机惯性权重粒子群算法（PSO-RANDIW）和时变加速因子粒子群算法（PSO-TVAC），来对车辆悬架平顺性进行优化，通过与遗传算法对比表明，粒子群算法对求解悬架优化问题很有优势。

1　悬架系统参数优化的数学模型

1.1悬架系统振动模型

在建立后悬架二度振动模型之前，需要完成路激励的建模，参照GB/T 4970-2009车辆平顺性试验方法［5］，建立随机路面激励模型。

1.1.1路面激励模型

通过MATLAB/SIMULINK自带的限带白噪声模块，利用有理函数滤波白噪声生成法建立不同等级路面的时域模型［6，7］。车轮所受路面随机激励的时域数学模型如式（1）所示，得到的E级路面位移功率谱密度如图1所示。

式中：q（t）为路面不平度位移，v为车速，Gq（n0）为路面不平度8级分类标准中规定的不平度系数的几何平均值，w0（t）为均值为零的白噪声。

1.1.2悬架系统振动模型

考虑轮胎刚度和阻尼的悬架系统二自由度模型如图2所示，其中q为路面激励；z1为簧下质量垂向位移；z2为簧上质量垂向位移，m1为簧下质量，m2为簧上质量，k为悬架刚度，kt为轮胎刚度，c为悬架阻尼，ct为轮胎阻尼。

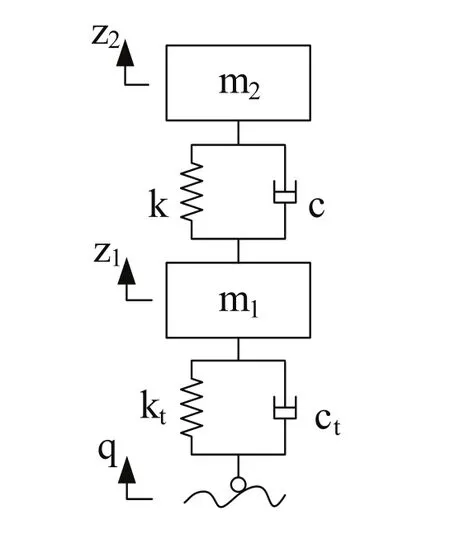
图2　后轴悬架振动模型

1.2目标函数

以悬架刚度和阻尼为优化变量，参照GB/T 4970-2009汽车平顺性试验方法，选择随机路面下车身垂向1/3倍频带加权加速度均方根值最小作为优化目标［5］。即：

1.3约束条件

1.3.1刚度约束

由悬架静挠度表达式：fs=m2g/k，根据越野车悬架静挠度的设计范围60mm～130mm［8］，故悬架刚度约束范围：

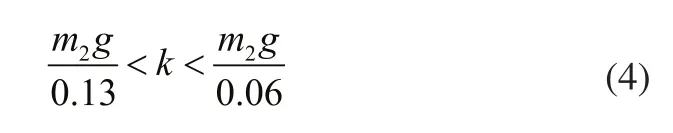
1.3.2阻尼约束

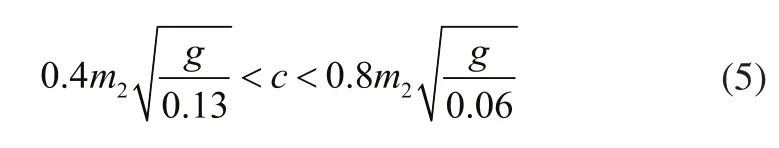
1.3.3动挠度约束

1.3.4相对动载荷约束

为兼顾汽车驱动性能、操作稳定性和行驶安全性，悬架相对动载荷均方根值一般满足：。

综上，可以得到不等式约束优化数学模型：

为了便于PSO求解，应用罚函数将不等式约束优化数学模型转化成无约束优化数学模型，如：

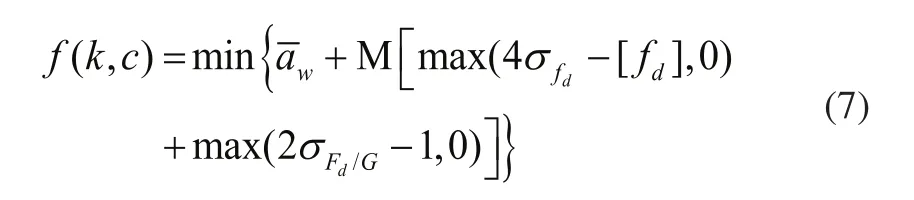
其中，M为足够大的正整数。

2　粒子群算法设计

在粒子群算法中，搜索空间中的每个粒子根据其自身的飞行经验和其他粒子的飞行经验，动态调整粒子速度，从而达到粒子轨迹的调整。每一个粒子的自身状态都由一组位置和速度向量描述，分别表示问题的可行解和它在搜索空间中的运动方向［9］。所以粒子群算法的速度和位置更新方程是粒子群算法的核心，如式（8）所示［10～12］：

其中，i表示第i个粒子，d表示粒子的第d维；vid（t）表示粒子i在进化到第t代时的第d维飞行速度分量；xid（t）表示粒子i进化到第t代时的第d维位置分量；pid（t）表示粒子i在进化到第t代时的个体最优位置pi的第d维分量；pgd（t）表示进化到第t代时整个粒子群的最优位置pg的第d维分量；w为惯性权重；c1为认知因子，c2为社会因子；r1、r2为［0，1］的随机数。

为了平衡全局搜索和局部搜索，Shi和Eberhart提出线性时变惯性权重粒子群算法（PSO-TVIW）［13］，即：

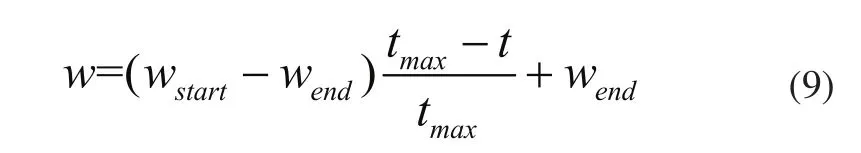
采用随机惯性权重粒子群算法（PSO-RANDIW）可以灵活调整全局搜索和局部搜索，保持种群多样性，在这种算法中，惯性权值如下式调整：

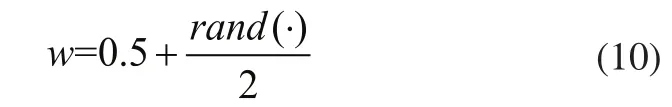
其中，rand（·）为［0，1］的随机数。

为了提高算法收敛性，Ratnaweera等提出时变加速因子粒子群算法（PSO-TVAC）［7］，在算法初期，增大认知部分，减小社会部分可以使个体在整个搜索空间遍历；算法后期，减小认知部分，增大社会部分可以使粒子收敛到全局最优。加速因子调整策略如下式所示：

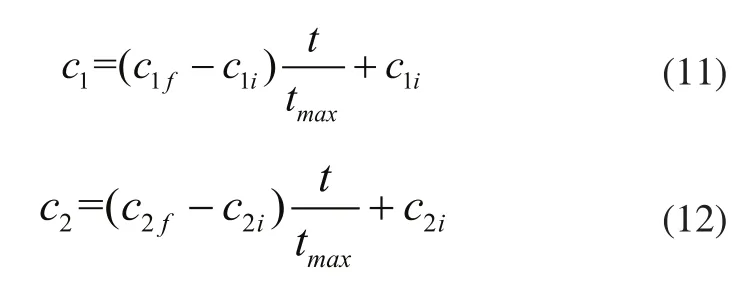
下面应用4个标准的8维测试函数对上述三种粒子群算法进行测试，来证明上述算法的有效性。标准测试函数参数如表1所示，粒子种群规模设置为30，迭代次数为200次，每种算法各运行50次，取其平均值作出最优适应值随迭代次数变化曲线，如图3所示。可以看出，PSO-TVAC收敛速度和收敛精度要明显好于其他两种算法，尤其对单峰值函数Sphere效果最为明显，其他两种算法，PSO-TVIW要好于PSO-RANDIW。

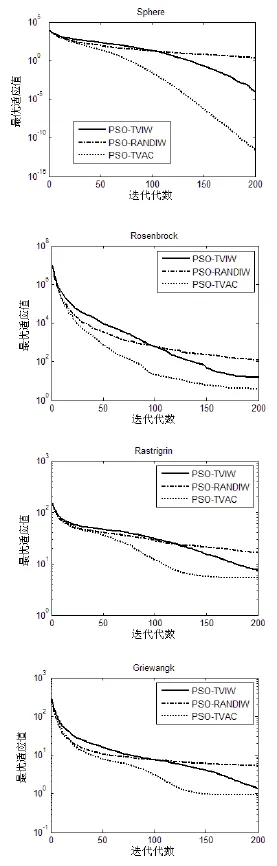
图3　测试函数最优适应值随迭代次数变化曲线

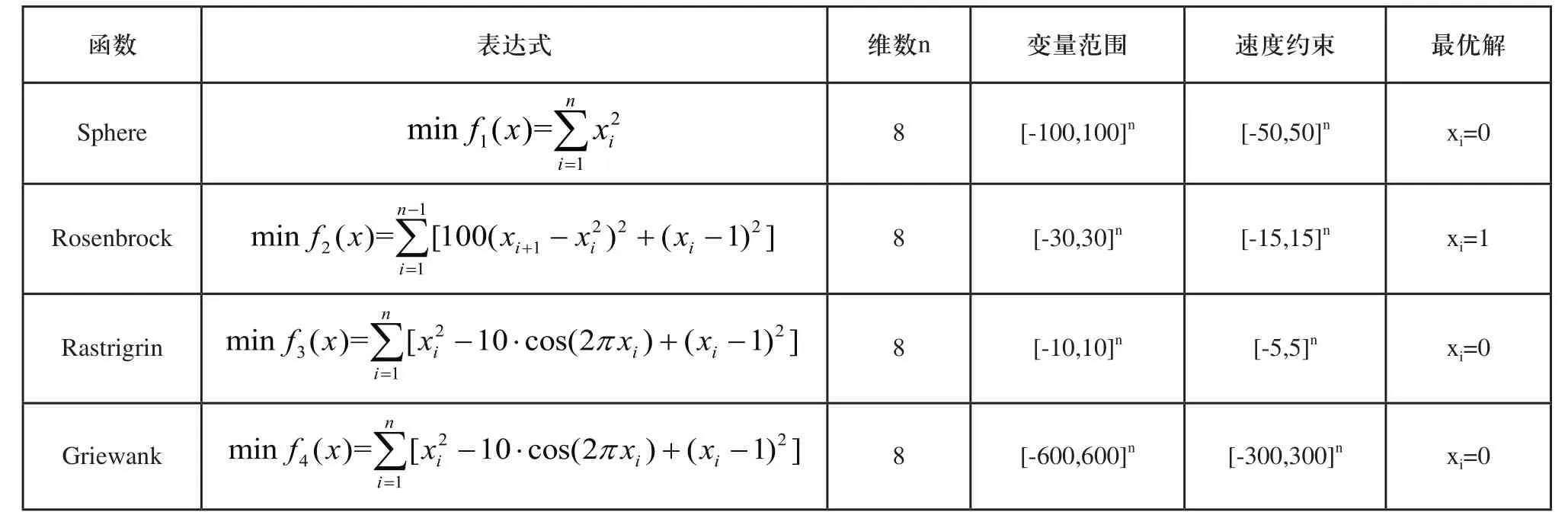
表1　标准测试函数参数

3　悬架参数优化

通过已经建立好悬架系统振动仿真模型，应用PSO-TVIW、PSO-RANDIW和PSO-TVAC三种粒子群算法对矿用车后悬架进行参数优化。图4是粒子群算法优化悬架参数数据流图，首先粒子群算法产生变量输入到悬架系统振动模型中，通过调用悬架仿真模型求出该变量下的适应值，再把适应值返回到粒子群算法中，通过适应值大小判断优化变量是否为最优解。

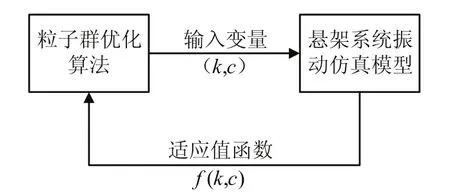
图4　粒子群算法优化悬架参数数据流图

粒子群算法需要限制每个维度的最大允许速度，以避免在预定义的搜索空间之外过度搜索，表2给出了优化变量动态搜索范围和速度约束范围。

表2　优化变量范围和速度范围

设置最大迭代代数为200代，种群规模为30，分别调用三种粒子群算法进行优化，可以得到最优适应值随迭代次数的变化趋势，如图5所示，通过这一趋势可以看出不同算法的性能差异。对比遗传算法（GA），可以看出所应用的三种粒子群算法都优于遗传算法，PSOTVAC在收敛速度和收敛精度都明显高于其他算法，PSO-TVIW次之，PSO-RANDIW最差，而遗传算法在设定的迭代代数内没有跳出局部最优解。表3是算法得到的优化设计参数，可以看出应用粒子群算法对越野车后悬架进行优化，可以大幅减小车身垂向加速度的均方根值，提高乘坐舒适性。

图5　最优适应值随迭代次数变化曲线

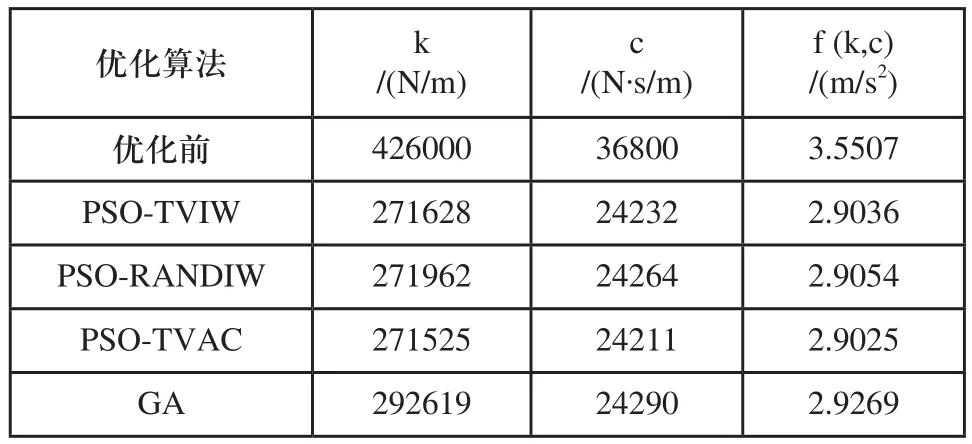
表3　算法得到的最优解

4　结论

粒子群算法在求解复杂优化问题上具有优势，将粒子群算法应用到求解悬架参数优化问题，可以看出，在算法收敛速度、收敛精度以及跳出局部最优能力方面，粒子群算法都比遗传算法要好。通过调整标准粒子群算法的惯性权重和加速因子，能够提高算法的收敛速度和收敛精度，在设定的迭代代数内使算法具有较高的求解效率，仿真计算结果表明，时变加速因子粒子群算法（PSO-TVAC）在收敛速度和收敛精度上都明显高于其他算法，可以应用到求解悬架更多参数的优化问题。

［1］ Kennedy J，Eberhart R.Particle swarm optimization［A］. Proceedings of IEEE inter--national conference on neural networks［C］.1995，4（2）：1942-1948.

［2］ Ioan Cristian Trelea. The particle swarm optimization algorithm convergence analysis and parameter selection［J］.Information Processing Letters，2003（85）：317-325.

［3］ Carlos A， Coello Coello. Handling multiple objectives with particle swarm optimization［J］. IEEE TRANSACTIONS ON EVOLUTIONARY COMPUTATION， 2004， 8（3）：256-279.

［4］ Maurice Clerc and James Kennedy. The particle swarm- explosion，stability and convergence in a multidimensional complex space［J］.IEEE TRANSACTIONS ON EVOLUTIONARY COMPUTATION，2002，6（1）：58-73.

［5］ 秦民，刘明辉.应国增，等.GB/T 4970-2009汽车平顺性试验方法［S］.北京：中国标准出版社，2010.

［6］ 吴志成，陈思忠，杨林，张斌.基于有理函数的路面不平度时域模型研究［J］.北京理工大学学报，2009，29（9）：795-798.

［7］ 檀润华，陈鹰，路甬祥.路面对汽车激励的时域模型建立及计算机仿真［J］.中国公路学报，1998，11（3）：96-102.

［8］ 余志生.汽车理论［M］.北京：机械工业出版社，2013.

［9］ 钱锋.粒子群算法及其工业应用［M］.北京：科学出版社，2013.

［10］ 刘玲，钟伟民，钱锋.改进的混沌粒子优化算法［J］.华东理工大学学报，2010，36（2）：267-272.

［11］ 崔航.基于粒子群算法的汽车平顺性参数优化［D］.吉林大学，2007.

［12］ 张弓.基于预决策粒子群算法的悬架仿真优化［D］.浙江大学，2011.

［13］ Shi Y， Eberhart R C.Empirical study of particle swarm optimization［A］.Evolutionary Computation，1999.CEC 99. Proceedings of the 1999 Congress on.IEEE［C］.1999，3.

［14］ Ratnaweera A，Halgamuge S，Watson H C. Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients［J］.Evolutionary Computation，IEEE Transactions on，2004，8（3）：240-255.

Parameters optimization for off-road vehicle suspension based on particle swarm algorithm

U461.4

A

1009-0134（2016）08-0091-05

2016-05-21

刘笃优（1990 -），男，江苏赣榆人，工程师，工学硕士，研究方向为汽车悬架优化设计。