基于ANSYS的爬壁机器人永磁吸附单元研究

薛 珊，冯志强，徐 龙，赵运来，吕琼莹XUE Shan， FENG Zhi-qiang， XU Long， ZHAO Yun-lai， LYU Qiong-ying（长春理工大学 机电工程学院，长春 130022）

基于ANSYS的爬壁机器人永磁吸附单元研究

薛 珊，冯志强，徐 龙，赵运来，吕琼莹
XUE Shan， FENG Zhi-qiang， XU Long， ZHAO Yun-lai， LYU Qiong-ying（长春理工大学 机电工程学院，长春 130022）

针对如何提高永磁式爬壁机器人磁吸附单元吸附能力，提出了一种新型的磁吸附单元模型。运用ANSYS中的ANSOFT Maxwell模块对吸附单元模型的二维静态磁场进行了仿真分析，通过分析磁吸附单元各结构尺寸对吸附力的影响，得出水平充磁的方型永磁体改变其高度尺寸对磁吸附力的影响大于改变水平磁化尺寸的影响。对比了传统型和新型单元在尺寸结构相同的条件下，吸附力随工作气隙变化的关系，结果表明新型的磁路具有永磁利用率高、吸附力大、吸附稳定性好等优点。

永磁式；爬壁机器人；ANSOFT Maxwell；磁吸单元

0　引言

爬壁机器人因其可攀爬垂直或者陡峭的壁面工作，在国外又被称为极限作业机器人。它可代替人类在高耸危险的壁面上工作，将人类从传统的人工劳动中解救出来，在保障人身安全的同时也能提高工作效率，因此长期以来都受到学者们的重视。根据吸附方式的不同分为负压吸附爬壁机器人和磁吸附爬壁机器人。磁吸附爬壁机器人应用较广泛的吸附装置主要有电磁铁、永磁铁、可变磁极永磁体三种。磁吸附式爬壁机器人具有吸附可靠、承载能力强等特点，非常适合于大型铁磁性结构件的攀爬［1］。

磁吸附单元是磁吸式爬壁机器人的主要核心组成部分，众多国内外学者对此进行了大量的研究。主要是通过改变磁路设计方式，从而提高磁利用率，使磁吸附单元的效率更高［2］。

本文设计了一种利用永磁体同名磁极相接的直线阵列结构，相比于传统的磁路，磁吸附能力有了显著地提高。将吸附单元镶嵌在履带式爬壁机器人的链条上，可提高其携带负载且克服钢铁壁面凹凸不平稳定前行的能力。

1　磁吸附单元的磁路设计

永磁体的磁路是指磁通量通过磁介质的路径，从永磁体内部发出的磁力线，经导磁能力强的轭铁引至需要磁力作用的工作间隙内，再通过导磁材料返回到永磁体，从而构成了一个闭合磁力线回路。合适的选择磁路的结构可以将磁体工作在永磁体最大磁能积点上［3］。使得工作气隙内的磁通密度增加，从而最大限度发挥永磁体的性能，保证爬壁机器人在钢铁壁面的吸附性能可靠，因此磁路的设计是永磁吸附单元设计的核心。磁路主要由永磁体、导磁轭铁和隔磁材料铜组成。如图1所示，其中箭头所指的方向即为永磁体充磁的方向，永磁材料形状选择方形的，以便于材料的加工和安装。

图1　新型磁路与传统磁路示意图

如图1（a）、图1（b）所示传统型和新型磁吸附单元磁路设计模型。传统型采用径向充磁方式，各永磁体之间由隔磁材料隔开通过上部的导磁材料引导磁力线的分布。新型单元采用轴向充磁方式，各永磁体间由导磁材料连接，上部使用隔磁材料，减少结构的漏磁。

为了更好的对比传统型和新型磁路磁力线及磁感应强度分布情况。运用ANSOFT Maxwell模块分别对两种磁路按照相同结构尺寸进行建模分析。

图2　两种磁路磁感应及磁力线分布情况

如图2（b）所示，新型磁路顶部的隔磁材料有效的减少了磁力线向空气中漏磁。中间导磁率高的轭铁作用是将永磁体磁力线由水平方向改变成垂直方向并将其引至工作气隙中，同时若无轭铁磁极相对的磁体需要借助很大的外力作用才能保证磁体间安装间隙极小，避免漏磁，安装时先将两块轭铁吸附至中间磁体上，再安装两侧磁体。两侧的导磁铁减少了端部的漏磁，具有聚磁效应，将磁力线引向钢铁壁面，有助于提高单元的磁吸附力。此设计结构采用了内、外磁式相结合的方式［4］，充分利用了它们各自的优点。一方面，通过阵列的顶侧的隔磁材料、中间及两侧的轭铁所形成内磁式结构，减少了漏磁的磁通量，高效利用了永磁体的磁力线。另一方面，工作侧的永磁体和钢铁壁面接触作为主要吸附面，形成外磁式结构，增强了有效工作气隙磁通，减少了传统永磁吸附单元所需的磁轭。

对比图2（a）、图2（b）中两种磁路的磁感应强度及磁力线分布。产生的最大磁感应强度传统型的为1.78T，新型的为1.82T。虽然两者相差不大，但是传统型磁路磁力线经过上部的轭铁产生聚磁，因此为避免磁饱和现象其对轭铁的需求较多，而新型的最大磁感应强度主要集中工作间隙内，因此所需轭铁少，减少了磁损，永磁利用率高。对比磁感应强度分布情况。新型磁路在钢铁壁面内产生的磁感应强度比传统型的分布均匀、影响范围深。因此新型磁路更适应由于钢铁表面凹凸不平而引起的工作气隙变化。

2　永磁单元磁吸力计算

按力学原理：一体系在某一方向的力或力矩等于该体系下的能量在这一方向的梯度。对于永磁体来说：体系能量=气隙能量=气隙体积×单位体积的磁能［5］，即为：其中Lg为永磁与导磁壁面的间隙，Sg为气隙面积，Bg为气隙内的磁密，μ0为空气的磁导率。在Lg方向上的力为：

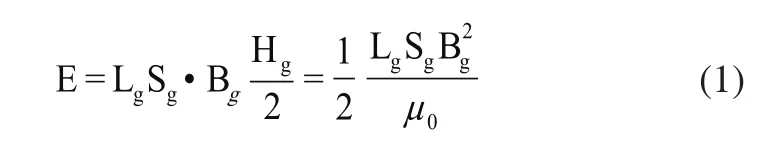
假设工作气隙Lg较小，将永磁吸附单元与壁面之见的气隙分为n等份，根据永磁吸附单元所产生的吸附力公式，可将式（2）改写成［6］：

其中Bi为单个网格内的磁感应强度，S为工作气隙的总面积，α为磁吸单元与壁面的夹角。

根据磁通连续原理和安倍环路定律，考虑磁路中存在漏磁，可求出气隙磁感应强度为［5］：

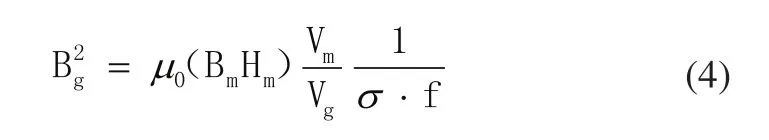
其中Vm=SmLm为永磁体体积，Vg=SgLg为工作间隙体积。σ为漏磁系数，不同的磁路结构的数值差别很大。f为磁路的磁阻系数（磁势损失系数）一般在1.05～1.45。由式（2）和式（4）可得：

由式（2）可知，空气的磁导率是不变的，气隙中磁感应强度Bg及有效气隙面积Sg对吸附力F具有重要影响。由式（4）可知，影响Bg的主要因素有永磁体体积Vm、间隙体积Vg、漏磁系数σ、磁阻系数f、磁能积（BmHm），它们的值都受结构尺寸的影响。由式（5）可知，吸附力F随磁体体积Vm的增加而增大，随气隙Lg的增大而降低。因此改变永磁体结构参数及工作气隙间隙，可改善吸附力的大小。

3　有限元建模仿真及结构参数优化

3.1建立有限元模型和定义材料

有限元分析软件ANSYS中的ANSOFT Maxwell模块可进行二维或三维的电磁场分析。本文分析的永磁吸附单元可以认为在z方向上无限延伸，即可将其磁场看做为二维静态磁场进行分析［7］。

图3　二维有限元结构模型

建立如图3所示的二维有限元模型，其中永磁体及导磁轭铁的尺寸为T=4mm，A=B=H=10mm，D=4mm。

吸附单元静态磁场分析涉及的材料有永磁体、轭铁、吸附壁面、隔磁材料以及气隙介质。采用Maxwell软件材料库自带的永磁材料钕铁硼牌号为35（NdFeBN35），其磁性能参数如表1所示［8］。仿真过程中永磁材料的相对磁导率μr=1.0997785。

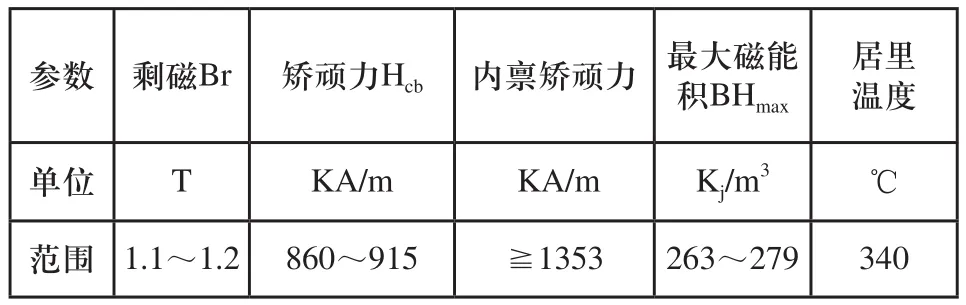
表1　钕铁硼N35参数

导磁轭铁和工作壁面均采用钢铁（steel-1008），考虑其材料的B-H为非线性的。其磁感应强度随磁场强度的增大迅速上升，随后增速放缓［9］。

工作气隙介质选择空气，μr=1.0。

隔磁材料选择铜，其相对磁导率μr小于1。

3.2结构参数对吸附力的影响分析

由式（2）和式（4）可知，永磁体的截面积Sm和长度Lm，结构中间和两侧导磁轭铁的截面积都会影响到有效工作磁气隙的截面积Sg，以及气隙Lg的大小，均会对气隙中的磁场强度产生影响，从而影响吸附力的大小。为了研究结构参数对吸附力的影响，取永磁体及导磁轭铁均为10mm×10mm的正方形，两侧轭铁宽4mm，隔磁材料厚度为4mm。

3.2.1永磁体磁化长度A对吸附力的影响

在ANSOFT Maxwell的二维磁场模型中，取B=H=10mm，D=T=4mm。建立优化扫描参数变量A，其值范围10mm～20mm，等间隔1mm。分析后在结果绘图中查看吸附力随磁化长度A的变化曲线。

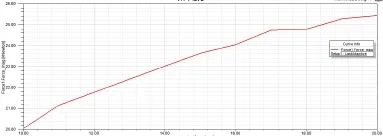
图4　磁化长度A对吸附力的影响

如图4所示随着磁化长度的增加吸附力先随之增大后趋于平缓。永磁体体积增大了一倍，磁吸附力由20.05kN增加到25.45kN，只提高了27%，说明永磁体的利用率不高。原因是由于随着磁体长度增大，磁力线主要经过磁导率大的轭铁，穿过气隙、壁面形成闭合回路。在磁体中间部分气隙内的磁感应强度减弱，气隙磁感应强度分布不均匀性增加。同时磁体体积增大磁通量增加，导磁轭铁与壁面间的气隙磁通逐渐接近饱和状态，导致气隙磁感应强度不再增加。当达到16mm～18mm之后时吸附力的增长趋于平缓，此时再增加磁体磁化长度对改善吸附力的作用已经很小了。综合考虑，永磁体磁化长度在满足吸附要求的条件下，不应选择过长。也就是说磁体长度与导磁轭铁长度的比值即A/B应在1.4～1.6的范围内较为合理。

3.2.2永磁体高度H对吸附力的影响

同理取A=B=10mm，T=D=4mm。新建优化扫描参数变量H，其范围为10mm～25mm，等间隔1mm。在结果绘图中查看吸附力随永磁体高度H的变化曲线。

图5　磁体高度H对吸附力的影响

如图5所示吸附力随着磁体高度的增加而单调增加。高度H由10mm增至20mm永磁体体积增大一倍，吸附力由20.05kN增加至47.03kN，增加了135%。这表明永磁体的利用率提高了。在H<24mm时增速较快，原因是磁体积增大气隙内的磁感应强度随之增大。当H>24mm时，吸附力增值速度减缓，是因为气隙磁通逐渐趋近饱和。综合考虑磁体的高度H与磁体磁化长度A的相对比值不应过大，H约为A的二倍，即取值区间为20mm～24mm时磁吸附力与磁利用率较好。

对比图4和图5中磁化方向长度A和磁体高度H对吸附力的影响，等体积的永磁体磁体高度对吸附力的影响大于磁化长度。例如在其他条件都相同时永磁体H=20mm，A=10mm是H=10mm，A=20mm时吸附力的值的1.9倍。

3.2.3两侧导磁轭铁厚度T对吸附力的影响

同理取A=H=B=10mm，D=4mm，新建优化扫描参数变量T范围为1mm～7mm，等间隔1mm。在结果绘图中查看吸附力随导磁轭铁厚度T的变化曲线。

图6　两侧导磁轭铁对吸附力的影响

如图6所示，随着T的增加，吸附力先上升后基本上保持不变。T为1mm吸附力为18.13kN，T为4mm时吸附力为20.05kN。主要是因为T值过小时，两侧轭铁的磁通量达到磁饱和，经轭铁向外部的漏磁增加，减少了与端部轭铁和气隙构成的磁力线回路，气隙中磁通量减少；随着T的继续增加，漏磁逐渐减少，气隙中磁通量增加，吸附力随之增大。当T>4mm时，磁通量基本不变，T对吸附力的影响减弱。因此两侧轭铁长度T取4mm为宜。

3.2.4气隙长度Lg对吸附力的影响

由于钢铁壁面存在凹凸不平的情况，吸附单元不能保证始终与壁面的间隙是保持不变的，因此需要测试气隙对吸附力的影响。

如图7所示为新型磁吸单元与传统型磁路气隙长度变化与吸附力关系，气隙Lg取值为1mm～9mm。由图可知，在间隙Lg为1mm时新型磁路的磁吸力比传统型的大一倍。虽然随着气隙的增大两者吸附力之差逐渐减小，但相同间隙情况下新型磁吸单元的吸附力始终远大于传统型。说明工作间隙越小新型磁路吸附力大的优势越明显，且吸附可靠性更高、适应能力强。

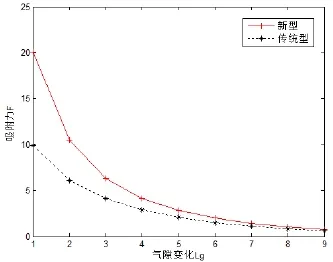
图7　气隙变化对吸附力的影响

4　结论

1）为了提高爬壁机器人的吸附能力，设计的永磁体磁极同名相对的吸附单元，相比同尺寸传统型磁路单元的吸附力有显著提高。

2）运用ANSYS中的ANSOFT Maxwell模块进行仿真分析，得到了水平充磁的方型永磁体，磁体高度方向变化对吸附力影响较大，当永磁体高度H为磁化长度A的二倍，水平磁化长度为轭铁水平长度1.5倍时，其吸附力大永磁利用率高，磁吸附性能好。为设计爬壁机器人的吸附单元提供了依据。

［1］ 刘枫.风力发电机塔身清洗机器人设计与研究［D］.黑龙江.哈尔滨工业大学，2013，7：1-2.

［2］ 钟华，白武帅，侯志坚，董军.通过永磁体同极相对提高磁场强度的研究［J］.中国现代教育装备，2014，187（3）：67-69.

［3］ 沈青青，张晋，李根.基于Halbach阵列爬壁机器人磁吸附单元的优化设计［J］.轻工机械，2014，32（5）：18-22.

［4］ 陈勇.Halbach阵列机器人磁吸附单元理论分析与实验研究［D］.江苏：南京理工大学，2013，11.

［5］ 钟文定，等.技术磁学（下册）［M］.科技出版社，2009，620-624.

［6］ 陈勇，昌明，包建东.新型爬壁机器人磁吸附单元优化设计［J］.兵工学报，2012，33（2）：1539-1544.

［7］ 赵剑坤，叶家玮.基于有限元分析的永磁吸附单元设计优化［J］.机械设计与制造，2009，47（3）：47-49.

［8］ 王军波，陈强，孙振国.爬壁机器人变磁力吸附单元的优化设计［J］.清华大学学报，2003，43（2）：214-217.

［9］ 潘柏松，张晋，魏凯，叶宇峰.基于Halbach阵列爬壁机器人永磁轮吸附单元的设计与优化［J］.浙江工业大学学报，2015，43（4）：393-396.

study on permanent-magnetic adhesion element of wall-climbing robot based on ANsYs

TH12

A

1009-0134（2016）08-0022-04

2016-06-03

吉林省科技发展计划项目（20126017）

薛珊（1978 -），女，副教授，博士，主要从事结构设计与分析研究。