新型矫直机矫直辊系模态分析

徐贺伟，卢秀春，杨荣刚XU He-wei， LU Xiu-chun， YANG Rong-gang（燕山大学 机械工程学院，秦皇岛 066004）

新型矫直机矫直辊系模态分析

徐贺伟，卢秀春，杨荣刚
XU He-wei， LU Xiu-chun， YANG Rong-gang
（燕山大学 机械工程学院，秦皇岛 066004）

为了解新型矫直机矫直辊系的动态特性，建立矫直辊系的动力学模型，并对理论计算进行仿真验证。在对压辊施加一定压下量、上主动辊施加一定预紧力条件下，推导构件动力学微分方程，计算固有频率，用ANSYS Workbench对辊系进行模态分析，得到辊系各阶阵型，将固有频率转化为线频率与模态频率进行对比，分析参数对模态频率的影响。结果表明：有限元仿真分析能够有效的反映矫直辊系动态特性，计算得到的频率与模态频率相对误差均在5%以内，模态仿真验证了理论推导的合理性，增大钢筋直径、减小压辊厚度和直径、增大矫直辊厚度均能增加辊系模态频率，钢筋直径、矫直辊厚度对辊系模态频率影响较大。研究结果为新型矫直机矫直辊系结构的优化提供了理论支持。

动态特性；新型矫直机；矫直辊系；模态分析

0　引言

生产刀具所用短圆柱合金钢一般由长直棒料或盘料供货的钢筋首先经过矫直，然后通过剪切机剪切钢筋获得所需长度的短圆柱合金钢。剪切过程会对矫直后的棒料直线度产生一定的影响。此外，随着建筑、铁路等行业的发展，工业生产对钢筋直线度提出了较高的要求。因此，需要精密矫直机对剪切后的短圆柱合金钢进行精密矫直。

新型矫直机能够实现对短圆柱合金钢的精密矫直，较多科研工作者对其进行了研究。近年来矫直技术发展迅速，矫直设备矫直质量提高，控制检测系统性能得到改善［1～3］。文献［4］设计了一种新型管材矫直机，对矫直机矫直后管材的椭圆度、直线度、残余应力进行了分析，并验证了新型矫直机设计的合理性；文献［5］对精密矫直机的辊系受力情况进行了分析，并用MATLAB编程、ADAMS仿真验证了矫直辊系设计的合理性，为矫直机的进一步优化提供理论依据；文献［6］研究了十五辊矫直机的矫直模型，验证了板材在十五辊组合矫直机中矫直可以达到较高的矫直精度。

本文研究一种新型全自动精密矫直机，矫直机可以实现自动上料、夹紧、检测钢筋挠度、下料等工作。在对压辊施加一定压下量、上主动辊施加一定预紧力条件下，建立矫直辊系动力学微分方程，计算了辊系固有频率，用ANSYS Workbench对矫直辊系各阶模态和辊系阵型进行了分析，并研究了各参数对矫直辊系模态频率的影响规律。研究结果为矫直机工作时主动辊的转速设置及矫直机辊系的优化设计提供理论依据，避免矫直时辊系振动对矫直精度的影响。

1　辊系结构组成及工作原理

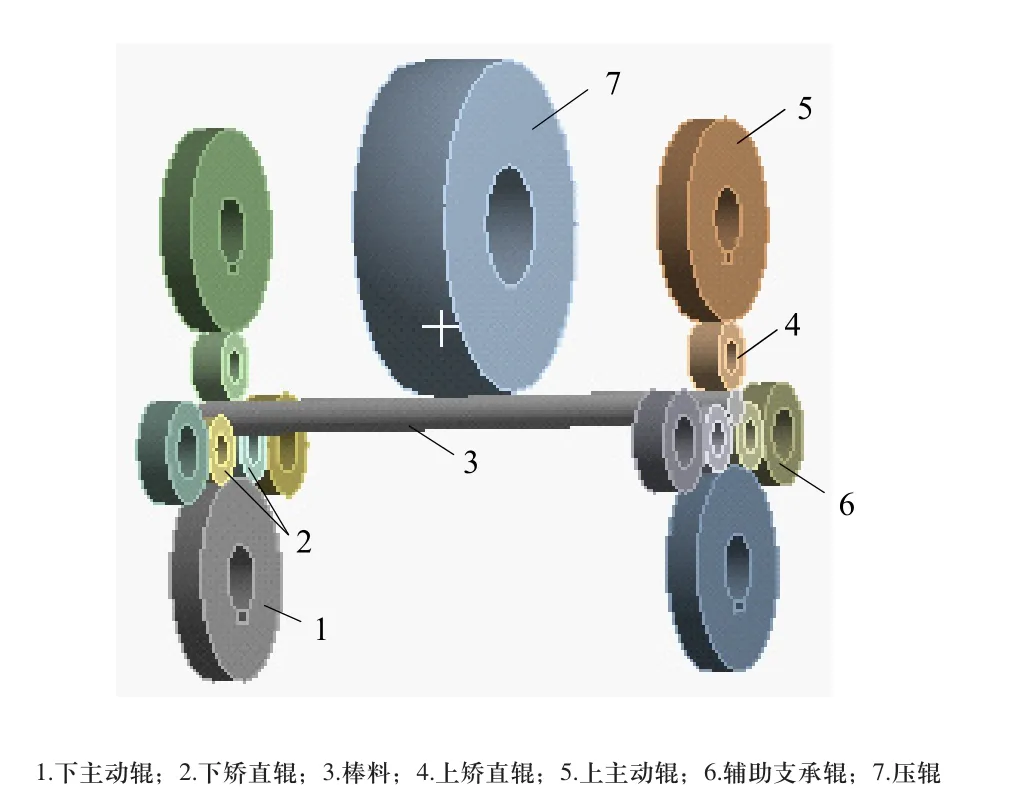
图1　辊系结构图

新型矫直机矫直辊系由十五辊组成，分别为压辊和左、右辊系，矫直机辊系结构图如图1所示。辊系由主动辊、矫直辊、辅助辊组成，电机带动主动辊旋转，主动辊通过摩擦带动上、下矫直辊旋转，左右矫直辊通过摩擦带动钢筋旋转，矫直过程是在钢筋旋转过程中进行。矫直辊系左右对称安装，辅助辊、矫直辊中心平行，上主动辊、上矫直辊采用浮动安装，实现矫直辊系对不同直径钢筋的夹紧作用，压辊可以左右移动，实现对棒料不同弯曲点的矫直，同时压辊的上下移动改变对矫直钢筋的压下量，经过几次接触后，减小钢筋的残余曲率，达到矫直的目的。

2　动力学模型建立

2.1动力学模型

新型精密矫直机的矫直辊系在动力学分析中作以下假设：

1）各辊只受辊系间压力的影响；

2）压辊下压δ后固定，压辊与短圆柱合金钢之间的接触力为正弦力；

3）矫直辊系各辊及短圆柱合金钢简化为刚体，各啮合处简化为线性弹簧；

4）辅助支撑辊与下主动辊固定。

在短圆柱合金钢端面所在平面建立直角坐标系xOy，考虑矫直辊、棒料、上主动辊的平移自由度，建立动力学模型如图2所示。矫直辊系的上主动辊、上矫直辊、棒料具有平移自由度，左、右两侧上主动辊自由度分别为yz5、yr5，左、右两侧上矫直辊自由度分别为yz4、yr4，棒料自由度为yz3，四个下矫直辊自由度分别为yzz2、xzz2、yzr2、xzr2、yrz2、xrz2、yrr2、xrr2。

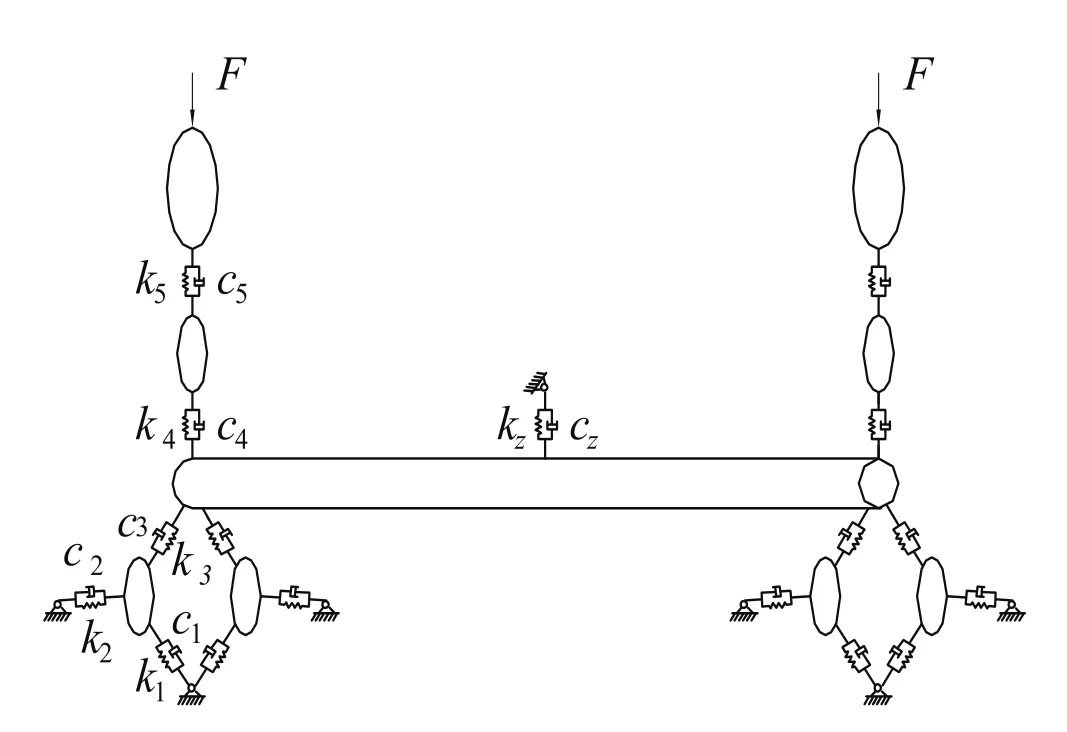
图2　动力学模型

2.2各构件动力学微分方程

将短圆柱合金钢安装在矫直辊上，压辊与钢棒恰好接触。对上主动辊施加预紧力F，并将压辊向下微移动δ后固定，根据各辊之间相对位移关系，利用牛顿第二定律建立精密矫直机辊系各构件动力学微分方程，微分方程为：

式中：

θ3为下矫直辊与棒料接触线法平面与y轴夹角；

θ2为下矫直辊与下主动辊接触线法平面与x轴夹角。

3　有限元模态分析

3.1有限元模态频率与阵型

辊系尺寸参数参如表1所示。

通过SolidWorks软件建立矫直辊系三维实体模型，将模型导入到ANSYS Workbench中，将矫直辊、压辊及辅助辊设置成结构钢材料，待矫钢棒设置成合金工具钢，对矫直辊系进行网格划分，该模型共有单元数2031，节点数共有12635，进行有限元模态分析［7～10］，得到辊系各阶模态频率。

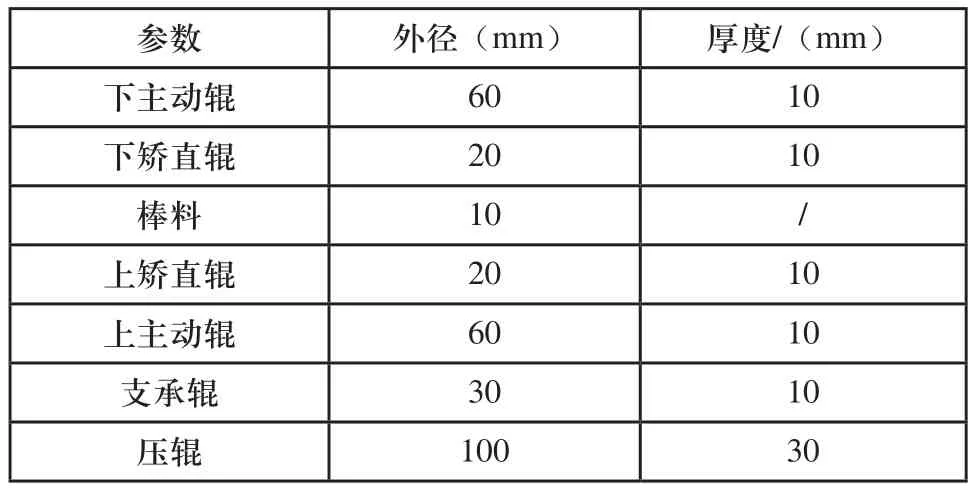
表1　尺寸参数

对矫直辊系进行模态分析，低阶模态阵型决定矫直辊系的动态振动特性，低阶频率更容易激励引起总成振动，Workbench分析中提取了矫直辊系前13阶模态频率，并对振型进行了分析，结果如表2所示。图3提取了模态阵型变化比较大的2、3、6、12阶模态阵型图。

固有频率与模态频率对比如表2所示，第5阶频率误差最小，误差值为1.19%，第12阶频率误差最大，误差值为4.58%，各阶频率误差均在5%以下，模态仿真验证了理论推导的合理性。

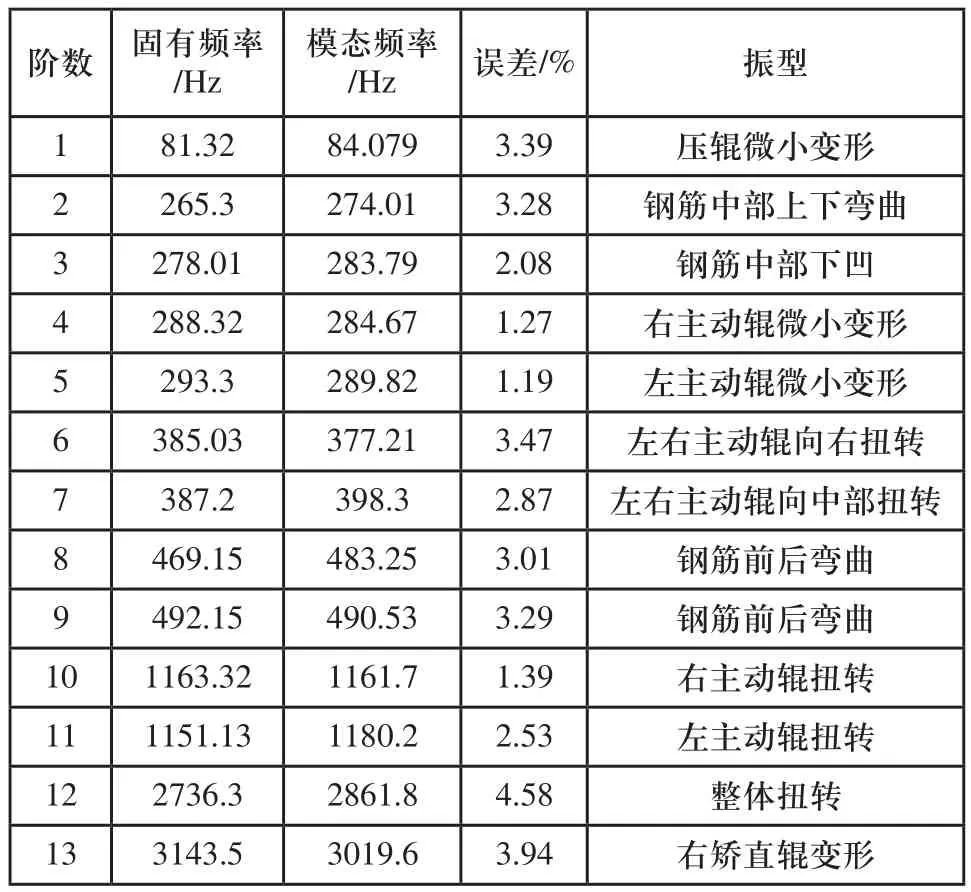
表2　模态频率与模态阵型

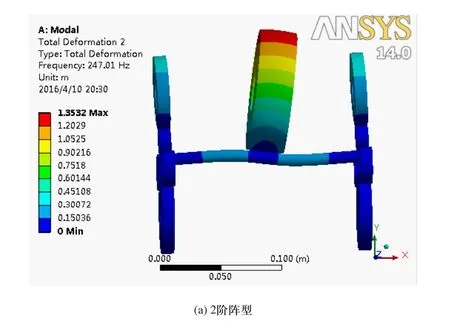
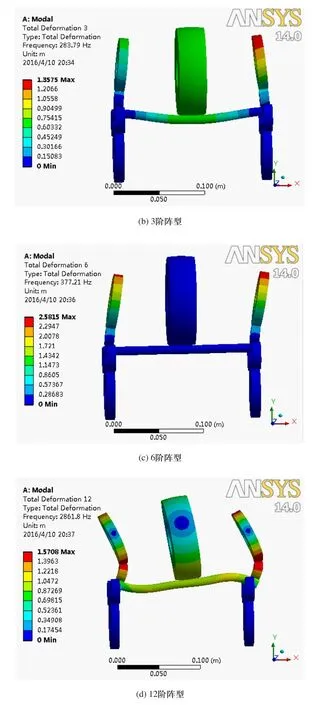
图3　辊系模态阵型图

由图3模态阵型图可知，第2阶模态频率导致钢筋弯曲，影响精密矫直机对钢筋最大挠度点的判断，对矫直精度有一定影响；第3阶模态频率导致钢筋中部下凹，左、右主动辊扭转，对矫直质量产生影响；第6阶模态频率主动辊同侧扭转，影响辊系之间的摩擦传动；第12阶模态频率对钢筋、主动辊、压辊变形影响较大，钢筋弯曲、主动辊和压辊扭转，导致矫直精度降低。

3.2参数对模态频率的影响分析

改变矫直辊系结构参数值，分析各参数对2、3、6、12阶模态频率的影响。选取短圆柱合金钢直径Φ1、压辊厚度hy、压辊直径Φ2、矫直辊厚度h作为变化参数，分析参数变化对模态频率变化的影响。

钢筋直径Φ1的变化对模态频率影响如图4所示。Φ1小于9.5及大于11时，ω2曲线斜率发生较大变化；Φ1小于10及大于11时，ω3曲线斜率发生较大变化；随着钢筋直径Φ1的增加，ω6曲线斜率先减小后增大，ω12曲线斜率逐渐减小。

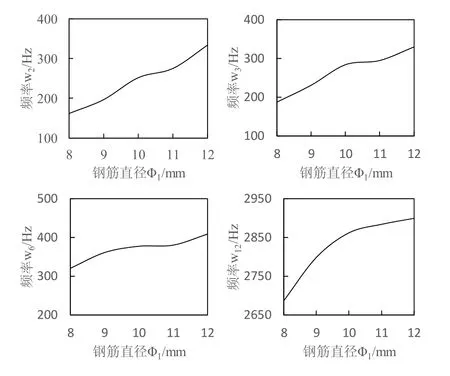
图4　Φ1对模态频率的影响

压辊厚度hy的变化对模态频率影响如图5所示。模态频率ω2、ω3、ω12值随着压辊厚度增加而减小，ω2曲线斜率发生微小变化，ω3曲线斜率逐渐增大，ω12曲线斜率逐渐减小；ω6随着压辊厚度的增加不发生变化。

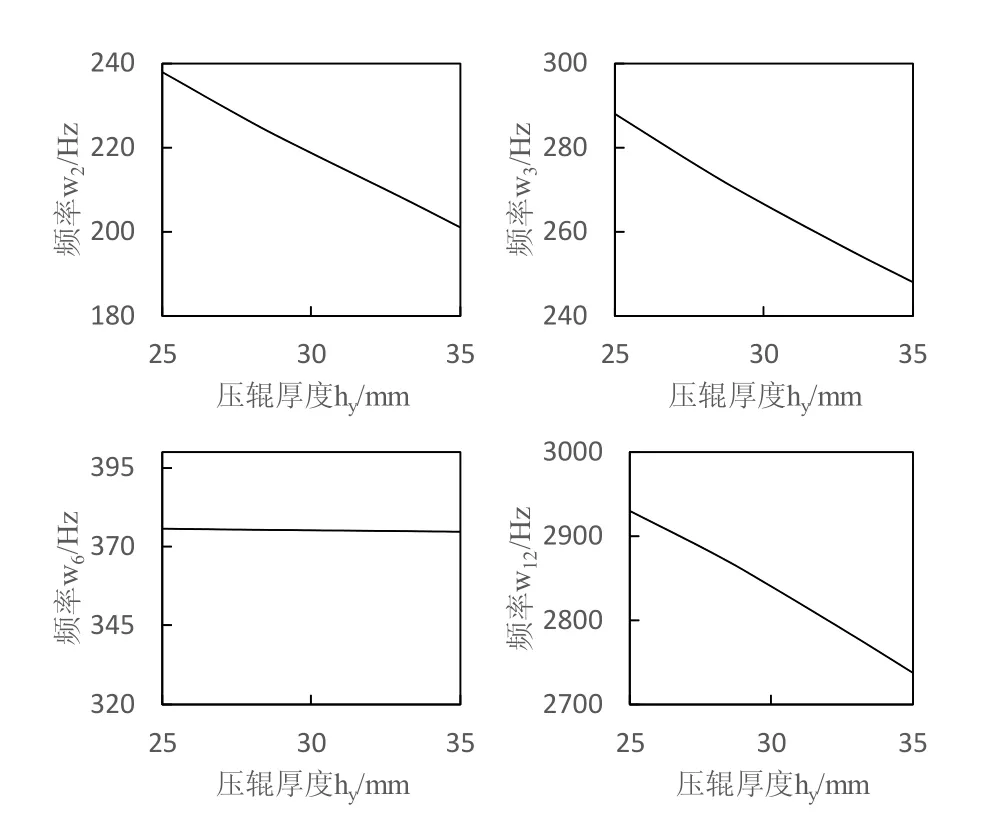
图5　hy对模态频率的影响

压辊直径Φ2的变化对模态频率影响如图6所示，模态频率ω2、ω3、ω6、ω12值随着压辊直径增加而减小，ω2与ω3曲线斜率先减小后增加；Φ2小于90mm和大于110mm时，ω6曲线斜率发生较大变化；Φ2小于90mm时ω12曲线斜率逐渐减小，Φ2等于90mm时ω12曲线斜率为零，Φ2大于90mm时ω12曲线斜率逐渐增大。

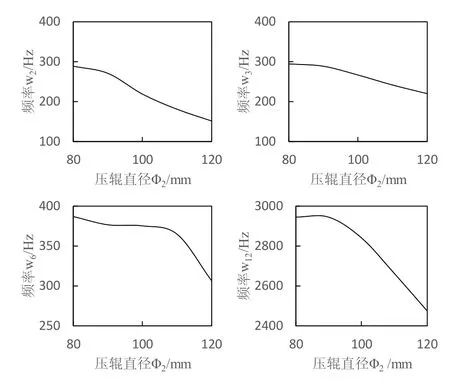
图6　Φ2对模态频率的影响

矫直辊厚度h的变化对模态频率影响如图7所示。模态频率ω2、ω3、ω6、ω12值随着矫直辊厚度增加而增大，ω2、ω3、ω12曲线斜率先减小后增大。h小于9.5mm和大于11mm时，ω6曲线斜率逐渐增大；h大于9.5mm和小于11mm时，ω6曲线斜率逐渐减小。

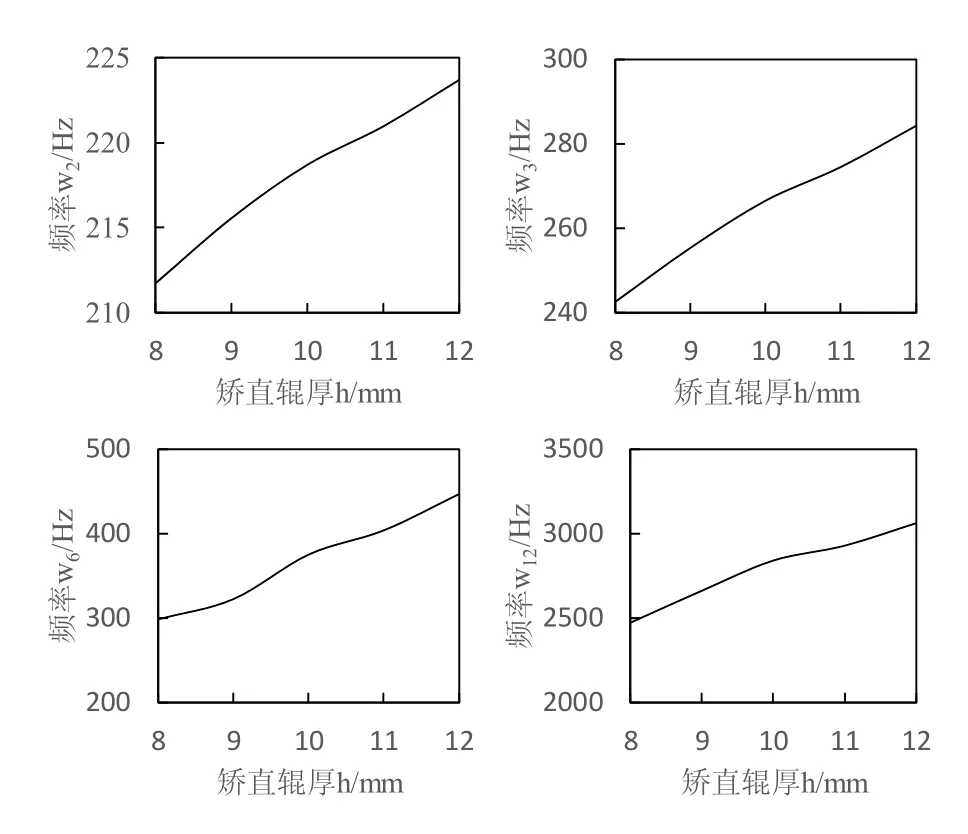
图7　h对模态频率的影响

4　结论

在对上主动辊施加预紧力F、压辊向下微移动δ条件下，建立动力学模型，推导动力学微分方程，对理论计算进行仿真验证，并进行参数分析。结果表明：

1）计算频率与仿真频率相对误差较小，模态仿真验证了计算结果的准确性，理论计算较全面的揭示新型矫直机的模态特性。

2）增加钢筋直径，模态频率ω2、ω3、ω6、ω12值增加；增加压辊厚度，模态频率ω2、ω3、ω12值减小，ω6保持不变；增加压辊直径，模态频率ω2、ω3、ω6、ω12值减小；增加矫直辊厚度，模态频率ω2、ω3、ω6、ω12值增大。模态频率随参数的变化规律为矫直机工作时主动辊的转速设置提供参考。

3）增加钢筋直径、减小压辊厚度及直径、增加矫直辊厚度，可以避免辊系振动对矫直机的影响。研究结果为全自动矫直机矫直辊系结构设计提供理论参考。

［1］ 卢秀春，金贺荣.数控带肋钢筋矫直切断技术［J］.建筑机械化，2000（4）：24-25.

［2］ 李双顶.矫直机定位系统的开发与设计［D］.重庆：重庆大学，2011.

［3］ 卢秀春，金贺荣，宜亚丽.热轧带肋钢筋矫直切断机的研究设计［J］.钢铁，2001，37（3）：59-62.

［4］ 许石民，王春迪，王京，等.超细管材矫直机设计及矫直动态仿真分析［J］.锻压技术，2016，41（2）：91-97.

［5］ 刘金，卢秀春，张玮.短钢棒矫直机矫直辊系受力分析与仿真［J］.塑性工程学报，2015，22（6）：78-83.

［6］ 王效岗，黄庆学，马勤.十五辊组合矫直机矫直模型研究［J］.四川大学学报：工程科学版，2008（6）.

［7］ 丁欣硕，凌桂龙.Ansys Workbench14.5有限元分析案例详解［M］.北京：清华大学出版社，2014：172-196.

［8］ 于天彪，王学智，关鹏，等.超高速磨削机床主轴系统模态分析［J］.机械工程学报，2012，48（17）：183-188.

［9］ 蔡力钢，马仕明，赵永胜，等.多约束状态下重载机械式主轴有限元建模及模态分析［J］.机械工程学报，2012，48（3）：165-173.

［10］ 马天飞，林逸，张建伟.轿车车室声固耦合系统的模态分析［J］.机械工程学报，2005，41（7）：225-230.

Modal analysis on straightening roll system of new-type straightening machine

TG333.2+3

A

1009-0134（2016）08-0026-04

2016-06-13

徐贺伟（1990 -），女，黑龙江人，硕士研究生，研究方向为矫直原理及矫直设备。