线驱动混合关节机器人构型与运动控制分析研究

李亚锋，赵江海，章小建，薛 峰LI Ya-feng， ZHAO Jiang-hai， ZHANG Xiao-jian， XUE Feng（1.合肥工业大学 电气工程与自动化学院，合肥 0000；.中国科学院合肥物质科学研究院 先进制造技术研究所，常州 1164；.莱克电气股份有限公司，苏州 15009）

线驱动混合关节机器人构型与运动控制分析研究

李亚锋1，2，赵江海2，章小建2，薛 峰3
LI Ya-feng1，2， ZHAO Jiang-hai2， ZHANG Xiao-jian2， XUE Feng3
（1.合肥工业大学 电气工程与自动化学院，合肥 230000；2.中国科学院合肥物质科学研究院 先进制造技术研究所，常州 213164；3.莱克电气股份有限公司，苏州 215009）

为提高工业机械臂的运动灵活性和避障能力，提出了一种由刚性旋转关节与连续型柔性关节构成的新型混合关节机器人，该机器人的关节轴线互相垂直并采用绳索驱动方式。首先，针对该混合关节机构，基于传统D-H参数法与弹性体常曲率变形理论提出了线驱动混合关节机器人运动学建模新方法。其次，在机器人建模分析的基础上，设计其运动控制系统，制备了原理样机。最后，开展原理样机实验，运动轨迹最大误差为10mm，实验结果验证了该混合关节机器人机构设计与运动控制的可行性。

线驱动；混合关节；运动学；控制系统

0　引言

1999年，英国机器人学者Robinson等提出了离散、蜿蜒和连续型机器人的分类概念［1］。传统的工业机器人可归为离散型机器人，一般由5～7个刚性关节和连杆构成，适用于结构化空间作业。蛇形机器人作为蜿蜒型的典型代表，由数量众多的刚性关节和短连杆构成，具有很高的灵活性［2］。而连续型机器人由单段或多段弹性体构成，依靠弹性体弯曲变形产生运动，类似于大象鼻子、章鱼触手和哺乳类动物的舌头等动物器官。

2007年，Choi等人研制了一种基于弹簧骨架的连续型内窥镜机器人［3］，该机器人内部关节间通过弹簧连接。通过改变3根肌腱的工作状态，可实现伸缩及3维任意方向的弯曲运动。2008年，Camarillo等研发了一种可控的肌腱驱动机器人作为心脏导管［4］。2009年，Chen研制了一种单段连续机器人［5］（Clobot），Clobot由硅胶材料制作而成，采用气压驱动，其内部圆周上均布有6个通道，三个为主驱动通道，另三个为被动通道。伺服阀通过主动通道驱动Clobot，实现2自由度弯曲运动，当Clobot在0.2MPa气压驱动下，可实现120°任意方向的弯曲。上述机器人采用连续型结构作为机器人的机械机构，而未涉及到刚性关节，本文结合刚性关节高负载和连续关节灵活度高的特点，提出一种混合型关节的结构设想，并基于传统机器人的分析方法，对混合关节的结构进行了分析研究，详细介绍了混合关节运动学分析与建模、控制分析与实验。

1　机构构型

1.1关节机构设计

机器人构型采用单刚性关节和单连续关节串联的连接方式。考虑到关节连接方式的不同，放置关节有两种情况，如图1所示。

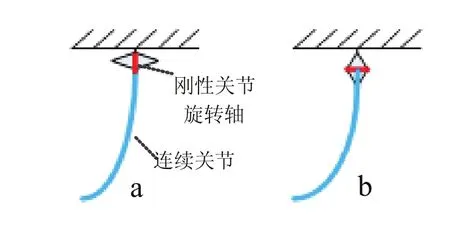
图1　a关节轴心线相重合，b关节轴心线相垂直

以这两种连接方式为骨架进行设计，可得到两种不同的混合关节机构，图中红色部分表示刚性关节旋转轴，蓝色部分表示连续关节。两种机构的工作性能和运动空间都有所不同，本文将建模分析两种连接方式下各混合关节机构的空间运动范围，并优选机器人的构型。

1.2 运动空间仿真与优化

建立连续关节数学模型，如图2所示。其中弧OO1为连续关节，其长度为L=43cm，固定连续关节端点O，末端O1为自由运动端，图中为连续关节在空间中的一种状态，其中连续关节在O点处的切线方向与z轴正方向重合，弦d与z轴正方向的夹角为β，其变化范围为（0，π），弧OO1在O-xy平面的投影与y轴的夹角为ɑ，其变化范围为［0，2π］，连续关节在纯力的作用下其弯曲变形符合弹性体常曲率变形理论。

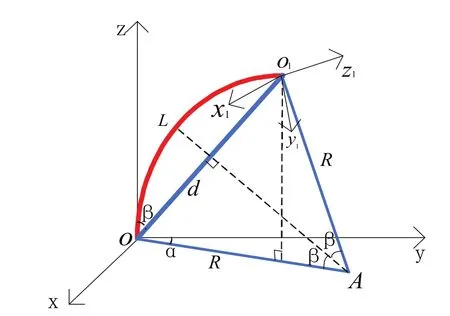
图2　连续关节数学模型

根据以上条件和几何关系可以得如下公式：

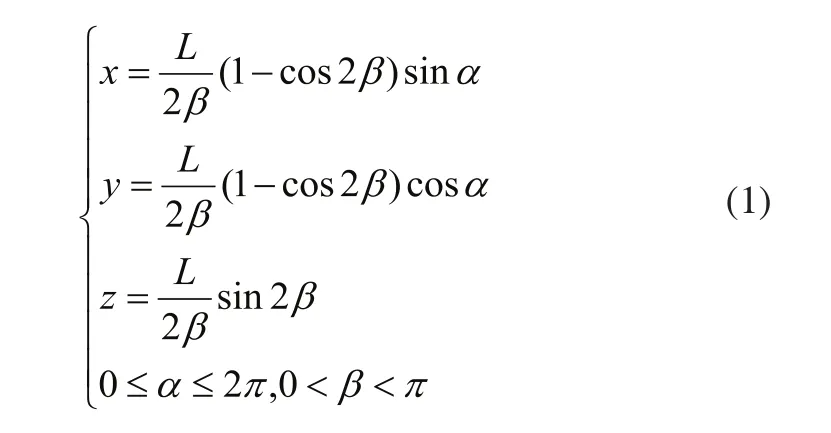
根据式（1），在MATLAB中绘制单连续关节端点O1的空间运动范围，如图3所示。

图3　连续关节下的运动空间范围

在O点处以图1（a）方式加入刚性关节时，在转动刚性关节轴时，连续关节与刚性关节绕同一轴心旋转，此种情况牺牲了刚性关节的一个自由度，与单纯的连续关节所能达到的运动空间范围相同，并没有起到扩大连续关节运动范围的作用。若按图1（b）方式在O点加入刚性关节，连续关节便可绕y轴进行旋转，设旋转角度为θ，θ的范围为（-π/2，π/2），此时公式可修改为：

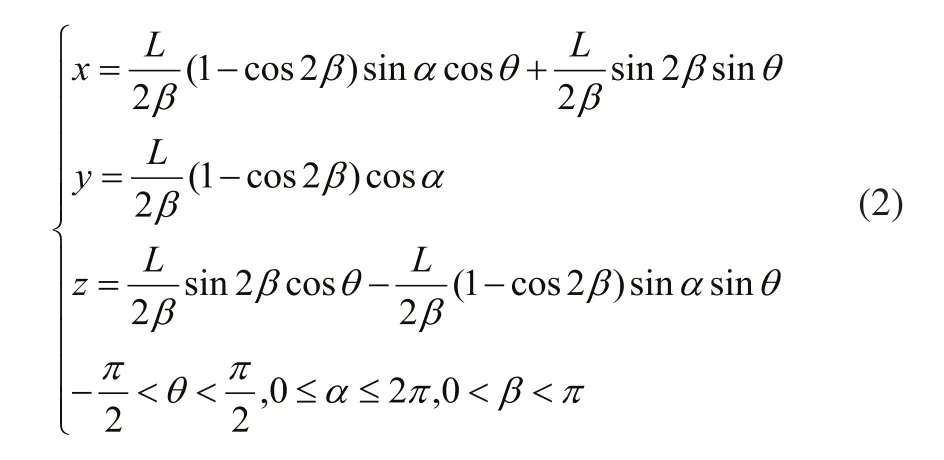
根据式（2）绘制出混合关节情况下，端点O1的空间运动范围如图4所示。

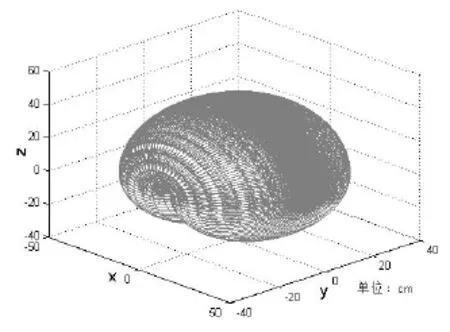
图4　混合关节下运动空间范围

对比图3和图4可知，采用第二种方式串联刚性关节和连续关节时，由于竖直方向z值最大，串联后z的空间最大值未发生变化，y轴为旋转轴，y的空间最大值也未发生变化，在MATLAB中可以得出x的最大值由原来的31cm增加到43cm，由此分析可知端点O1运动空间范围增大。因此，采用刚性关节旋转轴轴心线与连续关节轴心线直的串联方式作为机器人机构构型。

2　运动学建模与运动控制分析

2.1运动学建模

传统机器人各个关节都是刚性关节，运动学建模常采用D-H参数法建立各个关节的位姿关系。而由刚性关节和连续关节组成的混合关节则不能直接采用D-H参数法建立运动学模型，根据连续关节空间数学模型，坐标系O1-x1y1z1可由O-xyz坐标系先绕x轴旋转2β角，再绕z轴旋转ɑ角，最后沿弦方向平移到O1点即可。其中坐标点O1为），等效成刚性关节间的D-H变换表示为矩阵为2β） 和R2=Rot（z，ɑ），平移向量为因此由O-xyz坐标系变换到O1-x1y1z1坐标系的变换矩阵T1为：

其中，式中c代表cos，s代表sin，T1即为单连续关节空间坐标变换矩阵。

连续关节和刚性关节混合时，设连续关节所在基座为00-x0y0z0坐标系，基座中心到刚性关节轴的距离为d0，由00-x0y0z0坐标系先沿z0轴平移距离d0，然后再绕y0旋转θ角即可得到O-xyz坐标系，矩阵表示为T0，则T0可表示为：

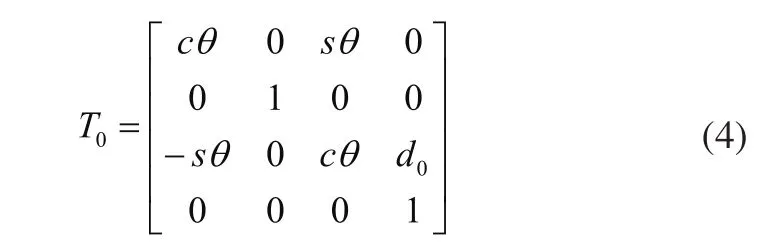
因此连续关节末端O1在基坐标系中的位姿可表示为：

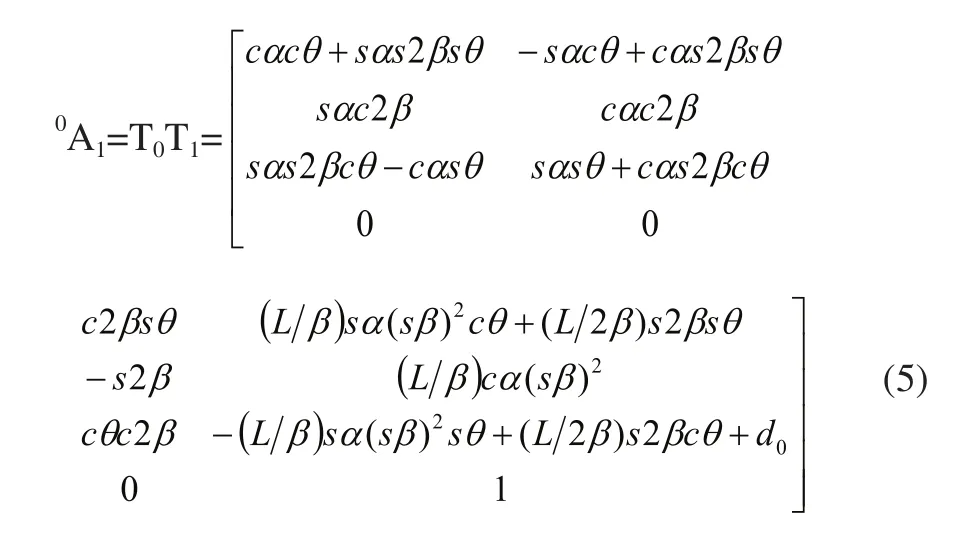
上式中s代表sin，c代表cos。设已知末端O1的位姿由矢量n、o、a、p在基坐标系x0、y0、z0轴的分量如下：

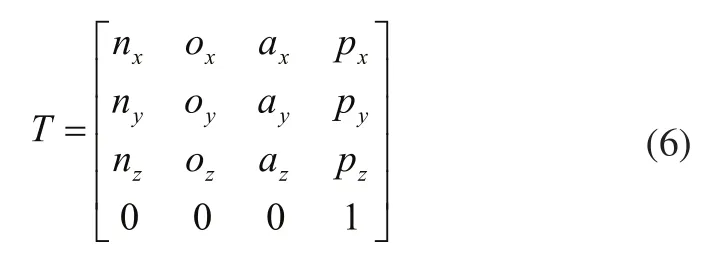
则0A1=T，根据对应元素分别相等和具体ax、ay、az、ny、oy的值可求得ɑ、β、θ的值。

2.2运动控制分析

本次混合关节设计采用刚性关节处电机直接驱动，连续关节采用互成1200的三根钢丝绳索驱动，连续关节的弯曲变形由固定在底座处的三个电机拉动绳索完成。

1）连续关节处绳索变化分析

确定驱动方式后，接下来分析绳索长度变化与ɑ、β、θ之间的关系，设三根绳索长度分别为L1，L2，L3，先确定只在连续关节下L1，L2，L3与ɑ、β之间的关系，设连续关节弯曲一定角度，绳孔到圆盘中心的距离为r，如图5所示。

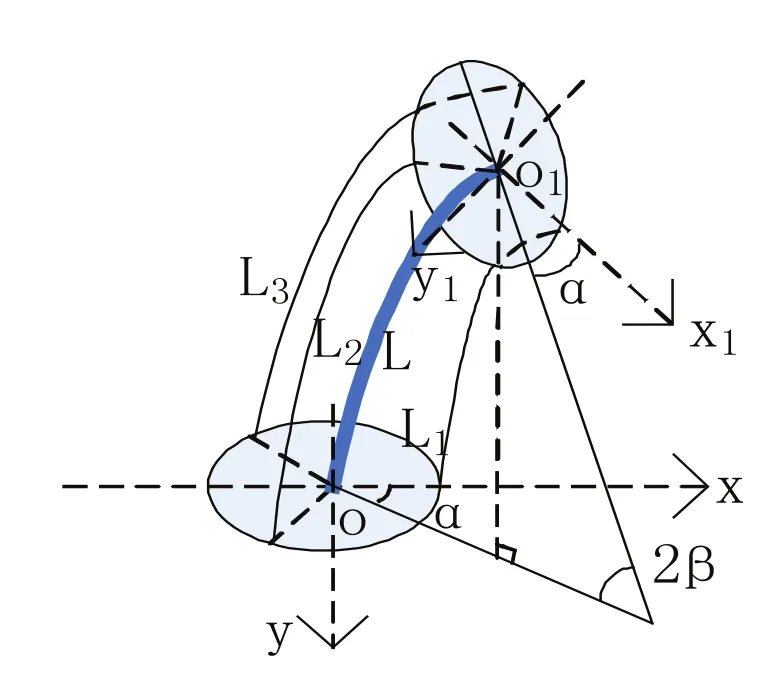
图5　连续关节弯曲下绳索变化

根据图5几何关系可推导出如下关系：

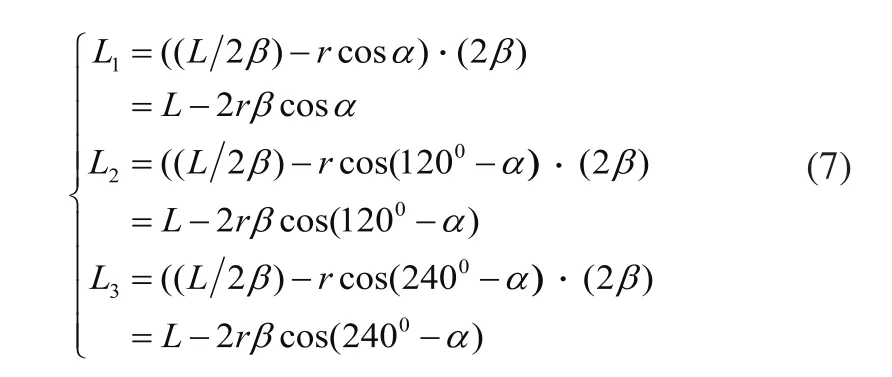
当ɑ、β变为ɑ1、β1时，绳索的变化量分别为ΔL10、ΔL20、ΔL30，则：

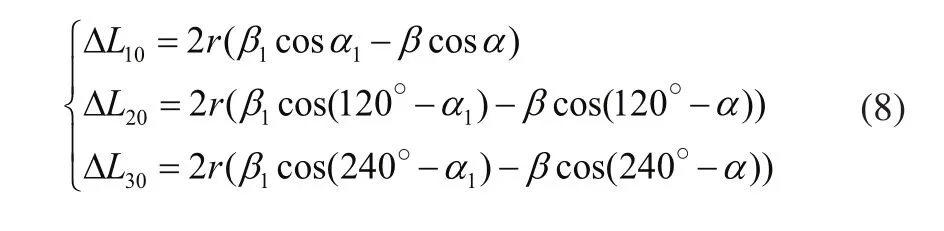
2）刚性关节处绳索变化分析

上下底盘之间的绳索在刚性关节旋转下的长度变化只与θ变化有关，刚性关节模型如图6所示。

根据刚性关节结构模型，其刚性关节旋转角θ与上下底盘之间绳索1的变化关系可等效为图7的几何关系。其中A点为下底盘上孔1的位置，B点为旋转轴，C点为上底盘上孔1的位置，D点为连杆BC绕旋转轴B旋转Δ θ后与C对应的点。

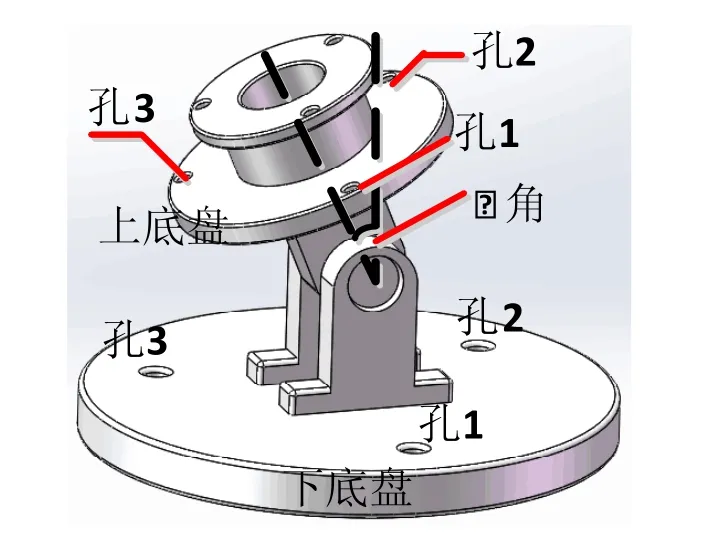
图6　刚性关节结构模型

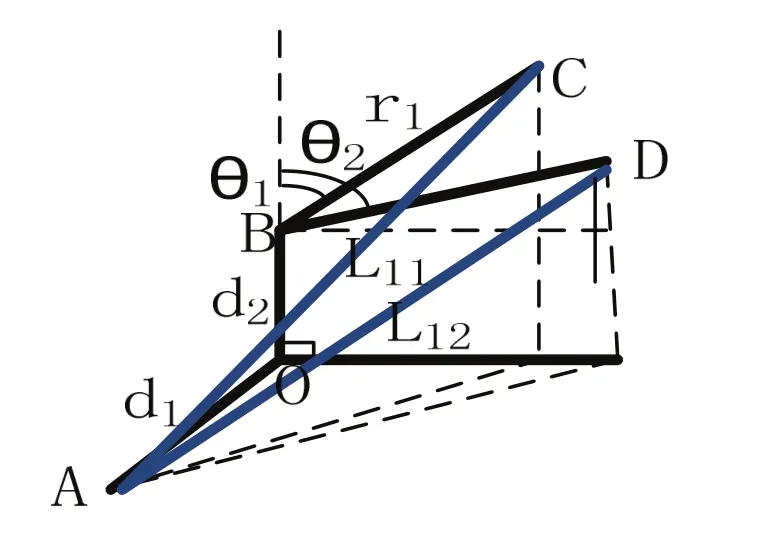
图7　旋转θ上下底盘间绳索1的变化

根据图7的几何关系可推导出如下关系，其中L11上下底盘间绳1的长度，L12为绕轴B旋转Δ θ后上下底盘间绳1的长度，ΔL11为旋转Δ θ后上下底盘间绳1的变化量。

由于绳索2和绳索3的位置是对称分布的，因此只需要得出其一与θ角变化的关系即可得出另一绳索与θ角变化的关系，可取绳索2为研究对象，其所在空间几何结构可简化如图8所示。

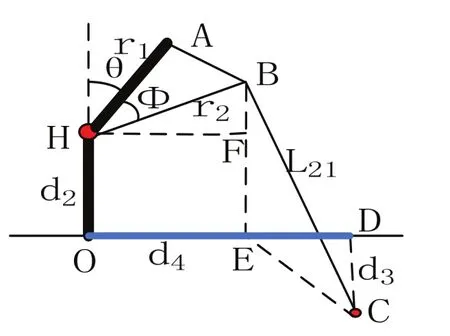
图8　旋转θ上下底盘间绳索2的变化

图中HB为上底盘孔2到旋转轴H的距离（即r2），r1为上底盘到旋转轴的距离，d2为下底盘到旋转轴的距离，HA与HO确定平面OHABE，C点为下底盘上的孔2位置，d3为下底盘孔2到平面OHABE的距离，d4为O点到点C到平面OHABE投影点D的距离，r1、r2、d2、d3、d4的距离可测量，Φ的大小计算可以得到，BC的长度即为上下底盘间绳索2的长度，由几何关系可得：其中L21为起始旋转角度θ时上下底盘间绳索2的长度，L22为旋转角度变为θ1时上下底盘间绳索2长度，ΔL21为旋转角由θ变为θ1时上下底盘之间绳索2变化量。同理可得：

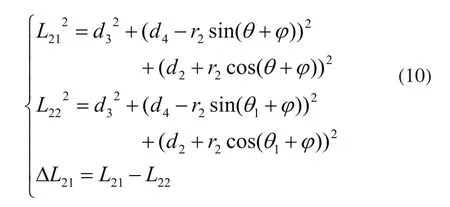
3）绳索总变化长度

由1）、2）可得绳索总变化长度为：

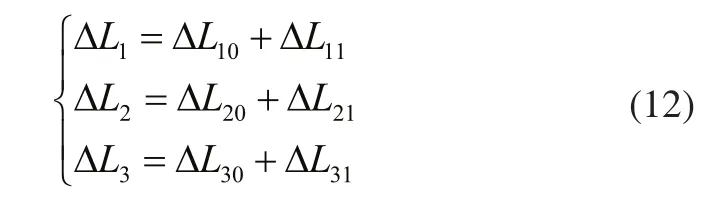
通过控制电机使绳索变化ΔL1、ΔL2、ΔL3，即可使末端端点达到预定位置。

3　机器人控制系统设计

为了实现对整机的控制，使混合关节连续型机器人按照规定的轨迹运行，必须对4个步进电机进行协同控制，采用基于两级分布式控制策略构建整机的控制系统，其结构框图如图9所示。

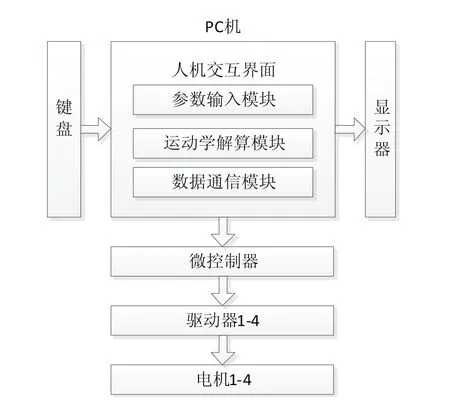
图9　两级分布式控制系统框图

其中，上层控制器PC机用于实现人机交互和运动学解算。利用VC++开发的基于Windows平台的人机交互界面，用于实现混合关节连续型机器人运动参数的输入，运动学解算模块根据输入的末端位姿参数对各关节运动角度和绳索变化量进行计算，将处理后的各绳索变化参数送入微控制器stm32f103中。

下层控制器由微控制器stm32F103和4个步进电机驱动器组成。根据绳索变化参数对电机转动量进行归算，微控制器又根据电机的转动量向各个电机驱动器发送相应的脉冲量，从而控制各个步进电机转动，使混合关节末端向预定的位置运动。为了检测末端位置是否达到预定要求，采用NDI三维动态坐标测试系统对末端位置进行检测，如果末端位置不在误差范围之内，根据检测到的末端位置作为起始状态，原预定位置仍为最终状态，进行新的参数输入计算，进一步修正末端位置误差，其控制流程图如图10所示。

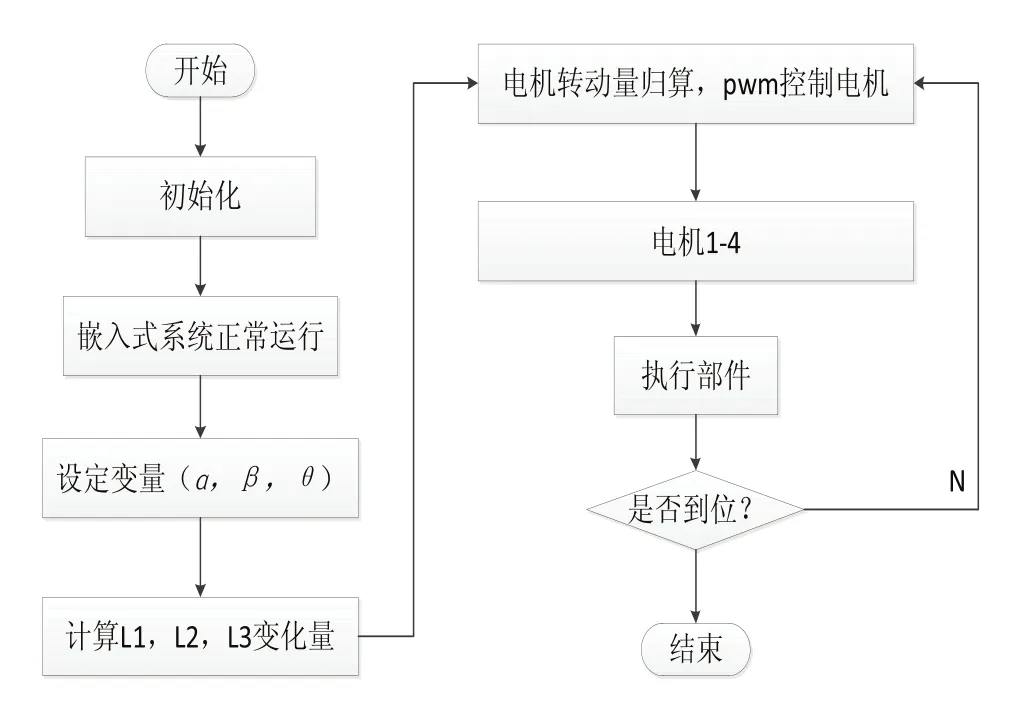
图10　控制流程图

4　实验与结果分析

用MATLAB对上述模型进行运动学仿真，假定初始关节角为（α，β，θ），初始关节角的两个量不变，另一个角度由300-600-900变化的情况下，求取机器人关节末端端点的理论位置坐标，并在MATLAB中绘制其末端理论运动轨迹。在原理样机中驱动对应绳索变化量，测量并记录原理样机末端端点实际位置坐标，以这些坐标点为实际离散采样点，对采样点进行三次样条曲线拟合，并在MATLAB中拟合出原理样机末端端点实际运动轨迹图，如图11～图13所示。

图11～图13中，红色曲线为机器人末端理论位置轨迹，带*的蓝色曲线为末端实际离散采样点拟合的轨迹，*表示采集的样点。通过对机器人关节末端理论位置运动轨迹曲线与实际离散采样点拟合曲线对比分析，在MATLAB中做出两者之间的误差曲线图，如图14 （a、b、c三条曲线分别对应图11～图13），并求出两者之间均值和方差，以此验证运动模型的可行性。

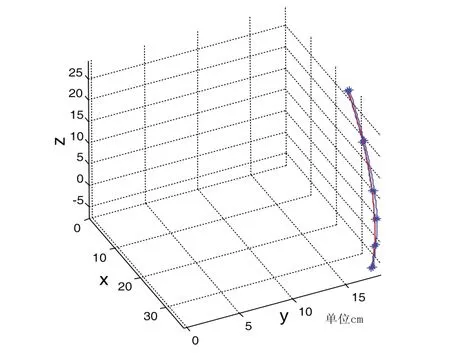
图11　θ变化时末端理论和实际位置轨迹曲线

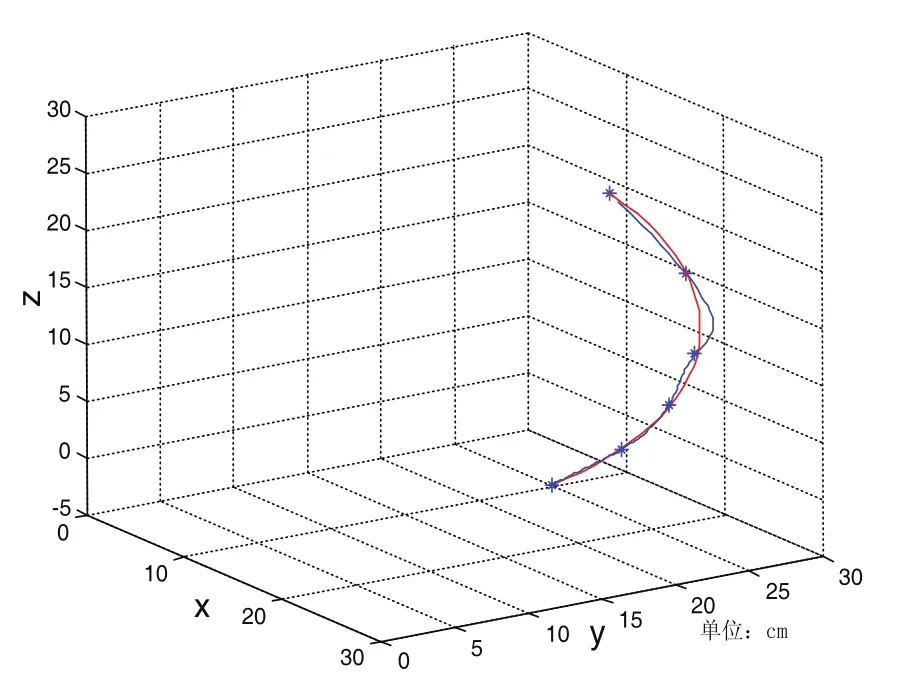
图12　β变化时末端理论和实际位置轨迹曲线

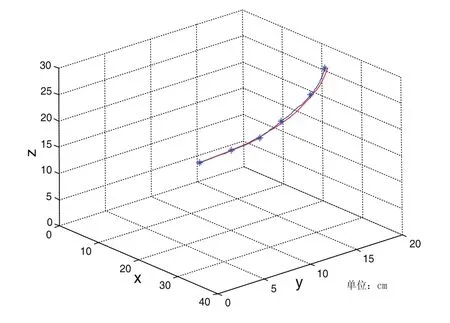
图13　α变化时末端理论和实际位置轨迹曲线

经计算，分别得到相应的误差为0.8 0 7 7± 0.4022，5.1102±2.9975，2.9715±1.4907（mm）。由此可知，机器人末端实际运动轨迹基本符合理论运动轨迹，从而验证了理论模型的可行性。

【】【】

图14　a、b、c为图11～图13的误差曲线

5　结论

本文提出一种新型混合关节机器人构型，即机构由刚性关节与连续关节串联构成，从理论上验证了采用这种方式的优越性，并对构型进行运动学建模分析和分布式控制系统设计，制备了原理样机模型，并对机器人

末端理论位置轨迹和实际位置轨迹进行实验对比，分析之间存在运动误差，充分说明了机器人机构设计的可行性，也进一步提升了机器人的运动空间、灵活性和运动精度。

［1］ Robinson G，Davies J B C.Continuum robots-a state of the art［A］.Robotics and Automation，1999.Proceedings. 1999 IEEE International Conference on.IEEE［C］.1999，4：2849-2854.

［2］ 陈丽，王越超，马书根，李斌.蛇形机器人行波运动的研究［J］.机械工程学报，2004，40（12）：38-43.

［3］ Choi D G， Yi B J， Kim W K. Design of a spring backbone micro endoscope［A］.Intelligent Robots and Systems，2007.IROS 2007. IEEE/RSJ International Conference on.IEEE［C］.2007：1815-1821.

［4］ David B.Camarillo，C.F.Milne，Christopher R. Carlson，Michael Zinn，J. Kenneth Salisbury. Mechanics Modeling of Tendon-Driven Continuum Manipulators［J］.IEEE Transactions on Robotics，2008，24.

［5］ G. Chen，Minh Tu Pham，Tanneguy Redarce.Sensor-based guidance control of a continuum robot for a semi-autonomous colonoscopy［J］.Robotics and Autonomous Systems，2009，57.

Research of the mechanism configuration and
motion control for the cable-driven hybrid joint robot

TP242

A

1009-0134（2016）08-0036-05

2016-06-12

国家科技支撑计划（2015BAK06B02）

李亚锋（1989 -），男，河南项城人，硕士，研究方向为电机及其控制。