求解动态车间调度问题的改进微粒群算法

吴再新，高尚策，2，齐 洁

（1.东华大学 信息科学与技术学院，上海　201620；2.富山大学 工程学院，日本 富山　9308555）

求解动态车间调度问题的改进微粒群算法

吴再新1，高尚策1，2，齐 洁1

（1.东华大学 信息科学与技术学院，上海201620；2.富山大学 工程学院，日本 富山9308555）

为了对生产车间调度过程中发生的动态事件进行快速、有效的处理，提出了一种将微粒群算法与遗传算法（GA）、模拟退火算法（SA）相结合的混合微粒群算法（GSPSO）。通过用标准车间调度问题对该算法的性能进行检验；然后把该算法用于解决基于事件驱动调度策略的动态车间调度问题；仿真结果表明GSPSO算法具有快速的收敛性和可行性，能对生产过程中发生的动态事件进行合理调度。

动态车间调度；粒子群算法；遗传算法；事件驱动

对生产作业车间进行有效的调度是制造执行系统的一项核心技术，也是研究的一个热点问题。作业车间调度问题（JSP）实际上就是组合优化问题，也是一类典型的NP难题，它可以分为两种：静态调度和动态调度。在过去的几十年里，大部分学者对于车间调度问题的研究都是静态的。在实际的生产过程当中，各种突发事件（如新增紧急订单、订单取消、机器故障等）时常发生，因此动态作业车间调度更加符合实际的情况。

在求解JSP问题的方法上，遗传算法凭借其强大的全局搜索能力，被许多学者用于解决JSP问题[1]，但是该算法有收敛速度慢、容易早熟的缺点；蚁群算法主要针对调度问题产生，其在解决JSP问题上也得到了大量的应用[2]，该算法对大规模调度问题很难得到最优解，且求解时间过长。粒子群优化算法是Dr.Eberhart与J.Kennedy于1995年正式提出[3]，之后得到了迅速的发展和广泛的应用，文献[4]采用微粒群算法与遗传算法相结合，提出了改进的微粒群算法用于解决模糊车间调度问题，但是对算法跳出局部最优的策略仍待改进。在前人研究的基础上，把遗传算法交叉变异特性和模拟退火算法的metropolis接受准则引入到PSO算法中，提出了混合微粒群算法（GSPSO）用于解决作业车间调度问题。

1　动态车间调度（DJSP）

JSP问题可以简单的描述为:有n个工件在m台机器上进行加工，每个工件有一道或者多道工序等待加工，每道工序只能在指定的机器上进行加工，且满足以下的约束条件[5]：

1）每个工件的加工工序不能改变。

2）每个工件的加工时间和机器事先已经确定。

3）同一工件同一时刻只能在一台机器上进行加工。

4）一台机器同一时刻只能加工一个工件。

调度的目的就是找到一个合适的加工序列，在满足上述约束条件的情况下，使得最大加工完成时间最小。所谓最大加工完成时间就是所有工件中最后一道工序加工完成的时间，可用式（1）表示：

其中，表示最佳的调度方案，表示工件最后一道工序的完工时间。

在实际的生产过程中，一些随机的动态事件比如新增紧急订单，订单取消，机器故障维修等在所难免，在任务执行过程中必须实时监测这些随机事件的发生，然后对加工任务执行重新调度，使得调度系统始终处于最优状态。这样，原本是静态的作业车间调度就变成了动态调度。解决动态事件的策略有两种[6]，一是基于事件驱动的调度策略，即在系统动态事件发生时就立即进行重调度。二是周期性的调度策略，即不管有无动态事件发生，系统总是每隔一段时间进行一次重调度。在实际的生产应用当中，应视情况而选取不同的调度策略，当已知系统会周期性的出现动态事件（如定期机器维修）时，应采用周期性调度策略；当系统对动态事件处理的实时性要求比较高时应选取事件驱动的调度策略。为了使最大完工时间最小，又要使系统对动态事件做出及时的响应，减少重调度带来的时间损耗，本文选用基于事件驱动的调度策略。

2　GSPSO算法描述

2.1标准微粒群优化算法

微粒群优化算法是基于群体寻优的进化算法，它将每个个体看作是D维搜索空间中的一个没有体积的微粒，每个微粒都代表极值优化问题的一个潜在最优解，用位置、速度和适应度值三项指标表示该微粒的特性适应度值由适应度函数计算而来，其值的好坏表示粒子的优劣。微粒在解空间中运动，通过跟踪个体极值Pbest和群体极值Gbest更新个体位置。个体极值Pbest是指个体所经历位置中计算得到的适应度值最优位置，群体极值Gbest是指种群中所有粒子搜索到的适应度最优位置。其优化过程可用下式表示[7]：

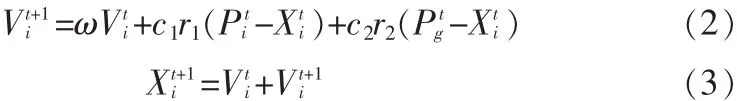
其中，为惯性权重，为粒子速度，、为非负常数，称为加速度因子，和是分布在[0，1]区间的随机数。标准微粒群寻优算法的基本流程图如图1所示。

图1　标准微粒群算法流程Fig.1　The standard PSO algorithm flow chart

2.2GSPSO算法概述

微粒群优化算法是针对连续优化问题提出，而要用于解决离散问题必须对算法进行改进。由式（2）和式（3）可知，微粒具有自身的认知能力和社会信息共享能力，这也是种群进化的依据。为了能使用PSO算法对离散的JSP问题进行处理，文中提出了式（4）用于粒子更新：

式中表示粒子的第t+1次迭代，、分别表示粒子的个体极值和种群的群体极值，茚代表遗传算法的交叉操作，、分别代表粒子与、交叉时交叉片段的长度，他们的取值范围是0到微粒的最大长度。由此可知，为粒子的自身的认知能力，为种群的社会信息共享能力，而则表示当前粒子的权重。

标准的PSO算法具有快速的收敛能力，但是容易陷入局部最优解。将SA算法的metropolis接受准则融入到PSO算法中，使算法具有突跳能力，能有效的避免搜索过程陷入局部最优解。把GA算法的变异操作作用于PSO算法的全局最优解，增加种群的多样性，能使算法得到全局最优解。GSPSO算法同时继承了3个算法的优点，使得它能够快速的在全局范围内寻找最优解，又能避免算法在搜索过程中陷入局部最优解。GSPSO算法的解决动态车间调度问题的基本步骤如下：

Step1：种群初始化，初始种群寻优

采用基于工序的编码方式随机生成初始微粒种群，通过适应度值函数对微粒进行评价，找出所有微粒的最佳个体，记为种群的最优个体，所有粒子的个体最优记为各自的初始位置。

Step2：SA算法Metropolis接受准则

将SA算法的Metropolis接受准则作用于个体最优微粒，避免算法陷入局部最优解。

Step3：遗传算法的交叉与变异

把遗传算法的交叉操作引入到PSO算法中粒子的进化过程当中，用交叉产生的新个体代替粒子的速度和位置的更新。同时把遗传算法的变异策略作用到全局最优微粒，以避免算法陷入局部最优，增加种群的多样性。

Step4：最优选择

当算法达到算法的终止条件后，采用第二步选出来的全局最优粒子作为种群的最优值Gbest，选出最优值之后调度任务就可以顺利进行了。当动态事件出现，调度任务被打断时，进入第五步。

Step5：动态事件处理

通过动态事件发生的时刻可以确定待加工的工件和机器的状态，重新进入第一步进行重调度。

2.3GSPSO算法的具体实现

GSPSO算法处理作业车间动态调度问题的算法流程图如图2所示。

2.3.1适应度值函数

PSO算法是通过适应度值函数来对个体的自身性能及种群的整体性能进行评价的，根据适应度的大小对个体进行优胜劣汰的选择，进而决定个体的下一步操作。由于本文以调度任务的最大完工时间最少为优化目标，因此可以用式（1）的倒数作为算法的适应度值评价函数，即：

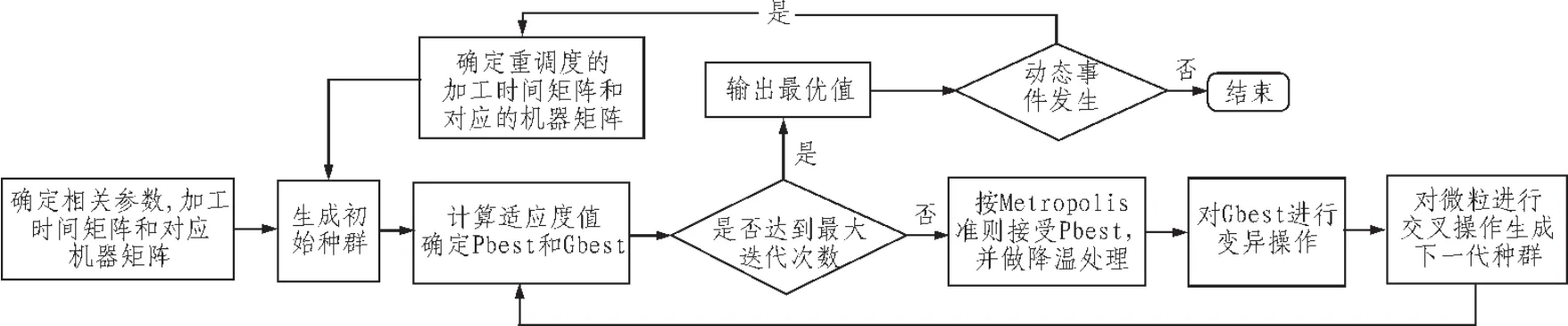
图2　GSPSO算法流程图Fig.2　The GSPSO algorithm flow chart

2.3.2Metropolis抽样准则

在PSO算法中引入Metropolis准则，它能以一定的概率接受恶化解，这样就能使算法跳离局部最优的陷进。接受概率是这样确定的，假如调度任务最小的最大完工时间为f（t），则当前解最小的最大完工时间为，新解最小的最大完工时间为，两者的差值为，则Metropolis准则接受概率为：

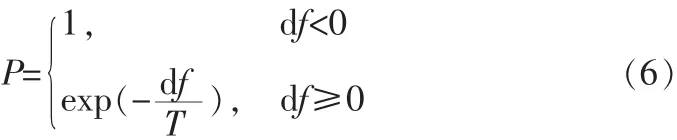
如果df<0，则以概率1接受新解；否则以概率exp（）接受新解。

2.3.3粒子的编码规则

由于调度问题具有严格的工艺约束，必须以一定的编码方式来体现其工艺约束，以便用微粒群算法对其进行处理。文中采用基于工序的编码方式对调度任务进行编码，该编码方式进行编码时，用同一数字表示工件的工件号，用该数字在微粒中第几次出现来表示该工件的工序号。例如以一个3*3的作业车间调度问题为例，有一个粒子的编码为232133211，该编码的第一个数2表示2号工件的第一道工序，第二个数3表示3号工件的第一道工序，第三个数2表示2号工件的第二道工序，以此类推。

2.3.4遗传算法的变异与交叉操作

为了使算法能够在全局范围内搜索最优解，避免进入局部最优解，增加种群的多样性，对PSO算法中的以一定的概率进行变异操作。传统遗传算法的变异概率是固定不变的，从而使得算法难以跳出局部最优，文中提出一种新的计算变异概率的式（7），

式中为第i次迭代的变异概率，为初始变异概率，为第i次迭代中的适应度值函数，、分别为的最大适应度值函数和平均适应度值函数。这种方法能提高适应度值劣于平均适应度值微粒的变异概率，抑制适应度值优于平均适应度值微粒的变异概率。变异的方法是随机的交换微粒中若干对工序的位置。

在PSO算法中，采用遗传算法的交叉操作替代PSO算法的种群更新，可以有效的把其应用于解决离散的JSP问题。在交叉的过程中，先让微粒与Pbest交叉，交叉的方法是根据式（4），在Pbest中选取一段，插入到当前微粒的对应位置，然后再把此微粒与Gbest进行交叉，交叉的方法与前面相同。这样在交叉后就得到了新的微粒，新的微粒既保存的上一代微粒的信息，又具有信息共享的能力。以一个3*3的车间调度问题为例，假设式（4）中常数、都为2，则一个微粒的交叉过程可用如图3来描述，交叉后会出现某些工件的工序多余，某些工件的工序缺失的现象，把工件工序多余的操作变为工件工序缺失的操作，使得交叉后的微粒符合编码规则。

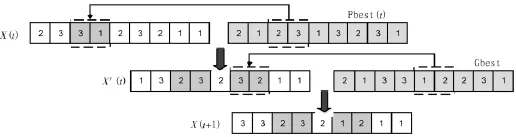
图3　微粒交叉Fig.3　The cross of particle

2.4动态作业车间调度的实现过程

在调度系统的执行过程当中，由于调度环境的动态变化，需要对加工任务进行重新调度。重调度与初始时刻调度的主要差别是机器状态和加工的工件任务不同，机器的可利用时候和工件上一道工序的完成时刻不同。在重调度时刻，有的机器可能正在加工工件，由于加工过程的连续性，只有待机器加工完该工序，才能进入重调度的调度安排；而有的机器可能在重调度时刻处于空闲状态，重调度之后立即可以投入生产；有的工件可能完成了一部分工序，也有可能完成了全部工序。处理动态事件的步骤如下：

Step1：系统按照调度方案进行加工，动态事件发生时进入第二步，如果加工任务完成没有动态事件发生，结束调度任务。

Step2：确定重调度加工工件的工序矩阵和对应的机器矩阵，通过动态事件发生的时候和初始调度情况计算机器的可利用时刻矩阵。

Step3：产生重调度方案，转入第一步，调度任务继续执行。

3　实验仿真与分析

实验仿真在自用PC机上进行，用benchmark车间调度问题对算法进行测试，算法的基本参数设置如下：

种群迭代次数，种群规模，粒子交叉片段常数、问题的规模大小不一适当变化，变异初始概率，模拟退火初始温度，降温系数。

表 1是用本文提出的算法和 PSOGA、GA算法解决benchmark车间调度问题10次，然后取平均值的比较。从表中可以看出，本文提出的PAGSO算法与另外两种算法相比具有更好的平均值，从而表明该算法在求解JSP问题上具有很好的求解效果。

图4是3种算法在求解FT06问题时的收敛性比较，图中横坐标表示算法的迭代次数，纵坐标表示最大完工时间10次的平均值。从图中可知，PSGSO算法具有更快的收敛速度。

表1　三种算法的比较Tab.1　Comparison of the three algorithms

图4　三个算法的收敛性比较Fig.4　The convergence comparison of the three algorithms

图5是用本文提出的PSGSO算法解决DJSP问题时的输出甘特图，图中横坐标表示加工时间，纵坐标表示机器号。限于篇幅只考虑以下3种动态事件发生的情况：

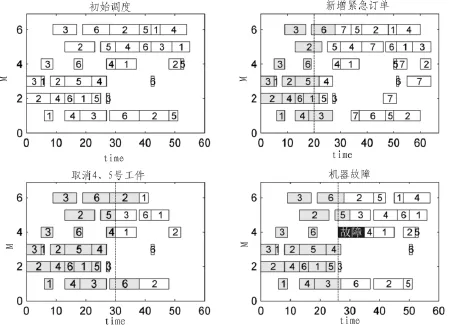
图5　动态调度甘特图Fig.5　The gantt chart of the dynamic job-scheduling

1）新增紧急订单。在t=20时刻，新增紧急订单7号工件，该工件工序的时间约束矩阵为T7=[6 3 8 5 4 9]，对应的机器约束矩阵为M7=[6 1 5 2 4 3]，由图可以看出紧急订单加入后被优先处理，最终的调度结果为64。

2）在t=30时刻，取消4号和5号工件，由图可知在30时刻后工件4和工件5的已经从调度任务中取消，最终的调度结果为52。

3）在t=26时刻，机器4出现故障，预计修复时间为9，最终调度结果为57。

文献[8]中用混合蚁群算法解决同样的问题，与本文采用的方法比较如表2所示，结果表明GSPSO算法具有明显的优势，说明该算法具有可行性。

表2　混合蚁群算法与GSPSO算法处理DJSP问题时的比较Tab.2　The comparison of ant colony algorithm and GSPSO algorithm to deal with DJSP

4　结束语

文中把遗传算法的交叉、变异操作和模拟退火算法的Metropolis接受准则融入到粒子群[9-11]优化算法当中，形成了混合粒子群算法GSPSO，该算法能自适应的调整变异概率，在全局范围内高效地搜索最优解。通过实验结果表明该算法对小规模的JSP问题具有很好的搜索质量和较快的收敛速度，能对车间调度生产过程中发生的动态事件进行及时有效的处理；但是对大规模的JSP问题是否能取得好的效果还有待验证，这也是今后研究的重点内容。

[1]ZHAO Zi-xiang，ZHANG Guo-shan，BING Zhi-gang.Jobshopscheduling optimization design based on an improved GA[C]//2012 10th World Congress on Intelligent Control and Automation（WCICA）.Beijing:IEEE，2012:654，659.

[2]雷蕾.基于混合蚁群算法的动态JSP研究与仿真[D].西安：西安工业大学，2012.

[3]Eberhart R，Kennedy J.A new optimizer using particle swarm theory[C]//Proceeding of the Sixth International Symposium on Micro Machine andHuman Science.Nagoya:IEEE，1995: 39-43.

[4]Niu Q，Jiao B，Gu X S.Particle swarm optimization combined with genetic operators for job-shop scheduling problem with fuzzy processingtime[J].Applied Mathematics and Computation，2008，205（1）:148-158.

[5]CHIANG Tsung-Che，FU Li-Chen.Multiobjective Job Shop Scheduling using Genetic Algorithm with Cyclic Fitness Assignment[C]//IEEE Congress on Evolutionary Computation. Vancouver BC:IEEE，2006:326-3273.

[6]SureshV，ChandhuriD.Dynamic Scheduling-A survey of research[J].Int Jof Prod Peon，1993，32（1）:53-63.

[7]YAN Ping，JIAO Ming-hai.Animproved PSO search method for the job shop scheduling problem[C]//Control and Decision Conference.Mianyang:IEEE，2011:23-25.

[8]陆韡，张洁.基于事件及变周期驱动的作业车间动态调度[J].控制工程，2007（S1）:209-213.

[9]孙会明，陈薇.基于粒子群优化的光伏MPPT算法[J].电子科技，2014（8）:187-189.

[10]康鲲鹏.快速混合粒子群优化算法应用研究[J].电子设计工程，2014（10）:10-13.

[11]王娟娟.哈夫曼编码的协同粒子群优化算法[J].计算机与现代化，2015（6）:82-85.

An improved particle swarm optimization algorithm for dynamic job-shop scheduling problem

WU Zai-xin1，GAO Shang-ce1，2，QI Jie1
（1.College of Information Science and Technology，Dong Hua University，Shanghai 201620，China；2.Faculty of Engineering，University of Toyama，Toyama 9308555，Japan）

In order to deal with the dynamic events rapidly and effectively in the process of job-shop scheduling，an improved hybrid Particle Swarm Optimization algorithm（GSPSO）combining with Genetic Algorithm（GA）and Simulated Annealing algorithm（SA）has been proposed.The introduced algorithm is tested by the benchmark job-shop problem（JSP），then，the hybrid algorithm is used to solve the dynamic JSP problem which based on the event driven scheduling strategy.The results of the simulation shows the good convergence and feasible of the improved algorithm，and it can make a good performance in dealing with the uncertain dynamic events.

dynamic job-shop scheduling；particle swarm optimization algorithm；genetic algorithm；event driven

TP18

A

1674－6236（2016）01-0026-05

2015-05-09稿件编号：201505080

国家自然科学基金项目（61203325）；上海启明星计划项目（14QA1400100）

吴再新（1990—），男，湖南娄底人，硕士。研究方向:人工智能与智能控制。