基于小波和过程神经网络的时间序列预测模型

刘修恒，吕　鑫，戚荣志，刘　璇，马鸿旭

（河海大学计算机与信息学院 江苏 南京　211100）

基于小波和过程神经网络的时间序列预测模型

刘修恒，吕鑫，戚荣志，刘璇，马鸿旭

（河海大学计算机与信息学院 江苏 南京211100）

提出基于过程神经网络和自回归模型的组合预测方案。首先，采用二进正交小波变换对原始时间序列分解和重构，分离出原始序列中的高频部分和低频部分；然后对低频部分构建过程神经网络模型，对低频部分采用自回归模型；最后将两种模型的预测值叠加，得到原序列的预测值。

小波分解；非平稳时间序列；过程神经网络；自回归；预测

在现实生活中，非平稳和非线性的时间序列随处可见，我们并不清楚动力系统变量是如何相互作用的，也不清楚它们如何支配系统的演化的，但这些变量的时频性是不相同的。模型的好坏对于动力学系统影响巨大，因为它有着重要的理论意义和很大的应用情景。

现如今，世界各地的专家和学者对时间序列的预测和辨识从不同方面进行研究。对于传统基于统计学的方法，其方法与结论的性能取决于样本的数量，然而实际情况中，样本的数量往往是有限的，这就使得传统基于统计学的方法无法取得很多的效果。由于强大的函数逼近能力与学习能力，人工神经网络较多地应用到时间序列预测中，但是因为输入的同步瞬时性的特点，因此人工神经网络对于序列中真实存在的时间累积效应难以表达。过程神经网络，由于其在传统人工神经网络的基础之上增加了一个时间聚合运算算子，因此过程神经网络可以充分体现序列中的时间累积效应。

如何提取原始序列中的低频和高频信息并建立模型和序列中的时间累积效应如何表达是有趋向性均值的非平稳时间序列预测的重要问题。二进正交小波对这种时间序列有着较好的适应性[2，8-9]，对低频的分离作用及有着较好应用能力的过程神经网络，为了解决这类预测问题，文中提出基于小波变换的过程神经网络和自回归的组合预测模型。

1　预测原理及方法

1.1过程神经网络

过程神经网络，其在网络结构上与传统人工神经网络类似，时变函数是两种网络的区别。由于在传统神经网络的基础上多了时间聚合算子，因此过程神经网络能充分体现原始序列中实际存在的时间累积效应。

1.1.1过程神经元

聚合、激励、加权组成了过程神经元，图1是其结构图。对于过程神经元来说，其输入和权皆为时变函数，这就使得其不仅有空间上的聚合，还有对时间的聚合。

图1　过程神经元Fig.1　Process neural

1.1.2过程神经网络拓扑结构

图2为具有一个隐层的过程神经网络的结构图。其中隐层是有过程神经元组成。

图2　3层过程神经元网络Fig.2　Three layer process neural networks

网络输出：

其中，wij（t）是第一层（输入层）的第i个神经元到第二层（隐层）的第j个神经元的权函数，vj是第二层（隐层）第j个神经元到第三层（输出层）神经元的连接权，τ、θj分别是输出层和隐层的阈值，f（·）、g（·）分别是隐层、输入层的激励函数，[0，T]为采样间隔。取，g（x）=x，τ=0，网络输出变为

1.1.3时变函数的展开

过程神经网络权值及输入皆为时序函数，取正交基函数为{d1（t），d2（t），…，dL（t）}，此正交基可以为小波基函数，三角基函数等.将时变函数输入和权按照一定的精度要求在此选择的正交基上进行有限展开，得到，，有

则输出变为

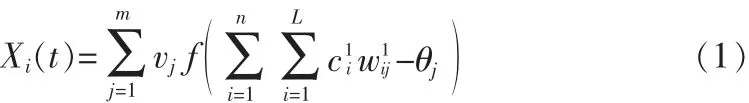
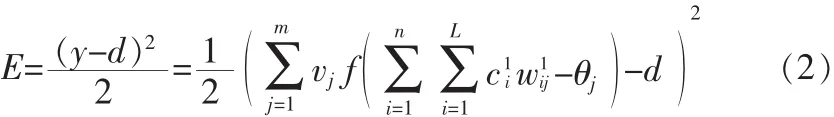
取样本：X（t）={x1（t），x2（t），…，xn（t），d}，则其误差函数：因此运算得到了简化，其中参数、vj、θj都是定量值，并且以上参数是输出y和误差函数E的自变量。

1.2二进正交小波变换的Mallat算法

1.2.1分解算法

若将设为10原始信号，则由小波变换的Mallat分解算法，有：

其中:G和H分别为高通滤波器和低通滤波器；1j和hj为原始信号在分辨率2-j下的低频信息和高频信息；最大的层数为J。最终原始信号分解为h1，h1，h3，…，hJ和1J。

因为该小波分解采用二抽取的形式，使得每次的分解，信号的长度就会减少一半，但是最后的输出长度和原始信号长度一致，而且信号长度的减少对于预测来说是不精确的，因此需要采用小波重构算法进行重构。

1.2.2重构算法

通过上一步，使得误差函数公式中的时序变化量没有了，

其中:H*和G*是对偶算子；j=J-1，J-2，….，0。

对小波Mallat分解后的信号利用式（4）重构采，这样信号个数可以增加。对h1，h2，h3，…，hJ和1J分别进行重构，得到H1，H2，H3，…，HJ和LJ，有

其中:H1:{h1，1，h1，2，…}，…，HJ:{h1，1，h1，2，…}为重构高频信号；LJ:{1J，1，1J，2，…}为重构低频信号。

1.3基于Mallat算法的PNN-AR预测方法

采用二进正交小波变换对原始时间序列分解和重构，分离出原始序列中的高频部分和低频部分；然后对低频部分构建过程神经网络模型，对低频部分采用自回归模型；最后将两种模型的预测值叠加，得到原序列的预测值。预测模型框架如图3所示。

图3　基于Mallat算法的Process-AR预测框架Fig.3　Process-AR prediction framework based on Mallat algorithm

令Xt:{X1，X2，…}为原始时间序列，对其进行小波Mallat分解以及对各层分解信号进行重构，得到

其中:H1:{h1，1，h1，2，…}，…，HN:{hN，1，hN，2，…}为重构高频信号；LN:{1N，1，1N，2，…}为重构低频信号。有：

若已知{ti|i≤M}时刻的Xi值，用其来预测k步以后的值，则需要解XM+k，即

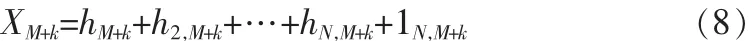
由于H1，H1，H3…HN可近似被当成平稳的时间序列，可分别对其建立 AR（p）模型，并对h1，M+k，h2，M+k，…，hh，M+k进行预测。其预测步骤如下：

1）对Hj建立自回归模型AR（p），根据已有的h*j，M+k的值对模型的参数进行估计，其中，1≤j≤N，i≤M；

2）检验上述模型的适用性；

3）利用适用性最好的AR（p）进行预测，得到hj，M+k的预测值

由于低频信号LN具有长期趋势和非线性的特点，可以利用过程神经网络对低频信号进行建立预测模型。根据上述过程神经网络原理，其具体步骤如下:

1）对网络的层数、各层神经元的个数进行设定，即确定网络的物理结构；

2）对网络各层的激励函数进行确定；

3）根据时间序列数据的特点选择一个合适的正交基函数θj，1=1，2，…，L，同时设定其个数；

4）根据选定的正交基函数展开所有样本

5）给网络参数ε、s=0、θj赋于初始值（i=1，2，…，n；j=1，2，…，m；1=1，2，…，L）

6）对误差精度ε、最大迭代次数M，累积迭代次数s=0，学习速率初始值η进行指定

7）对所有样本都按照如下步骤进行操作：

①取样本集中的样本1=1，2，…，L，从而可以得到该样本内元素Li（t），i=1，2，…，n在正交基函数上的展开系数a1i，1= 1，2，…，L；

②利用式（1）、（2）计算输出y以及误差函数E的值；

8）当E<ε或s>M时转9），否则转7）。

9）输出学习结果，结束。

2　预测实例

水文数据是一种用于判别和比较预测方法以及具有趋向性特点的非平稳的时间序列，如图4所示。利用六合水库的日水位数据来对文中提出的预测模型进行验证，并将其与单纯的过程神经网络模型比较。首先对原始序列利用db4小波进行2层分解与重构，然后使用PNN-AR（过程神经网络和AR组合模型）进行预测。利用均方误差（Relative error）和平均相对误差（Mean relative error）两个性能指标来对预测模型的性能进行评价。

六合水库日水位预测，选取六合水库1995年之后的共4018条日水位数据来验证预测模型。原始时间序列如图4所示。

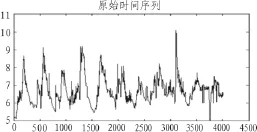
图4　原始时间序列Fig.4　The original time series

图5　重构后高频和低频信号Fig.5　The reconstructed high frequency and low frequency signal

前3978条水位数据被选取作为训练数据，后40条水位数据被用作测试数据。PNN-AR模型、过程神经网络模型以及BP神经网络模型的预测结果如图6所示，其中过程神经网络的网络结构均为输入层节点为10，隐层节点为6，输出节点为1。实验结果如图6和表1所示。

图6　预测结果对比Fig.6　The results of prediction

表1　误差对比Tab.1　Error comparison

从图6和表1可以得出：PNN-AR的预测精度优于过程神经网络的预测精度，从而说明该方法比单独使用过程神经网络泛化能力较强，预测效果较好，能充分拟合低频和高频信息。

3　结束语

文中将小波变换[9-11]和过程神经网络应用于非平稳时间序列的预测。首先根据趋向性非平稳时间序列具有的非线性、波动性和确定性等3个特性，采用二进正交小波变换对原始时间序列分解和重构，分离出原始序列中的高频部分和低频部分；然后利用对平稳时间序列具有较好预测能力的统计推断建模，并结合过程神经网络，实现对均值具有非平稳特性的时间序列的精确预测。实验表明，该方法是这类非平稳时间序列的有效预测方法，对进一步解决实际工程问题具有良好的应用前景。

[1]熊沈蜀，周兆英.神经网络在动力学系统建模中的理论研究[J].清华大学学报:自然科学版，1998（8）:26-31.

[2]张坤，郁湧，李彤.基于小波和神经网络相结合的股票价格模型[J].计算机工程与设计，2009（23）:5496-5498.

[3]Zhang G P，Qi M.Neural Network Forecasting for Seasonal and Trend Time Series[J].European J of Operational Research，2005，160（2）:501-514.

[4]何新贵，梁久祯.过程神经网络的若干理论问题[J].中国工程科学，2000，2（12）:40-44.

[5]许少华，何新贵.基于函数正交基展开的过程神经网络学习算法[J].计算机学报，2004，27（5）:645-650.

[6]何新贵，许少华.输入输出均为时变函数的过程神经网络及应用[J].软件学报，2003，14（4）:164-169.

[7]许少华，何新贵，李盼池.一类用于连续过程逼近的过程神经元网络及其应用[J].信息与控制，2004，33（1）:116-119.

[8]张晗，王霞.基于小波分解的网络流量时间序列建模与预测[J].计算机应用研究，2012（8）:3134-3136.

[9]李欣.小波变换和模糊凸集投影相结合的图像复原方法研究[J].电子设计工程，2015（18）：182-184.

[10]郜宪锦.基于小波变换的MSK信号码速率盲估计[J].电子科技，2015（5）:140-142.

[11]赵德明.小波变换和曲波变换的图像边缘检测新算法[J].科技创新与应用，2015（13）:53.

Time series prediction model based on wavelet and process neural network

LIU Xiu-heng，LV Xin，QI Rong-zhi，LIU Xuan，MA Hong-xu
（College of Computer and Information，Hohai University，Nanjing 211100，China）

A time series prediction method based on AR and process neural network PPN-AR was proposed.By Binary orthogonal wavelet transform，the non-stationary time series were decomposed into a low frequency signal and several high frequency signals.The low frequency was predicted with process neural network，and the high frequency signals were predicted with auto-regression models.The prediction result of the original time series was the superimposition of the respective prediction.

mallat decomposition；non-stationary time series；process neural network；autoregressive；prediction

TN-9

A

1674－6236（2016）01-0009-03

2015-09-10稿件编号：201509079

国家自然科学基金面上项目 （61272543）；国家科技支撑计划 （2013BAB06B04）；中国华能集团公司总部科技项目（HNKJ13-H17-04）；江苏省自然科学基金（BK20130852）；江苏省博士后科研资助计划（1401001C）

刘修恒（1992—），男，安徽阜阳人，硕士研究生。研究方向：数据挖掘。