自适应的L1-L2范数正则化图像去噪方法
豆泽阳,毕翔,曹宝杰
(中国传媒大学理工学部理学院,北京,100024)
自适应的L1-L2范数正则化图像去噪方法
豆泽阳,毕翔,曹宝杰
(中国传媒大学理工学部理学院,北京,100024)
提出了一种自适应的L1-L2范数正则化图像去噪方法。相比传统的L1范数正则化与L2范数正则化,新方法有效消除了阶梯效应,同时较好的保持了图像边缘信息。为了提高计算效率,将Split Bregman算法框架应用到提出的模型中,有效的提升了收敛速率并减少了计算时间。实验结果与分析验证了L1-L2范数正则化模型在图像去噪效果与计算效率的有效性。
图像去噪;自适应;L1-L2 正则化;Split Bregman迭代
1 引言
图像去噪是一个重要的研究课题。噪声对于图像的输入、采集、处理都会产生较大的影响。去除噪声对于提高图像视觉质量,提供更精确的纹理细节信息有着重要意义。目前常用的图像去噪方法有L2范数正则化(Tikhonov正则化)去噪[1]与L1范数正则化(TV正则化)去噪[2],然而两种方法均有缺陷:L2范数正则化无法较好的恢复图像边缘[3],而L1范数正则化虽然可以保持边缘,但是会出现阶梯效应,使图像产生虚假边缘,视觉效果不真实[4]。 为了解决L1范数正则化带来的阶梯效应,台雪成[5]等人提出了使用四阶偏微分方程来处理图像。但四阶偏微分方程会过度平滑图像的边缘,使得图像看起来较为模糊;Blomgren[6]等人提出了使用三阶多项式插值将L1范数与L2范数结合在一起,组成一种新的自适应的L1-L2范数正则化项,然而在三次多项式插值模型在每次迭代中都要重新计算插值多项式的系数,拖慢了计算效率。
受Blomgren思想的启发,本文提出一种新的正则化项,将L2范数与L1范数这两种平滑性度量结合起来,吸收各自的优点,根据图像的局部特征,自动调整正则化项,使得在梯度模值较大的边缘区域采用可以保持图像边缘的L1范数正则化,而在梯度模值较小的光滑区域采用平滑性较好的L2范数正则化。为了加快求解速率,本文应用Split Bregman框架[7]对新的模型进行求解,缩短了计算时间,提高了算法的运行效率。
2 自适应L1-L2范数正则化
2.1三阶多项式插值L1-L2范数正则化
为了结合L1范数正则化与L2范数正则化的优点,Blomgren[6]在有界变差函数空间BV和Sobolev空间做“插值”,使得其可以根据图像的局部特征,自动调整正则化项,在梯度模值较大的边缘区域采用可以保持图像边缘的L1范数正则化,而在梯度模值较小的光滑区域采用平滑性较好的L2范数正则化。新的范数正则化项可以表示为:

(1)
函数p(s)有如下性质:
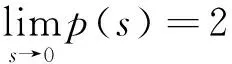

3. p(s)单调减
文献[8]表明,当p取定值且p∈[1,2]时,使用正则项R(u)均能得到较好的结果;当p增加时,恢复图像的阶梯效应在减弱。
三阶多项式插值L1-L2范数正则化基于三阶多项式插值的L1-L2范数正则化去噪模型为


(2)
其中,u0为被噪声污染的图像,λ为一个非负的常数,Gσ*u表示u与标准差为σ的高斯模糊核做卷积。函数p(s)具有以下形式:
(3)
其中e为图像梯度模值的最大值。在求解去噪模型(2)的过程中,由于图像梯度模值总在变化,所以每次迭代都需要重新计算p(s),增加了计算负担;p(s)的下降速度也难以控制。
求解模型(2)的传统的方法为直接算出泛函(2)的欧拉-拉格朗日方程,然后运用不动点迭代[6,9]求解,消耗时间较长,收敛较慢。
2.2改进的L1-L2范数正则化
本文将p(s)修改为:
(4)
k为非负常数。显然函数(4)满足2.1节中的三条性质。参数k 可以调节p(s)的形状。k值越小,函数图像越平缓,反之,函数图像越陡峭。图1表示了在不同的参数选择下,p(s)的函数图像。
Chambolle和P-L.Lions的研究[10]证明只有当p(s)=1 时,图像的边缘信息才能恢复,而式(4)不可能取到1。将(4)式做如下修改:
(5)


图1 不同参数选择p(s)的函数图像
3 Split Bregman方法
Split Bregman迭代方法由Goldstein和Osher[7]提出,是一种针对于L1范数正则项优化问题的快速算法。此算法的基本思路是通过引入对偶变量并借助增广拉格朗日法,将L1范数正则化问题转化为无约束优化问题,然后利用Bregman迭代将其分解为几个非常简单的子问题来求解。该算法大大简化了原问题的求解步骤,且具有快速收敛的特性。[11-14]本节将Split Bregman方法推广到非L1范数正则项优化问题。了将Split Bregman方法的框架应用到模型(2)中,引入一个对偶变量b并将▽u代替成b。模型(2)变为下列的有约束问题:
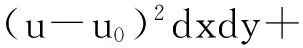

s.t. b=▽u
(6)
运用增广拉格朗日法,泛函(6)变为下列无约束问题:
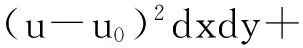


(7)
式(7)中γ为一个正常数,控制着惩罚项的权重。类似于Split Bregman迭代,提出以下Split Bregman 迭代格式:
(8)
显然,泛函(8)可以用交替迭代极小化框架求解:
3.1 固定b,解关于u的子问题
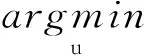
λ∬|bi|p(|▽(G*u)|)dxdy +
γ∬|bi-▽u-ti|2dxdy
(9)
推导出泛函(9)的欧拉-拉格朗日方程并令其为0,得到如下方程:
u-u0+γ▽·(bi-ti)-Δu=0
(10)
式(10)中Δ 为拉普拉斯算子。此方程可以用Gauss-Seidel迭代[15]快速求解。
3.2固定u,解关于b的子问题
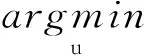


(11)
令b=(b1,b2),▽u=(ux,uy),t=(t1,t2),推导出泛函(11)的欧拉-拉格朗日方程并令其为0,得到如下方程组:
(12)
方程组(12)是一个非线性方程组,无法得到精确解。我们采用牛顿法来估计方程组(12)的解。由方程组(12)可以导出如下关系式:
(13)
将式(13)代入方程组(12),得到
(14)
其中
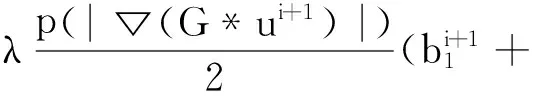
(15)
方程组(14)可以用牛顿法求解。为了保证牛顿法的收敛性,在使用牛顿法求解时,将bi+1的初值设为▽ui+1。
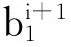
3.更新t :ti+1=ti+▽ui+1-bi+1。(16)
算法的实现步骤为:
(1)初始化:u0=u0,b0=t0=0;
(2)固定bi,解u的子问题(9);
(3)固定ui+1,解b 的子问题(11);
(4)用式(16)更新t;
(5)重复过程(2)、(3)、(4),直至算法收敛,迭代停止。
4 实验结果与分析

图2与图3为几种去噪方法对含有均值为0,方差为0.01的高斯噪声的图像去噪效果比较,(a)为原始图像,(b)为加噪声的图像,(c)为L1范数正则化模型的去噪效果,(d)为四阶偏微分去噪模型的去噪效果,(e)为L2范数正则化模型的去噪效果,(f)为本文模型的去噪效果。从图2和图3中可以看出,L1范数正则化虽然边缘保持的较好,但是有明显的阶梯效应;四阶偏微分去噪虽然没有阶梯效应,但是去噪效果并不理想,有小的斑点存在;L2范数也没有阶梯效应,但是图像边缘较为模糊;本文提出的新模型既没有阶梯效应,图像边缘也保持的较好。表1列出了用不同方法得出的去噪图像的信噪比。从表1中可以看出,对于合成图像而言,本文方法的信噪比最高,而对含有大量纹理的图像而言,本文方法的信噪比优于四阶偏微分方程模型和L2范数正则化模型而低于L1范数正则化模型,但信噪比只从一个侧面反映了处理结果的优劣,从图3(f)效果看,本文方法优于L1范数正则化模型,在明显减小了阶梯效应的同时,很好的保持了图像的边缘。

表1 各种模型的信噪比比较
表2列出了本文算法与Blomgren的三阶多项式插值L1-L2范数正则化对合成图像与Lena图像去噪的运算时间与迭代步数。从表中可以看出,本文算法的运算效率与传统的不动点迭代相比明显提高,计算时间明显减少,且收敛速率加快。

表2 迭代步数与计算时间时间比较

(a)原图 (b)噪声图

(c)L1范数正则化 (d)四阶偏微分

(e)L2范数正则化 (f)本文方法图2 不同方法对合成图像高斯噪声去噪比较

(a)原图 (b)噪声图

(c)L1范数正则化 (d)四阶偏微分

(e)L2范数正则化 (f)本文方法图3 不同方法对Lena图像高斯噪声去噪比较
5 结论
本文提出了一种自适应的L1-L2范数正则化图像去噪模型。该模型结合了L1范数正则化与L2范数正则化的优点,去除了阶梯效应,同时较好的保持了边缘。应用了Split Bregman迭代框架求解模型,计算效率明显增加。最后的实验结果表明,本文方法比现有的经典方法更有效。
[1]Voguel C. Computational Methods for Inverse Problems[M]. Siam,2002.
[2]Rudin L I,Osher S,Fatemi E. Nonlinear total variation based noise removal algorithms[J]. Physica D Nonlinear Phenomena,1992,60(1-4):259-268.
[3]查志远,刘辉,尚振宏,李润鑫. 基于1/2l范数正则化的图像重建方法[J/OL]. 计算机工程与应用,http://www.cnki.net/kcms/detail/11.2127.TP.20150605.1103.014.html
[4]You,Y L,Kaveh M. Fourth-order partial differential equations for noise removal.[J]. IEEE Trans Image Process,2000,9(10):1723-1730.
[5]Lysaker M,Lundervold A,Tai X C. Noise removal using fourth-order partial differential equation with applications to medical magnetic resonance images in space and time[J]. IEEE Transactions on Image Processing,2003,12(12):1579-1590.
[6]Blomgren P,Chan T F,Mulet P,et al. Total variation image restoration:numerical methods and extensions[J]. Proc IEEE Icip,1997,3:384-387.
[7]Goldstein T,Osher S. The Split Bregman Method for L1-Regularized Problems[J]. Siam Journal on Imaging Sciences,2009,2(2):323-343.
[8]Peter Blomgren,Pep Mulet,Tony F Chan. Extensions to Total Variation Denoising[C].Optical Scieucs,Engineering and Instrumentation’97 International Society for Optics and photonics,1997:367-375.
[9]Vitti A.The Mumford-Shah variational model for image segmentation:An overview of the theory,implementation and use[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2012,69:50-64.
[10]Chambolle A,Lions P L. Image recovery via total variation minimization and related problems[J]. Numerishce Mathematik,1997,76(2):167-188.
[11]Liu X,Huang L. Split Bregman iteration algorithm for total bounded variation regularization based image deblurring [J]. Journal of Mathematical Analysis & Applications,2010,372(2):486-495.
[12]Setzer S,Steidl G,Teuber T. Deblurring poissonian images by split bregman techniques[J]. Journal of Visual Communication & Image Representation,2010,21(3):193-199.
[13]Li M. A fast algorithm for color image enhancement with total variation regularization[J]. Sciece China Information Sciences,2010,53(9):1913-1916.
[14]Cai J F,Osher S,Shen Z,et al. Split Bregman Methods and Frame Based Image Restoration Multiscale Model[J]. Simul,2009,8(2):337--369.
[15]Tai X,Lie K,Chan T,Osher S.Image Processing Based on Partial Differential Equations[C]. Proceedings of the International Conference on PDF-Based Image Processing and Related Inverse Problens,CMA,Oslo,August 8-12,2005.
(责任编辑:王谦)
Adaptive L1-L2 Norm Regularization Method for Image Denoising
DOU Ze-yang,BI Xiang,CAO Bao-jie
(School of Science,Communication University of China,Beijing 100024,China)
An adaptive L1-L2 norm regularization method for image denoising is proposed. Compared to the traditional L1 norm regularization and L2 norm regularization,the proposed method removes the staircase effect effectively and maintains the edge information of the image. In order to improve the computation efficiency,the Split Bregman algorithm is applied to the proposed model,which effectively improves the convergence rate and reduces the computation time. Experimental results and analysis verify the effectiveness of the L1-L2 norm regularization model in the image denoising effect and the computational efficiency.
image denoising;adaptive norm;L1-L2 regularization;split Bregman iteration
2015-06-02
豆泽阳(1989-),男(汉族),河北省邯郸人,中国传媒大学硕士研究生.E-mail:douzeyang@cuc.edu.cn
TP391.41
A
1673-4793(2016)01-0050-06

