复数阶累加运算及其在广义复GM(1，1)中的应用

吴正鹏，刘永菲

(中国传媒大学 理学院，北京 100024)



复数阶累加运算及其在广义复GM(1，1)中的应用

吴正鹏，刘永菲

(中国传媒大学 理学院，北京 100024)

本文考虑复数阶累加运算，从理论上证明了将所有复数阶累加运算看成一个集合，在集合上定义类似于普通数的加法运算，其为交换群. 同时讨论了将所有实数阶累加运算看成所有复数阶累加运算的一个子集，其为一交换子群.并可以在其上定义商群.分析表明先对原序列进行m阶累加，在新得到的序列中再进行l阶累加，等价于对原序列进行m+l阶累加.结果表明对原序列先进行m阶累加，然后再进行-m阶累加，序列就回到原始序列，同时s阶累减运算可看成-s阶累加运算，最后将分析结果用于广义复GM(1，1)模型中，并进行误差分析。

复数阶累加；广义复GM(1，1)；误差分析

1　引言

邓聚龙教授曾对GM(1，1)作了十分深入的研究，得到了GM(1，1)模型的多种不同形式，并称之为GM(1，1)派生模型[1]，随后众多学者对其进行了补充和完善，文献[2]中详细列举了GM(1，1)模型的8种形式。文献[3]详细研究了GM(l，1)模型的适用范围和拟合误差，以及发展系数和拟合误差之间的关系。众多学者从模型背景值，初始条件，级比条件等角度研究了改进模型的拟合误差与预测精度问题[4-8]。 刘军等学者[9]基于单增序列比较论证不同GM(1，1)模型解间的相对误差，证明相对误差一致上界与序列长度和发展系数相关，提供白化模型解代替内涵解时发展系数需满足的条件。 二十世纪七十年代以来，研究人员发现分数阶微积分可以作为一种很好的描述与刻画手段，应用于分形几何、幂律现象与记忆过程等相关现象或过程。文献[9，10]将矩阵生成技术应用到灰色建模中，提出灰建模的累加生成矩阵和还原矩阵。吴立峰等学者[11]在此基础上提出分数阶累加生成，并应用到灰色模型中，提出分数阶累加GM(1，1)。

本文基于上述学者研究，考虑复数阶累加运算，从理论上证明了将所有复数阶累加运算看成一个集合，在集合上定义类似于普通数的加法运算后，其为一交换群。 同时讨论了将所有实数阶累加运算看成所有复数阶累加运算一个子集，其为一子交换群。尤其可以在其上定义商群。分析表明先对原序列进行m阶累加，在新得到的序列中再进行l阶累加，等价于对原序列进行m+l阶累加。当m=-l时，即对原序列先进行m阶累加，然后再进行-m阶累加，序列就回到原始序列，同时s阶累减运算可看成-s阶累加运算，最后将分析结果用于广义复GM(1，1)模型中。

2　复数阶累加生成算子

针对原始序列

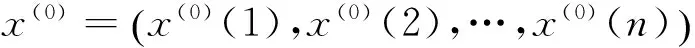
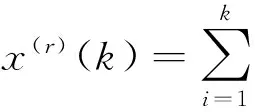
x(r)=Ax(r-1)=AAx(r-2)=A2x(r-2)=…=Arx(0)

其中A为一次累加生成矩阵

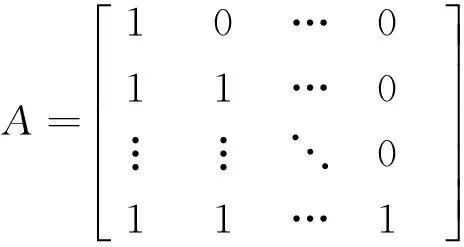
这样，我们可以得到

(1)

基于式(1)，结合组合数的推广，考虑将r由整数推广到复数，可以得到复数阶累加生成矩阵。

定理1针对如式(1)所示的累加生成，先对原序列进行m阶累加，在新得到的序列中再进行l阶累加，等价于对原序列进行m+l阶累加。

证明：由定义1可知

根据矩阵的乘法可知

又由定义1可得

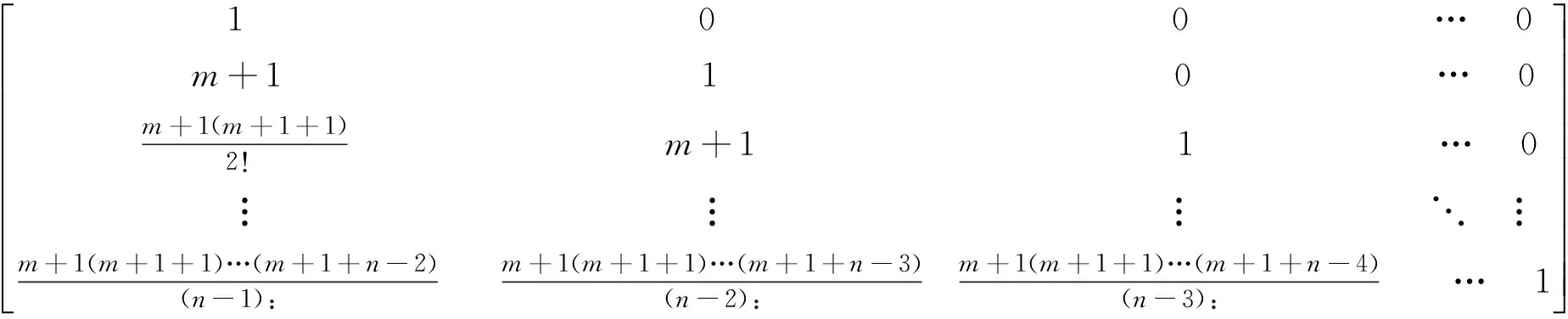
故有Am·=Am+1。所以x(0)A1=Am+1结论成立。

定理2将所有复数阶累加运算看成一个集合，在该集合上定义如上的运算，为一交换群，用符号Α表示

证明：

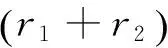
(2)对原序列不做任何阶累加称为原序列的0阶累加，显然0阶累加即为Α的单位元。

(3)对原序列进行r阶累加，在新得到的序列中再进行-r阶累加，则回到原序列，即。故-r为r的逆元。

又因为对A中的元素r1，r2，先对原序列进行r1阶累加，在新得到的序列中再进行r2阶累加，等价于先对原序列进行r2阶累加。再在新得到的序列中进行r1阶累加。即故运算的交换律成立。

因此Α为交换群。

综上所述，先对原序列进行m阶累加，在新得到的序列中再进行l阶累加，等价于对原序列进行m+l阶累加。当m=-l时，即对原序列先进行m阶累加，然后再进行-m阶累加，序列就回到原始序列，同时s阶累减运算可看成-s阶累加运算。即没有累减运算。

2　复数阶累加生成算子

对于原始数据序列x(0)={x(0)(1)，x(0)(2)，…，x(0)(n)}，称x(r)={x(r)(1)，x(r)(2)，…，x(r)(n)}为r次累加生成序列，其中x(r)=Arx(0)；称z(r)={z(r)(2)，z(r)(3)，…，z(r)(n)}为均值生成序列，其中z(r)(k)=0.5x(r)(k-1)+0.5x(r)(k)，下面给出如下定义。

定义 2称

x(r-1)(k)+az(r)(k)=b

(2)

为复数阶累加灰模型GM(1，1)的定义型，其中k=2，3，…，n，记为CAGM(1，1，D)模型。并称a为模型发展系数；b为模型背景值。

定义 3称微分方程

为复数阶累加灰色模型白化微分方程。

结合初始条件x(r)(1)=x(0)(1)可得到方程(3)的解为

(4)

由(4)可以得到(2)的还原值。

定义 4称(2)和(4)为复数阶累加灰色模型白化型，记为CAGM(1，1)模型。 CAGM(1，1)模型实际上可看作是GM(1，1)模型在累加生成阶数上的一种推广，当累加生成阶数r=1+0*i时，CAGM(1，1)模型即为GM(1，1)模型。

建模步骤如下：

(1)原始序列计算得到r阶累加序列，；

(2)将生成累加序列的实部和虚部分别进行建模，用最小二乘法估计参数；

(3)根据模型求累加序列的模拟值及模型还原值

(4)检验误差

3　实例分析

实例1

下面本文以2008-2012全社会固定资产投资为例，建立基于复数阶累加的CAGM(1，1)模型，分析模拟结果，并对2013年数据进行预测，与真实值进行了比较预测精度。

例题1以2008年—2012年全国居民消费价格指数为例，建立了累加生成阶数为1阶，1+0.01*i阶，1-0.000001*i阶以及0.99阶，0.99+0.01*i阶，0.99-0.000001*i阶的CAGM(1，1，D)模型，其中a表示模型的发展系数，b表示背景值，Δ表示平均相对误差。

由表1 可以发现：

(1)从模拟精度来看，累加阶数为0.99、0.99+0.01*i、0.99-0.000001*i时，其模型的相对误差明显小于累加阶数为1、1+0.01*i、1-0.000001*i时；累加阶数为1时模型的模拟精度小于累加阶数为0.99时；

(2)从预测效果来看，累加阶数为0.99、0.99+0.01*i、0.99-0.000001*i时的预测效果明显好于累加阶数为1、1+0.01*i、1-0.000001*i时；累加阶数为0.99时模型的预测效果明显好于累加阶数为1时；

表1　全社会固定资产投资预测模型

说明：在二维平面中，1+0.01*i，1-0.000001*i都可视为距离与1+0*i很近的点，故在进行建模过程中，可以进行1阶灰色系统建模的数据在进行1+0.01*i阶，1-0.000001*i阶累加后亦满足指数分布，可将实部和虚部分别带入(2)、(3)、(4)进行建模。

综合来看累加阶数为0.99阶，0.99+0.01*i阶，0.99-0.000001*i阶的模拟和预测精度较高，其中，累加阶数为0.99时最高，0.99-0.000001*i次之，相对而言，模拟精度和预测精度较低的是1阶和1-0.000001*i阶。此结果表明复数阶累加在一定情况下可以提高预测和模拟精度，拟合效果要优于整数阶累加。

实例2

下面本文以全国生产故事影片(部)为例，以2007-2011年数据建立基于复数阶累加的CAGM(1，1)模型，并对2012年影片进行预测，最终对模拟及预测结果进行对比分析。

表2中以2007年—20011年全国生产故事影片数据为例，建立了累加生成阶数为1阶阶以及

阶的模型并对2012年故事影片数进行预测，其中表示模型的发展系数，表示背景值，表示平均相对误差。

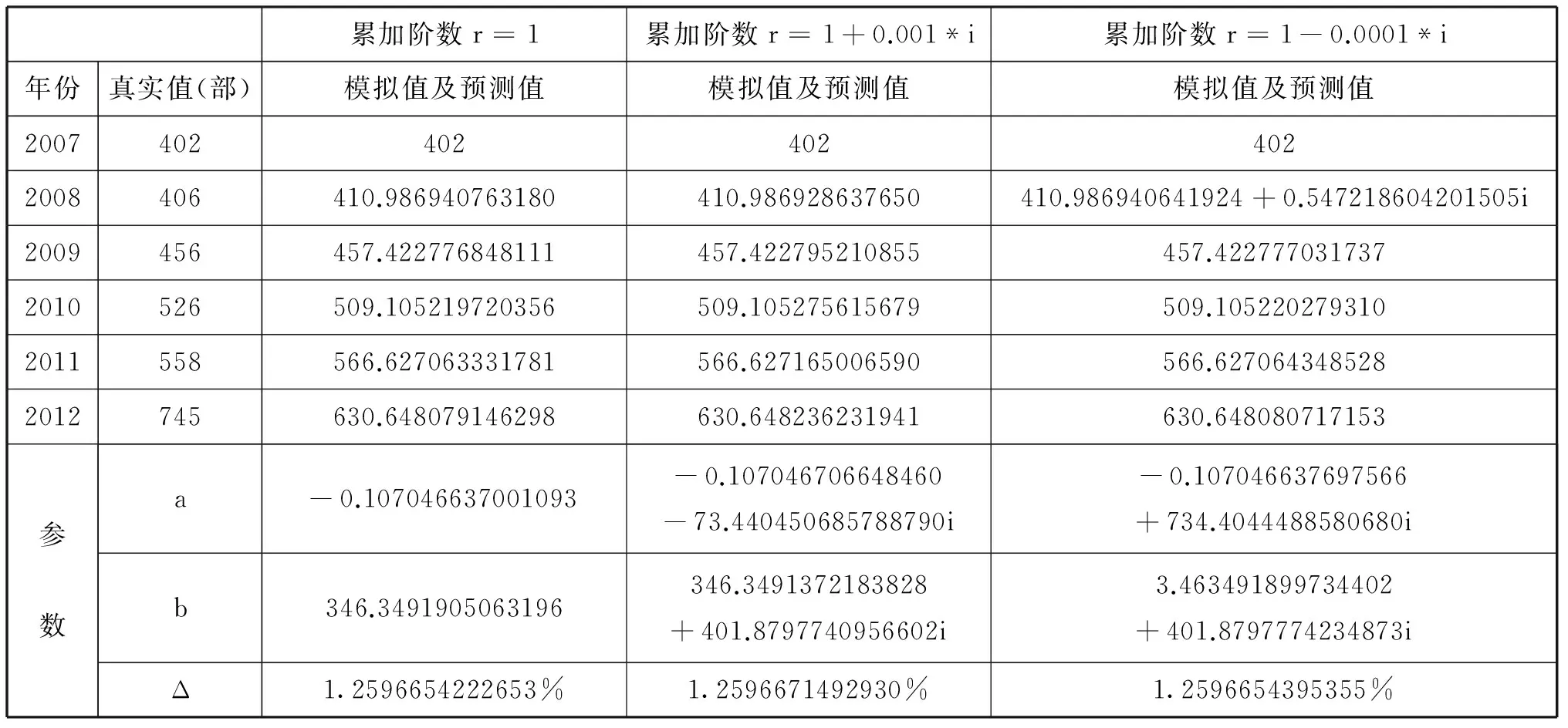
表2　全国生产故事影片预测模型

通过表2可以发现：

(1)就模拟精度来看，累加阶数为1时的模拟精度稍高于及阶时；

(2)就预测精度而言，累加阶数为时的预测精度要稍高于时。

此结果表明复数阶累加在一定情况下的预测效果要优于整数阶累加，但拟合精度稍差于整数阶累加。

4　结论

本文考虑复数阶累加运算，将所有复数阶累加运算看成一个集合，在集合上定义类似于普通数的加法运算后，其为交换群。同时讨论了将所有实数阶累加运算看成所有复数阶累加运算一个子集，其为一子群，并可以在其上定义商群。分析表明先对原序列进行m阶累加，在新得到的序列中再进行l阶累加，等价于对原序列进行m+l阶累加；对原序列先进行m阶累加，然后再进行-m阶累加，序列就回到原始序列。同时s阶累减运算可看成-s阶累加运算，从理论上证明了进行复数阶累加的可行性。最后将分析结果用于广义复GM(1，1)模型中，通过分析发现复数阶累加在一定情况下的拟合效果和预测结果并不比整数阶累加差，甚至要优于整数阶累加，至于在哪些情况下还需进行进一步的研究。

[1]邓聚龙. 灰理论基础[M]. 武汉：华中科技大学出版社，2002.

[2]肖新平，毛树华. 灰预测与决策方法[M]. 北京：科学出版社，2013.

[3]刘思峰，党耀国，方志耕著.灰色系统理论及其应用[M]. 北京：科学出版社，2010.

[4]Xiao X P，Song Z M，Li F. The Foundation of Grey Technology and Its Application [M]. Beijing：Science Press，2005.

[5]Kang X Q，Wei Y. A New Optimized Method of Non-EquigapGM(1，1)Model[J]. The Journal of Grey System，2008，20(4)：375-382.

[6]Xie N M，Liu S F. Discrete grey forecasting model and its optimization[J]. Applied Mathematical Modelling，2009，33：1173-1186.

[7]Wang Y H，Dang Y G，Li Y Q，et al. An approach to increase prediction precision of GM(1，1)model based on optimization of the initial condition[J]. Expert Systems with Applications，2010，37(8)：5640-5644.

[8]周伟，方志耕，刘思峰.基于级比优化的广义GM(1，1)预测模型[J].系统工程理论与实践，2010，30(8)：1433-1438.

[9]刘军，肖新平，郭金海. 单增序列灰色GM(1，1)模型解之间的误差分析[J]. 系统工程理论与实践(录用待刊).

[10]肖新平，宋中民，李峰. 灰技术基础及其应用[M].北京：科学出版社，2005.

[11]Lifeng Wu，Sifeng Liu，Ligen Yao，Shuli Yan，Dinglin Liu. Grey system model with the fractional order accumulation[J]. Communications in Nonlinear Science and Numerical Simulation，2013，18(7)：1775-1785.

[12]杨子胥.近世代数[M].北京：高等教育出版社，2003.

(责任编辑：马玉凤)

Complex Order Accumulation and Its Use in Generalized Plural GM(1，1)

WU zheng-peng，LIU Yong-fei

(School of Science，Communication University of China，Beijing 100024)

Based on the definition of complex order accumulation，this paper has many interesting results. First，all of complex order accumulations is a commutative group，and real order accumulations is a subgroup，according to ordinary addition of number and number-multiply. By themorder accumulation of raw data and thenlorder accumulation，it is the same as them+lorder accumulation. asmis equal to-m，it went back to its original sequence. The accumulation ofsorder is the same as the inverse accumulation of-sorder. At last，it was used in discrete GM(1，1)model.

complex order accumulation；discrete GM(1，1)；error analysis

2015-07-06

吴正鹏(1966-)，男(汉族)，安徽省庐江县人，副教授，博士.E-mail：wuzhengpeng@126. com

N941

A

1673-4793(2016)01-0006-07