I型超导体全离散T-ψ有限元法的误差估计
韩青青,陈涛,康彤,王然
(中国传媒大学信息工程学院,北京100024)
I型超导体全离散T-ψ有限元法的误差估计
韩青青,陈涛,康彤,王然
(中国传媒大学信息工程学院,北京100024)
采用将磁场H进行T-ψ有限元分解的方法来解决I型超导的问题,其中带有奇异核的卷积项是误差估计的关键.首先我们要给出T-ψ具体形式,以及变分形式和相关的函数空间;其次,给出全离散格式,并证明其变分问题解的存在唯一性;最后,进行稳定性研究和误差估计。
I型超导体;奇异;全离散T-ψ方法;误差估计
1 引言
为了给出本文要研究的数学模型,先从简化的麦克斯韦方程组入手
(1)
其中B表示磁通量,E表示电场,H表示磁场,J表示电流密度。
.接下来定义Hilbert空间

H(curl,c):={v∈L2(c):▽×v∈L2(c)}
H0(curl,c):={v∈H(curl,c):v×n=0on∂c}

((P,φ),(Q,φ))v:=(P,Q)H1(c)+(▽φ,▽φ)Lz()

在本节我们将给出几个重要的估计式.

(1.2)
(k0★h1,▽×h2)≤Cε‖h1‖2+ε‖▽×h2‖2,∀h1∈L2(),h2∈H0(curl,)
(1.3)
定义1.1对于所有的(Q,φ)∈V存在(T,ψ)∈H1((0,T),V),使得下式成立
(1.4)
2 全离散
设Th是标准四面体剖分,下面我们定义有限元空间


全离散解的存在唯一性用Lax-Milgram定理容易得到.下面定义分片插值函数
因此(2.1)式的弱形式如下

=0∀(Qh,φh)∈Vh
(2.2)
3 稳定性和误差估计
定理 3.1对于j=1,2,…,n,存在两个常数τ0和C,使对于任意的0<τ<τ0,有

定理3.2设(1.4)的弱解(T,ψ)和初值(T0,ψ0)满足
(T,ψ)∈L2((0,T),H2(C)×H2()),(T0,ψ0)∈H1(C)×H2()
则全离散问题满足如下的误差估计
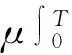




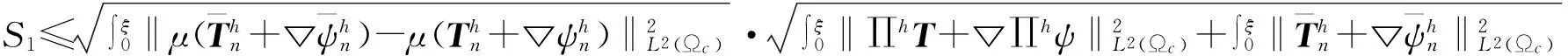









合并整理,运用Gronwall不等式,定理得证。


4 结论
本文通过将磁场H进行T-φ有限元分解,以及之后的误差估计和稳定性研究,从理论上证明了T-φ有限元方法解决Ⅰ型超导问题的可行性。
[1]Odeh F M.On the integrodifferential equations of the nonlocal theory of superconductivity[J].J Math Phys,1964,(8):1168-1182.
[2]Lin T,Rogers R C. Accurate computation of the field in Pippard’s nonlocal superconductivitymodel[J].Integral Equations Appl,1995,7(2):167-192.
[3]Zienkiewicz O C.Finite element-the basic concepts and the application to 3D magnetostatic problems[M].London:John Wiley & Sons INC,1980.
[4]Slodicka M.Nonlinear diffusion in type-II superconductors[J].J Computational & Applied Mathematics,2008,215(2):568-576.
[5]Monk P.Finite Element Methods for Maxwelll’s Equations[M].UK:Oxford Seience Publications,2003.
(责任编辑:王谦)
Error Estimate of A Fully DiscreteT-ψfinite Element Method for Type-superconductor
HAN Qing-qing,CHEN Tao,KANG Tong,WANG Ran
(School of Sciences,Communication University of China,Beijing 100024,China)
This paper is devoted to the study of a fully discreteT-ψfinite element method based on H-decomposition to solve a nonlocal parabolic model for Type-I super-conductors. We first design a nonlocal scheme for approximation in suitablefunction spaces. Then,we suggest a fully discrete scheme and prove the convergence of the nonlocal scheme. Finally,derive itserror estimate.
type-I superconductor;singular;fully discreteT-ψfinite element method;error estimates
2015-07-14
韩青青(1990-),女(汉族),山西晋中人,中国传媒大学硕士研究生.E-mail:1244919106@qq.com
O241.82
A
1673-4793(2016)01-0056-05

