张量CP分解、半正定张量和范德蒙张量

徐常青，祁力群

（1.苏州科技大学 数理学院，江苏 苏州215009；2.香港理工大学 应用数学系，中国 香港999077）

张量CP分解、半正定张量和范德蒙张量

徐常青1，祁力群2

（1.苏州科技大学 数理学院，江苏 苏州215009；2.香港理工大学 应用数学系，中国 香港999077）

张量，又称超矩阵，是矩阵的高阶推广。首先介绍张量基本概念（包括张量的特征值和张量的行列式等）和张量的基本运算（主要是张量乘积），重点介绍张量秩-1分解、半正定张量、Hankel张量和Vandermonde张量的最新研究进展。

张量；张量分解；Hankel张量；Vandermonde张量；半正定张量

1 张量的基本理论

张量首先作为一个物理量出现在相对论、流体力学、动力学和电磁学等应用领域。作为一个数学名词，它是19世纪由Gauss、Riemann和Christoffel等人在研究微分几何学时提出；20世纪初，Ricci，Levi-Civita等人将张量分析发展成一个数学分支。1916年，爱因斯坦应用张量研究并提出划时代的广义相对论，使张量分析成为研究理论物理、力学及其他学科的重要工具。1927年，Hitchcock开始研究高阶张量的秩-1分解［1］，1966年，Tucker对3阶张量秩-1分解进行了系统研究［2］，1970年，Harshman称张量秩-1分解为PARAFAC分解，并用张量给出统计学中的多因子分析模型及模型求解方法［3］。关于对称张量特别是半正定张量谱性质及其秩-1分解研究主要来自于祁力群和 L.H.Lim从2005年至2010年期间的研究工作［4-11］，而特殊结构张量如Hankel张量、Cauchy张量、Hilbert张量、B-张量和M-张量是近几年才开始被人们所关注和研究［9，12-16］；具非负性张量如完全正张量（completely positive tensor）、全正张量（totally positive tensor）和协正张量（copositive tensor）研究起始于2014年［8-9，14］，关于元素非负张量研究的关键突破来自于2008年张恭庆院士等人将Perron-Frobenius定理推广至非负张量方面的系列结果［17］。

一个m阶张量A是一个有m个方向（或维度）的数组，A的每个元通过m个下标索引来确定其位置。如一个数为0阶张量，一个向量为1阶张量，而矩阵为2阶张量。物理和力学研究中的一个关键概念是与其张量有关的不变量，即不随参照系改变的物理量或几何量。如向量作为1阶张量，它的一个不变量为其长度或模，而2阶张量——矩阵的特征值（奇异值）为其主要不变量。

记n维实向量空间为Rn，Rm×n为由m×n实矩阵构成的线性空间，它同构于一个n维实向量空间V到一个m维实向量空间U的全体线性变换构成的集合。类似，一个4阶张量A∈Rn1×n2×n3×n4可视为Rn1×n2到Rn3×n4的线性变换（ni为任意正整数）。一般，记一个大小I1×I2×…×Im的m阶张量A为其中A在第i维度（i-way）对应的维数（dimension）为ni。当m＞2时，A称为一个高阶张量（或超矩阵）。若I1= I2=…=Im＝n，则称A为m阶n维张量（m阶超立方体）。全体m阶n维实张量构成的集合记为Tm；n。A在第k方向的第i个切片 （A）定义为固定A的第k个下标ik=i后得到的m-1阶张量。注意（1）式中的A在k-方向有Ik个切片。

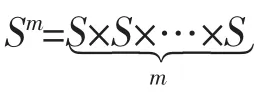
物理中出现的张量多数情况下被理解为一个物理量，而几何意义下的张量一般为一个Hilbert空间H中的一个多重线性函数，在固定H的一个标准正交基后，该函数表现为一个超矩阵。形如

（3）式称为A的一个秩－1分解。张量秩－1分解一般不唯一。A的秩为其所有秩－1分解（3）式中最小可能的项数K。记 rankR（A）为A在实数域上的秩，即A存在（3）式分解，其中向量均为实向量。

注意到，一个p×q实阵A一定满足rank（A）≤min（p，q），且rank（A）不依赖于数域，但高阶张量则不然。如下面的例子。

例1 考虑2×2×2张量A

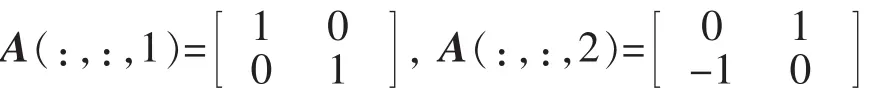
可以证明，它在实数域R上的一个最小秩－1分解为A＝x（1）×x（2）×x（3）+y（1）×y（2）×y（3）+z（1）×z（2）×z（3），其中

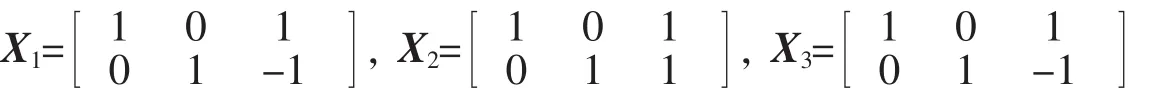
Xi=［x（i），y（i），z（i）］。可证A不存在K＜2的秩－1分解。由于K≥rank（A（：，：，j）），故只需证明A不存在K=2的秩－1分解。事实上，若A存在秩－1分解，A＝α1×β1×γ1+α2×β2×γ2，αi，βi，γi≠0。记γi＝（xi，yi）T，i=1，2，那么有xi≠0，yi≠0（i=1，2）且

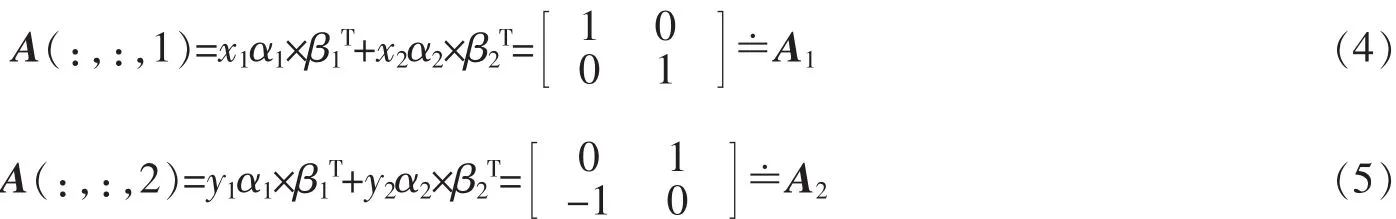
由（4）式知，［β1，β2］－T＝［x1α1，x2α2］，代入（5）式，得

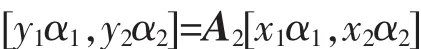
因此，有A2α1＝λ1α1，A2α2＝λ2α2，其中λi＝yi/xi，i=1，2，但矩阵A2无实特征值，矛盾。因此 rankR（A）=3。而在复数域C上，有

定义 1 （1）式定义的张量 A与一个 Ik×J矩阵 P沿方向 k的乘积为 I1×…×Ik-1×J×Ik+1×…×Im张量G=（Gi1i2…im），它满足

记G=A×kP。类似，定义P与A的乘积P×kA为

（6）式可推广至任意两个张量A，B在任意相容维度（即A，B在该方向上维数一致）上的乘积。如一个m×n×p张量A与m×n张量（矩阵）P沿｛1，2｝-维度乘积A×｛1，2｝P为向量v=（v1，…，vp）T

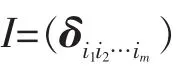
定义2 对任意n维实向量v=（v1，…，vn）T，记vm=（vi1i2…im）∈Tm；n为一个m阶秩1张量，它在每个维度上的维数均为n（这样的张量又称为k阶n维张量或超立方体），其元定义为

由（8）式定义的向量为由向量v确定的一个k阶秩1对称张量。给定一个n维向量x，x的支撑集supp（x）定义为x的所有非零分量对应的指标集，即supp（x）=｛i：xi≠0，1≤i≤n｝。

下面介绍正定张量、半正定张量及其分解。

2 张量的正定及其分解

正定张量由祁力群于2005年定义［4］，它在医学CT成像等领域有重要应用［8］。为了定义（半）正定张量，先来定义对称张量和一个m阶n维张量A对应的m次齐次多项式。

定义3 m阶n维张量A＝（Ai1i2…im）称为对称张量，若其元素下标任意排列后不改变元素大小。全体对称张量一定是超立方体，它为对称矩阵的高阶推广。记全体m阶n维超立方体构成的集合为STm；n。

对称张量的任意切片均为对称张量［17］，3阶张量A＝（Aijk）∈Rn×n×n在3个方向上的每个切片均为n阶对称矩阵。依照张量乘积定义，可定义张量（超立方体）A确定的多项式。

定义4 给定向量x∈Rn和m阶n维张量A＝（Ai1i2…im）。A与对称张量xm的乘积定义为

这里S（m，n）=｛（i1，…，im）：1≤ik≤n｝为A的所有元下标构成的集合。（9）式为A和张量xm的内积。记Hm［x1，…，xn］为实数域向量x＝（x1，…，xn）T确定的全体n元m次齐次多项式构成的集合（含零多项式）。那么

引理1 Hm（x1，…，xn）≌STm；n。

证明 先证明：若一个对称张量A∈STm；n满足

那么A=0（即A的每个元为零）。考虑任意的τ=（i1，…，im）∈S（m，n）。由A的对称性，不妨假设1≤i1≤…≤im≤n。下面证明Aτ＝Ai1i2…im＝0。称＜τ＞：=｛i1，…，im｝为τ的基集，t=|τ|：＝|＜τ＞|，即i1，…，im中两两不等的元素个数为t。不妨设

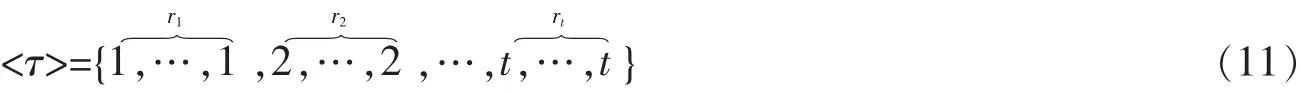
其中

取x∈Rn，使supp（x）=｛1，2，…，t｝。由（10）式，得

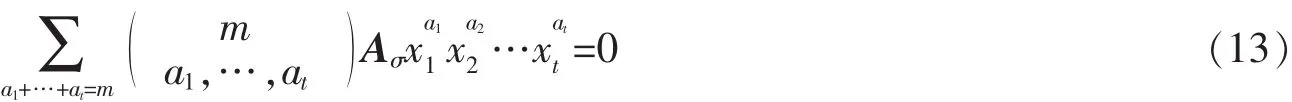
（13）式左边为一个关于t个变元x1，…，xt的多项式，对所有x1，…，xt其值为零，因此，该多项式系数均为零。所以∀σ=（i1，i2，…，im）∈S（m，n），Aσ=0，σ满足（11）和（12）式。故Aτ=Ai1i2…im=0。

现假设对称张量A，B∈STm；n满足条件Axm=Bxm（∀x∈Rn），则（A-B）xm=0，∀x∈Rn。从而由上述结论知A=B，从而结论得证。

引理1说明n元m次齐次多项式与m阶n维对称张量的一一对应关系。

定义5 一个对称张量A称为（半）正定张量，如果A满足

（半）正定张量为（半）正定矩阵推广。

推论1 一个非零（半）正定张量一定为偶数阶张量。

证明 设A为半正定张量。若m为奇数，则A（-x）m=-Axm。因此，有

由引理1的证明可知，A=0，与题设矛盾，故m为偶数。

由推论1知不存在非零正定（半正定）张量。因此，以下考虑偶数阶张量的正定性。注意到一个对称矩阵为正定（半正定）当且仅当其特征值全为正（非负）。为此，先来介绍张量的特征值。张量的特征值和特征向量由Qi［5］和Lim［18］在2005年定义：

定义6 设A∈Tm；n。若存在非零向量x∈Cn和数λ∈C，使得

若m=2，则A为一个n×n矩阵，由（16）式不难发现，（15）式定义的特征值、特征向量为矩阵通常意义下的特征值与特征向量。

定义7［18］设A∈Tm；n。若存在非零实向量x∈Rn和实数λ，使得

则称λ为A的一个Z-特征值，x为A对应于λ的Z-特征向量。

Qi［4］证明了下面的结论：

定理1 设A∈STm；n且m为偶数。 则A一定存在H-特征值和Z-特征值，且A为正定（半正定）张量当且仅当A的所有H-特征值（或Z-特征值）均为正数（非负数）。

与对称矩阵不同的是，一个对称张量的特征值不一定为实数。由定理1知，偶数阶对称张量一定存在实特征值（H-特征值），而判定一个对称张量是否正定（半正定）只需考察其所有H-特征值是否为正（非负）即可。这样，判定张量正定性问题就转化为求张量的最小H-特征值的正性即可。文献［13］给出了对称张量最小H-特征值（和Z-特征值）的一些可行（可计算）的上下界及用于改进这些界的算法，为正定张量的判定提供了可行的充分性依据。

3 张量的行列式

众所周知，一个n×n矩阵A的行列式 f（A）=det（A）为关于A的n2个元的连续函数，且f（A）关于A的列（行）向量具线性性，它可通过代数积和式、按行（列）展开或通过矩阵初等变换等方法进行计算，还可用于计算A的特征多项式，从而计算A的特征值等不变量。但一个高阶张量的行列式的定义要复杂得多。为了介绍张量行列式（尽管高阶张量行和列的概念已模糊，但张量行列式（determinant）的意义已不局限于此），首先介绍预解式（resultant），一个在数论中广泛应用的概念［19］。

定义8 设P（x），Q（x）∈C［x］为次数分别为p，q的首一多项式。P和Q的根集（即满足P（x）=0的解x构成的集合）分别记为SP=｛a1，…，ap｝和SQ=｛b1，…，bq｝。（P，Q）的预解式Res（P，Q）定义为

注意到一个多项式的根为关于其系数的函数，故Res（P，Q）可视为关于P和Q的系数的函数。记

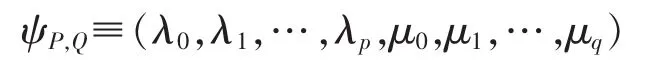
其中 P（x）=λ0xp+λ1xp-1+…+λp，Q（x）＝μ0xq+μ1xq-1+…+μq。 用多项式系数向量（次数递减）P=［λ0，λ1，…，λp］，Q＝［μ0，μ1，…，μq］代替P和Q，则Res（P，Q）为关于ψP，Q的函数，记

由（18）式，Res（P，Q）=0当且仅当P，Q有公共根。

预解式Res（P，Q）可通过Sylvester矩阵来定义［17］。特别，P的判别式Δ（P）定义为Res（P）=Res（P，P'），即P与其导函数的预解式。一元多项式P有重根当且仅当Δ（P）=0。而方阵A的行列式det（A）可用于判定方程组Ax=0非零解存在性或A的奇异性，因此，det（A）可视为判断A是否奇异的判别式。下面定义的对称张量的行列式可视为判别对称张量奇异性的判别式［19］。

定义9 设A=（ai1…im）∈STm；n。A的行列式f（A）≡det（A）为一个满足以下条件的齐次多项式：

（1）f（A）＝0⇔∃0≠x∈Cn，s.t.Axm-1=0；

（2）若A为单位张量，则f（A）=1；

（3）f（A）为关于nm元（ai1…im）的不可约多项式。

由文献［19］中第13章知，给定对称张量A，f（A）≡det（A）存在且唯一。作为ai1…im的整系数多项式，f有很多好的特性，如关于A的切片的对称性等，在此不再讨论。下面例子给出了一个2×2×2张量的行列式。

例2 设A＝（aijk）∈R2×2×2。A的行列式det（A）为

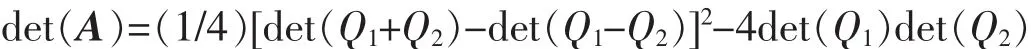
其中

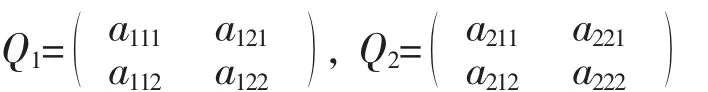
令X=A（：）∈R8。为方便，记Q1=［x11，x12；x21，x22］，Q2=［y11，y12；y21，y22］。则det（A）为一个8元4次齐次多项式。运用MATLAB符号计算，发现其展开式中共12项，即

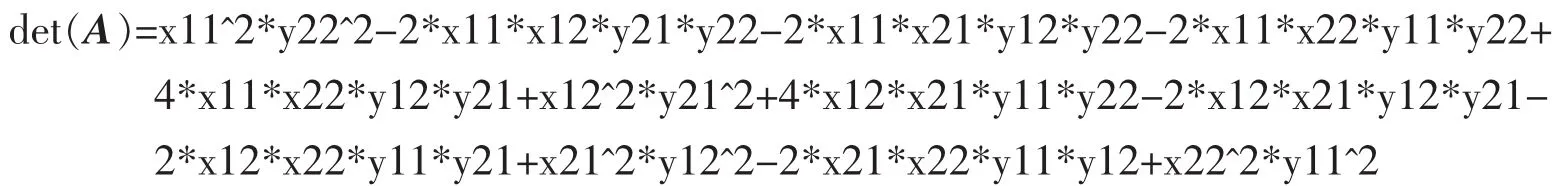
4 Hankel张量和Vandermonde张量

Hankel张量研究起源于2013年祁力群的工作［9］，而Vandermonde张量由笔者在文献［16］中首次提出。记x=（x1，…，xn）T，由x生成的n阶Vandermonde矩阵，简称V-矩阵，记为V=V（x）=（aij），满足

Vandermonde矩阵行列式（范德蒙行列式）由公式

给出。由（21）式可见，V为奇异矩阵当且仅当x有取值相等的分量。

若n=2k-1为奇数，则由x可定义一个k阶Hankel矩阵，H=H（x）=（hij），满足

注意到Hankel矩阵为对称矩阵，而V-矩阵一般为非对称矩阵。

现将这两类矩阵推广至张量情形。

定义10 给定n维向量x。由x确定的Vandermonde-张量（简称V-张量）由

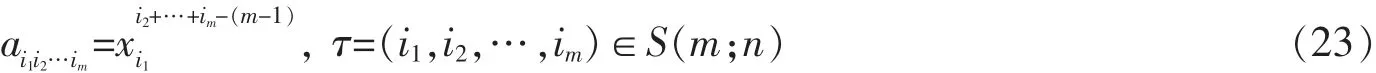
给出，其中

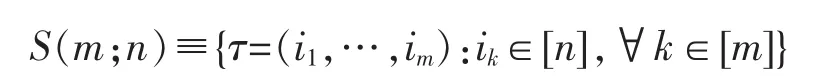
当m=2时，V-张量即范德蒙矩阵。因此，（23）式为（20）式的推广。

定义11 设n=2k-1为奇数且x∈Rn。x关联的m阶Hankel张量H=（hi1i2…im）由

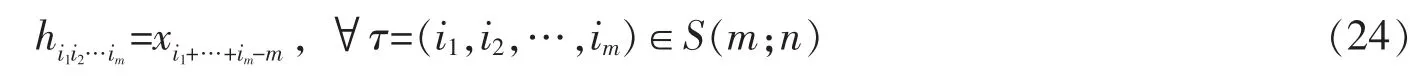
定义。

显然，一个2阶n维Hankel张量即为一个Hankel矩阵。

定义12 给定m阶张量A∈Tm；n。A沿方向k的一条纤维（fiber）是指通过固定除ik以外的所有下标is得到的一个n维列向量，即∀σ=（i1，…，ik-1，ik+1，…，iN）∈S（k）（I）

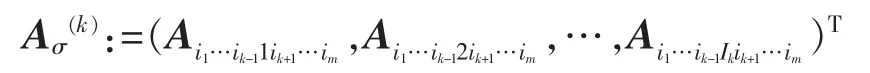
沿方向n的纤维有nm-1条。将这些纤维作为列向量按原有顺序排列，得大小为n×nm-1矩阵A（k），它称为张量A沿方向k经矩阵化后得到的矩阵。对A∈Rn×n×n，A的矩阵化后得

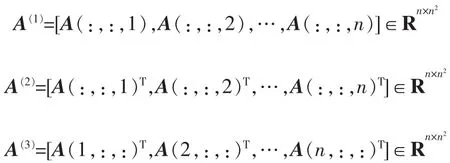
利用张量矩阵化，可计算高阶张量SVD分解（HOSVD），从而可对张量进行低秩逼近。在此略去有关高阶张量SVD的算法和原理，可参见文献［18］。文献［15］证明了以下结论：

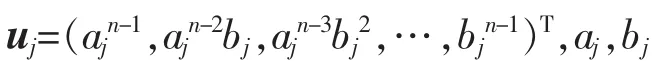
由（25）式，定义一个Hankel张量A的Hankel秩为A的所有形如（25）式的分解中最小可能的数N，记为hrank（A）=N。有关Hankel张量的研究，可参见文献［13，15］。

设x＝（x1，…，xn）T∈Rn。x称为是一个Noi-向量，若x满足以下两个条件：

（1）xk≠0，∀k∈［n］；

（2）∀i，j∈［n］，i≠j⇒xi≠xj。

文献［16］中证明了：

定理3 设x＝（x1，…，xn）T∈Rn，V为与x关联的V-矩阵，A是与x关联的V-张量。则A×1V为Hankel张量，且hrank（A×1V）≤n。进一步，hrank（A×1V）=n当且仅当x为一个Noi-向量。

形如（25）式的分解称为张量的Vandermonde分解（V-分解）。文献［12－13，15－16］中运用V-分解研究了Hankel张量，文献［15］还定义了强Hankel张量和完全Hankel张量。文献 ［16，20］中给出了Vandermonde张量、全正（Totally positive）张量的定义，研究了V-张量的基本性质，证明了一个Vandermonde张量一定为全正张量。

［1］HITCHCOCK F L.The expression of a tensor or polyadic as a sum of products［J］.J Math Phys，1927，6：164-189.

［2］TUCKER L R.Some mathematical notes on three-mode factor analysis［J］.Psychometrika，1966，31：279-311.

［3］HARSHMAN R A.Foundations of the PARAFAC procedure：Models and conditions for an explanatory multi-modal factor analysis［J］.UCLA Working Papers in Phonetics，1970，16：1-84.

［4］QI L.Eigenvalues of a supersymmetric tensor and positive definiteness of an even degree multivariate form［R］.Hong Kong：Depart of Applied Mathematics，The Hong Kong Polytechnic University，2004.

［5］QI L.Eigenvalues of a real supersymmetric tensor［J］.J of Symbolic Computation，2005，40：1302-1324.

［6］QI L.Rank and eigenvalues of a supersymmetric tensor，the multivariate homogeneous polynomial and the algebraic hypersurface it defines［J］.J of Symbolic Computation，2006，41：1309-1327.

［7］QI L.Eigenvalues and invariants of tensors［J］.J of Math Analy Appl，2007，325：1363-1377.

［8］QI L，YU G，WU E X.Higher order positive semi-definite diffusion tensor imaging［J］.SIAM J on Imag Sci，2010，3：416-433.

［9］QI L.Symmetric nonnegative tensors and copositive tensors［J］.Linear Algebr Appl，2013，439：228-238.

［10］QI L，SONG Y.An even order symmetric B tensor is positive definite［J］.Linear Algebr Appl，2014，457：303-312.

［11］LIO Z，QI L，YE Y.Linear operators and positive semidefiniteness of symmetric tensor spaces［J］.Science China Mathematics，2015，58：197-212.

［12］DING W，QI L，WEI Y.Fast Hankel tensor-vector products and application to exponential data Fitting［J］.Numer Linear Algebr Appl，2015，22：814-832.

［13］LI G，QI L，XU Y.SOS Hankel tensors：Theory and application［J］.2014，ArXiv：1410.6989.

［14］QI L，XU C，XU Y.Nonnegative tensor factorization，completely positive tensors and an Hierarchically elimination algorithm［J］.SIAM J Matrix Anal Appl，2014，35：1227-1241.

［15］QI L.Hankel tensors：Associated Hankel matrices and Vandermonde decomposition［J］.Comm in Math Sci，2015，13：113-125.

［16］XU C.Hankel tensors，Vandermonde tensors，and their positivities［J］.Linear Algebra&Its Applications，2016，491：56-72.

［17］CHANG K C，PEARSON K，ZHANG T.Perron Frobenius theorem for nonnegative tensors［J］.Commu Math Sci，2008，6：507-520.

［18］LIM L H.Singular values and eigenvalues of tensors：A variational approach，in CAM-SAP2005［C］//1st IEEE Int'l Workshop on Comput.Palo Alto：Advances in Multi-Sensor Adaptive Processing，2005：129-132.

［19］GELFAND I，KAPRANOV M，ZELEVINSKY A.Discriminants，Resultants and Multidimensional Determinants，Birkhauser［M］.Boston：Publisher Birkhäuser，1994.

［20］XU C.The positivities of Vandermonde tensors［J］.Algebra，DOI：10.1080/03081087.2015.1122722.

责任编辑：谢金春

The CP decomposition of tensors，PSD tensors and Vandermonde tensors

XU Changqing1，QI Liqun2
（1.School of Mathematics and Physics，SUST，Suzhou 215009，China；2.Department of Applied Mathematics，The Hong Kong Polytechnic University，Hong Kong 999077，China）

Tensors，also called hypermatrices，are the generalization of matrices.In this paper，we first introduced some basic concepts related to tensors，such as eigenvalues and hyperdeterminant，and some basic operations on tensors （mainly the products of tensors）.Then，we reviewed the recent researches on the tensor rank-1 decomposition （also called the PARAFAC decomposition），positive semidefinite tensors，Hankel tensors and Vandermonde tensors.

tensor；tensor decomposition；Hankel tensor；Vandermonde tensor；positive semidefinite tensor

O151 MR（2000）Subject Classification：15A72

A

1672-0687（2016）02-0001-07

2015-12-30

国家自然科学基金重大项目（61190114/F0102）；香港政府研究基金资助项目（PolyU 502111；501212；501913；15302114）

徐常青（1966-），男，安徽安庆人，教授，博士，研究方向：张量分析与应用。祁力群（1946-），男，江苏扬州人，教授，博士，博士生导师，研究方向：计算数学与张量分析；俄罗斯Petrovskaya科学院外籍院士、美国密执根大学及中国科学院应用数学所客座教授、澳大利亚Curtin科技大学教授。