4错线性复杂度的2n周期序列计数

毕松松，戴小平

（安徽工业大学 计算机科学与技术学院，安徽 马鞍山243002）

4错线性复杂度的2n周期序列计数

毕松松，戴小平

（安徽工业大学 计算机科学与技术学院，安徽 马鞍山243002）

k错线性复杂度是衡量序列密码稳定性的重要指标之一。给出求满足4错线性复杂度的2n周期序列计数的过程。把4错线性复杂度的研究分解为对关键错误线性复杂度的研究，再用方体理论和筛选法讨论关键错误线性复杂度，得到相应关键错误点（下降点）4错线性复杂度的取值形式，及此时二元序列精确计数公式。最后，归纳出4错线性复杂度所有的取值形式和计算出满足4错线性复杂度的序列计数。

关键错误线性复杂度；k错线性复杂度；方体理论；筛选法

流密码是现代密码学的一个重要分支，研究具有高强度的流密码序列一直是密码学的重要工作之一。高强度的密码序列s要求序列具有高的线性复杂度L（s）和稳定的k错线性复杂度Lk（s）。k错线性复杂度是指当改变序列一个周期中至多k比特后，得到的所有序列中最小的线性复杂度。

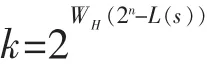
已知L（s）或Lk（s），求满足s的计数。文献［4］给出2n周期序列3错线性复杂度的完整序列计数公式。Meidl［5］给出2n周期二元序列1错线性复杂度和2错线性复杂度的分布情况。

给出求满足4错线性复杂度的2n周期序列计数的过程。其研究方法不同于文献［2，4-5］。通过把4错线性复杂度的研究分解为对关键错误线性复杂度的研究，再使用方体理论和筛选法讨论关键错误线性复杂度，最后得到满足4错线性复杂度的序列计数。

1 预备知识

设在有限域GF（2）域上有两序列x=（x1，x2，…，xn）和y=（y1，y2，…，yn），定义x+y=（x1+y1，x2+y2，…，xn+yn），其中“+”为异或运算或模2加法运算。

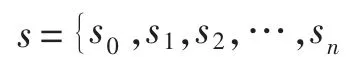
引理1［7］序列s是以N=2n为周期的二元序列，若L（s）=N，当且仅当WH（sN）为奇数。

引理2［7］序列s是以N=2n为周期的二元序列，若L（s）=0，则满足条件的s的个数为1；若L（s）=L，1≤L≤N则满足条件的s的个数为2L-1。

引理3［8］序列s1，s2是以N=2n为周期的两二元序列，如果L（s1）≠L（s2），则L（s1+s2）=max（L（s1），L（s2））；否则，L（s1+s2）＜L（s1）。

下面给出方体理论的基本内容，可参考文献［6，9-10］。

定义2 序列s是以N=2n为周期的二元序列，设L（s）=2n-（2i1+2i2+…+2im），0≤i1＜i2＜…＜im＜n，若m=1，s有 2个非零元素且形成一条边，边长为2i1，构成一个1方体；若m=2，s有4个非零元素且形成一个矩形，边长为2i1、2i2，构成一个2方体。一般而言，s中有2m-1个非零元素构成一个（m-1）方体，s中另外2m-1个非零元素也构成一个（m-1）方体，这2m-1对元素之间的距离均为2im，则这两个（m-1）方体构成一个m方体，2im为这两个（m-1）方体的距离。

引理4 序列s是以N=2n为周期的二元序列，L（s）=2n-（2i1+2i2+…+2im），0≤i1＜i2＜…＜im＜n，线性复杂度第一下降点K=2m。

引理5 序列s是以N=2n为周期的二元序列，若s的非零元素组成一个m方体，且其边长为2i1，2i2，…，2im，0≤i1＜i2＜…＜im＜n，则L（s）=2n-（2i1+2i2+…+2im）。

图1所示是一个边长为1，2，4的3方体，其线性复杂度为2n-（1+2+4）。这个3方体可由两个边长为1和4的2方体构成，且这两个2方体之间的距离为2。

下面为筛选法的基本内容，可参考文献［10］。

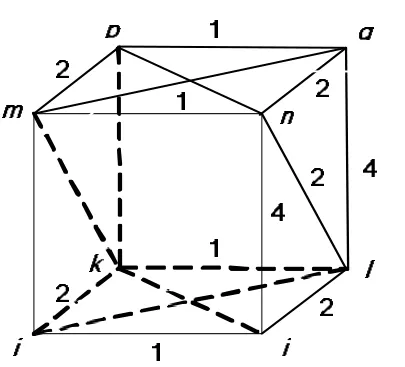
图1 引理5示意图

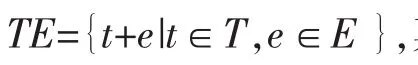
从TE中筛选出序列t+e，Lk（t+e）=c，需要排除的序列有两类，第一类是t+e∈TE，但Lk（t+e）＜c。第二类是x+u，y+v∈TE，并且Lk（x+u）=Lk（y+v）=c，x≠y，u≠v，WH（u）=WH（v）=k，但x+u=y+v。

对Lk（t+e）＜c的情况，设有序列v，WH（v）=k，使得Lk（t+u）=L（t+u+v）＜c。从而，有L（u+v）=c。问题可以转化成检查是否存在v，使得L（u+v）=c。对第二类的情况，因L（u+v）=c，根据异或运算规则，有x+y=u+v。而L（x）=L（y）=c，从而L（x+y）＜c，进而L（u+v）＜c。问题可以转化为检查是否存在v，使得L（u+v）＜c。

2 4错线性复杂度的二元序列计数

定义Nk（L）表示周期为2n二元序列s的个数，其中Lk（s）=L，0≤k≤2n。

定义Ni，k（L）表示周期为2n二元序列s的个数，其中Lk（s）=L，i（0≤i≤k）是序列s线性复杂度的第一下降点。

周期为N=2n的二元序列s，据引理1，若WH（sN）为奇数，则改变s一个周期的2个或4个元素，改变后序列的线性复杂度仍为2n；若WH（sN）为偶数，改变s一个周期的2个或4个元素后，线性复杂度可能下降。

定义Ni，k（c0，c1，L）表示周期为2n二元序列s的个数，其中s的线性复杂度为c0，2错线性复杂度为c1，4错线性复杂度为L，i（0≤i≤k）是序列s复杂度的第一下降点。

那么，满足L4（s）=L的序列s的个数为：N4（L）=N0，4（L）+N2，4（L）+N4，4（L）。若求N4（L），需分别求N0，4（L），N2，4（L）和N4，4（L）。

2.1 线性复杂度第一下降点k=0的序列计数

定理1 设s（n）是以N=2n为周期的二元序列，若L（s（n））=L2（s（n））=L4（s（n）），那么L4（s（n））=2n-（2i1+2i2+…+2im），0≤i1＜i2＜…＜im＜n，m≥3。

证明 s（n）是周期为2n的二元序列，其线性复杂度为L（s（n））=2n-（2i1+2i2+…+2im），0≤i1＜i2＜…＜im＜n，由引理4，使得Lk（s（n））＜L（s（n））的kmin=2m。 若L（s（n））=L2（s（n））=L4（s（n）），那么2m＞4。 从而，L4（s（n））=2n-（2i1+2i2+…+2im），0≤i1＜i2＜…＜im＜n，m≥3。

定理2 设s（n）是以2n为周期的二元序列，若L（s（n））=L2（s（n））=L4（s（n）），其中L4（s（n））=2n-（2i1+2i2+…+2im），0≤i1＜i2＜…＜im＜n，m≥3。那么满足条件的二元序列s（n）的个数为2L-1。

证明 由引理2可知，L（s（n））=L，若1≤L≤2n，周期为2n的二元序列s（n）的个数为2L-1。

2.2 线性复杂度第一下降点k=2的序列计数

线性复杂度第一下降点k=2，包含2种情况：（1）线性复杂度第一下降点k=2，第二下降点k＞4；（2）线性复杂度第一下降点k=2，且第二下降点k=4。

2.2.1 线性复杂度第一下降点k=2，第二下降点k＞4的序列计数

定理3 设 s（n）是以 2n为周期的二元序列，若 L（s（n））＞L2（s（n））=L4（s（n）），那么，L（s（n））=2n-2i，L2（s（n））= L4（s（n））=2n-（2i1+2i2+…+2im），0≤i1＜i2＜…＜im，m≥3。

证明 s（n）是周期为2n的二元序列，L（s（n））=2n-（2i1+2i2+…+2im），0≤i1＜i2＜…＜im，若L（s（n））＞L2（s（n）），即2错是线性复杂度第一下降点，那么L（s（n））=2n-2i；而第二下降点k＞4，那么L2（s（n））=L4（s（n））=2n-（2i1+2i2+…+2im），0≤i1＜i2＜…＜im，m≥3。

由定理3容易看出，研究线性复杂度第一下降点k=2，第二下降点k＞4的二元序列，可以通过研究线性复杂度第一下降点k=2的二元序列得到，但是要排除形如 L2（s（n））=2n-2i和L2（s（n））=2n-（2i+2j）两种情况。

定理 4 设 s（n）是以 2n为周期的二元序列，若 L（s（n））＞L2（s（n））=L4（s（n）），其中，L（s（n））=2n-2i，L2（s（n））= L4（s（n））=2n-（2i1+2i2+…+2im），0≤i1＜i2＜…＜im，m≥3。

（1）满足条件的二元序列s（n）的个数为22n-i-2×2L-1/（θ×2ε×2n-im-1）。

如果存在i0（0≤i0＜i），使得2n-（2i0+2i）＜L，那么θ=2i-i0；否则，θ=1。当i＜im时，若2n-（2i+2im）＞L，ε=0；若2n-（2i+2im）＜L＜2n-2im，ε=1。

（2）如果L2（s（n））=0，以周期为2n的二元序列s（n）的个数为22n-i-2。

证明 设TE=｛t+e|t∈T，e∈E｝，T=｛t|L（t）=L｝，其中L（t）=2n-（2i1+2i2+…+2im），并且L（e）=2n-2i。使用筛选法，从TE中筛选出L2（t+e）=L的序列t+e。

（1）由引理2可知，L（t）=L，若1≤L≤2n，周期为2n的二元序列的t个数为2L-1；否则，t的个数为1。

（2）下面求出e的个数，WH（e）=2，L（e）=2n-2i。

设s（i）是以2i为周期的二元序列，若L（s（i））=2i且WH（s（i））=1，那么序列s（i）的个数是2i。周期翻倍，变成2i+1，若线性复杂度为2i+1-2i=2i且WH（s（i+1））=2，那么s（i+1）的个数还是2i。

所以，满足条件WH（e）=2，L（e）=2n-2i的二元序列e的个数为2i×（22）n-i-1=22n-i-2。

（3）由上述可知：当L（t）=0时，t+e的个数为22n-i-2，（2）得证；当L（t）＞0时，t+e的个数小于22n-i-2×2L-1，因为此时t+e的个数中存在重复的情况，即存在s+u，t+v∈TE，L2（s+u）=L2（t+v）=L，其中s≠t，u≠v，但s+u=t+v。排除重复序列的思想源自筛选法第二类的情况，需要检查是否存在这样的v，使得L（u+v）=L（s+t）＜L，以及这时v的个数。其中WH（u）=WH（v）=2，L（u）=L（v）=2n-2i。下面考虑两种情况。

①跟i0，i有关

对于∀u∈E，若2n-（2i0+2i）＜L，0≤i0＜i，存在2i-i0-1个v，θ=2i-i0，使得L（u+v）＜L。

下面进行举例说明。

假设n=4，i=3时，存在序列u（4）=｛1000 0000 1000 0000｝；

满足2n-（22+23）=4＜L的v的个数为1，v=｛0000 1000 0000 1000｝；

满足2n-（21+23）=6＜L的v的个数为3，v=｛0000 0010 0000 0010｝；v=｛0010 0000 0010 0000｝；

满足2n-（20+23）=7＜L的v的个数为7，v=｛0000 0001 0000 0001｝；v=｛0000 0100 0000 0100｝；v=｛0001 0000 0001 0000｝；v=｛0100 0000 0100 0000｝。

②跟im＜ω＜n有关

对于im＜ω＜n，存在3×（22）ω-im-1个序列v，使得L（u+v）=2n-（2i+2ω）＜L或L（u+v）=2n-2ω＜L。

对于满足任意条件的v有2个非零元素，若将v的周期加倍，那么一个原序列将会产生22个新序列。将周期变成2n，存在3+3×22+…+3×（22）n-im-2=（22）n-im-1-1个v，使得L（u+v）＜L。

下面给出例子说明。

假设 n=4，i=0时，设有序列 u（4）=｛1100 0000 0000 0000｝，只存在 v=｛0000 0000 1100 0000｝，使L（u（4）+v）=2n-（2i+2ω）=24-（20+23）=7。只存在v=｛0100 0000 1000 0000｝，v=｛1000 0000 0100 0000｝，使得L（u（4）+v）=L（u（4）+v）=2n-2ω=24-23=8。

由上可知，当im＜ω＜n时，在2n-（2i+2im）＜L＜2n-2im时，v的个数增加（22）n-im-1，ε=1。

综上所述，满足L（s（n））=2n-2i＞L2（s（n））=L4（s（n））且L4（s（n））=L的2n周期二元序列s（n）的计数公式为

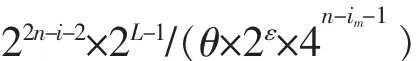
当i=im或2n-（2i+2im）＞L时，ε=0；当2n-（2i+2im）＜L＜2n-2im时，ε=1。

如果存在i0，使得2n-（2i0+2i）＜L，0≤i0＜i，那么θ=2i-i0；否则，θ=1。

定理 4已经求得在已知 L（s（n））=c0，L（s（n））＞L2（s（n））=L4（s（n））=L时二元序列 s（n）的计数公式。 当已知L4（s（n））=L，而未知L（s（n））=c0时，可以根据定理3给出的L与c0的约束关系，从L推测出c0，进而得到序列s（n）的计数。

例1 若n=4，L（s（n））＞L2（s（n））=L4（s（n））=9，求满足条件的以24为周期的二元序列s（n）的个数。由定理3知，L4（s（n））的线性复杂度可以由一个m≥3方体表示，L（s（n））的线性复杂度只能由一个1方体表示。因为n=4，L4（s（n））=9，可以计算出L（s（n））的值为12，14或15。所以，当L（s（n））＞L2（s（n））=L4（s（n））时，N2，4（9）=N2，4（12，9，9）+N2，4（14，9，9）+N2，4（15，9，9）=1 024+2 048+4 096=7 168。

2.2.2 线性复杂度第一下降点k=2，第二下降点k=4的序列计数

线性复杂度第一下降点k=2，第二下降点k=4的二元序列分布，文献［10］已给出了相关的结论和证明。

引理6 设s（n）是以2n为周期的二元序列，若L（s（n））＞L2（s（n））＞L4（s（n）），那么，L（s（n））=2n-2i0，或者L2（s（n））= 2n-（2i+2j），i0＜i或者i＜i0＜j，但是L2（s（n））≠2n-（20+21）。

引理7 设s（n）是以2n为周期的二元序列，若L（s（n））＞L2（s（n））＞L4（s（n）），并且L（s（n））=2n-2i0，L2（s（n））=2n-（2i+2j），i0＜i或者i＜i0＜j，L2（s（n））≠2n-（20+21），那么

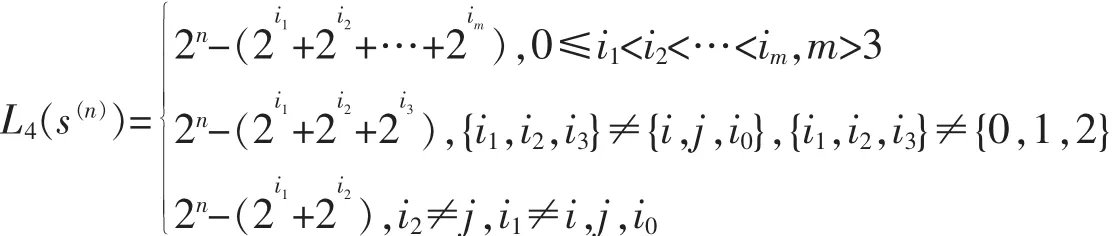
引理8 设s（n）是以2n为周期的二元序列，若L（s（n））＞L2（s（n））＞L4（s（n）），并且L（s（n））=2n-2i0，L2（s（n））=2n-（2i+2j），i0＜i或者i＜i0＜j，L2（s（n））≠2n-（20+21），并且

那么，满足条件的二元序列s（n）的个数为（24n-j-i-i0-4）×2L-1/（2δ×2ε×16n-im-1）。

如果i0＞i，γ=2；或则γ=1。若2n-（2i+2i0+2j）＞L，δ=0；若2n-（2i+2i0+2j）＜L＜2n-（2i0+2j），δ=1；若2n-（2i0+2j）＜L，δ=2。当j=im或2n-（2j+2im）＞L，ε=0；当2n-（2j+2im）＜L＜2n-（2i+2im），ε=1；当2n-（2i+2im）＜L＜2n-（2i0+2im），ε=2；当2n-（2i0+2im）＜L＜2n-2im，ε=3。

由以上知，L（s（n））＞L2（s（n））＞L4（s（n））时，若只给出L4（s（n））=L，可以通过相关约束关系求出L（s（n））和L2（s（n）），进而得到二元序列s（n）的计数。

例2 若n=4，L（s（n））＞L2（s（n）），L4（s（n））=5，求满足条件的以24为周期的二元序列s（n）的个数。

如果L（s（n））＞L2（s（n））＞L4（s（n）），由引理8得到L（s（n））=15，L2（s（n））=10；L（s（n））=14，L2（s（n））=11；L（s（n））=12，L2（s（n））=7或L（s（n））=12，L2（s（n））=6。

如果L（s（n））＞L2（s（n））=L4（s（n）），由定理3得到L（s（n））=15；L（s（n））=14；L（s（n））=12；L（s（n））=8。

所以，当n=4，L4（s（n））=5，而2错为线性复杂度第一下降点时，

N2，4（5）=N2，4（8，5，5）+N2，4（12，5，5）+N2，4（14，5，5）+N2，4（15，5，5）+N2，4（12，6，5）+N2，4（12，7，5）+N2，4（14，11，5）+N2，4（15，10，5）=64+128+512+1 024+128+256+2 048+4 096=8 256

2.3 线性复杂度第一下降点k=4的序列计数

定理5 设s（n）是以2n为周期的二元序列，若L（s（n））=L2（s（n））＞L4（s（n）），那么L（s（n））=L2（s（n））=2n-（2i+2j）。

证明 s（n）是周期为2n的二元序列，L（s（n））=2n-（2i1+2i2+…+2im），0≤i1＜i2＜…＜im，若4错是线性复杂度第一下降点，那么L（s（n））=L2（s（n））=2n-（2i+2j）。

定理6 设s（n）是以2n为周期的二元序列，若L（s（n））=L2（s（n））＞L4（s（n））且有L（s（n））=L2（s（n））=2n-（2i+2j），那么

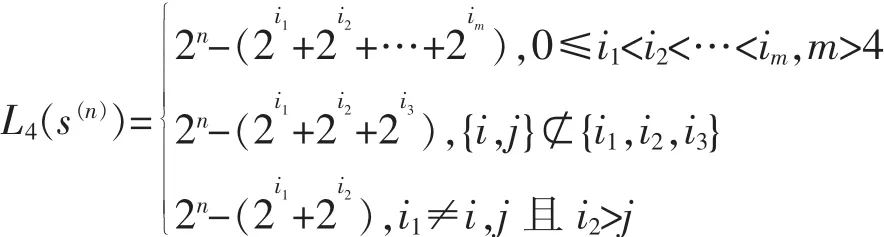
证明 源自筛选法中的第一类的情况，并构造如下框架：设TE=｛t+e|t∈T，e∈E｝，其中T=｛t|L（t）=L｝，E= ｛e|WH（e）=4｝，使用筛选法，从TE中筛选出满足L4（t+e）=L的序列t+e。现研究t+u∈TE，但L4（t+u）＜L=L4（s（n））的情况。这种情况等价于检查是否存在v，v∈E，使得L（u+v）=L。对于∀u∈E，有L4（u）=L4（s（n））。

当L4（s（n））=2n-（2i1+2i2+2i3）＜2n-（2i+2j）时，使用反证法证明｛i1，i2，i3｝不包含｛i，j｝。设n=4，i=0，j=2时，有u（4）=｛1100 1100 0000 0000｝。存在v=｛0000 0000 1100 1100｝，使得L（u+v）=25-（20+22+23），所以有L4（t+u）＜25-（20+22+23），因此，｛i1，i2｝≠｛i，j｝。

同理可得｛i2，i3｝≠｛i，j｝。进而，｛i1，i2，i3｝不包含｛i，j｝。

同理有i1≠i，j且i2＞j。

定理7 设s（n）是以2n为周期的二元序列，若L（s（n））=L2（s（n））＞L4（s（n））且有L（s（n））=L2（s（n））=2n-（2i+2j），其中

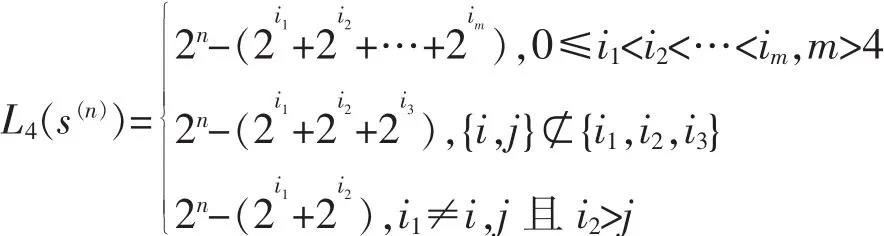
（1）满足条件的二元序列s（n）的个数为24n-2j-i-6×2L-1/（θ1×θ2×θ3×2ε×16n-im-1）。

如果存在k0，使得2n-（2i+2k0+2j）＜L，i＜k0＜j，那么θ1=2j-k0；否则，θ1=1。

如果存在k1，使得2n-（2k1+2j）＜L，i＜k1＜j，那么θ2=2j-k1；否则，θ2=1。

如果存在k2，使得2n-（2k2+2i+2j）＜L，0≤k2＜i，那么θ3=2i-k2；否则，θ3=1。

当j＜im时，若2n-（2i+2j+2im）＜L，ε=0；若2n-（2i+2j+2im）＜L＜2n-（2j+2im），ε=1；若2n-（2j+2im）＜L＜2n-（2i+2im），ε=2；若2n-（2i+2im）＜L＜2n-2im，ε=3。

（2）如果L4（s（n））=0，以周期为2n的二元序列s（n）的个数为24n-2j-i-6。

证明 设TE=｛t+e|t∈T，e∈E｝，T=｛t|L（t）=L｝，E=｛e|WH（e）=4｝，其中L（t）=2n-（2i1+2i2+…+2im），并且L（e）= L2（e）=2n-（2i+2j）。使用筛选法，从TE中筛选出L4（t+e）=L的序列t+e。

1）由引理2可知，L（t）=L，若1≤L≤2n，周期为2n的二元序列的t个数为2L-1；否则，t的个数为1。

2）下面求出e的个数，WH（e）=4，L（e）=L2（e）=2n-（2i+2j）。

设s（i）是以2i为周期的二元序列，若L（s（i））=2i且WH（s（i））=1，那么序列s（i）的个数是2i。周期翻倍，变成2i+1，若改变后序列线性复杂度为2i+1-2i=2i且WH（s（i+1））=2，那么s（i+1）的个数为2i。周期变为2j，（j＞i），序列s（j）的个数为（22）j-i-1×2i=22j-i-2。周期翻倍，变成2j+1，若改变后序列线性复杂度为2j+1-（2j+2i）且WH（s（j+1））=4的个数也是22j-i-2。

所以，满足条件WH（e）=4，L（e）=L2（e）=2n-（2i+2j）的二元序列e的个数为22j-i-2×（24）n-j-1=24n-2j-i-6。

3）由上述可知，当L（t）=0时，t+e的个数为24n-2j-i-6，（2）得证；当L（t）＞0时，t+e的个数小于24n-2j-i-6×2L-1，因为此时t+e的个数中存在重复的情况，即存在s+u，t+v∈TE，L4（s+u）=L4（t+v）=L，其中s≠t，u≠v，但s+u=t+v。排除重复序列的思想源自筛选法第二类的情况，需要检查是否存在这样的v，使得L（u+v）=L（s+t）＜L，以及这时v的个数。其中WH（u）=WH（v）=4，L（u）=L（v）=2n-（2i+2j）。下面考虑两种情况。

①跟i，j，i0有关

定理6已得，L4（s（n））不存在形如，2n-2im，2n-（2j+2im），2n-（2i+2im）和部分2n-（2i1+2i2+2i3）的形式。这些值使得L4（s（n））取值不连续。

对于∀u∈E，若2n-（2i+2k0+2j）＜L，i＜k0＜j，存在2j-k0-1个v，θ1=2j-k0；若2n-（2k1+2j）＜L，i＜k1＜j，存在2j-k1-1 个v，θ2=2j-k1；若2n-（2k2+2i+2j）＜L，0≤k2＜i，存在2i-k2-1个v，θ3=2i-k2。

若L同时满足上述三种情况或其中两种情况时，v的个数为θ1×θ2×θ3-1。

下面给出例子说明。

假设n=4，i=0，j=3时，设有序列u（5）=｛1100 0000 1100 0000｝，那么 满足2n-（2i+2k0+2j）=3＜L，i＜k0＜j，k0=2 的v的总个数有1个，v=｛0000 1100 0000 1100｝；满足2n-（2k+2j）=4＜L，k=2的v的总个数有3个。其中满足2n-（2i+2k0+2j）=3＜L，k0=2的v个数2个；满足2n-（2k1+2j）=4＜L，k1=2的v个数2个。所以v的个数共为2×2-1=3。

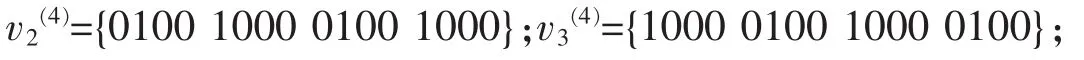
满足2n-（2i+2k+2j）=5＜L，k=2的v的总个数有7个。其中满足2n-（2k1+2j）=4＜L，k1=2的v个数2个；满足2n-（2i+2k0+2j）=3＜L，k0=2的v个数4个。所以v的个数共为2×4-1=7。

②跟im＜ω＜n有关

对于 im＜ω＜n，存在15×（24）ω-im-1个序列 v，使得L（u+v）=2n-（2i+2j+2ω）＜L或 L（u+v）=2n-（2j+2ω）＜L或L（u+v）=2n-（2i+2ω）＜L或L（u+v）=2n-2ω＜L。

对于满足任意条件的v有4个非零元素，若将v的周期加倍，那么一个原序列将会产生24个新序列。当周期变为2n时，存在15+15×24+…+15×（24）n-im-2=（24）n-im-1-1个v，使得L（u+v）＜L。

下面用例子说明上面的结论。

假设n=4，i=0，j=1，设有序列u（4）=｛1111 0000 0000 0000｝。那么只存在v=｛0000 0000 1111 0000｝，使得L（u（4）+v）=2n-（2i+2j+2ω）=24-（20+21+23）=5。只存在v=｛0101 0000 1010 0000｝，v=｛1010 0000 0101 0000｝，使得L（u（4）+v）=L（u（4）+v）=2n-（2j+2ω）=24-（21+23）=6。只存在 v=｛0011 0000 1100 0000｝，v= ｛0110 0000 1001 0000｝，v=｛1001 0000 0110 0000｝，v=｛1100 0000 0011 0000｝，使得L（u（4）+v）=…= L（u（4）+v）=2n-（2i+2ω）=24-（20+23）=7。只存在v=｛0001 0000 1110 0000｝，…，v=｛1110 0000 0001 0000｝，使得L（u（4）+v）=…=L（u（4）+v）=2n-2ω=24-23=8。

由以上可知，当j＜im＜n时

若2n-（2i+2j+2im）＞L，ε=0；若2n-（2i+2j+2im）＜L＜2n-（2j+2im），v的个数增加（24）n-im-1，ε=1；若2n-（2j+2im）＜L＜2n-（2i+2im），v的个数增加3×（24）n-im-1，ε=2；若2n-（2i+2im）＜L＜2n-2im，v的个数增加7×（24）n-im-1，ε=3。

综上所述，满足L（s（n））=L2（s（n））=2n-（2i+2j）＞L4（s（n））且L4（s（n））=L的2n周期二元序列s（n）的计数公式为

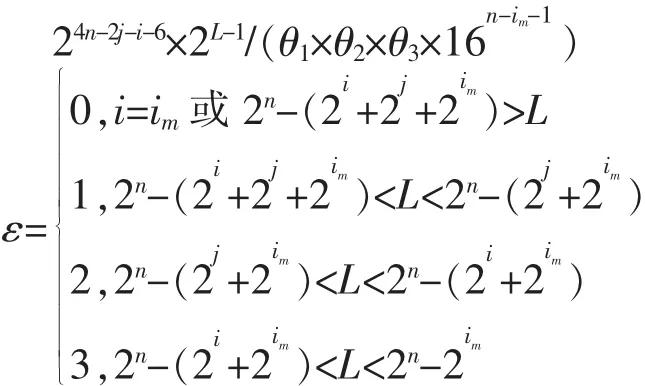
如果存在k0，使得2n-（2i+2k0+2j）＜L，i＜k0＜j，那么θ1=2j-k0；否则，θ1=1。

如果存在k1，使得2n-（2k1+2j）＜L，i＜k1＜j，那么θ2=2j-k1；否则，θ2=1。

如果存在k2，使得2n-（2k2+2i+2j）＜L，0≤k2＜i，那么θ3=2i-k2；否则，θ3=1。

由以上知，若L（s（n））=L2（s（n））＞L4（s（n）），当已知L4（s（n））=L，而未知L（s（n））和L2（s（n））时，可以通过约束关系求得L（s（n））和L2（s（n）），进而，求出二元序列s（n）的计数。

例2 若n=4，L（s（n））=L2（s（n））＞L4（s（n））=3，求满足条件的二元序列s（n）的个数。由定理5知，L（s（n））的线性复杂度只能由一个2方体表示，并且｛i1，i2，i3｝不包括｛i，j｝。可以计算出L（s（n））的值为6，10或13。所以，当L （s（n））=L2（s（n））＞L4（s（n））时，N4，4（3）=N4，4（6，6，3）+N4，4（10，10，3）+N4，4（13，13，3）=16+64+1 024=1 104。

2.4 4错线性复杂度的序列计数

由2.1，2.2，2.3小节可以得到

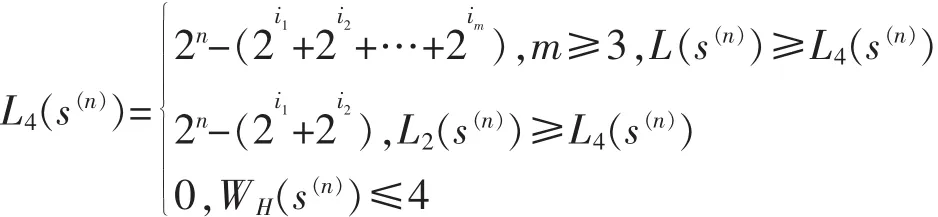
并且给出了计算N0，4（L），N2，4（L）和N4，4（L）的过程。那么，满足L4（s（n））=L的序列s（n）的个数为

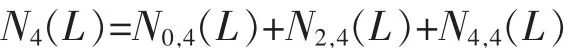
求解N4（L）过程，为算法1所示，例3为详述过程：

算法1：求满足4错线性复杂度二元序列计数

Input：4错线性复杂度L4（s），序列周期N

Output：二元序列计数N4

例3 若n=5，L4（s（n））=18，求满足条件的以25为周期的二元序列s（n）的个数。

若L（s（n））=L2（s（n））=L4（s（n）），由定理1可得L（s（n））=18。进而，N0，4（18）=N0，4（18，18，18）=131 072。

若L（s（n））＞L2（s（n））=L4（s（n）），由定理4可知L（s（n））的值可为24，28，30或31。

若L（s（n））＞L2（s（n））＞L4（s（n）），由引理8可知L（s（n）），L2（s（n））的值可为31，26；31，22；31，20；30，27；30，23或28，23。 进而，N2，4（18）=N2，4（24，18，18）+N2，4（28，18，18）+N2，4（30，18，18）+N2，4（31，18，18）+N2，4（31，26，18）+N2，4（31，22，18）+N2，4（31，20，18）+N2，4（30，27，18）+N2，4（30，23，18）+N2，4（28，23，18）=191 889 408。

当L（s（n））=L2（s（n））＞L4（s（n））时，由定理7可得L（s（n））的值为29，27，23。进而，N4，4（18）=N4，4（29，29，18）+N4，4（27，27，18）+N4，4（23，23，18）=44 040 192。

所以，N4（18）=N0，4（18）+N2，4（18）+N4，4（18）=236 060 672。

3 结语

文中给出求满足4错线性复杂度的2n周期序列计数的过程。通过将4错线性复杂度的研究分解为对关键错误线性复杂度的研究，再使用方体理论和筛选法讨论关键错误线性复杂度，最后得到满足4错线性复杂度序列的计数，并且用计算机编程得到的数据佐证了给出的求解过程的正确性。文中的研究方法可以推广到求解其他k错线性复杂度序列计数。但是，随着k值的增大，其求解过程将变得繁琐。下一步，将研究简便的方法来讨论序列k错线性复杂度，力争进一步完善k错线性复杂度的研究。

［1］KUROSAWA K，SATO F，SAKATA T，et al.A relationship between linear complexity and k-error linear complexity［J］.IEEE Transactions on Information Theory，2000，46（2）：694-698.

［2］皮飞，戚文峰.二元周期序列的4错线性复杂度［J］.电子学报，2011，39（12）：2914-2920.

［3］ETZION T，KOLOKOTRONIS N，LIMNIOTIS K，et al.Properties of the error linear complexity spectrum［J］.IEEE Trans on Inform Theory，2009，55 （10）：4681-4686.

［4］周建钦.具有2n线性复杂度的2n周期二元序列的3错线性复杂度［J］.应用数学学报，2013，36（3）：399-413.

［5］MEDIDL W.On the stability of 2n-periodic binary sequence［J］.IEEE Trans on Information Theory，2005，51（3）：1151-1155.

［6］ZHOU Jianqin.On the k-error linear complexity for 2n-periodic binary sequences via Cube Theory［J］.Eprint Arxiv，2013，73（1）：55-75.

［7］周建钦，戴小平.具有稳定k错线性复杂度的周期序列［J］.通信学报，2011，32（11A）：213-220.

［8］戴小平，毕松松，王喜凤，等.k错线性复杂度具有第二下降点的 2n周期序列［EB/OL］.［2015-04-10］.http：//www.cnki.net/kcms/detail/ 31.1289.TP.20150410.1634.004.html.

［9］ZHOU J Q，LIU W Q.The k-error linear complexity distribution for 2n-periodic binary sequence［J］.Designs Codes and Cryptography，2014，73：55-75.

［10］ZHOU J Q，LIU W Q，WANG X F.Structure Analysis on the k-error Linear Complexity of 2n-periodic Binary Sequences［EB/OL］.［2014-08-09］.http：//arxiv.org/abs/1312.6927.

责任编辑：艾淑艳

Counting functions for 2n-periodic binary sequences with 4-error linear complexity

BI Songsong，DAI Xiaoping
（School of Computer Science&Technology，Anhui University of Technology，Ma'anshan 243002，China）

The k-error linear complexity is one of the important measures for assessing the stability of sequence cipher.First，we presented the process of counting functions of 2n-periodic binary sequences with given 4-error linear complexity.Then we studied the critical error linear complexity via cube theory and sieve method.The possible values of the 4-error linear complexity of corresponding critical error point（descent point）were obtained and the number of sequences with given 4-error linear complexity of corresponding critical error point were established.Finally，we got the all the possible value forms of the 4-error linear complexity and the counting functions of 2n-periodic binary sequences.

critical error linear complexity；k-error linear complexity；cube theory；sieve method

TP918.1

A

1672-0687（2016）02-0055-09

2015-04-16

安徽省自然科学基金资助项目（1208085MF106）；安徽省教育厅自然科学基金资助项目（KY2013Z025）；安徽工业大学校青年科学基金资助项目（QZ201412）

毕松松（1990-），男，安徽凤台人，硕士研究生，研究方向：信息安全与密码学。