奥氏体不锈钢S30408抗拉强度分布规律研究

刘 岑，吴元祥，刘 兵，袁小会，陈 刚，刘小宁

（武汉软件工程职业学院机械工程学院，湖北武汉 430205）

奥氏体不锈钢S30408抗拉强度分布规律研究

刘 岑，吴元祥，刘 兵，袁小会，陈 刚，刘小宁

（武汉软件工程职业学院机械工程学院，湖北武汉 430205）

研究钢材抗拉强度分布规律是机械强度可靠性设计的基础。基于奥氏体不锈钢S30408在液氮温度（－196℃）时的抗拉强度的60组试验数据，通过数理统计方法对其有效性及抗拉强度的分布规律进行了研究，结果表明：1）在单侧置信度为99%时，60组试验数据中含有1组无效数据；2）在显著度为0.05时，抗拉强度是基本符合正态分布的随机变量；3）无效试验数据对钢材抗拉强度分布规律的影响不可忽视。

机械强度；奥氏体不锈钢；S30408；抗拉强度；有效性；分布规律

抗拉强度是钢材机械性能的主要参数之一，抗拉强度的分布规律是指考虑抗拉强度的随机不确定性时，抗拉强度分布区间与频数的关系，即抗拉强度分布的概率密度函数。研究钢材抗拉强度的分布规律，不但是建立机械强度可靠性设计方法的基础[111]，而且还可改进目前确定抗拉强度工程许用值的方法[12]。

试验数据是分析与探索钢材抗拉强度分布规律的依据，如何判别试验数据的有效性[1，13－15]，是分析与探索抗拉强度分布规律的基础工作。本文应用数理统计理论，建立了判别试验数据有效性的方法。根据钢材使用温度，抗拉强度分为常温、高温与低温3种状态，基于奥氏体不锈钢S30408在液氮温度（－196℃）时的试验数据[12]，研究了低温抗拉强度的分布规律。

1　理论分析

根据数理统计理论[13－15]，工程上采用有限的试验数据分析钢材抗拉强度的分布规律，如果通过试验测量得到n组试验数据Ri（i＝1，2，…，n），不难得到试验数据的准确度与精密度：式中：分别为n组试验数据的准确度与精密度；Ri为抗拉强度的第i个试验数据。

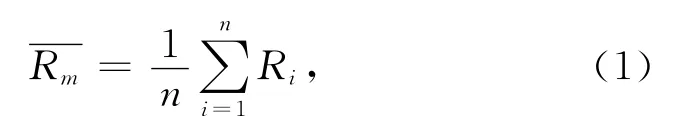
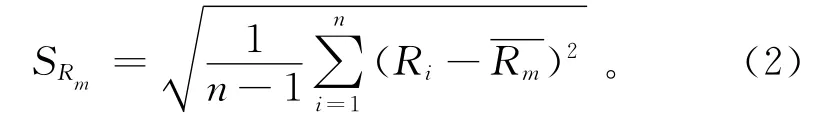
1.1试验数据有效性的判别方法

由于试验的影响因素比较多，因此，必须对试验数据的有效性进行判别，剔除因意外因素影响而形成的无效数据。

表1　t与系数Tab.1 Coefficient and t

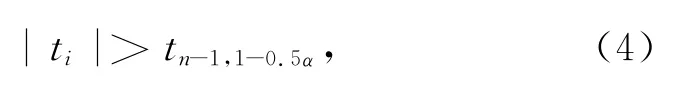
对于试验数据Ri，其判据为若表明试验数据Ri不是有效数据，需要剔除；若存在r个无效数据，则对（n－r）个有效数据需要重新计算其准确度与精密度。

工程上通常取α＝0.02，即在单侧置信度为99%时，分析试验数据的有效性。表明有99%的把握认为剔除的无效数据是意外因素影响而形成的。

1.2分布规律的假设检验

钢材抗拉强度是随机变量，在试验数据比较少时，工程上认为其概率密度函数符合正态分布[1]；随着人们认识的提高，以及试验数据的增加，对抗拉强度Rm分布规律进行假设检验成为可能，其具体方法如下[1，14－15]。

1）假设。假设抗拉强度Rm的概率密度函数符合正态分布，即假设Rm是符合正态分布的随机变量。

2）分组。根据有效数据个数（n－r），把有效试验数据R1，R2，…，Rn－r分为M个区间，M＝1＋3.3lg（n－r），并取整数。

4）计算理论频数。对于符合正态分布的随机变量R，统计量Ri落在分组区间[a1，a2]，[a2，a3]，…，[aM，aM＋1]内的理论概率为，j＝1，2，…，M，式中，Φ（·）为标准正态积分；a1＝（Ri）min，aM＋1＝（Ri）max，（Ri）min，（Ri）max分别为Ri中的最小值与最大值。

从2016年随州市的高职院校专业设置情况来看，在随州市的几大高职院校中第三产业有着最高的专业设置率，国际贸易实务专业这一专业的设置率最高，除此之外就是计算机、商务英语、物流管理等专业。数控技术是在随州市高职院校专业设置中服务第二产业专业中设置率最高的专业。值得注意的是在随州市高职院校内服务第三产业的专业数量达到了所有专业数量的一半左右，主要包含有应用日语、动漫设计与制作、旅游管理、投资与理财、电子商务等。

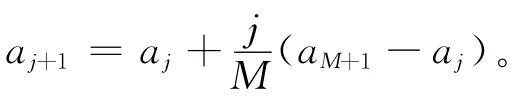
对于（n－r）个有效试验数据，其统计量Ri落在分组区间[aj，aj＋1]内的理论频数为（n－r）×pj。

5）计算每个分组区间实际频数（Nj）与理论频数（n－r）×pj差异的皮尔逊统计量之和，即计算

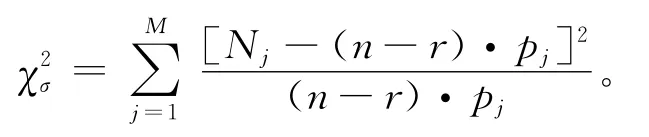
工程上一般取显著度δ＝0.05，本文所用的χ2系数见表1[1，14]。

2　分布规律的假设检验

2.1试验数据及其有效性判别

奥氏体不锈钢S30408是制造深冷容器的常用钢材，在液氮温度（－196℃）时，文献[12]获得了其低温抗拉强度Rm的60组试验数据，见表2。

表2　低温抗拉强度Rm的60组试验数据Tab.2 60sets test data of low temperature tensile strength Rm

将表2的试验数据代入式（1）与式（2），可得到低温抗拉强度Rm准确度与精密度的统计数据，如表3所示。

表3　试验数据统计Tab.3 Test data statistics

用式（3）与式（4）及表3数据，可知第1组试验数据Rm1＝1 490MPa的｜t1｜＝2.464＞t59，0.99＝ 2.388，因此，该数据是无效的需要剔除，其他59组试验数据的准确度与精密度列入表3，经用式（3）与式（4）判别，59组试验数据的＝ 2.393，都是有效数据。

2.2低温抗拉强度分布规律的假设检验

假设低温抗拉强度Rm的概率密度函数符合正态分布。对于59组有效试验数据，由于1＋3.3lg 59＝6.84，因此将其分别分为7个区间，其自由度为f＝7－1－2＝4，取显著度δ＝0.05，由表1可知，皮尔逊统计的临界值每个分组区间实际频数（Nj）与理论频数（n－r）×pj差异的皮尔逊统计量之和见表4。

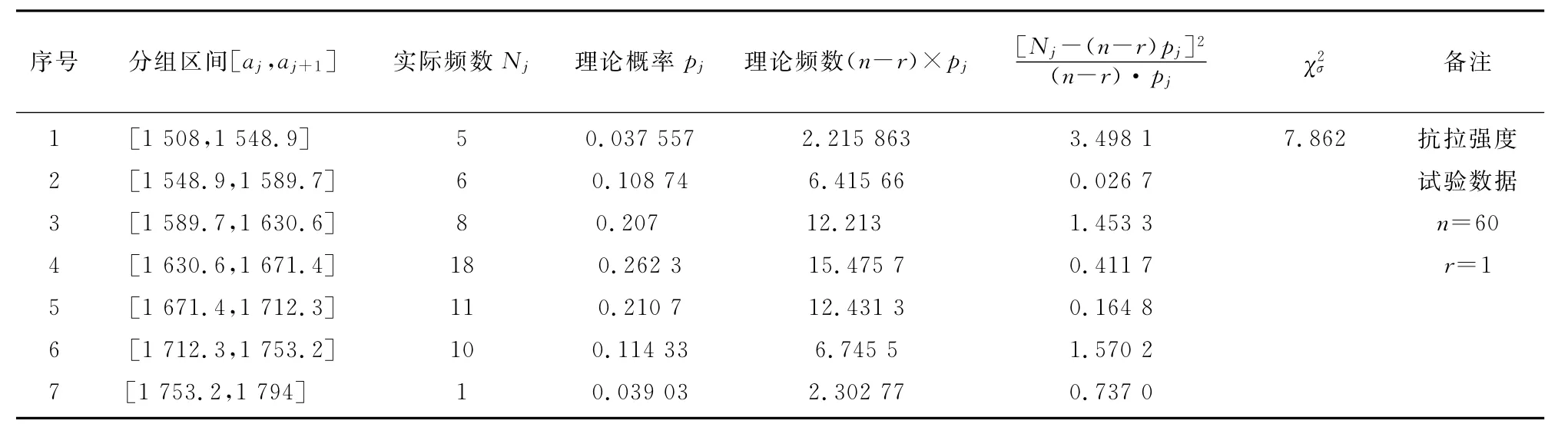
表4　低温抗拉强度Rm的皮尔逊统计量（59组有效试验数据）Tab.4 Statisticχ2of low temperature tensile strength Rm（59sets validity test data）

由表4可知：Rm的χ2σ＝7.862，小于临界值9.488，表明在显著度为0.05时，即有95%的把握认为低温抗拉强度Rm的概率密度函数符合正态分布。

3　讨 论

若不考虑数据的有效性，按上述方法计算60组低温抗拉强度试验数据的皮尔逊统计量之和，见表5。

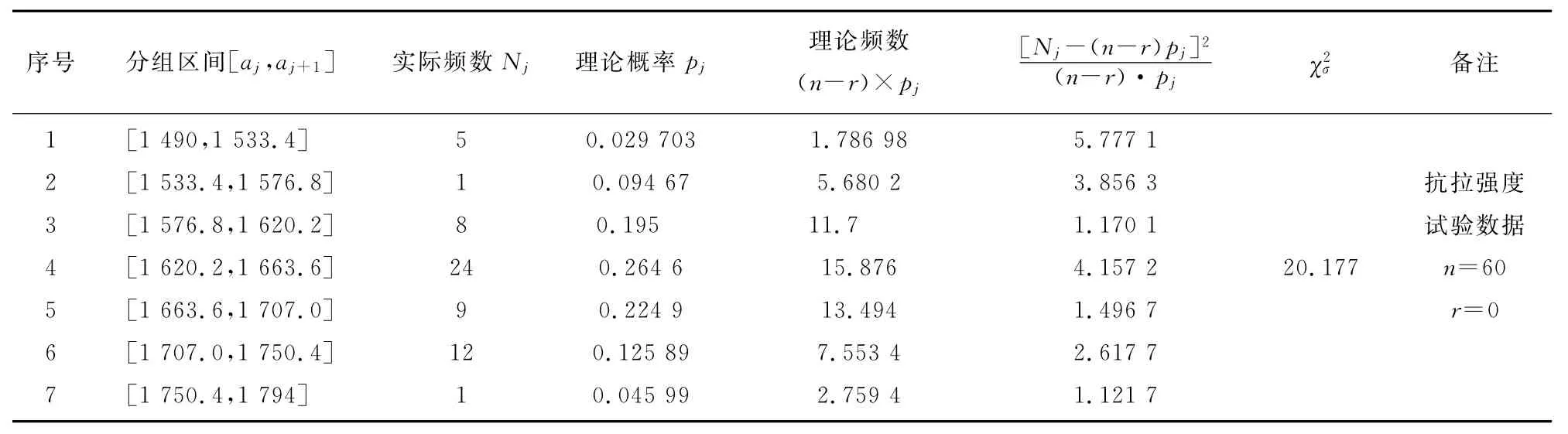
表5　低温抗拉强度Rm的皮尔逊统计量（60组试验数据）Tab.5 Statisticχ2of low temperature tensile strength Rm（60sets test data）

由表5知，显著度为0.05时，如果不剔除无效数据，Rm的χ2σ大于皮尔逊统计量的临界值9.488，不能接受Rm是符合正态分布随机变量的假设；根据2.2节的分析可知，这一结论并不正确。

比较表4与表5可知，试验数据的有效性对钢材抗拉强度分布规律的影响不可忽视，若不剔除无效数据，关于钢材抗拉强度分布规律的结论有可能不正确。

4　结 语

1）应用数理统计方法研究试验数据的有效性，是分析钢材机械性能参数分布规律的基础工作，准确剔除无效试验数据，是正确分析钢材机械性能参数分布规律的关键；文中建立了试验数据有效性的分析方法，在单侧置信度为99%时，研究了奥氏体不锈钢S30408低温抗拉强度试验数据的有效性。

2）显著度为0.05时，奥氏体不锈钢S30408在液氮温度（－196℃）时的抗拉强度，是基本符合正态分布的随机变量。

3）建立机械强度可靠性设计方法，必须构建钢材机械性能参数分布规律的数据库，还需同行共同努力。

／References：

[1] 徐灏.机械强度的可靠性设计[M].北京：机械工业出版社，1984.

[2] 袁小会，刘岑，吴元祥，等.单层厚壁圆筒容器爆破压力的分布规律与参数[J].武汉工程大学学报，2014，36（2）：49－55.YUAN Xiaohui，LIU Cen，WU Yuanxiang，et al.Distribution law and parameters of monolayer thick－wall cylindrical vessel burst pressure[J].Journal of Wuhan Institute of Technology，2014，36（2）：49－55.

[3] 刘小宁，张红卫，韩春鸣，等.耐压试验时薄壁内压容器静强度的可靠度[J].机械设计与研究，2013，29（1）：39－40.LIU Xiaoning，ZHANG Hongwei，HAN Chunming，et al.Reliability of thin－walled internal pressure vessels static strength in pressure test[J].Machine Design ＆Research，2013，29（1）：39－40.

[4] 李清，袁小会，刘岑，等.有效试验数据对钢材机械性能分布规律的影响[J].武汉工程大学学报，2015，37（4）：69－73.LI Qing，YUAN Xiaohui，LIU Cen，et al.Validity test data effect on steel mechanical properties distribution law[J].Journal of Wuhan Institute of Technology，2015，37（4）：69－73.

[5] 刘小宁，张红卫，刘岑，等.钢制薄壁内压容器静强度的可靠性设计[J].工业安全与环保，2011，37（3）：48－50.LIU Xiaoning，ZHANG Hongwei，LIU Cen，et al.Reliability design of static strength for steel thin wall ento－pressure vessel [J].Industrial Safety and Environ－mental Protection，2011，37（3）：48－50.

[6] 刘小宁，刘岑，刘兵，等.密封螺栓的模糊许用可靠度与安全系数[J].现代制造工程，2014（10）：134－137.LIU Xiaoning，LIU Cen，LIU Bing，et al.Safety factor of seal bolt based on fuzzy allowable reliability[J].Modern Manufacturing Engineering，2014（10）：134－137.

[7] 刘小宁，刘岑，吴元祥，等.超高压圆筒形容器爆破压力计算公式的比较[J].机械强度，2015，37（2）：373－376.LIU Xiaoning，LIU Cen，WU Yuanxiang，et al.Burst pressure caculation formula compare of super－high pressure cylinder vessel[J].Journal of Mechanical Strength，2015，37（2）：373－376.

[8] 游涛，刘兵，袁小会，等.基于可靠性研究的内压薄壁容器两个重要系数[J].工业安全与环保，2014，40（6）：40－43.YOU Tao，LIU Bing，YUAN Xiaohui，et al.Two important factors of internal pressure thin－walled vessel based on reliability research[J].Industrial Safety and Environ－mental Protection，2014，40（6）：40－43.

[9] 张红卫，刘兵，刘岑，等.压力容器概率安全评定的可靠指标研究[J].河北科技大学学报，2011，32（2）：192－196.ZHANG Hongwei，LIU Bing，LIU Cen，et al.Reliable index research on pressure vessel probability safe evaluation[J].Journal of Hebei University of Science and Technology，2011，32（2）：192－196.

[10]刘小宁，潘传九，刘岑，等.钢制内压容器安全系数与试验压力系数研究[J].河北科技大学学报，2011，32（4）：321－325.LIU Xiaoning，PAN Chuanjiu，LIU Cen，et al.Research on safety factor and test pressure coefficient of steel wall intrinsic pressure vessel[J].Journal of Hebei University of Science and Technology，2011，32（4）：321－325.

[11]刘小宁，张红卫，刘岑，等.钢制压力容器静强度可靠性设计研究[J].机械设计与研究，2010，26（6）：138－145.LIU Xiaoning，ZHANG Hongwei，LIU Cen，et al.Study on reliability design of static strength for steel pressure vessels [J].Machine Design ＆Research，2010，26（6）：138－145.

[12]郑津洋，王珂，黄泽，等.液氮温度下奥氏体不锈钢强度试验研究[J].压力容器，2014，31（8）：1－6.ZHENG Jinyang，WANG Ke，HUANG Ze，et al.Study on strength of austenite stainless steel under liquid－nitrogen temperature[J].Pressure Vessel Technology，2014，31（8）：1－6.

[13]刘智敏.误差与数据处理[M].北京：原子能出版社，1981.

[14]化学工程手册编辑委员会.化工应用数学[M].北京：化学工业出版社，1983.

[15]刘小宁，刘岑，张红卫，等.单层与多层球形容器爆破压力的概率分布[J].武汉工程大学学报，2015，37（7）：49－54.LIU Xiaoning，LIU Cen，ZHANG Hongwei，et al.Probability distribution of burst pressure in single－layer and multi－layer spherical vessel[J].Journal of Wuhan Institute of Technology，2015，37（7）：49－54.

Research of tensile strength distribution of austenitic stainless steel S30408

LIU Cen，WU Yuanxiang，LIU Bing，YUAN Xiaohui，CHEN Gang，LIU Xiaoning
（School of Mechanical Engineering，Wuhan Polytechnic College of Software and Engineering，Wuhan，Hubei 430205，China）

Research of steel tensile strength distribution is the foundation of mechanical strength reliability design.Based on 60 sets of test data of the tensile strength of S30408at liquid nitrogen temperature（－196℃），with the method of mathematical statistics，the validity of the tested data and the distribution of tensile strength is researched.The results show that：1）when one－sided confidence is 99%，the 60sets of test data contains 1set of invalid data；2）when significance level is 0.05，the tensile strength is a random variable generally conforming to normal distribution；3）the influence of invalid test data to steel tensile strength distribution can not be ignored.

mechanical strength；austenitic stainless steel；S30408；tensile strength；validity；distribution

1008－1534（2016）01－0031－04

TH49；O213.2

A

10.7535／hbgykj.2016yx01006

2015－09－19；

2015－10－28；责任编辑：王海云

湖北省教育厅科研项目（B2014209）；武汉市创新人才开发资金资助项目

刘 岑（1989—），女，湖北武汉人，硕士，主要从事机械结构的可靠性与故障检测方面的研究。

刘小宁教授。E－mail：lxngjxy＠163.com

刘 岑，吴元祥，刘 兵，等.奥氏体不锈钢S30408抗拉强度分布规律研究[J].河北工业科技，2016，33（1）：31－34.

LIU Cen，WU Yuanxiang，LIU Bing，et al.Research of tensile strength distribution of austenitic stainless steel S30408[J].Hebei Journal of Industrial Science and Technology，2016，33（1）：31－34.