基于CPSO的基础设施模糊投资组合优化模型

曾 梅，郭均鹏（天津大学管理与经济学部，天津 300072）

基于CPSO的基础设施模糊投资组合优化模型

曾 梅，郭均鹏
（天津大学管理与经济学部，天津 300072）

针对基础设施效益模糊、难以度量的特点，结合模糊集理论，建立了模糊投资组合优化模型，改进粒子群算法，加入混沌思想，使用混沌粒子群算法（CPSO）求解基础设施的模糊投资组合优化模型。以4个城市投资公司的数据为样本，验证该方法的科学性与有效性。研究结果表明：模糊投资组合优化模型可较好地表征基础设施的模糊效益，提高基础设施投资决策的科学性；混沌寻优思想改进的粒子群算法可求得模糊投资组合优化模型的全局最优解，增强算法的鲁棒性。

组合最优化；模糊集；投资组合优化；混沌粒子群算法；模型；基础设施

投资组合优化模型可在政府资金规模有限的情况下，达到合理安排基础设施投资，最大化资金使用效率，提高投资决策科学性的目的。SUKSONG－HONG等[1]设计了多目标遗传算法解决电力基础设施的投资组合优化问题。CURA[2]通过比较粒子群算法和遗传算法、模拟退火算法、禁忌搜索算法，提出粒子群算法更适合处理低风险的投资组合优化问题。周君等[3]使用Markowitz投资组合理论研究农村基础设施的投资效率问题。郭莉等[4]通过分析电网企业的综合效益，探讨电网分布的最优规划。崔红卫等[5]通过EPB投资组合优化法，探讨了城市轨道交通及其关联项目之间的投资优化组合方案。廖青虎等[6]采用Logistic法分析公共文化服务设施项目的投资优化问题。HOBERG等[7]通过模拟退火算法计算基础设施的最优边际投资组合方案。LIN等[8]采用异质数据算法，求解基础设施项目最优投资组合方案。

以上研究为本文的研究奠定了基础，但是以往学者关于基础设施投资组合优化模型的研究还有以下不足：1）投资组合优化模型最优值的计算建立在效益的准确估算基础上，但是，基础设施的效益（尤其是其中的社会效益、环境效益）具有模糊性，难以准确度量；2）以往求解投资组合优化模型的粒子群算法、遗传算法、模拟退火算法等所求得的最优解都为局部最优解，而非全局最优解。基于此，本文将模糊集理论引入到基础设施效益的估算中，构建基础设施的模糊投资组合优化模型，并引入混沌思想，改进粒子群算法，提出混沌粒子群算法，求解基础设施的模糊投资组合优化模型的全局最优解。

1　模型的建立

1.1问题描述

假设某地方政府有n个基础设施需要投资，政府打算在初期t0期对资金在n种基础设施中进行分配。假设ri，t为t期基础设施获得的单位效益（包括经济效益、社会效益以及环境效益），ri，t为模糊数。政府在有限计划时间（t＝1，2，…，T）内进行T次投资，ri，t为r期投资对基础设施的投资比例，ui，t，li，t分别为ri，t的上、下界，xt＝（r1，t，r2，t，…，rn，t）为t期的投资组合。Rt为t期投资的总收益，Ci，t是t期投资中基础设施i的交易费用率，RN，t为扣除交易费用后的净收益。zi，t为决策变量，若zi，t＝1，则政府对基础设施i投资；若zi，t＝0，则政府不对基础设施i投资。kt为t期政府确定投资的基础设施数量。

1.2基础设施效益的模糊性

基础设施投资会受到政策、社会、环境等因素的影响，在短时间内，理性的政府投资者倾向于寻求满意解而不是最优解。根据ZADEH[9]提出的模糊集理论，设存在三角模糊数A＝（a，α，β），其隶属度函数可以表示为

根据CARLSSON等[10]的研究方法，在γ水平截集下，A的可能性均值、可能性方差以及其与的协方差定义为

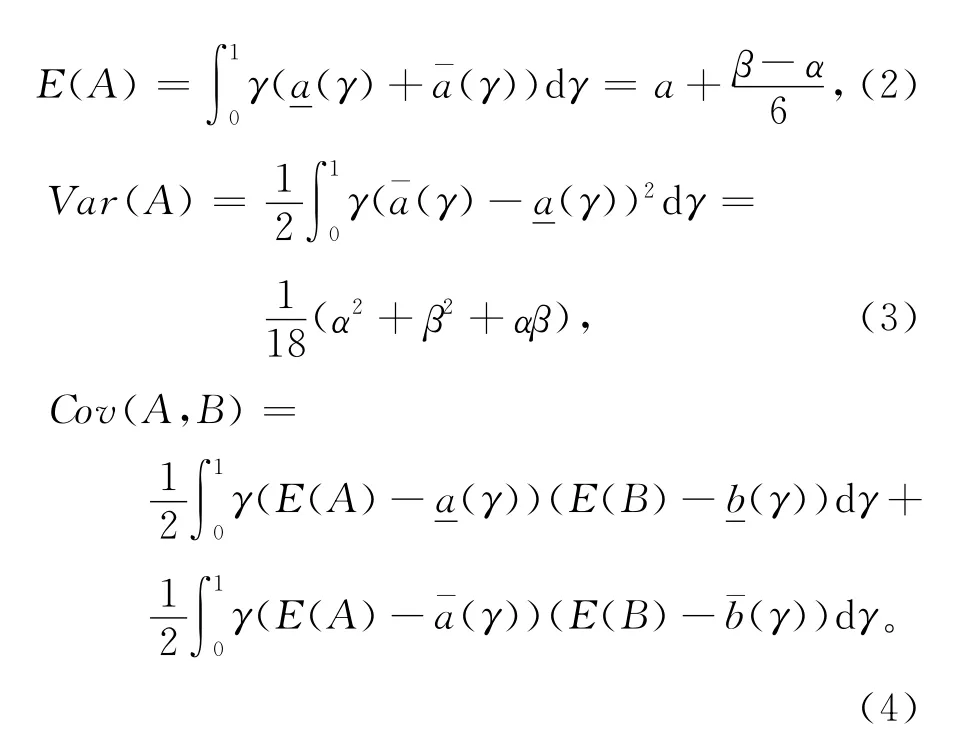
下文用式（2）－式（4）表示基础设施效益的模糊性。

1.3基础设施的模糊投资组合优化模型

基础设施i在第t期获得的单位效益ri，t可记为。按照GUERRA等[11]的计算方法，根据式（2）－式（4），本文可以计算出投资组合的模糊收益扣除交易费用Ct后的净收益RN，t、风险Var（Rt）分别为

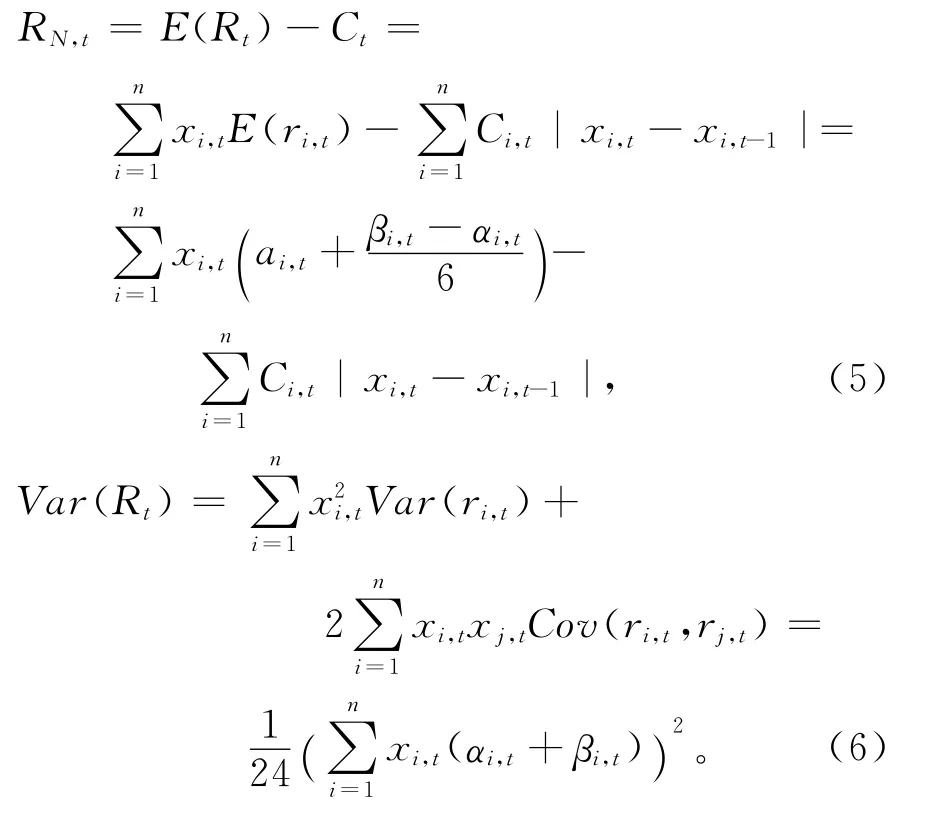
假设在一定时期内，政府对基础设施i进行了T次投资，每次投资额度为一单位，则T次投资后能得到的累积收益ARt和累积风险AVart分别为

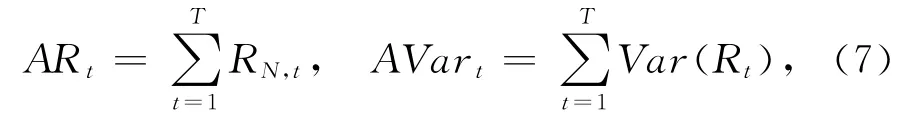
假设政府投资者为追求效益最大、风险最小的理性投资者，根据式（6）与式（7）中的收益、风险公式，本文建立基础设施的模糊投资组合规划问题如式（8）所示：

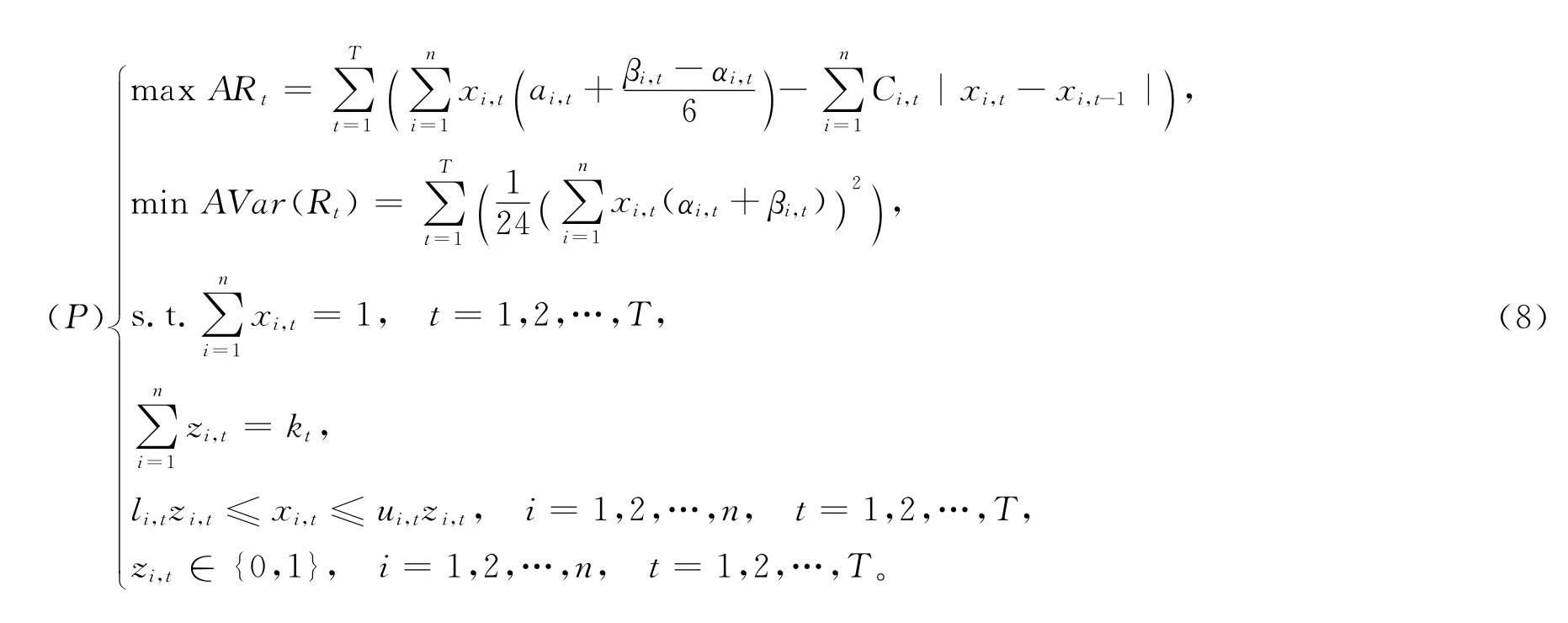
1.4混沌粒子群算法的提出

粒子群算法（particle swarm optimization，PSO）具有参数少、运算简单、收敛速度快的优点，常用来解决非线性、多极点、不可微、多变量的复杂优化问题。然而，由于PSO是属于有导向的随机性启发式算法[12－13]，在求解复杂优化问题时，存在易陷入局部最优点、后期收敛速度慢，鲁棒性较差等缺点[1416]。本文针对线性规划式（8）中基础设施模糊投资组合优化的特点，充分利用PSO的特点以及混沌运动遍历性的特点，引出了一种混沌粒子群优化算法，一方面处理基础设施效益的模糊性，另一方面求解全局最优解。

在粒子群优化算法中，每一个粒子代表最优问题的一组潜在的解，各个粒子通过自身的“认知”和群体之间的“交流”来实现最优值的求解。每个粒子更新当前速度和位置方程为

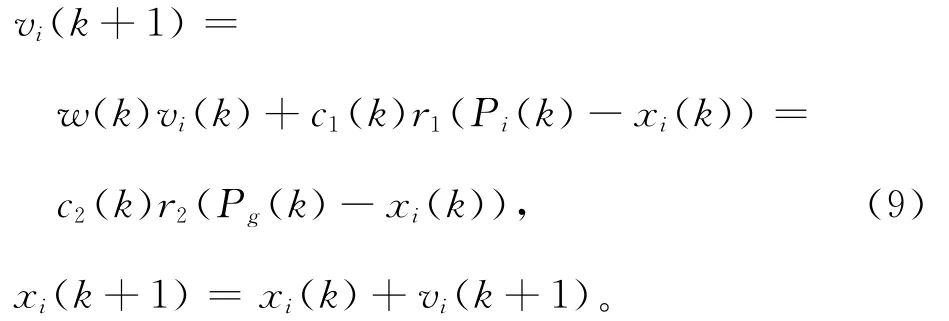
式中：k为当前迭代数；vi（k）和xi（k）为第i个粒子的速度和位置；w（k）为粒子速度更新的惯性系数；c1（k）和c2（k）为粒子的学习因子；r1和r2是介于[0，1]的随机数；Pi（k）为粒子i第k次迭代的最优位置；Pg（k）为粒子群第k次迭代的最优位置。

基本粒子群算法易陷入局部最优，需要提高粒子的全局搜索能力。文献[8]提出了一种正弦混沌映射，但其往往不能保持与模型中的xi，t范围的一致性，本文将文献[8]中的正弦混沌映射修正为

zi＋1＝｜sin（5.65／zi）｜， 0＜zi≤1。（10）

式中zi为混沌变量序列，式（10）比文献[8]的优越之处在于增加了绝对值符号，从而可保证正弦混沌映射与xi，t的范围一致。

具体来说，本文所提出的混沌粒子群优化算法的步骤如下。

Step2：按照基本粒子算法的更新式（9），更新粒子的速度和位置。

Step3：混沌优化粒子群的最优位置。

1）将最优值映射到正弦混沌映射的定义域

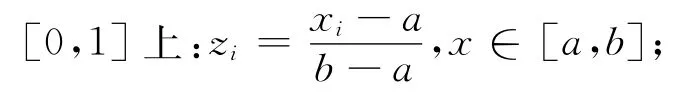
3）通过方程xi＝a＋（b－a）yi求解，确定混沌序列变量

Step5：满足最优条件或者达到最大迭代次数时，停止迭代，否则，返回Step2。

2　实证分析

本文选取天津市城市基础设施建设投资集团有限公司、上海市城市建设投资开发总公司、北京市基础设施投资有限公司、重庆市城市建设投资（集团）有限公司这4个城投公司为样本。针对本文提出的基础设施模糊投资组合优化模型，使用本文所改进的混沌粒子群算法，求解该算法的科学性与有效性。为保证数据的可获得性与完整性，本文选取以上4个公司的上市子公司进行研究，分别是天津创业环保集团股份有限公司（股票代码：600874）、京投银泰股份有限公司（股票代码：600683）、上海市城投控股股份有限公司（股票代码：600649）、重庆市渝开发股份有限公司（股票代码：000514）。

本文提取了这几家公司从2001年1月到2015 年1月期间周开盘价与周收盘价的历史数据进行分析，根据式（1），利用（周收盘价－周开盘价）／周开盘价，得到了这14年期间的周模糊历史收益率，本文以2年为1个周期（共7个周期）对其进行分析，具体数据如表1所示。

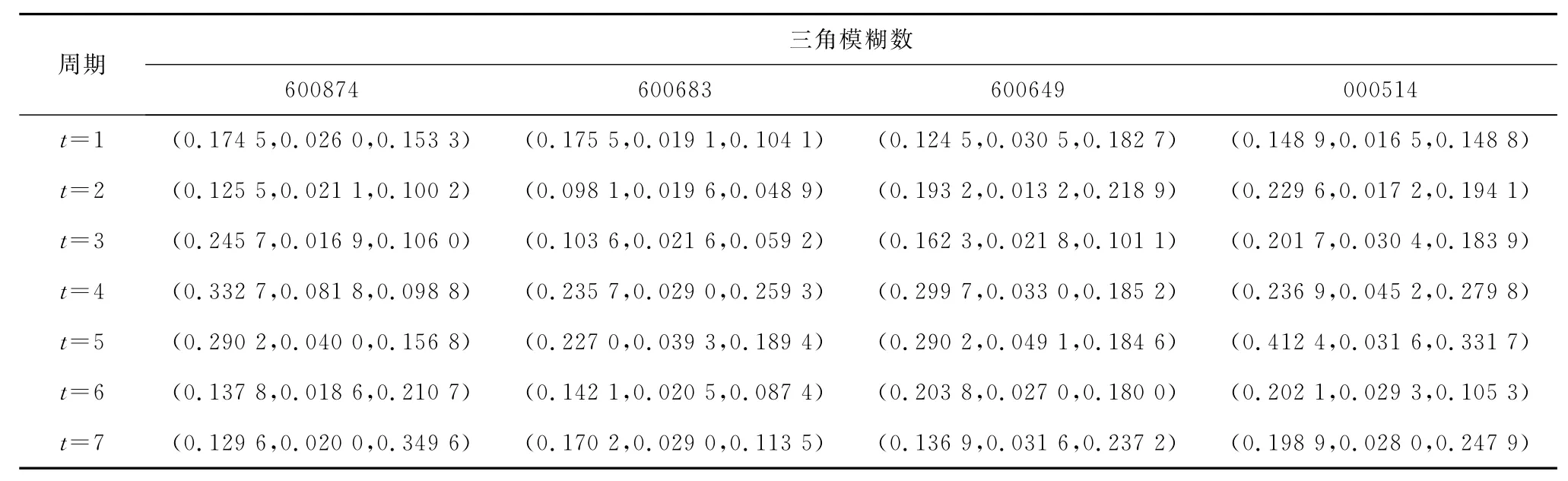
表1　股票收益率的三角模糊数Tab.1 Triangular fuzzy number of return rate

在中国证券市场上，股票的交易费用主要分为印花税和佣金2种，本文假定股票的交易费用率为5‰。对于上述问题，利用本文所设计的混沌粒子群进行计算。仿真实验时设定粒子群规模为50；最大迭代次数为1 000次；为了控制粒子速度的变化范围，设定了粒子速度的取值范围为[0，0.5]；经过1 000次迭代后进行混沌粒子群算法（CPSO）与粒子群算法（PSO）的比较，计算结果如表2所示。

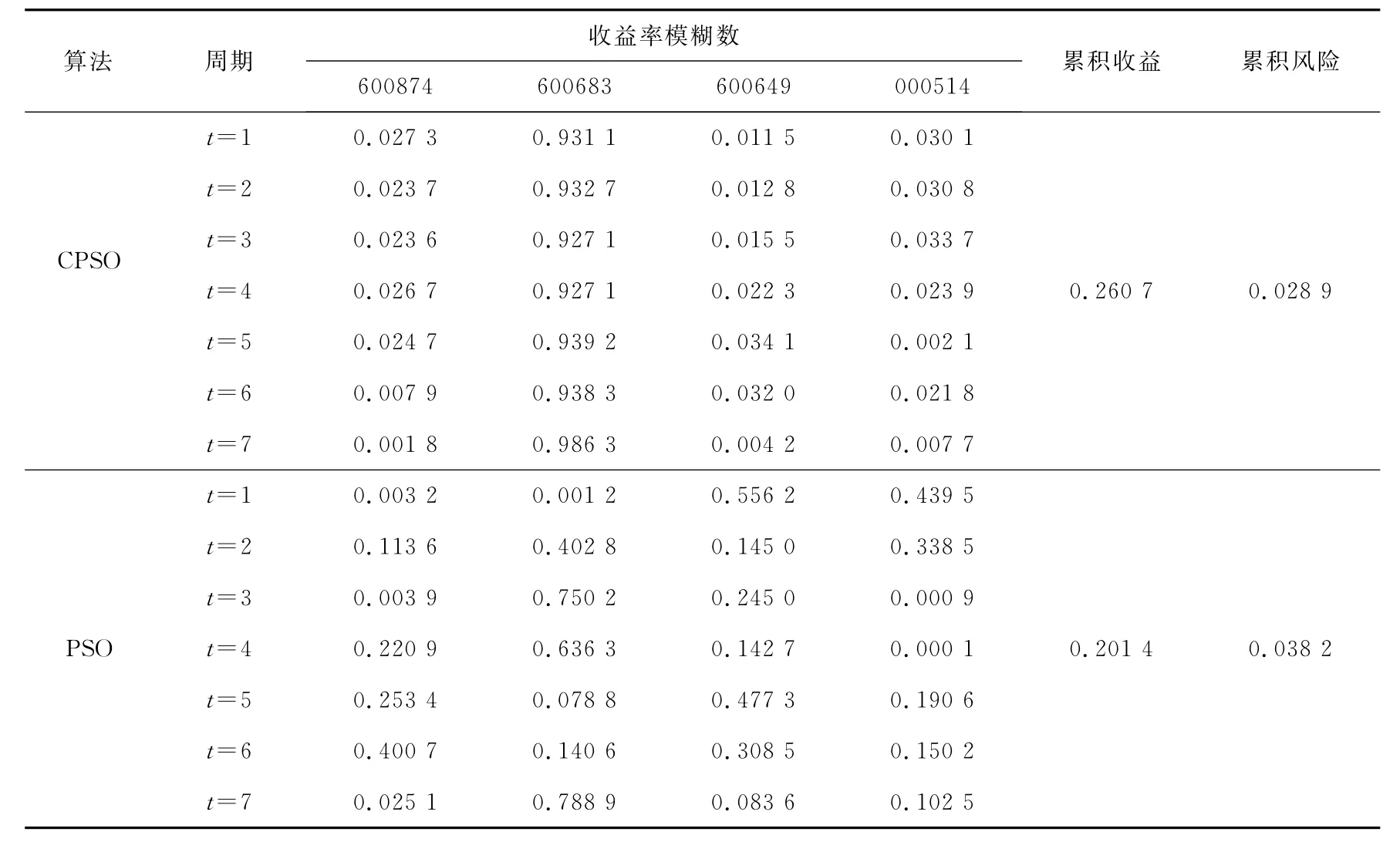
表2　混沌粒子群算法与粒子群算法的结算结果比较Tab.2 Comparison of computational results between CPSO and PSO

由表2可知，利用混沌粒子群算法得到的结果表示：投资方在第1期按2.73%，93.11%，1.15%，3.01%的比例分别分配到代码为“600874”，“600683”，“600649”，“000514”的股票中去。同理，第2期投资比例为2.37%，93.27%，1.28%，3.08%，以此类推，经过7期的累积投资，最终可以得到0.260 7的累积收益和0.028 9的累积风险。与粒子群算法相比，同样按照表2中的方式进行分配，可发现累积收益下降到了0.201 4，累积风险提高到了0.038 2。由此可看出，混沌粒子群算法提高了寻优的遍历性，跳出局部解，找到投资组合优化模型的最优解。

3　结 论

由于基础设施效益难以准确度量，本文使用模糊数表征基础设施效益，建立模糊收益最大、风险最小的投资组合优化模型。考虑到粒子群算法容易陷入局部最优，对基本粒子群算法进行改进，加入了混沌寻优思想，利用混沌粒子群算法求解，并以4个城投公司的数据证明该方法的有效性。实证分析表明，基础设施的模糊投资组合优化模型可较好地表征基础设施的模糊效益，有利于提高基础设施投进的粒子群算法，可求得基础设施模糊投资组合优化模型的全局最优解。

／References：

[1] SUKSONGHONG K，BOONLONG K，GOH K L.Multiobjective genetic algorithms for solving portfolio optimization problems in the electricity market[J].International Journal of Electrical Power and Energy Systems，2014，58（2）：150－159.

[2] CURA T.Particle swarm optimization approach to portfolio optimization[J].Nonlinear Analysis Real World Applications，2009，10（4）：2396－2406.

[3] 周君，周林.新型城镇化背景下农村基础设施投资对农村经济的影响分析[J].城市发展研究，2014，21（7）：14－17.ZHOU Jun，ZHOU Lin.Analysis of the effects of rural infrastructure investment on the rural economy based on new－type urbanization[J].Urban Development Studies，2014，21（7）：14－17.

[4] 郭莉，付立思.含分布式发电配电网企业综合效益分析[J].河北工业科技，2014，31（6）：463－468.GUO Li，FU Lisi.Comprehensive benefits analysis of power grid enterprises with distributed generation network[J].Hebei Journal of Industrial Science and Technology，2014，31（6）：463－468.

[5] 崔红卫，王伟，曾鹦.轨道交通建设项目EPB投资组合优化模式研究[J].软科学，2015，29（8）：129－134.CUI Hongwei，WANG Wei，ZENG Ying.Research on EPB portfolio optimization mode of rail transit construction project [J].Soft Science，2015，29（8）：129－134.

[6] 廖青虎，陈通，孙钰.我国公共文化设施边际融资的最优选择[J].财经论丛，2015（9）：42－49.LIAO Qinghu，CHEN Tong，SUN Yu.The optimal marginal financing choice of public cultural facilities[J].Collected Essays on Finance and Economics，2015（9）：42－49.

[7] HOBERG G，PHILLIPS G，PRABHALA N.Product market threats，payouts，and financial flexibility[J].Social Science Electronic Publishing，2012，69（1）：293－324.

[8] LIN C，MA Y，MALATESTA P.Corporate ownership structure and the choice between bank debt and public debt[J].Journal of Financial Economics，2012，109（2）：517－534.

[9] ZADEH L A.Fuzzy sets[J].Information and Control，1965，8（3）：338－353.

[10]CARLSSON C，FULLER R.On possibilistic mean value and variance of fuzzy numbers[J].Fuzzy Sets and Systems，1999，122：315－326.

[11]GUERRA M L，STEFANINI L.Approximate fuzzy arithmetic operations using monotonic interpolations[J].Fuzzy Sets and Systems，2005，150（1）：5－33.

[12]陈如清，俞金寿.混沌粒子群混合优化算法的研究与应用[J].系统仿真学报，2008，20（3）：685－688.CHEN Ruqing，YU Jinshou.Study and application of chaos－particle swarm optimization－based hybrid optimization algorithm[J].Journal of System Simulation，2008，20（3）：685－688.

[13]张健，朱旭东，王真.一个新的动态约束因子PSO算法[J].河北工业大学学报，2010，39（3）：51－55.ZHANG Jian，ZHU Xudong，WANG Zhen.A new dynamic constrain factor particle swarm optimization algorithm[J].Journal of Hebei University of Technology，2010，39（3）：51－55.

[14]王越，曾晶，董丽梅，等.基于粒子群的BP神经网络算法在猪等级评定中的应用[J].重庆理工大学学报（自然科学版），2013，27（1）：37－41.WANG Yue，ZENG Jing，DONG Limei，et al.Study on pork grade evaluation of BP neural network based on PSO[J].Journal of Chongqing Institute of Technology（Natural Science），2013，27（1）：37－41.

[15]季香君，马立红，刘紫玉.流水工序调度与生产效率的关系模型分析[J].河北工业科技，2014，31（4）：291－295.JI Xiangjun，MA Lihong，LIU Ziyu.Relational model analysis of assembly line scheduling and efficiency[J].Hebei Journal of Industrial Science and Technology，2014，31（4）：291－295.

[16]张泽星.混合邻域结构的粒子群算法[J].河北工业科技，2015，32（3）：219－223.ZHANG Zexing.A PSO algorithm based on mixture neighborhood structure[J].Hebei Journal of Industrial Science and Technology，2015，32（3）：219－223.

Fuzzy optimized investment portfolio model on infrastructure based on chaos particle swarm optimization

ZENG Mei，GUO Junpeng
（College of Management and Economics，Tianjin University，Tianjin 300072，China）

Aiming at the vague benefit and hard measurement of infrastructures，combining with the fuzzy set theory，the aper formulates an optimized investment portfolio model，then improves the particle swarm optimization by involving fuzzy hinking，and uses the chaos particle swarm optimization（CPSO）to obtain the fuzzy optimized investment portfolio model of nfrastructures.With data samples of the investment companies from four cities，it testifies the scientificity and effectiveness of haos particle swarm optimization.The result shows that the fuzzy optimized investment portfolio model can better character he fuzzy benefit of infrastructures，improving the scientificity of decision－making in infrastructure investment，and the chaos ptimization method used for improvement of particle swarm method can help obtain the globally optimal solution fuzzy ptimized investment portfolio model，and enhance the robustness of the algorithm.

combinational optimization；fuzzy set；optimized investment portfolio；chaos particle swarm optimization；model；infrastructure

1008－1534（2016）01－0001－05

F270.5；O242.1

A

10.7535／hbgykj.2016yx01001

2015－09－22；

2015－11－16；责任编辑：张 军

国家自然科学基金（71271147）

曾 梅（1971—），女，海南澄迈人，博士研究生，主要从事管理科学方面的研究。

郭均鹏教授。E－mail：liaoqinghu＠163.com

曾 梅，郭均鹏.基于CPSO的基础设施模糊投资组合优化模型[J].河北工业科技，2016，33（1）：1－5.

ZENG Mei，GUO Junpeng.Fuzzy optimized investment portfolio model on infrastructure based on chaos particle swarm optimization[J].Hebei Journal of Industrial Science and Technology，2016，33（1）：1－5.