义务教育年限延长的模拟研究：学龄人口预测视角*

薛耀锋，杨棋雯，顾小清①

(1.华东师范大学 教育信息技术学系，上海 200062；2.华东师范大学 课程与教学系，上海 200062)

义务教育年限延长的模拟研究：学龄人口预测视角*

薛耀锋1，杨棋雯2，顾小清1①

(1.华东师范大学 教育信息技术学系，上海 200062；2.华东师范大学 课程与教学系，上海 200062)

“是否需要延长义务教育年限以及如何延长”这一教育政策的制定，是需要涉及到社会经济、文化、人口等复杂系统中的诸多因素的决策行为，是借助计算机模拟技术为教育决策提供支持的典型应用。该文聚焦于决策支持系统的预测模型，以展现决策模拟支持系统如何通过模型设计和计算机模拟技术的应用实现对决策的支持；基于人口预测的视角，采用LESLIE人口模型对我国基础教育的学龄人口未来发展趋势进行预测，根据计算机模拟预测2016-2025年的学龄人口变化趋势，为决策提供依据。

义务教育年限；基础教育；人口预测；LESLIE模型

一、引言

基于数据的教育决策在教育技术快速发展的近30年间越发成为该领域体现潜能和优势的研究方向[1]。利用计算机的计算能力进行数据的分析并提供决策支持的思想在计算机技术发展的早期就已形成。随着教育决策涉及的复杂性日益凸显，教育决策科学化的需求对基于计算机的决策的依赖也越发突出。比如，针对是否需要延长义务教育的年限、以及如何延长的问题，由于涉及到人口、经济投入等诸多复杂因素，如何借助计算机模拟的方式为决策提供依据，也就成为一个迫切需要解决的问题。

1986年4月我国颁布了《中华人民共和国义务教育法》，标志我国义务教育用法律形式固定下来，义务教育从刚开始的低水平逐渐发展至今其普及率和质量达到较高水平。随着我国国民经济的快速发展，政府对教育经费的财政支持力度不断增加，我国正从教育大国向教育强国转变，在此背景下，有专家提出我国应逐步实现12年义务教育，其中北京和深圳等经济发达地区率先尝试延长义务教育年限[2][3]。但是也有研究表明，延长义务教育年限不可冒进[4][5]。近几年关于义务教育年限延长之争备受关注，有研究认为经济因素、人口状况、国家传统、法律准备是影响义务教育年限的四大主要因素。但是，有关我国是否已经满足义务教育延长条件的争论大多基于经验，而缺乏具体数据支撑，让数据说话在教育决策中能够使得相关决策有据可依[6]。因此，预测义务教育常规学段，义务教育向下延伸学段(幼儿园)和向上延伸学段(高中)学龄人口的变化和趋势对研究义务教育年限延长有着深远意义。

人口的数量、结构及其变动，会给教育带来直接而深刻的影响，其中学龄人口变动对义务教育的影响更是长远而深刻。不少研究指出，部分地区，特别是农村地区出现的生源多余或缺乏已成为当前困扰各类学校生存和发展的普遍性难题[7-9]。预测义务教育学龄人口变动对各级各类教育部门的决策具有重要指导意义。目前，义务教育问题的研究热点开始转向不同的义务教育年限延长方案的研究[10][11]。义务教育年限向高中学段延长还是向幼儿园学段延长，对高中学段和幼儿园学段学龄人口规模预测为此难题的解决提供了有力的决策支持和参考。同时，我们也要认识到，对人口规模预测分析需结合当前二胎政策对人口结构带来的影响，对教育决策的支持才更精确。

本文以全国第六次人口普查数据和2010-2014年的人口历史数据为依据，采用LESLIE人口模型对我国基础教育的学龄人口未来10年发展趋势进行了预测，通过分析学龄人口变化趋势的特征，对我国义务教育资源配备与管理决策的影响做出分析，并提出了一些应对策略和建议。

二、学龄人口预测模型

学龄人口的变化趋势是影响义务教育年限政策的重要考量。在我们的模型中采用LESLIE人口预测模型对人口变化进行预测。目前国际上已发展形成众多成熟的人口预测模型，国内众多文献基于本国人口数据对一些模型进行了验证和优化研究，如曲线拟合[12-14]、GM(1,1)灰色预测模型[15-17]、基于BP神经网络预测模型[18]和Logistic模型预测模型[19]等。

但是，上述人口预测模型仅对总人数进行预测，其预测结果没有考虑人口结构，即没有提供不同年龄具体的人口预测数据。对于义务教育年限延伸方案学龄人口规模的分析，需要对幼儿园至高中不同阶段适龄年龄段的具体人口数量进行预测。上海幼儿园学龄段为3到5岁，小学和初中学龄段为6到14岁，高中学龄段为15到17岁；而全国与其他省市的幼儿学年龄段为4到6岁，初中学年龄段为7到15岁，高中学年龄段为16到18岁。本文采用LESLIE模型对义务教育年限延伸方案中不同阶段学龄人口进行预测。LESLIE模型是由澳大利亚学者LESLIE提出的一种分析动物种群数量变化的数学模型，现在一般多用于以年龄及性别为机理的人口预测[20]。

LESLIE人口预测模型主要在于构造转移矩阵：

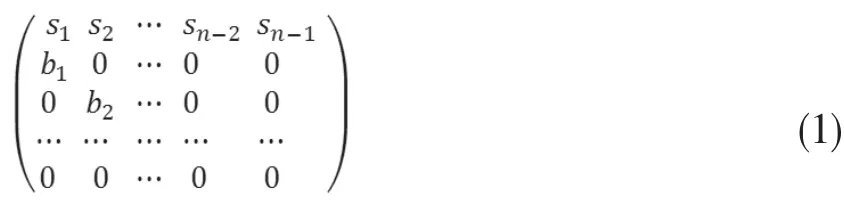
式(1)中，矩阵中sn代表生存率；bn代表生育率。LESLIE设定第i年某个年龄阶段的人口数就等于此年龄组上一个年龄段乘以对应的生存率。而第i年出生的新生婴儿数就等于各个年龄阶段的育龄妇女乘以对应的生育率。

本文基于LESLIE人口模型进行模拟预测不同年龄的人口数量。LIESLIE模型实际上是通过生育率和死亡率建立女性单项性别生命矩阵。

我们选取年龄间隔为1岁的分组，假设0-100岁(100岁以上也算作100岁)的不同年龄的初始人口数：

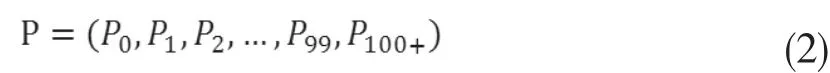
通过每个年龄段的死亡率构建100*100的存活矩阵：

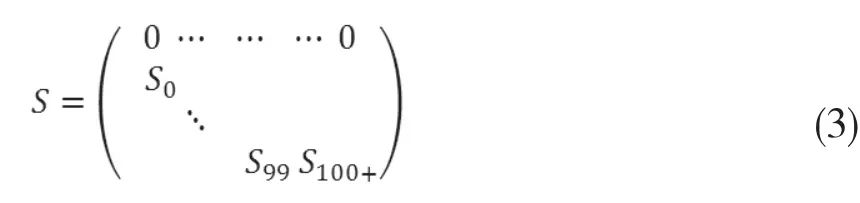
式(3)中矩阵中的S表示对应年龄段的存活率。那么P0S0为1年后0岁人口的存活率，作为1年后1岁人口的组成部分。同样，通过各年龄段的生育率，可以构建出100*100出生矩阵：

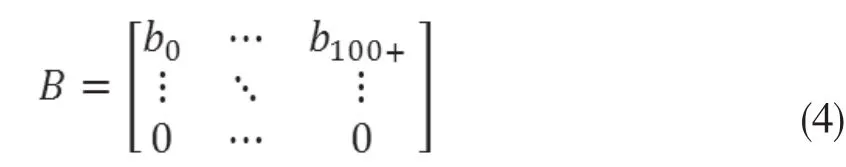
式(4)中，实际上矩阵中第一行向量中非0数据为15-49岁育龄妇女相对应的生育率，其他年龄的生育率均为0。根据S矩阵和B矩阵构建LESLIE矩阵，L=B+S:

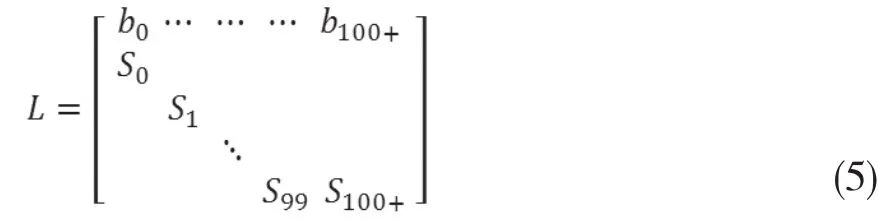
因此，1年后的预测人口为：

P(n+1)表示n+1年后的人口矩阵，L(n+1)为n+1年后的人口转移矩阵，P(n)为n年后的人口矩阵。当n=0时，P为初始的实际人口数；当n>0时，P为预测的人口矩阵。

三、学龄人口变化的计算机模拟

1.学龄人口模拟

本文以第六次全国人口普查数据为基础，以MATLAB软件为仿真平台，使用LESLIE人口预测模型分别对全国和各省市2010年到2025年人口预测数据进行仿真模拟，以验证这一模型的有效性，以便在决策系统中采用。

在我们的仿真过程中，人口预测初始数据源于第六次人口普查数据的每个年龄段的人数、死亡率和出生率，在MATLAB上编写预测人口运行代码，预测的部分结果如表1所示。

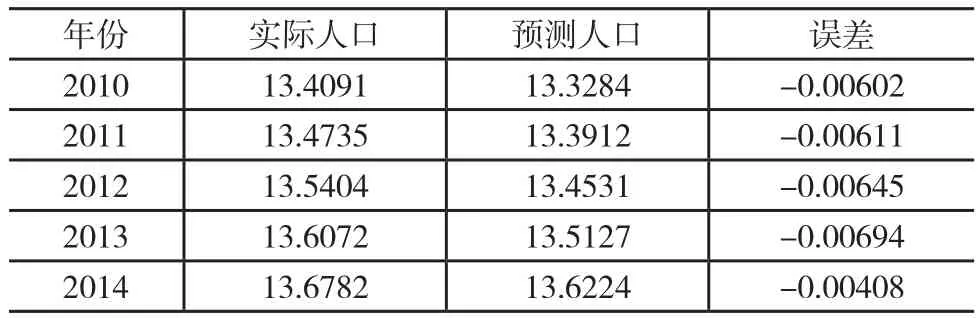
表1 2010-2014年全国人口总数预测结果(单位：亿人)

LESLIE人口预测算法的优势在于，比起其他人口预测算法，能够对年龄结构、生育率和死亡率等多种因素加以综合考虑，从而形成动态的发展预测系统。使用LESLIE预测算法可以得到预测年度的人口年龄分布图，预测人口老龄化等问题，也满足本文对预测各学龄阶段人口数量的需要。当然LESLIE模型也存在一定的误差，例如从表1看出预测的人口数比实际人口数量少， 全国预测误差在2013年达到最大，绝对值为0.00694。总体来说LESLIE人口预测模型对全国和各地区的预测效果均达到较好效果。

LESLIE预测误差主要源于模型将影响人口发展的重要参数生育率和死亡率定义为常量。比如在本文中，预测年的生育率和死亡率恒定为2010年的生育率与死亡率。但是随着政策和社会环境的改变，每年的生育率和死亡率并不是固定不变的。可以看出，LESLIE的预测结果的人口增长比实际人口增长速率要缓慢，可能是因为中国医疗和社会保障条件的不断改善、放开的二胎政策等影响，所以生育率有升高趋势。基于模型的静态建模的倾向，我们对原来LESLIE模型进行了改进，以全国人口为例对所测结果添加了修正系数。在MATLAB仿真平台下，求出实际人口数与预测人口数的误差平均数r，再加上LESLIE模拟预测的人口数，得到修正后的结果如表2所示。

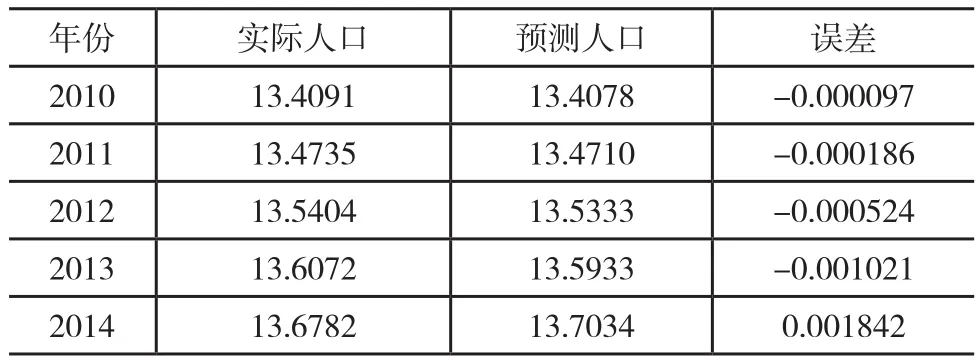
表2 修正后2010-2014年全国人口总数预测结果(单位：亿人)

从表2中可见，修正后的预测结果与实际人口数更接近。最大误差绝对值减少到0.001842。随着预测时间延长，实际数据比预测数据多的趋势仍然呈增长趋势。同时，各个人口结构分布的数据也需要做相应修正。本文中，我们假设总人口数变化的比率与每个年龄的变化比率一致。所以使用以下公式对每个年龄的预测人口数进行修正：

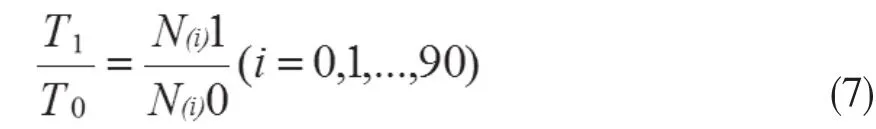
式(7)中，T1和T0分别表示修正后与修正前的总人口数，N(i)1和N(i)0分别表示第i年修正后与修正前的人口数。

2.预测结果比较

为检验LESLIE预测数据的效果，本论文使用多项式拟合方法预测2010-2025年的人口数据，再与LESLIE预测数据结果进行比较。

本文将多项式拟合方法预测结果与LESLIE模型的预测结果做比较，如表3和图1所示。

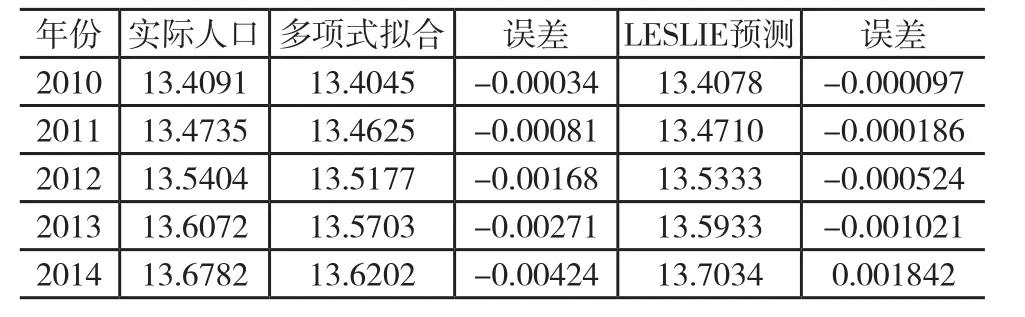
表3 2010-2014年多项式拟合与LESLIE预测结果比较

图1 2010-2014年多项式拟合与LESLIE预测结果比较

如图1所示，黑色直线表示2010-2014年全国人口实际总数量，黑色星号表示使用LESLIE预测的人口数量，黑色色菱形表示多项式拟合人口数量。从图1中可看出，LESLIE模型预测数据与实际人口数的差距要比多项式拟合预测数量与实际人口数的差距小得多。从表3可见，使用拟合预测人口，其最大误差绝对值为0.00424，且随着预测时间的延长，预测的误差不断增大，而LESLIE的预测误差变化较平稳，最大误差为0.001842，说明使用LESLIE预测人口数的准确度较高。

四、延长义务教育年限的学龄人口模拟

是否需要延长义务教育的年限，需要综合考虑学龄人口的变化趋势、社会经济和文化等诸多因素。在我们开发的决策支持系统中，主要将学龄人口、经济发展因素作为主要变量，通过系统模拟，提供给定的决策选项下面临的人口和经济情况。决策者可以对诸多因素选定不同优先级或者综合加以考虑，以审慎地制定相关政策。

在我们的模拟系统中，根据以上的学龄人口预测模型，决策支持系统根据全国第六次人口普查数据对全国和各省市2010年至2025年幼儿园、小学、初中和高中学龄人口进行了预测，为义务教育年限延长决策提供了人口因素的科学依据。下页图2-5分别为模拟决策系统模拟的2010-2025年全国幼儿园、小学、初中和高中学龄人口规模趋势图。

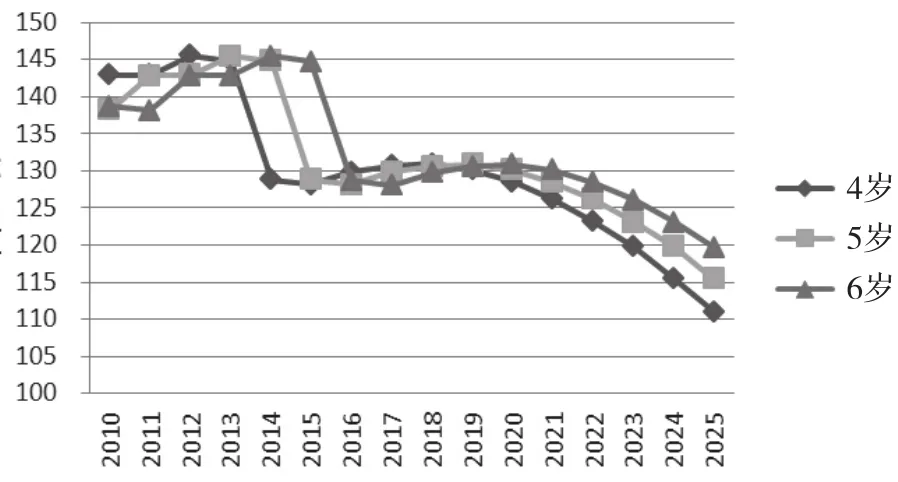
图2 幼儿园学龄人口趋势

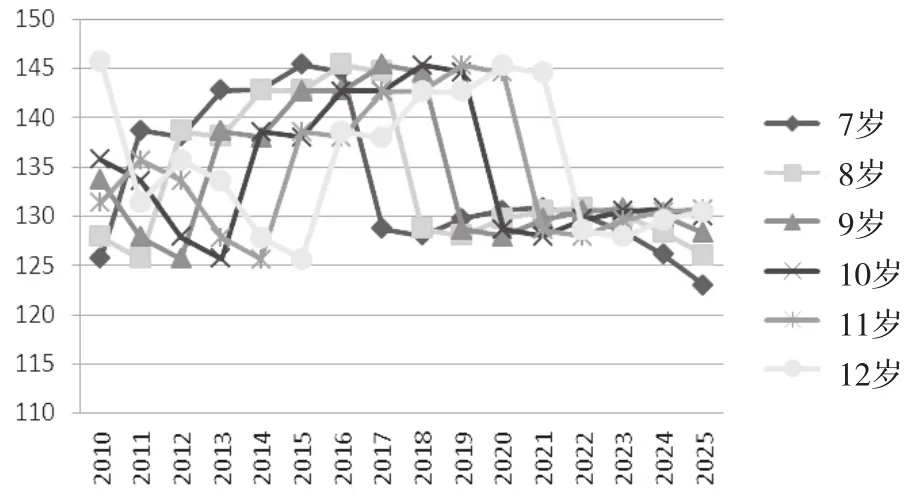
图3 小学学龄人口趋势

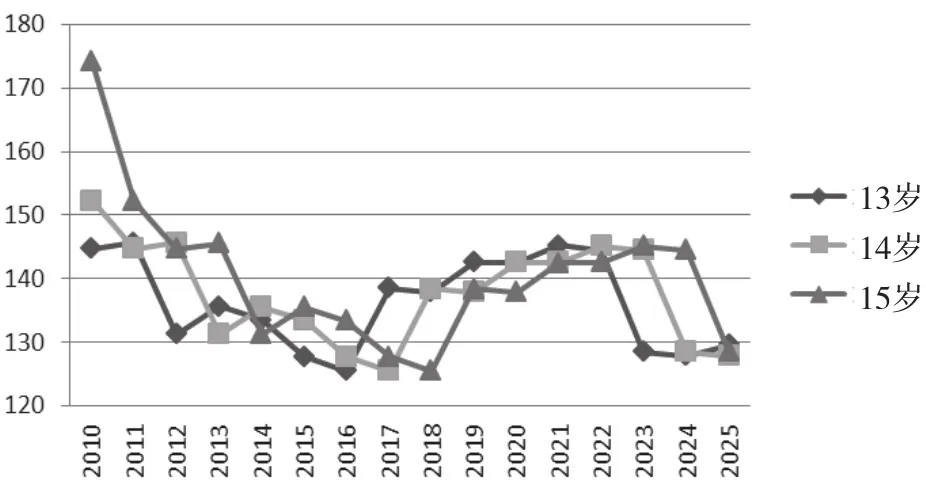
图4 初中学龄人口趋势

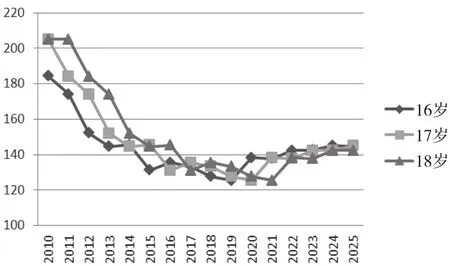
图5 高中学龄人口趋势

从图2-5可以看出，幼儿园、九年义务教育和高中阶段的学龄人口变化趋势各不相同，所以根据不同的变化趋势，对不同阶段教育的决策也应结合具体情况分别进行分析。

(一)学龄人口对现阶段教育的影响

自全国普及义务教育以来，提高义务教育的普及度和效度成为两个重要目标。《国家中长期教育改革和发展规划纲要(2010-2020年)》中提出“要巩固义务教育普及成果。适应城乡发展需要，合理规划学校布局，办好必要的教学点，方便学生就近入学”[21]。因此，在稳定推进义务教育普及的前提下，最理想的状态是各个地区的办学规模应随当地学生数量的变化而做调整，一方面保证学生都能有学校可上，另一方面实现老师资源的最优配置，以保障一些偏远地区的中小学校的生源和质量。例如，从图4可看出，从2010年到2017年全国初中阶段的学龄人口呈减少趋势，因此我们推测某些地区的生源下降，针对此情况，可以对特定地区采取撤出合并学校的方式来达到学校人口的平衡。从图2和图5可看出，2013年到2016年全国幼儿园和高中阶段学龄人口数也呈减少趋势，高中的减幅相对较大。因此，也可采用同样的方式来维持生源与学校之间的平衡。直到2017年，幼儿园和高中阶段的学龄人口变化趋势趋于平缓，2020年后，幼儿园阶段学龄人口继续缓慢减少。但是目前对中小学撤并学校的已有研究也提出新问题，东中西部地区学校撤并速度均超过学生减幅[22]。因此，学校的撤并速度应与人口的变化速率相适应，而预测学龄的人口变化趋势恰恰能够为学校撤并速率提供科学参考。同时，《国家中长期教育改革和发展规划纲要(2010-2020年)》要求“推进义务教育均衡发展”[23]，对于不同地区不同学龄人口变化的趋势，相关教育部门需要实现均衡发展这一战略性任务。根据学龄人口推进义务教育学校标准化建设，建立健全义务教育均衡发展保障机制，均衡配置教师、设备、图书、校舍等各项资源。例如，从图3可以看出，全国小学阶段学龄人口的发展趋势比较复杂，呈现“先减少—后增长—再减少”的趋势。针对于此，国家对小学阶段每年的教师和其他方面的配置都需要提供特殊介入，以确保教师以及其他资源与相应的学龄人口相平衡。同样，国家对于小学阶段每年的经济投入也应做相应调整。如果一些年份的学龄人口数量处于波谷与波峰时，在波谷年与波峰年的教育生均经费保持不变的情况下，此年的教育经费投入可根据人口变化适当减少或增加。由此可见，人口预测在一定程度上能够为教育决策做出有力支撑。

使用LESLIE预测人口的问题假设之一是，预测期内社会比较稳定，人口平稳发展，人口数量不会出现大的动荡起伏。因此，短期内人口的生育率与死亡率的总体水平可看视为常数[24]。而二胎政策的全面开放，会促进妇女生育率升高，促使新生儿数量在一定程度上增加，所以在参考LESLIE预测数据的同时应结合二胎政策对人口发展带来的一系列影响，而二胎政策是否会平衡我国人口减少的趋势还有待考察。

(二)学龄人口对义务教育年限延长的影响

第一，学龄人口数量的变化对义务教育的影响深远，目前研究中主要存在两种主流的义务教育年限延长方案：向上延长与向下延长[25]。向上延长即为将高中纳入义务教育的范围；向下延长即为将幼儿园纳入义务教育的范围。关于我国是否已经具备延长义务教育条件的争论也十分激烈，各专家的观点和研究结果也不一致。但大多数专家一致认为，国家的经济实力是决定义务教育年限是否延长的最主要因素[26]。《国家中长期教育改革和发展规划纲要(2010-2020年)》明确说明“优化国家财政性教育经费，使按在校学生人数平均的教育费用逐步增长，保证教师工资和学生人均公用经费逐步增长”[27]。因此，人均GDP在义务教育投入方面起到重要作用，人均GDP越高，该国的经济实力越强，其在教育经费上面的潜在投入就越多。结合人口规模来看，一个国家人口越多，在相同经济收入情况下，人均GDP就越小，教育经费的潜在投入方面能力下降，对教育建设的负担加重，此时，在同等质量的教育环境下，国家实行义务教育的年限就会减少。根据模拟决策系统的推算，在2010至2015年期间，全国人口的增长趋势缓慢，每年的增长速率递减。因此，从人口规模上来看，在我国GDP平稳增长的情况下，我国人均GDP不会大幅度下降。由此，学龄人口预测对义务教育延长决策中的教育经费投入提供了有效的数据支撑。

第二，学龄人口规模的发展趋势必定对教育决策产生影响。关于我国义务教育是否达到延长的条件并非仅仅关乎教育经费投入的多少。除此以外，当前义务教育的质量是决定我国义务教育发展的重要因素。《国家中长期教育改革和发展规划纲要(2010-2020年)》提出“提高义务教育质量。建立国家义务教育质量基本标准和监测制度”[28]。决策模拟系统的学龄人口预测数据可以让我们推算出不同学龄段已完成和未完成义务教育的人口数量。对于未完成义务教育的学生，他们已构成为社会劳动力的一部分，但是由于其受教育程度较底，他们是否会对社会的经济效应与社会稳定产生一定的负面影响还待进一步研究。九年义务教育的普及度是义务教育年限是否延长的重要指标之一。通过观察、分析与借鉴九年义务教育的实施情况，可以分别预测向上延长或向下延长所带来的社会效应，并对义务教育年限延长的决策进行再思考。

第三，对学龄人口的预测在一定程度上可以预测教师队伍的发展规模。跟据国家教育督导报告，我国教师总体配置的生师比逐步下降[29]。到2013年，全国小学的生师比为16.76:1，初中生师比为12.76:1，高中的生师比为14.59:1。因此，决策模拟系统通过预测学龄人口数量，可以进一步预测义务教育年限延长对师资力量的需求程度，推断目前的教师队伍是否满足义务教育年限延长之后的办学条件。

值得注意的是，在义务教育年限是否延长的有关文献中，很少提及二胎生育政策对此带来的影响。有研究表明，二胎政策实施后的短期内，我国可能会出现小的生育回潮，新生婴儿增多。但总体而言，该政策对我国人口总规模的影响有限[30]，但全面二胎政策带来的人口增长能量是累积的。这种影响可能会持续十年以上。已育一孩的妇女计划生育二胎的时间主要集中在未来4年，其中第二年为峰值[31]。因此，我们推测，全面二胎政策带来的人口变化对义务教育年限向下延长的影响更明显，对义务教育年限向上延长的影响滞后一些。模拟决策系统通过对未来学龄人口规模的预测并结合当前的生育政策，将为义务教育年限延长决策提供一定参考价值。

五、结束语

本文借助计算机模拟技术，采用LESLIE模型预测学龄人口结构变化，根据不同人口年龄段的生育率和生存率对未来人口发展进行推演，预测的准确度相对较高，并得到幼儿园到高中不同阶段的学龄人口结构数据和发展趋势，为基础教育的资源配备和管理决策提供一定参考价值。

根据文本研究的学龄人口趋势，相关教育管理部门可以合理调整撤并学校的进度，使教育资源达到最优化，同时可以合理调整教育经费的投入规模。对于义务教育年限延长决策而言，参考学龄人口预测趋势可以为决策提出新思路，通过分析现阶段九年义务教育的普及程度、效度和教师资源配备程度为是否进行义务教育年限延长提供有力的数据支撑。此外，考虑到LESLIE人口预测规模的假设前提，模拟决策系统预测的人口数据必须结合当前二胎政策对未来的人口结构特别是学龄人口规模带来的影响做具体分析。总之，我国基础教育的学龄人口预测研究对义务教育年限延长决策具有深刻影响，对我国义务教育的管理决策、基本资源配备以及教育经费投入具有一定的指导意义。

[1] 顾小清,林仕丽等.教育数据30年:从CMI到DDDM[J].电化教育研究,2010,(9):55-63.

[2] 吴岩,刘永武等.逐步实施十二年义务教育:新世纪北京教育发展的战略选择[J]. 教育科学研究,2002,(8):5-9.

[3] 蒙秋霞.深圳将延长义务教育年限[J].海南政报,2000,(1):44.

[4] 徐广宇.实施义务教育不可冒进[J].教育发展研究,2002,(6):25-29.

[5] 徐谨严.实施义务教育不可冒进——对延长义务教育年限的几点不同认识[J]. 中国教育学刊,2002,(5):33-35.

[6] 顾小清,黄景碧等.让数据说话: 决策支持系统在教育中的应用[J].开放教育研究,2010,16(5):99-106.

[7] 许邦兴.高校生源缩减的原因、影响与应对策略[J].西北民族大学学报(哲学社会科学版),2013,(5):138-146.

[8] 李渤海.农村基础教育出现的新问题及对策[J].甘肃教育,2010,(13):9.

[9] 颜淑霞,俞玲萍等.生源变化与上海市基础教育的可持续发展[J].上海教育科研,2004,(7):9-13.

[10] 闫建璋.我国延长义务教育年限的合理性研究[D].武汉:华中科技大学,2009.

[11] 肖兴安.延长义务教育年限至12年的可行性研究[J].陕西教育学院学报,2012,(1):10-14

[12] 唐家德.基于MATLAB的非线性曲线拟合[J].计算机与现代化,2008,(6):15-19.

[13] 王可,毛志伋.基于Matlab实现最小二乘曲线拟合[J].北京广播学院学报(自然科学版),2005,(2):52-56.

[14] 罗成汉,刘小山.曲线拟合法的Matlab实现[J].现代电子技术,2003,(20):16-17.

[15] 茆长宝,程琳.两种人口预测模型的精确度比较——以人口年龄移算法和灰色预测模型为例[J].南京人口管理干部学院学报,2009,(1):29-32.

[16] 唐丽芳,贾冬青等.用MATLAB实现灰色预测GM(1,1)模型[J].沧州师范专科学校学报,2008,(2):35-37.

[17] 周瑞平. GM(1,1)模型灰色预测法预测城市人口规模[J].内蒙古师范大学学报(自然科学汉文版),2005,(1):81-83.

[18] 尹春华, 陈雷.基于BP神经网络人口预测模型的研究与应用[J].人口学刊，2005,(2):44-48.

[19] 付艳茹.基于MATLAB曲线拟合的应用研究[J].吉林师范大学学报(自然科学版)，2010,(2):55-58.

[20][24] 付艳茹.基于MATLAB的人口预测研究[D].上海:华东师范大学,2010.

[21][23][27][28] 教育部.国家中长期教育改革和发展规划纲要(2010-2020年) [EB/OL]. http://www.china.com.cn/policy/txt/2010-03/01/content_19492625_3.htm,2015-12-30.

[22] 何卓.对我国农村中小学布局调整的思考[J].教育发展研究,2008,(1):35-39.

[25] 王丽英.义务教育学制年限之争论[J].新西部(理论版),2013,(6):114-115.

[26] 肖兴安.延长义务教育年限至12年的可行性研究[J].陕西教育学院学报,2012,(1): 10-14.

[29] 国家教育督导团.国家教育督导报告2008(摘要)——关注义务教育教师[J].教育发展研究,2009,(1):1-5.

[30] 李博涵.单独二胎政策的出台对我国人口规模及结构的影响研究[J].知识经济,2014, (2):20-21.

[31] 翟振武,张现苓等.立即全面放开二胎政策的人口学后果分析[J].人口研究,2014,(2): 3-17.

责任编辑：李馨 赵云建

Research on Simulation of Schooling Year Extension of Compulsory Education:Perspective of School Age Population Prediction

Xue Yaofeng1, Yang Qiwen2, Gu Xiaoqing1
(1.Department of Educational Information Technology, East China Normal University, Shanghai 200062; 2.Department of Curriculum and Instruction, East China Normal University, Shanghai 200062)

The decision of schooling year extension of compulsory education is closely related to economy, culture and population.Based on the data analysis technology, according to the sixth national census data and the historic population data, we use the LESLIE population model to predict the development trend of the school age population in the future. Through the analysis of features of the school-age population trends of 2016-2025 years, combining with the education decision theory, several countermeasures and suggestions are put forward.

Schooling Year of Compulsory Education; Basic Education; Population Prediction; LESLIE Model

G434

：A

1006—9860(2016)03—0021—06

薛耀锋：博士，副研究员，研究方向为计算机辅助教育、决策支持系统 (yfxue@deit.ecnu.edu.cn)。

杨棋雯：在读硕士，研究方向为教育信息技术(51140105081@ecnu.edu.cn)。

顾小清：博士，教授，研究方向为教育信息化理论与实践、教育培训系统设计开发、远程教育技术、CSCL、学习技术系统用户行为研究、学习技术系统标准研制(xqgu@ses.ecnu.edu.cn)。

2015年12月15日

* 本文得到华东师范大学学校项目“义务教育延长模拟”(项目编号：14000-5154A5-15001_001_002)、上海市科委科技攻关重大项目“上海数字化教育装备工程技术研究中心持续研发项目”(项目编号：13DZ2280300)的支持。

① 顾小清为本文通讯作者。