让学生在数学学习体验中成长

□范玲玲

让学生在数学学习体验中成长

□范玲玲

体验对于学习有着重要的意义，学生只有亲身体验、真心感悟，才能真正将书本中的知识变成自己的能力。因此，在课堂教学中教师应积极创造条件，给学生提供更多的机会去体验，使学生在亲身体验中不断地实现自我超越和自我实现。

数学；学习过程；体验

现代教育理论认为，体验对于学习有着重要的意义，学生只有亲身体验、真心感悟，才能真正将书本中的知识变成自己的能力。在课堂教学中，学生的学习过程是借助于一定的教学情境，在与老师、同伴及教学信息的相互作用中获得基本知识，形成基本技能，感悟基本数学思想方法，积累数学活动经验的。作为课堂教学的组织者、引领者和合作者，我们必须为学生创设生动而有意义的数学活动，让学生亲身体验、真心感悟，形成学力。

一、创设问题情境，在体验中建构知识

现代心理学认为：儿童在无拘无束的活动中，在愉快、和谐、轻松的气氛中能思维活跃、想象丰富、记忆力增强。因此，在教学中，教师可结合教学内容、生活实际与学生求知心理之间所产生的认知冲突，创设有意义的情境，提供给学生体验学习的机会，使学生主动参与学习过程，在体验中建构知识，并形成更为丰富的学习体验。

例如，“圆的认识”教学时，创设 “寻宝物”情境：宝物距离梁妃塔3米处，宝物可能藏在什么地方？如果用红点代表塔，用3厘米长的线段代表宝物与梁妃塔的距离，请在纸上画一画，想一想，如果把你们找到的这些点连起来，会是什么图形？由此引导学生初步感悟圆，再用课件演示，形成圆的表象。就这样，让每一位学生在情境中观察、探索、推理，在这个过程中，学生经历了一维到二维的跨越，清晰认知到圆是由一条曲线围成的图形。

再如，教学 “小数加减法”时，设计如下情境：学校举行了广播操比赛，请看下面的评分表，同学们最想了解什么数学问题？

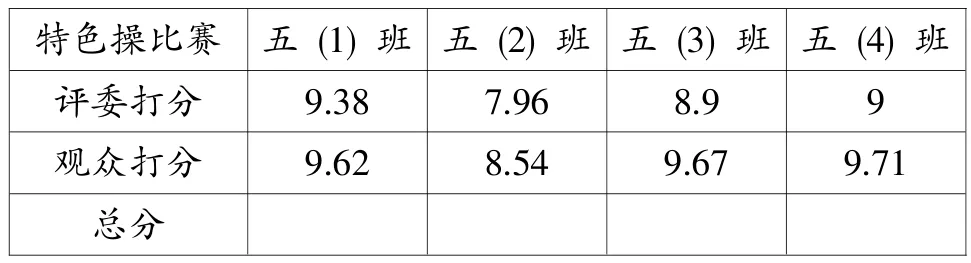
特色操比赛　五 （1）班 五 （2）班 五 （3）班 五 （4）班评委打分　9.38　7.96　8.9　9观众打分　9.62　8.54　9.67　9.71总分

课堂上，学生纷纷提出了自己的问题：我想了解各个班级的总分是多少；我最想了解哪班第一；我最想了解哪班最后；第二名与第三名相差几分；第二名需要再得多少分才能达到第一名；等等。老师借机把学生引入到小数加减法的学习中去。在探究计算方法时，又有学生提问：小数位数不相同怎么对位？要注意什么？整数减小数怎么减？教师引导学生小组合作，讨论小数加减法的对位问题以及进退位问题，在讨论中逐步理清小数加减法与整数加减法的异同点，掌握了计算方法。通过有意义的问题情境，让学生总是处在一种积极的学习状态中：听得仔细、想得认真、做得投入，真正体现了以积极的情感投入、极大地调动思维活动，让学生真正成为学习的主体，促进知识的迁移和思维的提升，让学生在体验中建构知识。

二、构设动手操作，在体验中内化知识

“儿童的智慧在自己的指尖上”。学生通过动手操作活动获取的直接经验和亲身体验，利于促进思维的发展，而思维的发展又有助于动手能力的提高。通过画一画、比一比，摸一摸、算一算等多种活动，帮助学生架起思维和建构的平台，让学生在 “做中想、想中学”，亲历各种有价值的探索活动，在动手中体验，在体验中内化知识。

例如，在 “图形的规律”的教学时，用小棒摆两个这样的三角形需要5根小棒。如图按这样的摆法，11个三角形……需要几根小棒？

笔者先让学生进行猜测，当他们感到无法确定时，就让其边摆边想三角形个数与小棒根数之间的关系。学生们猜出了很多答案，但又不能确定，那该怎么办呢？有学生提出可以边摆边想三角形的个数与根数之间的关系。最后得出了三种方法：3+2×10=23、2×11+1=23、3×11-10=23；90个呢？n个呢？你有什么发现？可用3+2（n-1）、2n+1、3n-（n-1）；因为有了动手操作的过程，学生的活动经验与思维经验得到了有机的结合，对于知识的获取不仅知其然更知其所以然，在体验中内化了知识，而学生已有的数学活动经验也在这类探索活动中，通过自身的强烈感受而充满了活力。

再如，教学 “平行四边形的认识”时，先让学生猜测一下平行四边形有什么特点？再让学生量一量、推一推，分组研究平行四边形有什么特点？把发现的规律写下来，当得出平行四边形的特点后，紧接着让学生先判断下面哪一组小棒可以拼成平行四边形？①6、6、5、4；②3、6、4、3；③7、5、7、5。再让学生动手摆小棒，搞清平行四边形的两组对边互相平行且相等，通过摆小棒，量一量、推一推等活动，加深了学生对平行四边形特点的认识，让每个学生用自己内心的体验和参与去学习数学，亲历知识的形成过程，真正实现了对知识的内化和认同。

三、架设生活实践，在体验中深化知识

数学来源于生活，又服务于生活。在数学学习中，我们要适当引导学生把所学的数学知识和方法应用于生活实际，这样既可以加深对知识的理解，使学生学会从不同角度去分析、概括、运用所学的数学思想方法，使学生在解决生活问题中深化认知。如学生在做简便计算140-99时，易算成140-100-1，于是采用“超市购物的情境”：你共有140元钱，共买了学习用品99元，该怎样付钱？售货员该怎样找钱？你还剩多少钱？学生都明白拿出100元，售货员阿姨找回了1元，还剩41元，这样学生就能搞清楚多减了要加，多加了要减。因此，在教学过程中就要回到生活，将抽象的数学知识融入到生活中去，培养学生运用数学知识的能力。

四、巧设拓展空间，在体验中活用知识

巧设拓展空间，有利于激发学生的学习动机，开启学生的思维潜能。因此，在教学中，我们要引导学生大胆地进行猜测、设想，在验证体验过程中，不断地发现新的问题，分析新的问题，灵活运用所学知识解决新的问题，从而激活学生的思维能力，培养学生的 “四能”，提升学生的学力。

例如，教学 “长方体和正方体表面积”是这样设计的：棱长为1厘米的立方体表面积是多少？将这样的几个立方体摆一排拼成长方体，它们的表面积会发生怎样的变化？请填表格，完成下面的问题。

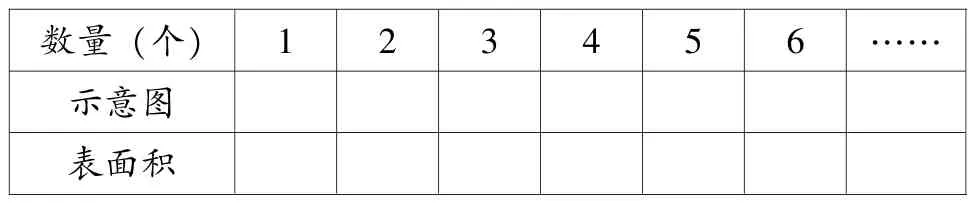
数量（个）　1　2　3　4　5　6　……示意图表面积

观察：用数个相同的小立方体拼成一个长方体，所形成的长方体表面积与原来小立方体表面积之和比较，有什么关系呢，表面积各减少了多少？表面积减少的量有没有规律？如果继续摆下去，100个呢？n个呢？学生一边操作，一边思考，初步感受到这个变化存在着一定的规律，长方体中的接口数比正方体个数少1，隐藏的正方体面的个数是长方体接口数的2倍，隐藏的正方体面的个数是正方体的个数减1的差的2倍。由此，学生经历了数学思考的整个过程。学生在这个解决问题的过程中积极思考、努力探索，利用已有的知识经验寻求解决问题的方法和策略，感悟方法与策略的意义，体验探索过程的乐趣。

再如，“比的意义”练习是这样设计的，根据 “男生人数与女生人数的比是2∶3”，你可以得到哪些相关的信息？该问题促进学生进一步回顾比的意义、沟通比与除法以及比与分数之间的关系，努力根据已知信息寻找相关的信息：男生人数是女生人数的2/3，女生人数是男生人数的3/2，女生人数是总人数的3/5，男生人数是总人数的2/5，男生比女生少1/3，女生比男生多1/2，等等。“男生人数与女生人数的比是2∶3”还可以怎样表示？有的学生说：如果男生是10人，女生就是15人，如果男生20人，女生就是30人，学生通过举例子的方法，也可以通过画一画的方法，只要比的前项和后项同时乘相同的数都可以，为下节课学习比的基本性质做好准备。因此，教师要巧设拓展空间，引导学生自主探究引发新的问题，获得新的结论，从而拓展学生的思维。

总之，在课堂教学中教师应积极创造条件，给学生提供更多机会去体验，使学生不断地实现自我超越和自我实现，在焕发着生命活力的课堂教学中，让学习数学的体验不断成长。

［1］刘家霞.在认知冲突中体验感悟数形结合思想的内涵与价值［J］.教育界，2014，（8）.

［2］李晓.解析小学数学教学中有效开展体验教学［J］.新课程·小学，2013，（4）.

［3］孙丽燕.尊重儿童体验 促进概念学习［J］.小学数学教师，2015，（2）.

［4］李成琼.刍议小学数学体验教学模式的有效开展［J］.科学导报，2013，（6）.

（编辑：杨迪）

G623.5

A

1671-0568（2016）09-0084-02

范玲玲，浙江省天台县赤城街道第二小学教师。