以生为本 展示自我
——创设中学数学高效课堂
□吴韩萍
以生为本 展示自我
——创设中学数学高效课堂
□吴韩萍
建构高效课堂的目的是有针对性地创设开放性课堂,让学生参与课堂学习,为学生提供亲身经历的过程、自我表现的机会和条件,让师生不同的观点和解法都能够得到充分的展现,最大限度地激发学生的创造性思维。
课堂教学;前置作业;小组合作;课堂展示;适时评价
一、抓好课堂教学,调动学习积极性
课堂是学生学习的 “主战场”,也是数学学习的重要环节。因此,教师应把课堂还给学生,让每个学生都有能够展示自我的舞台。抓住课堂教学的根本,把教学内容从大堆的知识点转变为知识的 “灵魂和线段”,创造出尽可能大的空间,迎接学生积极的学习。
例如,教学 “二元一次方程”这节课时,课前给学生留了前置作业:预习教材P80-81,完成以下问题:①写几个你所知道的方程;②写几组满足方程3x+2y=10的x、y的值;③从上述两题中可归纳出什么?课堂上,先给10分钟时间,让学生就前置作业展开小组交流,然后由小组代表展示各组结果。令笔者意外的是,第①题学生展示的方程很多,有2x+3=7,+5=9,x+y=2,3x-y=4,+3=y,x2+ 2y=7等。
师:2 x+3=7是什么方程?
学生齐声回答:一元一次方程。
师:下面呢?
师:二元一次方程应满足哪些条件?
生3:①方程中含有两个未知数;②未知数的次数是一次。
师:有不同意见吗?
生4:他说的不完整,第2点应是含有未知数的项的次数都是一次。
生5:还有,等号两边都是整式。
学生从以前学习的一元一次方程扩展到二元一次方程,并且引出书中未出现的二元二次方程、分式方程等,把二元一次方程的概念叙述得非常到位。学生学习的积极性非常高,气氛很活跃。可见,要改变学生厌学的现状,首先教师应更新教学观念,将教师教转变为学生学。
二、开展小组合作学习,培养综合能力
华南师范大学教授郭思乐提出:教学就是学生在教师的组织引导下的自主学习,生本的课堂区别于考本、本本、师本,是人的发展的课堂。课堂要全面依靠学生,把课堂还给学生,让学生通过自主学习、小组合作交流、小组上台展示、班级交流提升、教师适当点评这些环节培养学生的学习兴趣、学习能力。
例如,在 “二元一次方程组的应用 (1)”这堂课中,笔者进行如下尝试:
前置作业:①找出问题中的已知条件和未知数;②从题中可得到什么等量关系?③怎样设未知数?可以列得什么方程?
案例1:用如图1中的长方形和正方形纸板作侧面和底面,做成如图2的竖式和横式两种无盖纸盒。现在仓库里有1000张正方形纸板和2000张长方形纸板,问两种纸盒各做多少个,恰好将库存纸板用完?

x只竖式纸盒 y只横式纸盒 合计正方形纸板的张数 1011长方形纸板的张数 2024
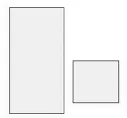
图1

图2
生1:等量关系是竖式纸盒正方形纸板的张数+横式纸盒正方形纸板的张数=1000,竖式纸盒长方形纸板的张数+横式纸盒长方形纸板的张数=2000。
解:设竖式纸盒有x,横式纸盒有y。

由①得x=1000-2y……③
把③代入②中解得y=400
把y=400代入③解得x=200
生2:老师,没告诉我们两种纸盒中有几个长方形,几个正方形。
生1:竖式纸盒中有4个长方形、1个正方形,横式纸盒中有2个正方形、3个长方形。
生3:设未知量中x、y应带单位。
生4:我认为用加减法比较简单。
虽然 “生1”的叙述没一步到位,但通过同学提问、补充等方式,大家共同解决了问题。学生给出的答案不够全面时,教师适时点拨、引导即可。在小组活动中,组内成员会互相帮助,畅所欲言。通过合作交流,学生学会了思考,增加了自信心。在展示过程中,学生暴露出的学习问题,教师应及时、有效地解决。
三、及时鼓励,适时评价,增强学生信心
教师应让每个学生的长处都得到发扬,让每个学生的短处都能转化为长处。课堂上,教师一个小小的鼓励,哪怕是点个头、微微一笑,都可给学生极大的信心。
案例2:下面的计算对吗?如果不对,应怎样改正?①a3·a3=2a3;②a2·a3=a6。
生1:错!正确的是a3·a3=a6。
师:很好!为何结果会得2a3?
生2:把a3·a3看成了a3+a3。
师:很好!还有其他可能吗?
生3:看到了a3·a3,发现a3出现2次,就得出2a3的错误结论。
师:还有其它看法吗?
生4:a3·a3可能会得到a9。
师:怎么得到的?
生4:3×3=9。
师:很好!这种情况也有可能,还应注意什么?
生5:同底数幂相乘,底数不变,指数相加,指数不是相乘。
这位学生弥补了另一个漏洞,教师应及时鼓励学生敢于质疑,大胆思考,大胆发言,增强学生的自信心。
案例3:计算,并用幂的形式表示(-5)2×(-5)3×54的结果。
生1:(-5)2×(-5)3×54=(-5)2+3+4=(-5)9
师:有不同意见的可上来展示。
生2:(-5)2×(-5)3×54=(-5)2+3+4=(-5)9=-59
生3:(-5)2×(-5)3×54=52×-53×54=-52+3+4=-59
生4:(-5)2×(-5)3×54=-(52+53+54)=-52+3+4=-59
生5:(-5)2×(-5)3×54=(-5)2×(-5)3×(-5)4
=(-5)2+3+4=(-5)9=-59
学生陆续上黑板书写时,笔者并没有立即评价,只是微笑地看着学生演示。每个上前展示的学生写完后都看笔者一眼,然后信心十足地回到了座位上。台下的学生因为没有得到教师的反馈,于是继续思考,有的小组还低声讨论,最后学生开始举手,表达各自看法:生1计算过程不完整,结果应是-59;生2底数未转化一致,所以不能用同底数幂乘法法则运算;生3两个运算符号不能连用;学生4粗心错误;生5正确。
生6:还可以把底数都转化为5,(-5)2×(-5)3×54=52×(-53)× 54=-52+3+4=-59。
师:太棒了!表述很完整,感谢这些上来展示的同学,把解题过程中可能出现的问题都展示出来了。
若此时教师迫不及待地予以否定,就会在无形中扑灭学生创造性思维的火花,挫伤学生的积极性。在课堂上,教师的适时评价能为学生创造宽松、和谐、活跃的氛围,让学生静心观察、分析和概括,可使学生在宽松的心理环境中发现错误,愉悦地认识错误,创设析疑的课堂环境。
只要用心去营造 “畅所欲言,各抒己见”的课堂氛围,为学生提供亲身经历的过程、自我表现的机会和条件,让师生不同的观点和解法都得到充分展现,就能最大限度地激发学生的创造性思维,使学生的思维在激烈的碰撞中得到质的升华,达到预期的学习效果。
[1]郭思乐.教育走向生本[M].北京:人民教育出版社,2012.
[2]郭思乐.谛听教育的春天[M].合肥:安徽教育出版社,2008.
[3]陈志强.高中数学教学中如何培养学生的问题意识[J].新课程研究(下旬),2014,(7).
(编辑:易继斌)
G633.6
A
1671-0568(2016)09-0109-02
吴韩萍,浙江省义乌市稠江中学教师。

