周期数对双周期对称结构光子晶体透射谱的调制

唐秀福

(河池学院　物理与机电工程学院， 广西　宜州　546300)



周期数对双周期对称结构光子晶体透射谱的调制

唐秀福

(河池学院物理与机电工程学院， 广西宜州546300)

利用传输矩阵法理论，计算、研究周期数对双周期对称结构一维光子晶体透射谱的影响，结果发现：当光子晶体为单周期对称结构时，随着周期数的增大，透射谱中透射峰的带宽会越来越窄；当光子晶体为双周期对称结构时，随着外层光子晶体周期数的增大，透射谱中的能带逐渐振荡最后分裂成分立的窄透射峰，随着内层光子晶体周期数的增大，透射谱中的分立透射峰向禁带中心靠拢，形成简并的趋势，而且透射峰带宽也会越来越窄。周期数对双周期对称结构一维光子晶体透射特性的调制规律，为光子晶体设计光学滤波、光学开关等新型光学器件提供理论依据。

光子晶体；双周期；周期数；透射谱；调制

0　引言

光子晶体[1-2]诞生半个多世纪以来，一直是研究者们研究的热点，而且在研究和应用上取得了大量成果[3-16]。光子晶体最潜在的应用前景是为新型光通信工具提供材料支撑，很多学者甚至认为光子晶体是以光子替代电子进行信息传输的最佳载体材料。众所周知，光子晶体最突出的光学特性就是能够对光频率进行选择性裁剪，亦即通过合理构造和调整光子晶体的结构或参数，可以选择性地允许某些频率的光通过光子晶体，这种裁剪功能为人为控制和利用光的行为提供了设计和制备依据，同时也体现了光子晶体的广阔应用前景。从结构的对称性角度看，常见的光子晶体结构有非对称结构和对称结构[3-11]，从排列周期结构角度看，又可分为单周期、双周期和多周期结构等。对于单周期结构，排列周期数单一，通过改变排列周期数调节结构的方法也相对较为单一，而对于双周期或多周期结构，由于周期参数多，则通过排列周期数改变光子晶体结构的灵活性也会大为提高。而且，最关键的是，当排列周期数改变时，光子晶体的结构将跟着改变，最终导致其透射特性也跟着改变，即通过调节排列周期数可以调整光子晶体的透射谱特性。目前，关于排列周期数对双周期或多周期对称结构光子晶体透射谱的影响，报道文献还没看到，而本课题不仅是光子晶体理论研究的需要，也是实际设计中遇到且需要解决的问题。

本课题基于这种考虑，在构造单周期对称结构一维光子晶体模型(AB)m(BA)m和双周期对称结构一维光子晶体模型(AB)m(BA)n(AB)n(BA)m的基础上，通过计算机编程计算模拟的方式，仿真出它们的透射能带谱，并进行对比分析。然后重点模拟出排列周期数对双周期对称结构一维光子晶体(AB)m(BA)n(AB)n(BA)m透射谱的影响，最后分析总结出排列周期数影响和调制透射谱的规律，为光子晶体研究和设计提供依据。

1　研究方法和模型

鉴于本课题研究的主要任务是光子晶体的透射能带谱，因此采用的研究理论方法为传输矩阵法，传输矩阵法的要点是分别用单个传输矩阵来描述光在各介质薄膜层中的传输行为，然后再以这些分传输矩阵的乘积得到总矩阵来描述光在整个周期性排列结构中的传播行为，根据这个总传输矩阵就可以计算出光通过光子晶体这个结构整体的反射率、透射率和电场分布等，从而确定光通过光子晶体的传输特性[3-16]。传输矩阵法已经使用得很广泛，而且已经有很多文献作了比较详细的报道，详细可见文献[16]，在此不复述。

构造和研究的对称结构双周期一维光子晶体模型为(AB)m(BA)n(AB)n(BA)m。A、B是周期性排列组成光子晶体结构的基元薄膜介质，本课题计算研究中，它们的取值参数(厚度和折射率)分别为：dA=281 nm，nA=1.38，dB=165 nm，nB=2.35，dC=λ0/nC，nC=1.38。λ0是光子晶体禁带中心频率对应的波长，本模型λ0=2(nAdA+nBdB)=1 551.1 nm。m、n分别为外层与内层光子晶体的排列周期数，计算时为正整数变化。从研究模型可看出，(AB)m(BA)n(AB)n(BA)m其实是由两组(AB)m(BA)n连续排列形成，或是由对称结构的(BA)n(AB)n和(AB)m(BA)m内外嵌套而成。由于光子晶体模型由内外对称结构光子晶体组成，且内外对称结构的光子晶体均有各自独立的排列周期数，组成的总光子晶体结构也是对称的，因此称光子晶体模型为双周期对称结构。

2　研究结果与分析

2.1周期数对单周期对称结构光子晶体透射谱的调制

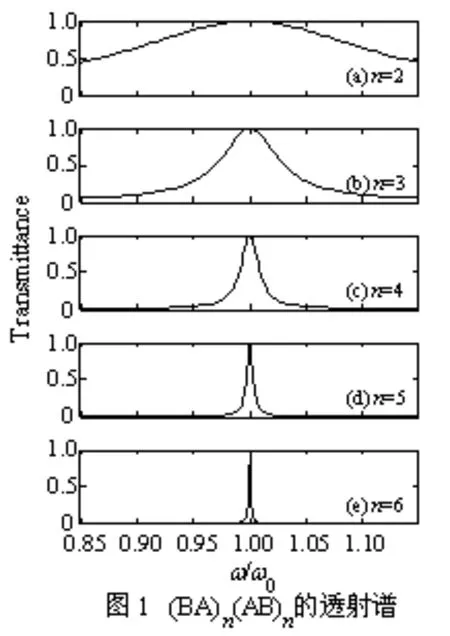
光子晶体(AB)m(BA)n(AB)n(BA)m由(BA)n(AB)n和(AB)m(BA)m内外嵌套而成，两者均为单周期结构对称结构一维光子晶体。那么，周期数对单周期对称结构光子晶体的透射特性有怎样的影响呢？在此，取n=2、3、4、5、6逐渐递增，通过计算模拟，绘制出光子晶体(BA)n(AB)n随着排列周期数n变化的透射谱，如图1所示，图中横坐标以相对频率ω/ω0为单位计量。

从图1可见，当排列周期数n较小时，光子晶体(BA)n(AB)n的禁带中心频率处两侧首先出现很宽的透射带，随着n增大，中心频率处两侧的透射带带宽逐渐变窄形成透射峰，当n=6时，中心频率处仅存在一条很细的窄透射峰。同时，还可以看到，随着n增大，虽然禁带中心频率两侧的透射带逐渐变窄，但无论是最初的透射带，还是最终的窄透射峰，它们的中心一直保持在中心频率1.00ω/ω0处，而且透射带或透射峰的数目也一直保持一条不变，即透射带或透射峰对称分布于中心频率处两侧，如图1(a～e)所示。这种特性符合对称结构光子晶体透射能带谱的特征[3-11]。进一步计算还发现，m对单周期对称结构光子晶体(AB)m(BA)m透射谱的调制规律与(BA)n(AB)n类似，鉴于文章的篇幅，于此不再详细罗列。

因此，单周期对称结构光子晶体的周期数仅能调制透射带或透射峰的带宽，但对透射带或透射峰的数目及其所处的中心位置则不具备调制作用。这种调制机制对设计单通道宽带或窄带滤波器件有一定的理论参考价值。

2.2外层周期数对双周期对称结构光子晶体透射谱的调制

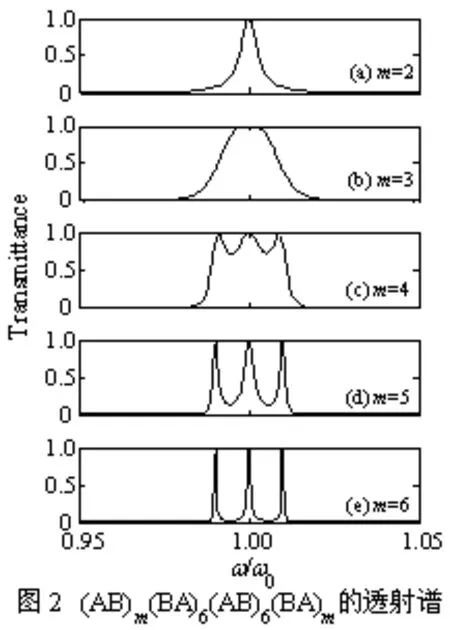
当单周期对称结构光子晶体(BA)n(AB)n和(AB)m(BA)m内外嵌套组合成(AB)m(BA)n(AB)n(BA)m结构时，光子晶体的排列周期数分为内层排列周期数和外层排列周期数，它们对双周期对称结构透射特性的影响是否与单周期一样呢？首先，在其他参数不变的情况下，固定内层光子晶体的排列周期数n=6，取外层光子晶体的排列周期数m=2、3、4、5、6依次递增，计算模拟得光子晶体(AB)m(BA)6(AB)6(BA)m的透射能带谱，如图2所示。

从图2可见，当外层光子晶体的排列周期数m较小时，光子晶体的禁带中出现一条带宽比较窄的透射带，随着m的增大，该透射带逐渐变宽，当m=4时，宽透射带上端开始出现振荡，进而劈裂成3条带宽较宽的透射峰，当m=6时，形成3条窄带透射峰，如图2(a～e)所示。可以推测，随着m继续增大，这3条透射峰会更加精细。形成原因可以分析为，当m较小时，光子晶体主体结构为(BA)6(AB)6，这种镜像对称结构光子晶体，一般在禁带中心频率处出现一条透射峰。随着m的增大，(AB)m(BA)m作用逐步增加，当增大到4时，外层光子晶体与内层光子晶体接触处形成2处缺陷开始体现出来，因而透射带顶端开始振荡劈裂。当m越大，此两处缺陷作用更加明显，最后形成3条窄透射峰。另外，从图2还可以看到，无论是宽的透射带还是窄的3条透射峰，它们均对称分布于中心频率1.00ω/ω0处两侧，这也符合镜像对称结构光子晶体透射谱的显著特征[3-11]。

可见，外层光子晶体的排列周期数不仅可以调制双周期光子晶体透射峰的带宽，而且还可以调制透射峰的条数。这种调制机制对设计多通道宽带或窄滤波器件有积极的参考意义。

2.3内层周期数对双周期对称结构光子晶体透射谱的调制

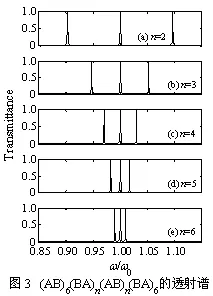
类似地，固定外层光子的排列周期数m=6，取内层光子晶体的排列周期数n=2、3、4、5、6依次递增，可计算模拟出光子晶体(AB)6(BA)n(AB)n(BA)6随n变化的透射谱，如图3所示。

从图3可见，光子晶体(AB)6(BA)n(AB)n(BA)6的禁带中出现了3条窄透射峰，而且这3条透射峰对称分布中心频率1.00ω/ω0处两侧。当n增大时，中心频率处两侧的两条透射峰向中心频率处靠拢，出现三合一的简并趋势，而且透射峰的带宽越来越窄，如图3(a～e)所示。如，从左至右，3条透射峰所处的频率位置，当n=2时，分别处于0.90ω/ω0、1.00ω/ω0、1.10ω/ω0，当n=3时，分别处于0.95ω/ω0、1.00ω/ω0、1.05ω/ω0，当n=4时，分别处于0.97ω/ω0、1.00ω/ω0、1.03ω/ω0，当n=5时，分别处于0.98ω/ω0、1.00ω/ω0、1.02ω/ω0，当n=6时，分别处于0.99ω/ω0、1.00ω/ω0、1.01ω/ω0。可以推测，当n增大到一定数值时，3条透射峰将出现三合一的简并现象。以左侧透射峰为研究对象，并以透射峰的半高全宽计量其带宽[5-7,12-13]，则通过计算可得，当n=2时，透射峰带宽为Δω=11.4×10-4ω/ω0，当n=3时，中心透射峰带宽为Δω=6.9×10-4ω/ω0，当n=4时，中心透射峰带宽为Δω=5.9×10-4ω/ω0，当n=5时，中心透射峰带宽为Δω=5.6×10-4ω/ω0，当n=6时，中心透射峰带宽为Δω=5.4×10-4ω/ω0。

可见，内层光子晶体的排列周期数不仅可以调制双周期光子晶体透射峰的带宽，而且还可以调制透射峰所处的频率位置。这种调制机制对设计多通道窄滤波、光学开关等器件有积极的参考价值。

3　结论

在合理构造双周期对称结构一维光子晶体的基础上，通过传输矩阵法，利用科学计算软件编程计算、仿真，研究内外层光子晶体排列周期数对光子晶体透射特性的调制规律，结论如下。

(1)周期数仅能调制单周期对称结构光子晶体透射带或透射峰的带宽，不能调制透射带或透射峰的数目或所处的中心位置。

(2)外层光子晶体的排列周期数可调制双周期光子晶体透射峰的带宽和透射峰的条数。

(3)内层光子晶体的排列周期数可调制双周期光子晶体透射峰的带宽和透射峰所处的频率位置。

所以，相比单周期对称结构光子晶体，周期数对双周期对称结构光子晶体透射特性的调制更加灵活有效。周期数对双周期对称结构一维光子晶体透射特性的这种调制机制，为光子晶体设计新型光学滤波器件、光开关等具有积极的指导价值。

[1] Yablonovitch E. Inhibited spontaneous emission in solid-state physics and electronics[J]. Phys.Rev.Lett.,1987,58(20): 2059-2061.

[2] John S. Strong localization of photons in certain disordered dielectric superlattices[J]. Phys. Rev.Lett.,1987,58(23): 2486-2489.

[3] 苏安,高英俊.双重势垒一维光子晶体量子阱的光传输特性研究[J].物理学报,2012,61(23):234208.

[4] 苏安,高英俊,蒙成举.双重势垒一维光子晶体量子阱内部局域电场分布[J].光子学报,2014,43(2):0216002.

[5] 苏安,蒙成举,高英俊.激活性杂质对光子晶体量子阱滤波器特性的调制[J].中国激光,2014,41(3):0306001.

[6] 苏安,蒙成举,高英俊.实现高品质滤波功能的一维光子晶体量子阱滤波器[J].中国激光,2013,40(10):1006001.

[7] 苏安,蒙成举,高英俊.结构周期数对光子晶体量子阱透射品质影响的研究[J].激光与光电子学进展,2013,50(1):012302.

[8] 苏安,蒙成举,高英俊,等.两端对称光子晶体透射谱的影响[J].激光与红外,2014,44 (11):1253-1257.

[9] 潘继环,苏安,蒙成举,等.垒层周期不对称度对光量子阱透射谱的影响[J].激光与光电子学报,2014,51(1):012701.

[10]苏安,蒙成举,潘继环,等.周期不对称度对光子晶体透射谱特性的影响研究[J].量子光学学报,2014,14(2):154-158.

[11]苏安,陆华,黄星寿.缺陷光学厚度对对称结构一维光子晶体透射谱的影响[J].河池学院学报,2011,31(2):17-21.

[12]苏安,李忠海,莫传文,等.光子晶体滤波器的滤波品质调制因素研究[J].河池学院学报,2014,34(5):78-82.

[13]潘继环,李志海,黄金玉. 介质光学厚度对双负材料光子晶体透射峰带宽的调制[J].河池学院学报,2015,35(2):30-34.

[14]潘继环,苏安,唐秀福,等.缺陷奇偶性对光子晶体光传输特性的影响[J].激光与红外,2015,45(6) :705-709.

[15]韦吉爵,李忠海,莫传文,等. 两种因素对光子晶体缺陷模的影响[J].河池学院学报,2015,35(2):40-44.

[16]唐秀福.光子晶体研究方法对比与实例分析[J] .河池学院学报,2015,43(2):45-49.

[Abstract]The transmission spectrum of the double periodic symmetric structures is studied by using the transfer matrix method. The results show that: In the single periodic symmetric structure photonic crystal, when the period number increases the bandwidth of the transmission peak becomes narrower. In the double periodic symmetric structure photonic crystal, when the period number of external photonic crystal increases, energy band of the transmission spectrum gradually oscillates and finally fractures into separated narrow transmission peaks; when the period number of internal photonic crystal increases, separated transmission peaks of the transmission spectrum will draw close to the forbidden band center forming a degenerate tendency, and the bandwidth of the transmission peak will become narrower. Modulation of double periodic symmetric structure photonic crystal by period number will provide theoretical foundation for the design of new photonic crystal optical devices such as optical filter, optical switch and so on.

[Key words]photonic crystal; double period; period number; transmission spectrum; modulation

[责任编辑刘景平]

Modulation of Transmission Spectrum on the Double Periodic Symmetric Structure Photonic Crystal by Period Number

TANG Xiu-fu

(School of Physics and Mechanical & Electronic Engineering, Hechi University,Yizhou, Guangxi 546300, China)

O431

A

1672-9021(2016)02-0048-05

唐秀福(1985-)，男(壮族)，广西都安人，河池学院物理与机电工程学院讲师，主要研究方向：光子晶体理论和特性。

广西高校科学技术研究基金资助项目(KY2015YB258，KY2016LX287)；2015年国家级、广西区级大学生创新创业训练计划项目(201510605013，201510605040，201510605061)；河池学院校级青年科研基金资助课题(XJ2015QN006)。

2015-10-25