电网工程建设项目中的资源均衡优化问题研究

李阿勇

（北京科技大学 东凌经济管理学院，北京 100083）

电网工程建设项目中的资源均衡优化问题研究

李阿勇

（北京科技大学 东凌经济管理学院，北京 100083）

摘要：文章针对电网工程建设项目计划制定和控制问题，讨论了为求完成计划的最短工期问题和资源均衡消耗问题。对于这两类问题，文章基于传统PERT网络计划，给出了主导线路概念和关键度的概念，并结合实例确定了关键线路的方法，同时对施工总进度及进行完工概率等问题进行分析，并设计了相应的算法过程，提出一种施工资源均衡优化的细菌觅食算法。实例模拟计算表明，利用此算法可求得工期更短、均衡性更优化的施工过程。

关键词：项目需求计划；电网工程项目；PERT；细菌觅食算法

［DOI］10.3969/j.issn.1007-5097.2016.08.026

一、引　言

随着我国电网建设规模不断扩大，为了实现电力传输安全、方便、快捷的目标，电网工程建设面临着多方挑战。相关文献分析表明，电网工程建设过程中物流管理成本占到整个工程总成本的60%以上。对项目开发过程而言，物料需求决定了采购过程的实施，而项目进度计划为物料需求计划的制定奠定了基础，项目进度计划制定的可行性与有效性问题是电网工程建设项目现场物流管理理论研究的热点。由于电网工程建设项目施工系统中各时段对资源的需求量相差很大，所以各组成工序的关系错综复杂。如果不优化施工系统资源计划，在施工过程中则很容易产生抢工或窝工事件。

Clough和Sears对其进行了定义：“为了完成既定目标而制定的可操作的付诸实践的行动方案”［1］。而施工进度计划首先确定了各个施工项目主要工程的工种；其次明确了施工计划及开竣工日期；最终确定施工现场所需要的劳动力、材料和施工机具等。所以，施工进度计划的编制以及准确性对于工程建设项目是否能按期交付，能否充分发挥其投资效益具有重要的作用。正确的施工进度技术是降低工程成本的保证。对于项目计划资源优化问题可以根据优化具体目标的不同分为两类：第一类以最短完成计划的工期为目标，第二类以资源均衡消耗为目标。这两类优化问题目标不同，因此建模过程也有所区别。

二、基于改进PERT的施工进度计划分析

施工进度安排基于已知条件，在合理工期限制内安排与设计工程施工分期和施工程序方案，从而保证各个施工环节在时间安排上相互协调。当制定施工进度计划时，要考虑它与施工组织设计的其他方面、施工的方法以及技术供应等的密切联系，还要分析清楚他们之间的制约关系。施工进度计划的制定属于系统工程问题，所以可以采用系统分析方法来解决。

在系统分析中常用网络计划技术将工程施工过程作为一个整体来分析。通过网络图的方式分析预定计划任务各个环节之间的相互关系。通过计算时间参数，分析寻找关键路径；通过计算时差改进实施方案，从而达到缩短工期、降低成本消耗、节省劳力和提高效率的目的，优化成本、工期和资源［2］。

在工程建设项目的施工进度计划中，施工活动的逻辑关系通常是已知的，并且是不变的，因受到自然条件限制以及实施单位的操作水平和组织管理方面的影响，施工活动的工作时间无法确定。因此，引入计划评审技术法（PERT）［3］。同时，PERT方法存在一定的局限性：

（1）其假设所有活动周期均服从多参数分布，活动周期的均值为 Di=（a+4m+b）/6，误差较大；

（2）工程周期由各项活动周期均值相加得到。在计算中，将均值之和中最长路线上的周期定义为工程周期，导致计算结果比按随机活动周期之和计算时的均值短；

（3）PERT方法认为网络计划图中只有一条关键路线，而在实际项目计划过程中，尽管其他线路并不是主关键线路，但这些线路施工敏感性较强，一旦工程出现延误就会使得这些线路提升为关键线路，而这点在PERT方法中无法得到体现。

利用PERT理论研究工程建设项目中会遇到不确定性情况。本文重点研究不确定性环境下项目工期的变化并对其进行建模［4-5］。

（一）工程工序时间参数计算

关键线路法使用之初要确定项目各工序的逻辑关系，即假设各工序的逻辑关系是确定的，并且用节点最早开始时间、节点最迟开始时间和节点时差的概念描述每项工作的时间，并利用这些参数计算项目工作的工期及时差。在关键线路法的描述过程中，最核心的概念是工序最早时间和工序最迟时间。最早开始时间是假设前一工序进行完毕，下一工序立即开始的时间，最迟开始时间是为了保证后续工期的进行，当前工序必须开始的时间［6］。

假设各分工程施工计划是确定的，估算得到的每项确定的工作时间参数、工期和时差。

在进行工程工序时间参数计算之前，先了解相关参数：

（1）节点最早时间ET。网络计划的开始节点表示，为方便计算，令ET1=0，其他节点的最早时间为：

式中ETj为 j节点的最早时间，ETi为i节点的最早时间，Di-j为工作i-j的持续时间。

（2）节点最迟时间LT。项目时间界限指该节点所有前项工作最迟必须结束的时刻。

节点的最迟时间：

式中，LTj为 j节点的最迟时间，LTi为i节点的最早时间，Di-j为工作i-j的持续时间。

（3）节点时差：STi=LTi-ETi。

工序时间参数：工序最早开始时间ES、最早完成时间EF、工序最迟开始时间LS、最迟完成时间LF，因此得到公式：

工序时差的概念是指工序在一定条件下的机动时间范围，可以分为总时差与自由时差。工序的总时差是指在不影响工期和有关时限的前提下，一项工序可以利用的机动时间。计算i-j工序的总时差：

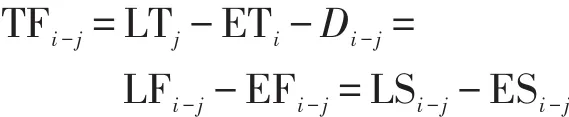
（4）工序的自由时差：计算i-j工序的自由时差FFi-j如下：

（5）PERT就其本质来说是一种随机网络技术，通过多种随机因素构建随机网络用以反映工程工序相关逻辑和计划关系。在实际工作中，工程计划实施情况所需的时间并不是一成不变的，而是会依据资源可用性或其他条件等随机变化，例如对基建项目而言，其工期会受气候变化影响而发生变化。正是由于工序实施情况的随机性以及互动实施时间的估计过程受到很多随机误差的如工作抽样误差的影响，因此活动时间是随机变量而不是固定的。

（二）PERT方法在使用中需要对工程项目及相关工序进行假定

（1）PETR方法假设项目分解的工序数量有限，只有在有限的工序数量下才能构造随机网络。同时，为了保证项目随机性互不影响，或者说项目随机情况不会受到交叉影响，还要求工序之间是完全相互独立的，各个工序有明显的边界。

（2）除了工序之间的独立性，还要求工序持续时间也是相互独立的，并且每项工序持续时间具有明确的概率分布和相应的统计特征，同时为了建模需要，通常假设各工序的周期服从正态分布，以便于随机网络构建过程中对每项工序进行识别。

（3）为了保证中心极限定理能够应用于项目关键路径识别过程中，PERT方法要求关键线路上的活动应该足够多。

（4）为了保证求解过程的稳定性，PERT方法假定对于每个项目而言有且只有一个关键线路。

在非确定型网络计划中，由于随机因素影响，无法确定固定的数值，需要对工作持续时间进行估计，常用的方法是：①利用工作的最短估计时间；②最长估计时间；③最可能估计时间。通过这三个时间估计工作的期望持续时间，而在这三个时间中工作的最可能估计时间的可能性最大，因此在对工作的期望持续时间进行估计时，工作的最可能估计时间占比最大。具体分配比例一般为1∶1∶4，工作的持续时间期望为：

PERT考虑了建设项目施工延续时间的随机不确定因素，然而只适用于延续时间服从于正态分布，但是计划实施的可靠度较低。在实际工程中，建设项目工程进度计划的制定通常根据建设项目的工程量、资源配备和定额估测施工工期，然后再根据施工合同等限制条件确定该工作的开始和结束时间。但是，因为需要事先估算，可能存在服从三角分布或β分布不确定估计量。

（三）关键线路分析

本文通过运用主导线路确定仿真关键线路的方法，对PERT网络展开进一步研究［7］。

节点 j（1＜j≤n）存在于PERT网络中，汇入 j节点共有k条路线ri（i=1，2，…，k），从节点1到节点j线路rj的持续时间为Ti，Ti=∑tij，节点j的规定完工时间为Tf，假设线路rc对应的Tc满足公式条件，则线路rc为主导线路。

（1）对于终节点n，确定汇入的主导线路；

（2）确定沿该主导线路相连的前一节点；

（3）在这节点上找到其主导线路依次确定的开始节点；

（4）最终将所找到节点的主导线路首尾相连即得到关键线路。

所以，线路rc为主导线路，关键度最大的线路为主导线路。

从PERT网络的终节点n沿其主导线路逆着箭线方向，可以找到前节点j（j＜n）；进而从节点 j开始沿其主导线路逆着箭线方向，可以找到节点j的上一节点；同样的，按照以上方法找到关键线路，其流程如图1所示。

图1　关键路径仿真分析流程

其中，Xmin为n次仿真中工期的最小值；Xmax为n次仿真中最大值；m为组数。

（2）分组。令 X1=Xmin+Xg，X2=X1+Xg，…，Xm-1=Xm-2+Xg，则施工工期 T的分组结果为：（-∞，X1），［X1，X2），…，［Xm-1，+∞）。

（3）绘制施工工期的频数分布以及频率直方图。

（4）通过累积曲线可以查到某个施工工期X′的完工概率。

（四）实例分析

某电网工程变电站项目为110/10千伏两级电压地区负荷变电站。主要建（构）筑物有主控室包括10kV开关室、主变间、室外散热器间、GIS间等设备房间）以及事故储油池，变电站主控楼总建筑面积2 457m2。

本项目共包括85个节点，110多个活动。为了进一步研究，本文简化了施工进度网络图但保持了该建设项目的关键路径，项目的施工进度计划见表1所列。

由于受到施工条件限制，其简化步骤如下：（1）设定分组的组距Xg：

表1　项目施工进度计划

本文采用Matlab R2013a作为随机模拟工具，首先建立该建设项目施工系统蒙特卡洛模拟模型，通过仿真软件进行1 000次仿真，最小值为783天，最大值为812天，方差为5.9，均值为797天，均方差为2.429。施工工期的分组组距取为5天，相应的建设项目工期为797天，工期保证率达到59%；当对应工期为802天时，工期保证率可提高到89%左右。关键路线的组成工序为：1→2→3→4→6→12→23→48→55→79→84→85。多次仿真运行得到的关键路线结果比较稳定。

三、基于细菌觅食算法的施工资源优化方法

项目计划安排通常是以工期最短为目标而进行，但有些时候由于工程资源限制以及施工强度均衡考虑，项目计划安排还应该在既定施工期限内达到资源均衡化。由于资源均衡本身概念较为抽象，因此需要给出描述资源均衡的指标。通常而言，评判资源均衡情况其实质就是评判资源偏离程度，统计上对于偏离程度的度量指标通常包括方差、离差、极差等概念，因此对于资源均衡程度的度量也用这些指标来描述［8］，具体指标定义及含义如下：

（1）不均衡系数：

其中，Rmax为施工工期内资源强度的最大值；Rm为施工工期内资源强度的平均值。

（2）方差：

其中，T为施工工期；R（t）为时刻t的资源强度值。

（3）最大绝对离差：

其中，R（t）为时刻t的资源强度值。

（4）极差值：

其中，Rmax为资源强度的最大值；Rmin为资源强度的最小值。

在得到均衡程度的度量指标后就可以对项目计划资源均衡情况进行评判，对于均衡情况比较差的项目计划，需要对其进行调整。传统的调整方法主要有最小方差法和削峰填谷法。这两种方法是传统的手工操作方法，使用起来较为简便，只需结合具体计算出的均衡指标手动对项目计划资源情况进行调整，因此在资源不均衡程度较低时使用具有较好的效果。但当资源均衡程度较差，其资源量和工程涉及过程较多时，这两种方法使用起来就不太方便。本文在此基础上利用启发式算法中的细菌觅食算法构建了第三种资源均衡算法，同时考虑电网工程建设项目过程中日历使用情况，给出了混合细菌觅食算法。

（一）施工资源均衡优化的启发式算法

施工资源均衡优化的传统算法主要有两种：最小方差法和削峰填谷法，都是解决资源均衡问题的手工调整方法，这两种方法虽然在很多情况下可求得可靠的可行解，但是由于上述两种方法过度依赖需解决问题的本身，当问题规模较大或者导致资源强度发生变化的随机因素较多时非常容易导致求得局部最优解［9］。本文采用细菌觅食算法，它具有良好的群搜索能力及并行计算能力，在处理这种带有约束条件的优化问题时具有非常好的处理效果。

Passino通过模拟大肠杆菌觅食过程提出了细菌觅食优化算法（Bacteria Foraging Optimization Algorithm，BFOA）。细菌觅食算法所遵循的生物学原理是模拟人类消化系统内大肠杆菌或粘细菌在觅食过中，一边感应自身周围的化学物质浓度一边做出远离或趋向该种物质的智能行为，遵循了最优觅食理论。Berg等人对细菌觅食算法的收敛性进行了证明，给出了细菌觅食算法的理论基础。细菌觅食算法是一种基于群体的搜索技术，其最大的特点就是有较强的全局搜索能力以及对约束条件的灵活处理方式，故BFO搜索性能优于遗传算法。

细菌觅食算法为从本质上解决“有限工期约束条件下的项目计划资源强度均衡优化问题”提供了理论依据。细菌觅食算法本身对于问题要求较少，同时具有较强的局部和全局搜索能力，算法稳定性也较高。

考虑到无论是最小方差法还是削峰填谷法所使用的均衡指标的单一性，本文在引入细菌觅食算法求解项目计划资源强度均衡问题时同时考虑4种均衡性指标：不均衡系数、方差、最大绝对离差和极差。均衡的目标是使得这四种指标达到最优，但同时要考虑项目计划对于实施时间及总资源强度的要求。另外，对于资源均衡优化来说，目前的优化模型只是从资源强度自身出发，而在实际管理过程中，使用资源日历来协助项目管理人员分配资源，资源平衡应该是事前诸葛亮，以整理工程资源本身为基础进行事前平衡［10］。

符号说明：

n：工序的数量；

T：优化后的工程施工工期；

Qm：资源每天平均需用量；

T（i）：i工序的持续时间；

N：工序的总数；

Si：工序i的紧前工序集合；

m：不同资源类型的数量；

j：i工序的紧后工序；

Ati：ti时刻进行的工序集合；

bk：资源k的总量；

rik：工序i需要资源k的数量；

R（t）：t时刻的项目计划资源强度值；

Qt：第t天的资源需用量；

Qmax：最高峰日期的每天资源总需用量；

Ri（t）：i工序t时刻的资源强度值；

Rm：工程的平均资源强度值；

dj：工序 j的持续时间；

ti：工序i的开始时间；

Ts（i）：i工序实际开工时间；

Tl（i）：i工序的最迟开工时间；

Te（i）：i工序的最早可能开工时间。

建立优化模型如下：

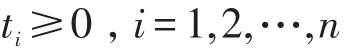
结合细菌觅食算法计算过程如下：

（1）编码方式。本文采用顺序编码的方式对模型进行编码。具体编码方式如下：假设项目的资源强度为qi，则初始编码方案为：q1，q2，…，qn，它代表了资源强度值，每组编码方案代表单个细菌，单个细菌的长度为t。单个细菌记为：

（2）适应度函数确定。 f（vk）是目标值，fmax和 fmin分别是当前种群的最大目标值和最小目标值，vk是当前种群的第k个细菌个体，g（vk）是适应值函数［11］。转换方法如下：

（二）实例分析

某电网工程变电站项目为110/10千伏两级电压地区负荷变电站。计划整个施工周期为26个月，初始的工期内资源强度分布情况如图2所示。

图2　初始的工期内资源强度分布情况

其中横坐标为施工工期，纵坐标为施工资源强度。

首先采用传统的最小方差法和削峰填谷法对项目计划施工资源强度进行优化，优化结果分布见图3、图4所示。

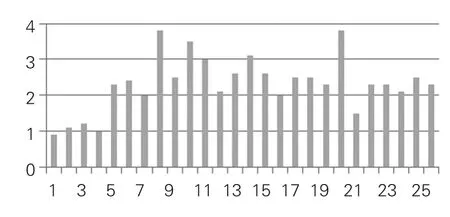
图3　最小方差法优化的施工资源强度分布

图4　削峰填谷法优化的施工资源强度分布

细菌觅食算法参数设置分别为：种群设置为100，复制次数为10，趋向性参数为60，游动参数设为0.5，迁徙次数为20次，迁徙概率设为0.15，总迭代次数约为5 500次。采用混合细菌觅食优化算法计算结果如图5所示。

图5　细菌觅食算法优化后的施工资源强度分布

最大资源强度及资源强度方差对比见表2所列，由此可以得出基于改进的细菌觅食算法得出的施工系统仿真资源均衡优化结果比传统方法（最小方差法、削峰填谷法）所得到的优化结果更接近最优解。

表2　最大资源强度及资源强度方差对比

四、结　论

对项目开发过程而言，物料需求决定了采购过程的实施，项目计划是否能够有效实施是电网工程建设项目现场物流管理理论框架中的关键问题之一。针对电网工程建设项目计划制定和控制问题，本文讨论了在有资源限制情况，为求完成计划的最短工期的资源优化问题。对于这类问题，本文在基于传统PERT网络计划的基础上，最后通过实例验证了了确定关键线路的方法，同时对施工总进度及进行完工概率以及关键线路转移问题都进行了分析［12］。实例模拟计算表明，利用细菌觅食算法可求得均衡性更优化的施工过程。

参考文献：

［1］Meng X，Sun M，Jones M.Maturity Model for Supply Chain Relationships in Construction［J］.Journal of Management in Engineering，2011，27（2）：97-105.

［2］马国丰，屠梅曾，史占中，等.基于关键链技术的项目进度管理系统设计与实现［J］.上海交通大学学报，2004（3）：377-381.

［3］刘颖.大物流工程项目类制造系统及其资源优化配置技术的研究［D］.重庆：重庆大学，2001.

［4］Freeland J R，Moore J H.Implications of Resource Directive Allocation Models for Organizational Design［J］.Management Science，1977，23（10）：1050-1059.

［5］Leu S，Chen A，Yang C.A GA-based fuzzy optimal model for construction time-cost trade-off［J］.International Journal of Project Management，2001，19（1）：47-58.

［6］Thomas H R，Sanvido V E，Sanders S R.Impact of Material Management on Productivity—A Case Study［J］.Journal of Construction Engineering and Management，1989，115（3）：370-384.

［7］李良宝.建设项目施工进度计划仿真研究［D］.哈尔滨：哈尔滨工业大学，2007.

［8］李星梅，张倩，乞建勋，等.对具有时间转换约束网络模型的特性研究［J］.系统工程学报，2013，28（3）：394-402.

［9］王靖.SX电信渠道协同项目管理分析［D］.西安：陕西师范大学，2013.

［10］李海涛.基于遗传算法的工程项目多资源均衡优化研究［D］.大连：大连理工大学，2012.

［11］王卓甫.工程进度风险计算研究［D］.南京：河海大学，2002.

［12］莫俊文.工程进度网络中工时的相依度研究［D］.天津：天津大学，2010.

［责任编辑：欧世平］

中图分类号：F273；F275.5

文献标志码：A

文章编号：1007-5097（2016）08-0173-06

收稿日期：2016-03-01

作者简介：李阿勇（1976-），男，北京人，高级工程师，硕士，研究方向：电网工程技术经济及管理。

Research on Resource Leveling Optimization Problem in Power Grid Project Construction

LI A-yong
（Dongling School of Economics and Management，University of Science&Technology Beijing，Beijing 100083，China）

Abstract：In view of the development and control of power grid project planning，this paper discussed the problem of the shortest time limit for the completion of the project and the balance of resources consumption in the case of resource constraints. For these two types of problems，the paper gave the concept of the leading line and the key degree based on the traditional PERT network plan.And it gave an example to the method to determine the critical path.Meanwhile，it analyzed the general construction and completion probability problems，designed the corresponding algorithm process，and put forward a construction of resource optimization and bacterial foraging algorithm.The simulation calculation showed that the algorithm can obtain time shorter and more balanced optimization of construction process.

Keywords：project requirement planning；power grid project；PERT；bacterial foraging algorithm