天然气市场不同预期规则下的三寡头博弈模型研究

杨　俊，张亚军，张小漫

（重庆大学 经济与工商管理学院，重庆 400044）

天然气市场不同预期规则下的三寡头博弈模型研究

杨俊，张亚军，张小漫

（重庆大学 经济与工商管理学院，重庆 400044）

摘要：文章针对三寡头垄断的天然气上游（供气）市场，基于不同预期规则建立了三寡头动态博弈模型，运用混沌经济学理论求解系统均衡点并进行稳定性分析；最后利用数值模拟研究了主要参数发生变化时系统复杂的动力学行为。结果表明：不同预期规则下的三寡头博弈模型具有非常复杂的动力学特性；自适应企业对市场具有稳定效应，而有限理性企业过快的产量调整速率会导致市场进入混沌状态。

关键词：天然气；博弈模型；预期；混沌

［DOI］10.3969/j.issn.1007-5097.2016.08.002

一、引　言

改革开放30多年来，伴随着我国经济快速发展的同时也导致了资源的大量消耗。由于我国的煤矿资源丰富以及开采、存储和运输成本低，使得在我国一次能源消费中，煤炭一直占有主要地位，2014年一次能源消费中煤炭占比为66%，而这一比例远远高于世界平均水平30%，近些年来由煤炭等化石燃料大量消耗所导致的雾霾等生态环境问题日益凸显，环境治理刻不容缓。在此背景下，党的十八大提出了“坚持节约资源和保护环境”的基本国策，要加快能源向清洁化方向发展。而天然气作为一种优质、高效、清洁的能源自然成为当下能源结构调整破解经济发展与环境污染矛盾最有效的方式。

随着工业化和城镇化的加快，近些年我国天然气产业步入了快速发展的轨道，消费模式由“供应驱动消费”逐步向“需求拉动消费”转变。从表1可知，2014年我国天然气生产量和消费量分别达到1 345亿立方米和1 855亿立方米，较2013年同比增长7.7% 和10.3%，天然气在我国一次能源消费的比重增长到5.7%（但远低于世界平均水平23.7%和亚太地区的11.2%）。根据“能源发展战略行动计划2014-2020”设定的目标，到2020年，我国天然气在一次能源消费中的比重将提高到10%以上。虽然天然气生产量和消费量都呈现快速增长的态势，但是产量的增速跟不上消费量的增速，例如，2005年、2006年、2010年、2012年以及2013年国内都出现了大面积“气荒”，这些充分凸显出目前我国天然气供需的矛盾；同时也导致我国天然气缺口逐年增大，对外依存度不断提高，截至2014年底我国天然气对外依存度达到30.2%，预计到2020将达到50%，这势必会威胁到我国的能源安全。因此，保障我国天然气的稳定供应、确保能源安全将是一个非常重要而又亟须解决的问题。要保障天然气持续稳定的供应无非有如下两个方面的途径：①从国外进口，包括进口天然气和进口LNG。目前中国已经建成了四大天然气进口通道，包括中亚管道天然气、中缅管道天然气、中俄管道天然气以及沿海进口液化天然气。进口天然气虽然在短期内能够缓解国内经济增长对天然气的需求，但进口天然气受地缘政治、地区稳定、国际经济形势等情况影响较大，从长远来看并不利于国内能源安全。②国内开采。目前我国已探明的天然气储量比较丰富，勘探开采潜力巨大，仅2014年全国天然气、煤层气及页岩气等能源类气体新增探明地质储量总量达11 107.15亿立方米，创历史最高水平，呈快速增长趋势。显然，大力勘探和开采天然气将是满足我国天然气需求和保障国家能源安全最为重要和有效的途径。因此，通过分析我国天然气市场结构，研究天然气企业的竞争机制，以求提出一些能够促进我国天然气稳定供应的建议和举措，具有较强的现实意义。

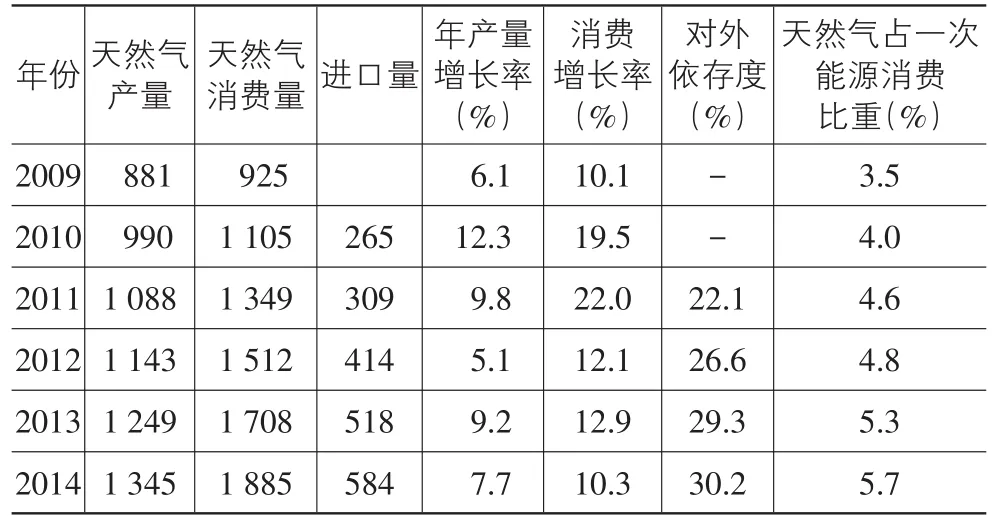
表1　2009-2014年我国天然气生产、消费等情况亿　立方米

和传统的自然垄断行业一样，天然气行业沉淀成本大，其规模经济性和范围经济性较强，而且利润不宜过高，使得我国的天然气上游（供气）市场处于三寡头（中石油、中石化、中海油）垄断的局面［1］。不同的市场结构会导致企业采取不同的竞争行为，必然也会产生不同的市场效果；而三寡头垄断市场在我国是非常普遍的，因此研究三寡头的市场竞争及博弈机制无疑具有较强的现实意义。目前大多数学者对三寡头的研究主要是基于静态的、完全信息和单一策略前提下进行的，然而完全信息假设在现实中必然不会存在，因此它们的决策是居于有限理性进行的；同时由于受制于管理层对市场形势的判断能力、企业的生产规模和信息是否充分对称等条件，企业往往会有不同的预期，因此寡头垄断企业主动参与市场，制定优化可行的策略，实现自身利润最大化是一个非常复杂的过程［2］。近年来，随着非线性科学的发展，尤其是其与经济学的结合所产生的混沌经济学理论不断成熟，使得学者能够更加深入和贴近现实去研究寡头垄断市场。

Agiza等（2010）否定古诺模型中的完全信息假设条件，引入有限理性预期，构建了双寡头动态博弈模型并研究了其具有的动力学特性［3］。Bischi等（2001）将自适应预期引入双寡头模型，分析了双寡头产量博弈的动力学特性［4］。Elsadany（2002）研究了信息不对称和不同预期对厂商决策行为的影响，并求解了模型的均衡解［5］。张骥骧（2008）等基于不同预期规则建立了双寡头模型，研究了分别采用静态预期与有限理性预期的寡头厂商之间的竞争决策问题［6］。

吉伟卓、马海军（2008）在假设企业具有非线性需求及成本函数的基础上研究了三寡头电力市场博弈模型，探究了在初始产量确定与不确定两种情况下电力生产商的最佳产量决策［7］。Chen、Ma（2009）在中国移动通信市场上基于伯川德模型构建了三寡头博弈模型，研究结论表明移动运营商之间的价格调整可能会引起整个通信市场进入无序竞争状态［8］。Ma、Ji（2009）在电力市场上构建了三寡头博弈模型，主要研究了过网费对三寡头竞争行为的影响，结果表明过较高的过网费会提升企业生产成本，企业往往会通过提高电价的方式来转移成本，减少了消费者剩余［9］。

本文假设企业间采取产量竞争策略并结合有限理性及混沌经济学相关研究成果，建立基于不同预期决策规则的天然气市场三寡头动态博弈模型；通过严格的数理推理和数值模拟，分析了天然气市场三寡头在不同预期情形下，为实现利润最大化而采取决策过程中表现出的复杂动力学特性，以期能为我国天然气市场上的企业提供些许产量决策依据。

二、天然气市场三寡头博弈模型的建立

假设天然气市场的寡头企业之间采取产量博弈，且每个企业所生产的天然气是同质的。以?表示第i（i=1，2，3）个天然气企业在t时期的产量，则t期市场的总产量为：

假定三寡头面临着共同的线性逆需求函数：

同时各企业成本函数为：

由式（1）、（2）、（3）可得第i个天然气企业在第t期的利润函数为：

通过求解各企业的最优反应函数可得到纳什均衡，即

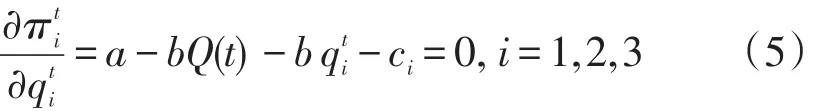
求解（5）式可得三寡头古诺纳什均衡为：

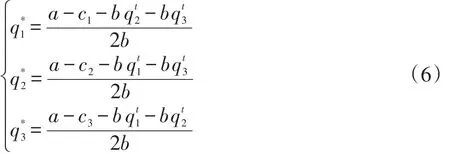
方程（6）表示在固定时期内，给定两家天然气企业产量的情况下，另一家天然气企业实现利润最大化的最优产量。从（6）式中也可以看出，古诺博弈模型是基于完全信息假设下进行的，及任何一家企业的行为都能被其他企业完全掌握，因此上式中各企业的产量是关于其他企业产量的函数，因此天然气企业在对自身产量做决策时要尽可能多的去获取或者判断有关另外两家企业产量的信息，如此才能使自己的决策更准确。

在经济模型中，“预期”起着重要的作用，预期是各经济主体基于自身的认知能力并结合当下的发展形势对未来发展趋势做出的判断，因此也可也说预期连接着经济体的当下和未来，常见的预期包括：静态预期、适应性预期和有限理性预期［2］。在古诺模型中寡头企业简单地以竞争对手当期的产量为依据，以此来估计和判断未来的经济形势，以确定下一期的产量，这种预期为静态预期。静态预期是在“蛛网模型”基础上提出来的最为单纯、把现期实际值完全当成下期预测的机制［7］。所谓的适应性预期是指经济主体依据当前的市场情形并结合过去的预测经验（包括成功的预测经验和对以往预测失败的修正）而对未来进行判断的一种机制。有限理性预期是指经济主体在尽可能收集一切能够获知的有用信息基础上对不确定市场变化做出的研判，以此来规避风险或者是实现利润最大化的决策形式。

现实生活中，受制于管理层的认知水平、获取信息的能力和企业所处市场竞争激烈程度、规模经济效应等条件限制，不同企业对未来市场变化会有不同的判断，因此也会有不同的决策类型即拥有不同的预期［2］。因此本文假设三家天然气企业在做决策时采用差异化的预期规则。

假设天然气企业1由于各种条件限制（包括市场占有率、企业获取信息能力、资源占有优势等）采取静态预期，即

第二家天然气企业在做出下期产量决策时会参考之前所做预测经验，故采用自适应预期，应用文献［10］中的模型，即α为第二家天然气企业的反馈系数。第三家天然气企业采取有限理性预期，决策模型为［11］：

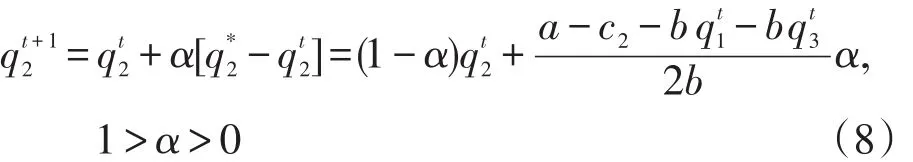
其中，β为产量调整速率，企业根据当期的边际利润来决策下期产量，即当期边际利润为正时，表明当期的产量偏低，下一期则相应的提高产量；反之当边际利润为负时，下一期减少产量。

根据式（7）、（8）、（9）可得天然气市场基于不同预期规则的三寡头动态博弈模型：

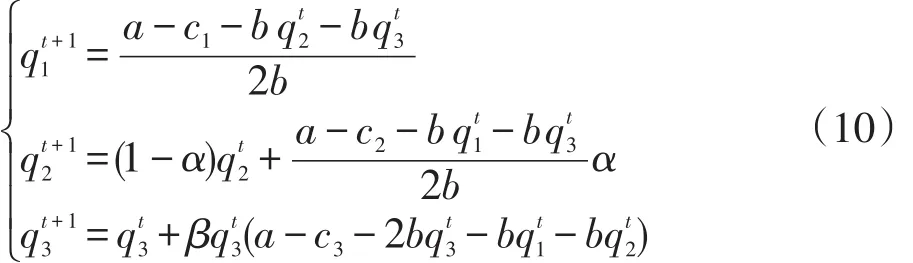
为了方便分析系统（10）的复杂动力学现象，尤其是为了对系统的稳定性和混沌现象进行严格数学证明，对系统做如下变换：

由于系统（10）和（11）是等效的，故对系统（10）的动力学性质分析可以转化为对系统（11）的动力学性质研究。

三、博弈模型复杂动力学分析

本节将应用非线性动力系统理论相关知识，对系统（11）的局部动力学和混沌存在性进行研究。求解系统的均衡解，并应用数学推理证明Nash均衡点的存在性及系统局部稳定性，最后利用数值模拟验证推理的正确性，同时利用Lyapunov指数和吸引子分维数判定系统存在混沌现象。

（一）不动点与局部稳定性分析

定义集合：

定理1：当a＞ci，i=1，2，3，且（α，β）∈Ω1，（a，c1，c2，c3）∈Ω2时，系统（11）存在2个非负均衡点。

证明：令X（t+1）=X（t），Y（t+1）=Y（t），Z（t+1）=Z（t）可解得系统（11）的两个均衡解，即

因为有（a，c1，c2，c3）∈Ω2，即

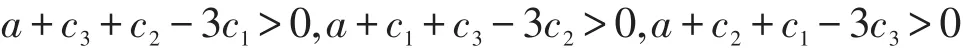
所以X*＞0，Y*＞0，Z*

则均衡点E0、E*均为非负，且E0为有界均衡点，E*为Nash均衡点。

为了研究系统不动点的局部稳定性，计算出系统（11）的Jacobi（雅克比）矩阵：

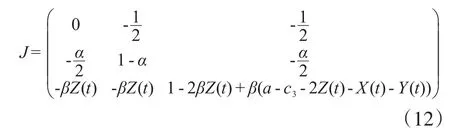
定理2：当（α，β）∈Ω1，（a，c1，c2，c3）∈Ω2时，系统（11）的有界均衡点E0为不稳定的鞍点。

证明：由（12）式可知，系统（11）在有界均衡点E0处的雅克比矩阵为：

其特征多项式为：

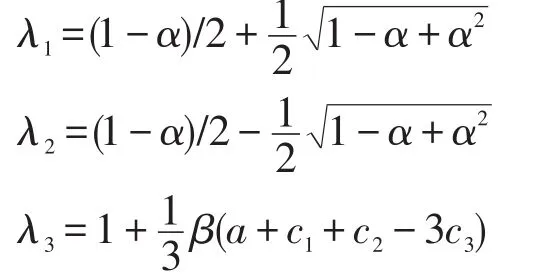
根据文献［12-13］可知，如果系统（11）在均衡点E0处对应的特征方程的所有特征值λi满足|λi|＜1，i=1，2，…，n时，此均衡点才是稳定的。

当（α，β）∈Ω1，（a，c1，c2，c3）∈Ω2时，有0＜λ1＜1，0＜λ2＜1，λ3＞1，意味着系统在E0处不满足所有的特征值绝对值都小于1，故有界均衡点E0是不稳定的鞍点。

为了接下来证明系统在均衡点E*处的稳定性，现给出一条引理：

引理1：设多项式 f（x）=x3+a1x2+a2x+a3，则有［14］：

（1）若 f（x）的系数满足 1+a1+a2+a3＜0或1-a1+a2-a3＜0，则 f（x）=0至少有一个根的绝对值大于1。

（2）若f（x）的系数同时满足以下条件：

则 f（x）=0的所有根（实数或者复数根）的绝对值都小于1。

证明：系统（11）在均衡点E*处的雅克比矩阵为：

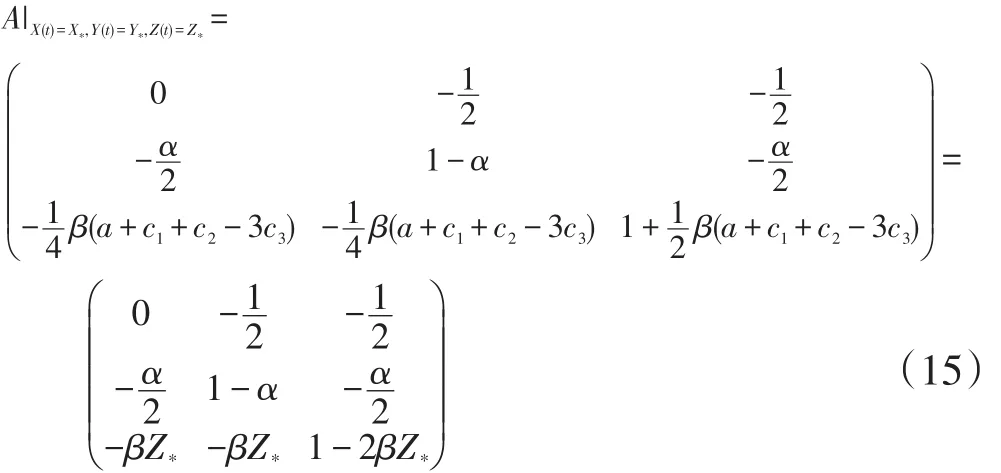
其特征多项式为：

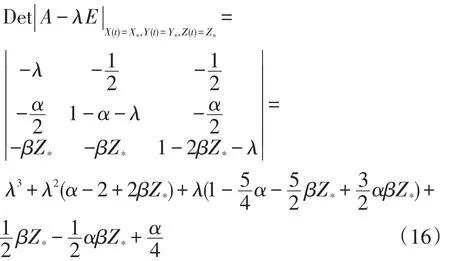
故系统（11）在E*的特征方程具有如下形式：

其中：

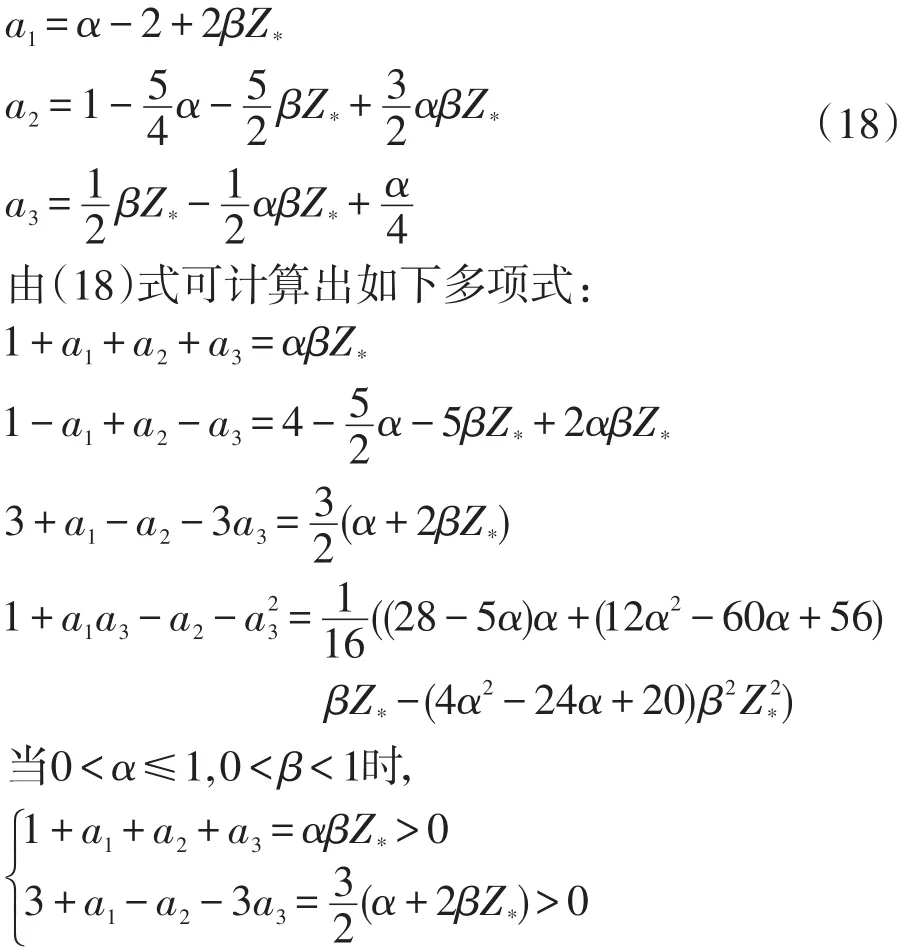
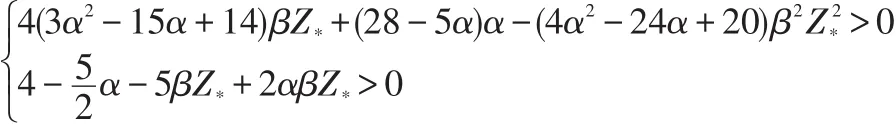
则系统（11）在Nash均衡点E*处对应的特征方程的根的绝对值都小于1，故此时均衡点E*是稳定的，证明完毕。

（二）系统局部动力学数值模拟

本节通过对系统（11）进行数值模拟，来验证理论推理的正确性，并分析系统在不同参数取值情况下的分岔、混沌吸引子和初值敏感性（蝴蝶效应）等特征。

参数取值：a=8，c1=4，c2=3，c3=2，此时有：

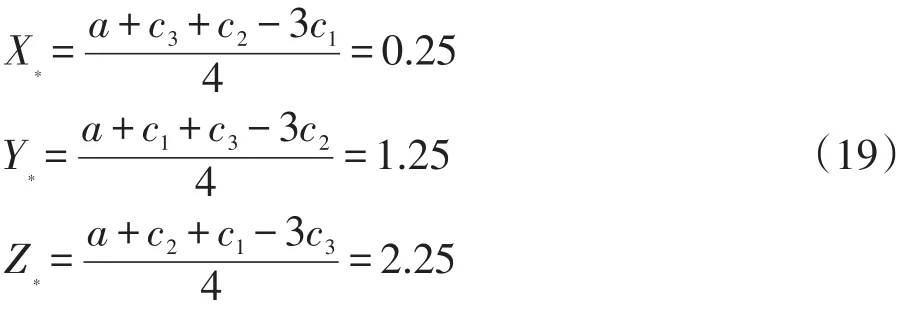
即均衡点E*=（0.25，1.25，2.25），将Z*=2.25代入定理3，得到系统（11）的稳定性判断式为：

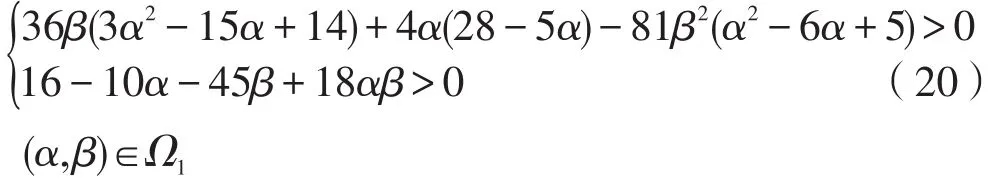
（20）式中由自适应天然气企业反馈系数α和有限理性企业产量调整系数β所构成的平面区域决定了系统的稳定区域，如图1所示。

由图1可知，当天然气企业3的产量调整速率β及企业2的产量反馈系数α的组合（α，β）处于曲线下方（及图1中所标识为稳定区域）部分时，系统（11）总是处于稳定点E*处，此时意味着三个企业的产量始终稳定在（0.25，1.25，2.25）。然而如果企业3的产量调整速率过快，市场将随着β的不断增大而逐渐步入不稳定状态，接下来以图中的四个点为例进行说明。由图1中曲线可得β的两个临界值为β=0.360 和β=0.225。当β＜0.225时，对于任意的α取值，均衡点E*总是稳定的，例如图中的A点；当0.225＜β＜0.360时，如果此时α的取值使得点（α，β）在曲线之下，则均衡点E*依旧是稳定的，例如图中C点；若（α，β）对应的点在曲线上部（如B点）则均衡点E*不稳定；当 β＞0.360，此时任意的组合点（α，β）都处于曲线上部所在的非稳定区域，如图中D点所示。所谓的稳定区域是指系统（11）在初始条件不同的情况下最终是否能归于收敛的意思，其经济学解释为：三家天然气企业在不同的初始产量下，若其产量调整速率β与产量反馈系数α的组合（α，β）位于稳定区域内，那么在经过有限次数的博弈之后三家天然气企业的产量终归平衡于稳定点（0.25，1.25，2.25）处；反之当天然气企业产量调整参数组合位于曲线上部的非稳定区域时，无论经历多少次的博弈，各企业的产量依旧不会稳定于一点，此时各企业的产量将一直处于波动状态，整个天然气市场也很有可能进入无序竞争状态，即所谓的混沌状态。

1.各天然气企业的产量分岔图

刚刚分析了在天然气企业产量调整参数取值不当时可能导致整个市场进入混沌状态，为了进一步地分析系统（11）的混沌特性，下面给出了各企业产量随参数α、β变化的分岔图，图2和图3分别是β=0.2和 β=0.3时系统（11）随参数α变化的分岔图；图4为α=0.3时系统（11）关于 β变化的分岔图。参数取值依然为：a=8，c1=4，c2=3，c3=2，三家天然气企业初始产量依次取值0.1、0.2、0.3。

图2　　β=0.2时各天然气企业产量随参数α变化的分岔图

从图2可知，当β=0.2时，系统（11）中各天然气企业的产量在整个α∈（0，1）区间内一直稳定在均衡点E*=（0.25，1.25，2.25）。结合图1可知，由于 β=0.2小于临界值0.225，故在整个α变化区间内系统都稳定在E*处，这表明图1和图2是一致的。为了进一步验证图1的正确性，在0.225＜β＜0.360区间内另取一个 β值画出系统（11）中各天然气企业的产量分岔图，如图3所示。

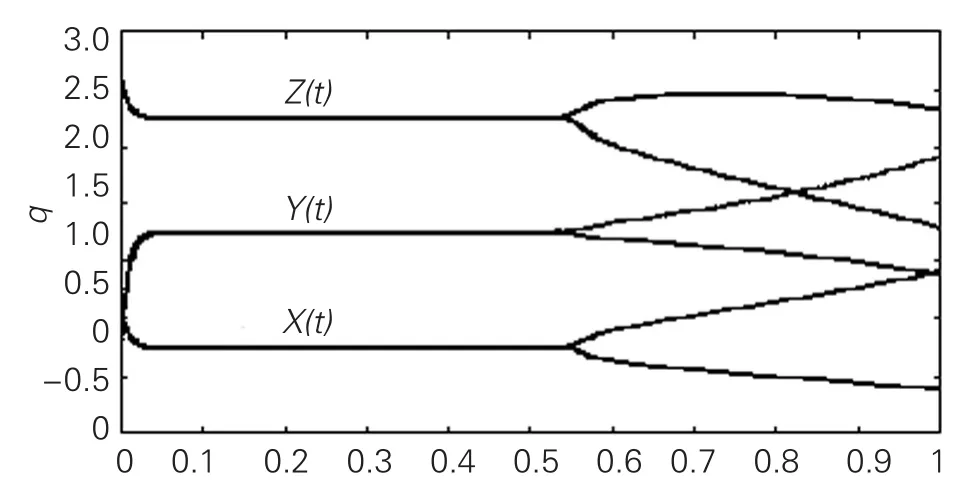
图3　　β=0.3时各天然气企业产量随参数α变化的分岔图

从图3可以看出，当0＜α＜0.54时，系统依旧稳定在均衡点E*=（0.25，1.25，2.25）处；当α≥0.54时系统出现分岔，从稳定状态转变为二倍周期状态。从图1中也可以看出，在β=0.3时，系统的稳定区域为0＜α＜0.54，这表明图3和图1也是一致的。

从图4可知，当0＜β＜0.325时，系统稳定在均衡点E*=（0.25，1.25，2.25）处；当 β=0.325时，系统出现分岔。这依然和图1是一致的。从β≥0.325开始，系统出现倍周期分岔现象，依次进入2周期、4周期、8周期……当 β＞0.540时，系统彻底进入混沌状态。结合上述四幅图可得出结论：自适应预期天然气企业的反馈参数α越小，越有利于维护市场的稳定；而采取有限理性预期的天然气企业对市场的稳定性影响最为显著，其产量调整速率应当控制在一个合理的区间，一旦调整速率过快将很可能导致整个天然气市场从稳定状态进入无序竞争状态。综上所述，在不同预期决策规则下，企业自身的决策对整个市场的影响差异很大，且整个市场的稳定性将变得更加难以控制，若彼此之间的竞争处于合理状态那么整个市场很可能会一直处于有序竞争状态；反之一旦某些企业采用激进的竞争策略，很可能导致整个市场出现巨幅震荡，进入混沌状态。

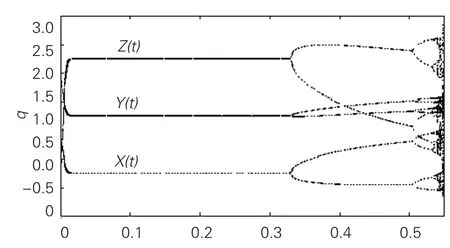
图4　α=0.3时各天然气企业产量随参数β变化的分岔图

2.系统混沌的判定

（1）李雅普诺夫（Lyapunov）指数。李雅普诺夫指数是刻画动力系统中两条相互靠近的轨道沿某特定方向按指数相互分离或靠拢的速率，它是判定动力系统是否出现混沌现象的重要定量指标。当系统的最大李雅普诺夫指数为负值时表明系统处于稳定状态；最大Lyapunov指数为零时意味着系统出现分岔；反之，正的Lyapunov指数则意味着混沌现象的出现［15］。本文给出了系统在图4中的参数取值下的Lyapunov指数谱，如图5所示。

从图5中可知，在β＜0.540区间内系统最大李雅普诺夫指数为非负且出现了a、b、c、d四个零点，意味着系统发生了分岔；结合图4可知，在a点（即图4中β=0.325的点）系统从稳定状态进入二倍周期，依次在b、c、d三个零点进入四倍周期、八倍周期、十六倍周期；当 β＞0.540时，系统最大李雅普诺夫指数为正，系统进入混沌状态。因此图5和图4是一致的，由此说明系统确实产生了混沌现象。

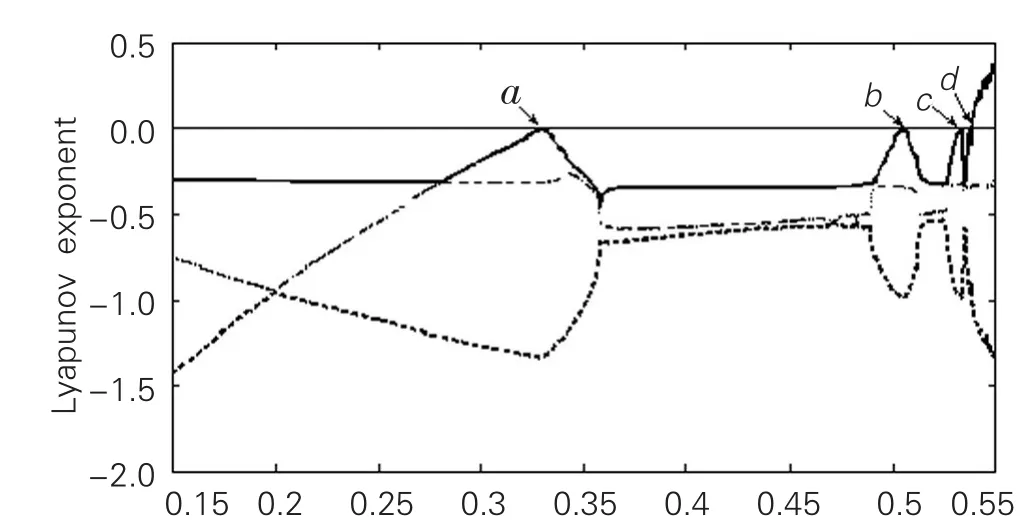
图5　a=8，c1=4，c2=3，c3=2，α=0.3时系统（11）的Lyapunov指数谱

（2）混沌吸引子与分维数。在系统产生混沌现象的同时会出现混沌吸引子（奇异吸引子），而此时的混沌吸引子具有分维数特征，因此可以通过判断混沌吸引子是否具有分维数来判定混沌［16］。图6给出了系统在某些固定β时的相图及混沌吸引子。

图6给出了系统的相图，通过图6（a）到（e）可观察到周期1轨、周期2轨、周期4轨、周期8轨及周期16轨，（f）为系统的混沌吸引子。从图5中可知，系统在（f）下的李雅普诺夫指数分别为：

图6　a=8，c1=4，c2=3，c3=2，α=0.3系统在固定β取值下的相图及混沌吸引子

由Lyapunov指数可以计算出混沌吸引子的Kaplan-Yorke维数，记为Dky，其表达式如下：

其中，k等于满足∑ki=1λi≥0的最大的i值（λi按Lyapunov指数降序排列）［17］。通过观察可知在上述的三个李雅普诺夫指数取值下k=2，则图6（f）中混沌吸引子的Kaplan-Yorke维为：

因此（f）的混沌吸引子具有分维数，系统的确处于混沌状态。

（3）各企业产量对初值的敏感性。所谓的初值敏感性又称之为“蝴蝶效应（The Butterfly Effect），是指在动力系统中，初始条件的微小差别通过有限次的运动和迭代之后将使最终结果产生巨大的偏差［6］。

为分析系统（11）中各天然气企业产量对初值的敏感性特征，在图4中系统处于混沌状态（α=0.3，β≥0.540）的基础上，将天然气企业3的初始产量由Z（1）=0.3增加到Z'（1）=0.300 01，图7-9展示了这种微小变化对系统的影响。

图7　α=0.3，β=0.545时天然气企业1产量对初值变化的敏感性

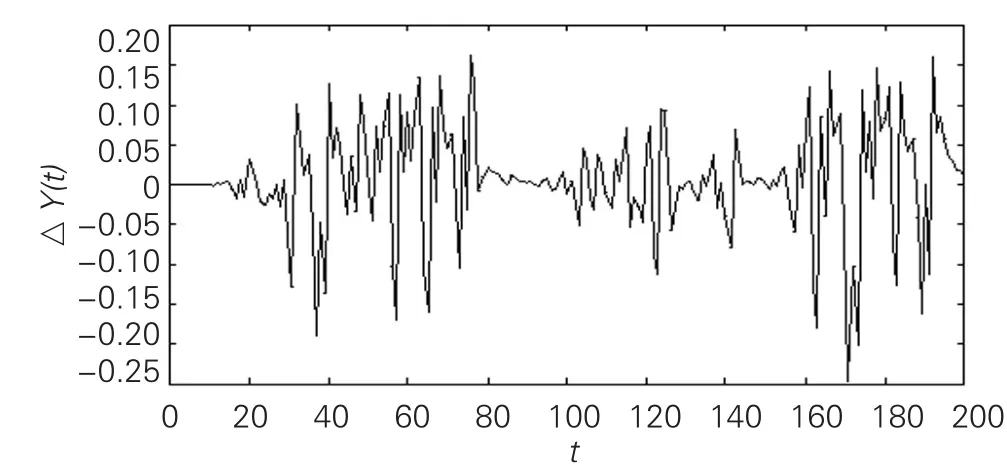
图8　α=0.3，β=0.545时天然气企业2产量对初值变化的敏感性

图9　α=0.3，β=0.545时天然气企业3产量对初值变化的敏感性

由图7-9可知，企业3产量0.000 01的微小变化经过有限次迭代之后，将会对三家企业的产量产生明显的影响，企业1前后产量的变化幅度为（-0.4，0.5），企业2产量变化幅度为（-0.25，0.17），企业3产量变化幅度为（-1.25，1.7）。从系统对初值的敏感性可知，当市场处于混沌状态时，任何一家天然气企业产量的微小变化都会对其他企业产量产生巨大影响。因此在混沌市场状态下，企业就更难对未来市场的变化做出准确的判断，其关于产量的决策就更加无据可依。

（三）系统混沌控制

在现实中，企业间的过度竞争容易导致市场无序行为的出现，这不仅损害了在位企业的利益，长远来看这种不确定的竞争也不利于市场规范。因此采取能够有效稳定市场、防止混沌现象出现的措施尤为必要。

本文采用文献［18］中的时滞反馈机制对系统（11）进行混沌控制，时滞反馈方法为：

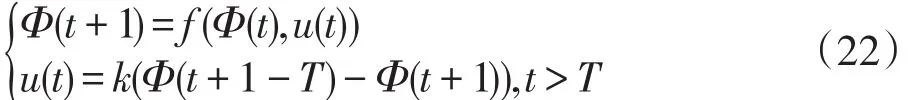
其中，T为引入时滞；k为控制系数。由于天然气企业3的产量调整速率β对系统的稳定性影响最为明显，故文章采取对天然气企业3进行时滞反馈控制。将（22）代入系统（11）并令T=1，得到采取混沌控制后的系统如下：

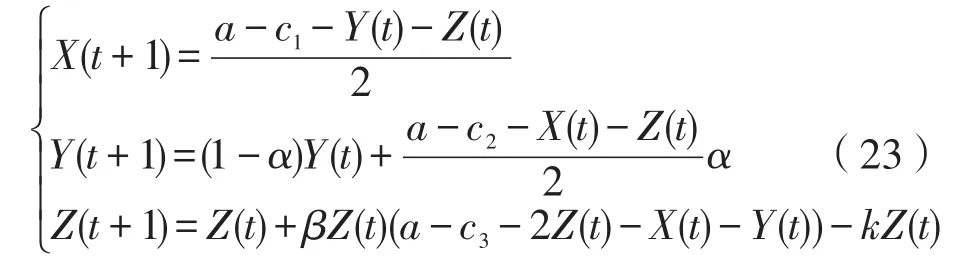
由图4可知，当α=0.3、β≥0.540时系统处于混沌状态，因此本文取参数α=0.3、β=0.550时进行混沌控制，其余参数依旧取a=8、c1=4、c2=3、c3=2，各天然气企业初始产量分别为0.1、0.2、0.3，引入混沌控制后的系统（22）其产量随控制参数k变化的分岔图如图10所示。

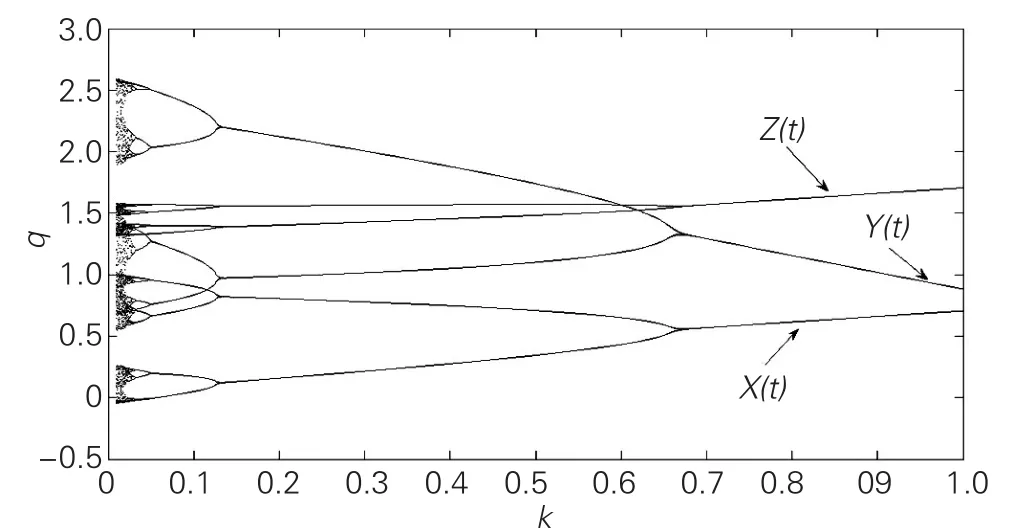
图10　α=0.3，β=0.550时系统（22）随控制系数k变化的产量分岔

从图10中的产量分岔图来看，随着控制系数k的不断增大，系统从混沌状态逐渐进入倍周期，当k＞0.68时分岔现象消失，系统进入稳定状态，说明引入时滞反馈后系统的稳定性得到有效控制，市场又重新恢复到有序状态。

四、结束语

本文将混沌经济学理论应用到我国天然气上游（供气）市场，构建了不同预期决策规则下的三寡头动态博弈模型，最后通过严格的数学推理及详细的数值模拟揭示了博弈系统复杂的动力学特性。从中得出结论：采取自适应预期的天然气企业对市场具有稳定效应，其反馈参数越小，市场越稳定；而有限理性天然气企业的产量调整速率会极大地影响市场的稳定性，过大的产量调整速率会导致市场进入混沌状态，在此状态下经济系统存在“蝴蝶效应”，即任何一个企业微小的产量调整都会引起自身及其他企业产量的大幅波动，导致企业更难把握未来市场的变化，不利于企业的长期规划和市场规范。本文最后引入了时滞反馈机制对系统进行混沌控制，使市场重新回到有序的竞争状态。研究结果期待能为我国天然气市场供气企业的产量决策提供参考。

参考文献：

［1］杨世旭，段万春，孙永河，等.基于混合策略的电信企业竞合博弈分析［J］.经济问题探索，2014（8）：179-183.

［2］浦小松.一类寡头垄断市场产量博弈及混合模型的动力学研究［D］.天津：天津大学，2012.

［3］Agiza H N，Hegazi A S，Elsadany A A.Complex dynamics and synchronization of a duopoly game with bounded rationality［J］.Mathematics&Computers in Simulation，2002，58 （2）：133-146.

［4］Bischi G I，Kopel M.Equilibrium selection in a nonlinear duopoly game with adaptive expectations［J］.Journal of Economic Behavior&Organization，2001，46（1）：73-100.

［5］Agiza H N，Elsadany A A.Nonlinear dynamics in the Cournot duopoly game with heterogeneous players［J］.Physica A Statistical Mechanics&Its Applications，2002，320（1/4）：512-524.

［6］张骥骧，达庆利，王延华.寡占市场中有限理性博弈模型分析［J］.中国管理科学，2006，14（5）：109-113.

［7］吉伟卓，马军海.发电市场不同决策规则三寡头博弈模型研究［J］.系统工程学报，2008，23（3）：257-263.

［8］Chen F，Ma J H，Chen X Q.The study of dynamic process of the triopoly games in chinese 3G telecommunication market［J］.Chaos Solitons&Fractals，2009，42（3）：1542-1551.

［9］Ma J H，Ji W Z.Complexity of repeated game model in electric power triopoly［J］.Chaos Solitons&Fractals，2009，40 （4）：1735-1740.

［10］Dubiel-Teleszynski T.Nonlinear dynamics in a heterogeneous duopoly game with adjusting players and diseconomies of scale［J］.Communications in Nonlinear Science& Numerical Simulation，2011，16（1）：296-308.

［11］Ding Z，Hang Q，Tian L.Analysis of the dynamics of Cournot team-game with heterogeneous players［J］.Applied Mathematics&Computation，2009，215：1098-1105.

［12］Mahmoud E E.Dynamics and synchronization of new hyperchaotic complex Lorenz system［J］.Mathematical& Computer Modelling，2012，55（7/8）：1951-1962.

［13］Li Y，Liu X，Chen G，et al.A new hyperchaotic Lorenztype system：Generation，analysis，and implementation［J］. International Journal of Circuit Theory&Applications，2011，39（8）：865-879.

［14］谢丽凡.不同预期的寡头博弈模型的复杂动力学研究［D］.广州：华南理工大学，2015.

［15］张晓丹，李志萍，张丽丽.一类基于奇异值分解的Lyapunov指数计算方法［J］.北京科技大学学报，2005，27（3）：371-374.

［16］Elabbasy E M，Elsadany A A，Zhang Y.Bifurcation analysis and chaos in a discrete reduced Lorenz system［J］.Applied Mathematics&Computation，2014，228（9）：184-194.

［17］Kaplan J L，Yorke J A.Chaotic behavior of multidimensional difference equations［J］.Computer Communications，2006，31（3）：576-590.

［18］Pyragas K.Continuous control of chaos by self-controlling feedback：stabilization of unstable periodic and aperiodic orbits［C］//SPIE's 1993 International Symposium on Optics，Imaging，and Instrumentation.International Society for Optics and Photonics，1993：148-159.

［责任编辑：余志虎］

中图分类号：F206；F271.5

文献标志码：A

文章编号：1007-5097（2016）08-0007-09

收稿日期：2016-04-03

基金项目：国家自然科学基金项目（71133007）；国家自然科学基金面上项目（71373297）；国家社会科学基金重点项目（15AZD014）

作者简介：杨俊（1972-），男，重庆铜梁人，教授，博士生导师，研究方向：能源技术经济，行业经济与企业发展战略；张亚军（1992-），男，重庆巫溪人，硕士研究生，研究方向：天然气市场交易与定价机制设计；张小漫（1992-），女，湖北荆州人，硕士研究生，研究方向：企业战略管理。

A Study of Three Oligopolistic Firms Game Model Based on Different Expectation Rules in Natural Gas Supply Market

YANG Jun，ZHANG Ya-jun，ZHANG Xiao-man
（School of Economics and Business Administration，Chongqing University，Chongqing 400044，China）

Abstract：A three oligopolistic firms dynamic game model based on different expectation rules was established in the upstream market of natural gas（gas supply）.The system equilibrium was calculated by chaos theory of economics and then analyzed the stability of the system.In the end，the paper analyzed the complex dynamic behavior of the system deduced by the change of main-parameters by the numerical simulation method.The results show that the game model has a very complicated dynamic behavior.Adaptive firms have a stabilizing effect on the market，and the fast output adjustment rate of limited rational firms will lead to the market to enter the chaotic state.

Keywords：natural gas；game model；expectation；chaos