非负弱下鞅的极大值不等式
冯德成,王晓艳,高玉峰
(西北师范大学数学与统计学院,甘肃兰州 730070)
非负弱下鞅的极大值不等式
冯德成,王晓艳,高玉峰
(西北师范大学数学与统计学院,甘肃兰州730070)
给出了两个初等不等式,并运用此不等式得到了非负弱下鞅的极大值不等式.
初等不等式;非负弱下鞅;极大值不等式
1 预备知识
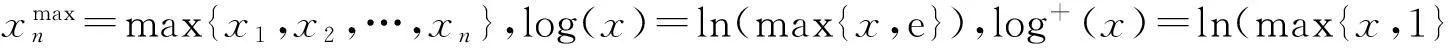
定义1设{Sn,n≥1}是一列L1随机变量,如果对任意1≤i 其中g是任意分量不减的函数且使得上述期望有意义,那么称{Sn,n≥1}是一个弱鞅.进一步,若g是一个非负函数,则称{Sn,n≥1}是一个弱下鞅. 弱鞅的概念是由Newman和Wright[1]于1982年首先提出的.2000年,Christofides[2]将下鞅的Chow极大值不等式推广到弱下鞅的情形.2004年,Wang[3]给出了弱鞅的极大值不等式,推广并改进了Christofides的结果.2013年,Acciaio等[4]利用实数中的一些初等不等式给出了非负下鞅的Doob型Lp极大值不等式.2012年,Prakasa得到了下列非负弱下鞅的两个极大值不等式: 定理A设{Si,1≤i≤n}是一个非负弱下鞅,则对任意的n≥1,有 (1) (2) 受文献[5]的启发,本文首先给出两个初等不等式,并运用此不等式得到非负弱下鞅的另一种形式的极大值不等式. 下面给出两个初等不等式. 命题1设x1,x2,…是一列非负实数. ( i )令h(x)=-log+(x),则 (3) ( ii )当1 (4) 证明(i)由引理1,有 由函数x|→xlog+(x)在x≥0处的凸性,有 整理上式,有 移项整理,既得(3)式. (ii)对任意的1 对上式两端求和,并运用引理1就有 (4)式得证.】 定理1设{Sn,n≥1}是一个非负弱下鞅,则对任意的n≥1,有 (5) (6) 证明对非负弱下鞅{Sn,n≥1}运用(3)式,可知 (7) 上式也可改写成 (8) 对(7)式两端同时求期望,可得 再结合(8)式,有 由此(5)式得证. 对非负弱下鞅{Sn,n≥1)}运用(4)式,得 将(7)式代入上述不等式,就有 (9) (10) 对(9)式两端同时求期望,再结合(8)和(10)式,就有 (6)式得证.】 推论1设{Sn,n≥1}是一个非负弱下鞅,则对任意的n≥1,有 证明对于任意的x≥0,有 取x=e/c,c≥0,则 c-clog+c≤1. 对于非负弱下鞅{Sn,n≥1}中的S1运用上式,即有 S1-S1log+S1≤1a.s. 上式两端求期望,就有 (11) 将(11)式代入(5)式,就有 结论得证.】 [1]NEWMANCM,WRIGHTAL.Associatedrandomvariablesandmartingaleinequalities[J].Zeitschrift ür Wahrscheinlichkeitstheorie und Verwandte Gebiete,1982,59(3):361. [2]CHRISTOFIDESTC.Maximalinequalitiesfordemimartingalesandastronglawoflargenumbers[J].Statistics and Probability Letters,2000,50(4):357. [3]WANGJian-feng.Maximalinequalitiesforassociatedrandomvariablesanddemimartingales[J].Statistics and Probability Letters,2004,66(3):347. [4]ACCIAIOB,BEIGLBOCKM,PENKNERF,etal.AtrajectorialinterpretationofDoob’smartingaleinequalities[J].The Annals of Applied Probability,2013,23(4):1494. [5]PRAKASAR.Remarksonmaximalinequalitiesfornon-negativedemisubmartingales[J].Statistics and Probability Letters,2012,82(7):1388. (责任编辑马宇鸿) Maximal inequalities for non-negative demisubmartingales FENG De-cheng,WANG Xiao-yan,GAO Yu-feng (College of Mathematics and Statistics,Northwest Normal University,Lanzhou 730070,Gansu,China) The two elementary inequalities are given firstly,and the maximal inequalities for non-negative demisubmartingales is given by using these two elementary inequalities. elementary inequality;non-negative demisubmartingale;maximal inequality 10.16783/j.cnki.nwnuz.2016.04.004 2015-10-30;修改稿收到日期:2016-04-01 国家自然科学基金资助项目(11461061);西北师范大学青年教师科研能力提升计划项目(NWNU-LKQN-11-2) 冯德成(1972—),男,甘肃武威人,副教授,博士.主要研究方向为随机分析和应用概率. E-mail:fengdc@163.com O 211.4 A 1001-988Ⅹ(2016)04-0014-03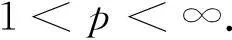
2 主要结论


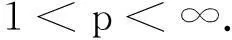
——2018年全国高考Ⅲ理科数学21题别解

