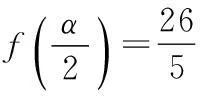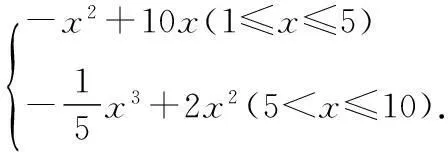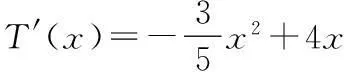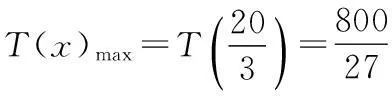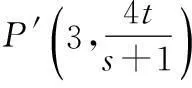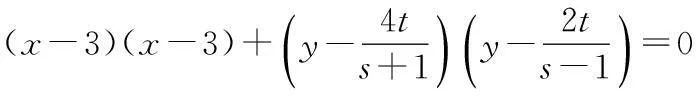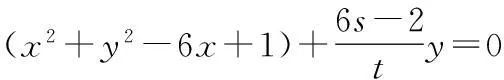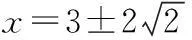高二数学测试



高二数学测试

一、填空题(本大题共14小题,每小题5分,共70分)

1.已知集合U=R,集合M={y|y=2x,x∈R},集合N={x|y=lg(3-x)},则(UM)∩N=______.

3.命题p:∀x∈R,x2+1>0的否定是______.

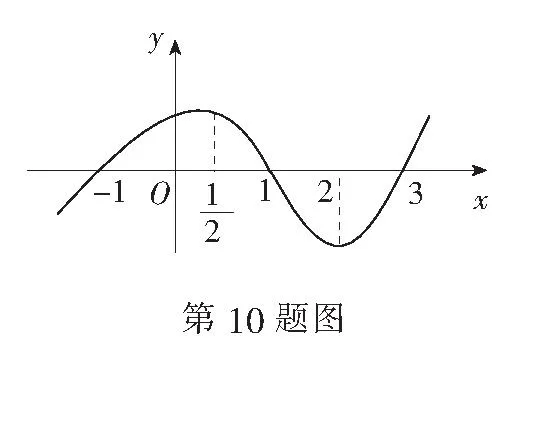
4.“p:x∈{x|x2-x-2≥0}”,“q:x∈{x|x

7.定义在R上的函数f(x)满足f(x+2)f(x)=1,当x∈[-1,1)时,f(x)=log2(4-x),则f(2 016)=______.

9.与圆x2+(y-2)2=2相切且在两条坐标轴上的截距相等的直线有______条.

10.已知函数y=f(x)(x∈R)的图象如图所示,则不等式xf′(x)<0的解集为______.

11.已知直线ax+y-1=0与圆C:(x-1)2+(y+a)2=1相交于A,B两点,且∆ABC的面积最大,则实数a的值为______.

12.y=2sin x+sin 2x的值域是______.

二.解答题(本大题共6小题，共90分.解答应写出必要的文字说明、证明过程或演算步骤)

15.(本小题满分14分)已知集合A={x|x2-2x-a2-2a<0},B={y|y=3x-2a,x≤2}.

(1)若a=3,求A∪B;

(2)若A∩B=A,求实数a的取值范围.

(1)求函数f(x)的最小正周期和单调递增区间;

目前,每生产1万件合格的产品可以盈利10万元,但每生产1万件次品将亏损40万元.

(1)试将生产这种产品每天的盈利额T(万元)表示为日产量x(万件)的函数;

(2)问当生产这种产品的日产量x约多少时(精确到0.1万件),企业可获得最大利润?

19.(本小题满分16分)已知圆O的方程为x2+y2=1,直线l1过点A(3,0)，且与圆O相切．

(1)求直线l1的方程;

(2)设圆O与x轴交与P,Q两点,M是圆O上异于P,Q的任意一点,过点A且与x轴垂直的直线为l2,直线PM交直线l2于点P′,直线QM交直线l2于点Q′．求证:以P′Q′为直径的圆C总过定点,并求出定点坐标.

(1)若a=2,求函数f(x)在(1,f(1))处的切线方程;

(2)若函数f(x)在(1,+∞)上为增函数,求a的取值范围;

(3)若a≠0,讨论方程f(x)=0的解的个数,并说明理由.

参考答案

一、填空题

1.(-∞,0]；2.1；3.∃x∈R,x2+1≤0；

13.a>e;14.a<2.

二、解答题

15.(1)将a=3代入A中不等式，得

x2-2x-15<0,

解得-3

将a=3代入B中等式，得y=3x-6,

∵x≤2,∴0<3x≤9,

即-6<3x-6≤3,

∴B=(-6,3],A∪B=(-6,5).

(2)∵A∩B=A,∴A⊆B,

由B中y的范围为-2a

由A中不等式变形，得

x2-2x+1-a2-2a-1<0,

即(x-1)2-(a+1)2<0,

整理得(x+a)(x-a-2)<0.

∵A∩B=A,∴A⊆B,

当a=-1时,A=∅,满足题意;

当a+2>-a,即a>-1时,A=(-a,a+2).

A=(a+2,-a).∵A⊆B,

=cos xcos 20°-sin xsin 20°+cos xcos 20°+sin xsin 20°,

=2cos xcos 20°,

18.(1)设盈利额T(万元)关于日产量x(万件)的函数为T(x),则

T(x)=x(1-P)×10-xP×40

=x(10-50P).

当1≤x≤5时,

=-x2+10x;

当5

(2)当1≤x≤5时,T(x)max=T(5)=25;

当5

∵T(x)的图象在(5,10]上连续,

∴T(x)在(5,10]上的最大值

答:当生产这种产品的日产量约为6.7万件时,企业可获得最大利润.

19.(1)∵直线l1过点A(3,0),且与圆C:x2+y2=1相切.

设直线l1的方程为y=k(x-3),即kx-y-3k=0,

则圆心O(0,0)到直线l1的距离为

∴以P′Q′为直径的圆C′的方程为

又s2+t2=1,整理得

即a≤x2在x∈(1,+∞)恒成立,故a≤1,经检验,符合题意,∴a≤1.

② a>0时,

综上，0

a<0或a=e时,f(x)有唯一解;

a>e时,f(x)=0有2个解.