三点共线定理的推论及妙用
2016-08-31 03:35陈玉兰吴志鹏
高中数学教与学 2016年15期
陈玉兰 吴志鹏
(福建省德化第一中学,362500)
三点共线定理的推论及妙用
陈玉兰吴志鹏
(福建省德化第一中学,362500)
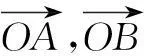
证明t=0时,结论显然成立.
t≠0时,证明过程如下:
因为C,A,B三点共线,所以
即m+n=t.

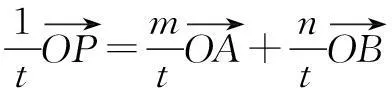
连结OP交直线AB于点C,则由三点共线定理可知
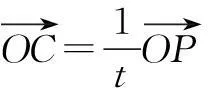
综上,得证.
该结论作为三点共线定理的推广,可妙解诸多与向量相关的问题.现在举例如下:
一、妙解系数和问题
例1如图1,已知四边形ABCD中,AB∥CD,AB=2CD,M,N分别是CD,BC的中点,若
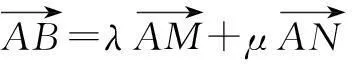
解延长AB交MN的延长线于E点,此时M,N,E三点共线.
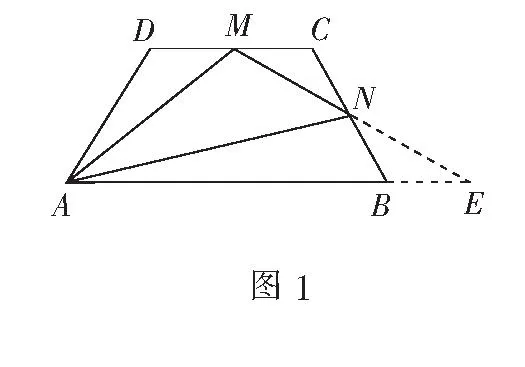
因为AB∥CD,N是BC的中点,易知∆NCM≌∆NBE,所以MC=BE.
因为M是CD的中点,且AB=2CD,所以
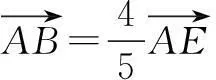
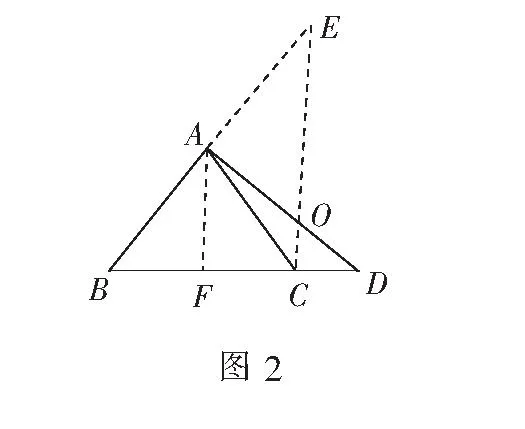
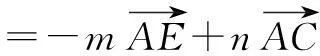
连结EC交AD于点O,此时E,O,C三点共线.过点A作AF∥EC,并交BC于F,由于A为BE的中点,则F为BC的中点.
因为BC=3CD,所以
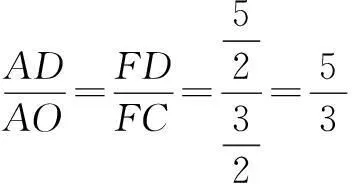
二、妙解向量问题
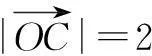
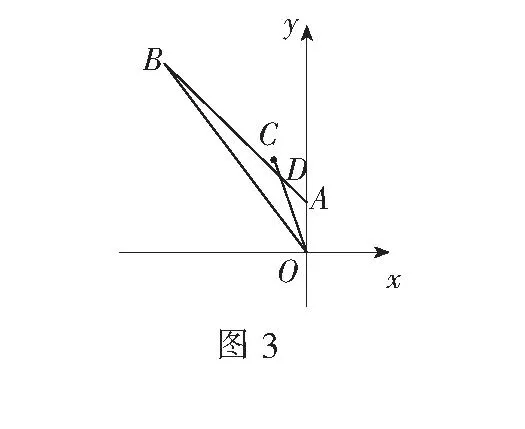
解如图3,连结OC交AB于D点.因为OC为∠AOB的平分线,故可令
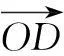
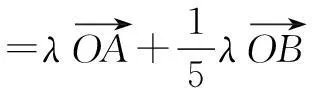
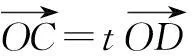
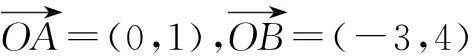
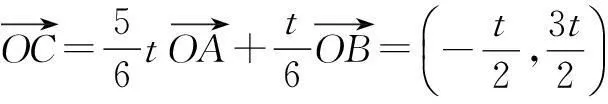
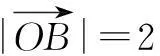
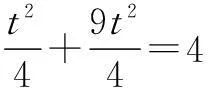
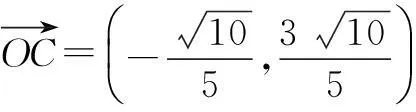
三、妙解线段比问题
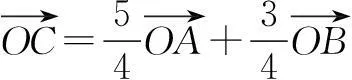
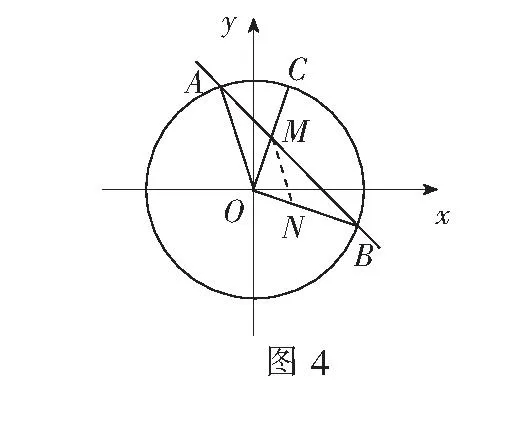
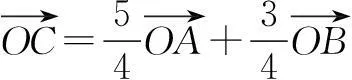
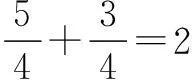
过点M作MN∥OA,交OB于点N.
在Rt∆OMB中,
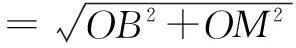
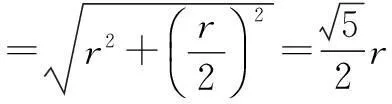
四、妙解面积比问题
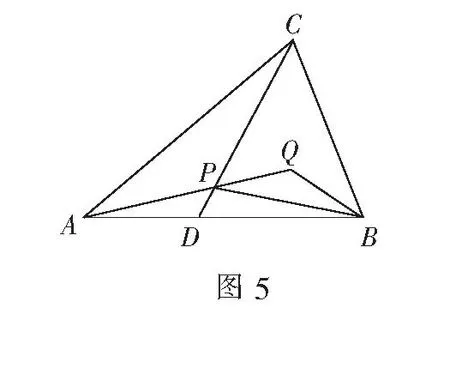
解延长CP交AB于点D.
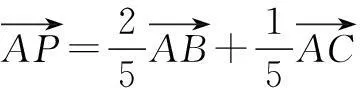
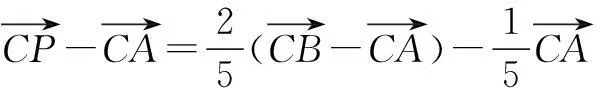
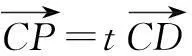
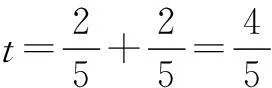
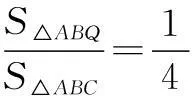
故选D.

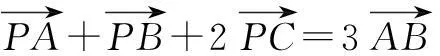
(A)3(B)4(C)6(D)9
上述两题用此法求解简单方便,有兴趣的读者可动手试一试.
五、妙解最值问题
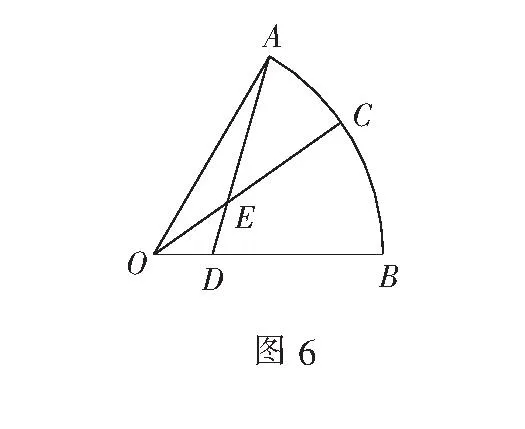
连结AD交OC于点E,此时A,E,D三点共线.
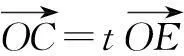
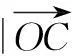
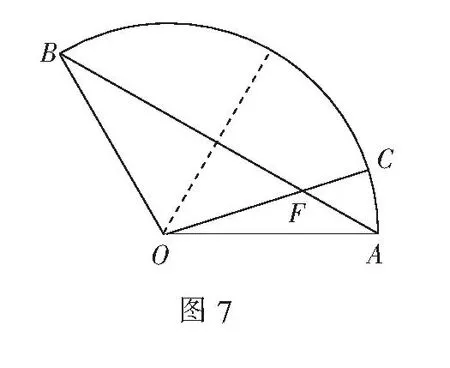
解设OC与AB交于点F,则O,F,C三点共线.
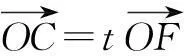
由上述结论知x+y=t.
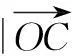
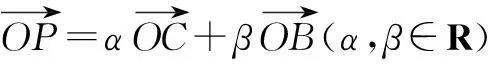
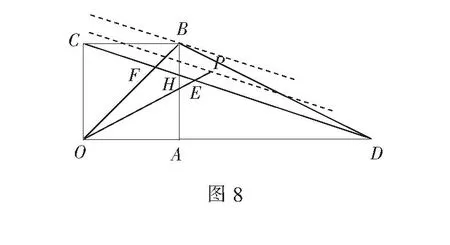
解连结OP交CD于点E,此时C,E,D三点共线.
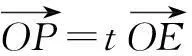
因为点P为∆BCD内(含边界)的动点,移动直线l,当直线l过点B时,t有最大值.
连结OB交CD于点F,此时C,F,D三点共线.
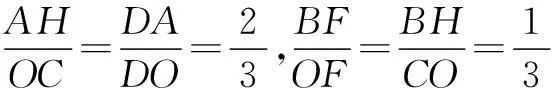
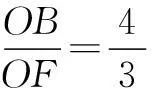
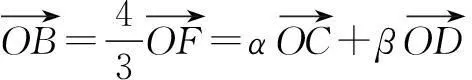
猜你喜欢
新高考·高一数学(2022年3期)2022-04-28
中等数学(2021年4期)2021-08-14
中学生数理化·高一版(2021年5期)2021-07-21
数学小灵通(1-2年级)(2020年6期)2020-06-24
河北理科教学研究(2020年4期)2020-03-09
小学阅读指南·低年级版(2017年7期)2017-08-04
中学语文(2015年21期)2015-03-01
今日中学生(初三版)(2013年6期)2013-07-30
中学生数理化·高二版(2008年11期)2008-06-17

