基于改进人工蜂群算法的分布式电源规划

娄宁娜　,毛　弋,黄媛玉

(湖南大学电气与信息工程学院, 中国 长沙　410082)



基于改进人工蜂群算法的分布式电源规划

娄宁娜*,毛弋,黄媛玉

(湖南大学电气与信息工程学院, 中国 长沙410082)

通过改进人工蜂群算法, 建立了系统网损最小、电压质量最优的综合优化目标, 应用判断矩阵法确定多目标的权重系数, 进一步优化分布式电源的选址与定容.在改进的算法中, 运用均匀设计-反向寻优的方法来优化初始群体, 提高全局寻优率.同时, 为了解决基于比例适应度选择不足的问题, 用基于适应度排序的选择概率代替了基于比例适应度的选择概率, 不仅使种群的多样性得到了保护, 而且扩大了全局搜索的范围.最后采用IEEE33标准节点配电网仿真, 通过算例分析来验证该算法的有效性和可靠性.

分布式电源；人工蜂群算法；适应度排序选择；均匀设计；反向寻优

随着电力技术的不断发展和进步, 人们总是在寻求更好的办法来解决各种弊端, 电力系统规模的不断扩大和负荷的持续增加给大电网带来了诸多问题, 比如输电系统和配电系统损耗过大、电网可靠性降低、跟踪负荷变化的灵活性降低、对环境的破坏日益严重[1]等.本文通过采用分布式发电(Distributed Generation, DG)与大型电网相结合的供电方式, 提高了供电的可靠性、减轻了环境污染等, 最终实现能源的可持续发展[2-3].

分布式电源一般是指独立分散的小容量电源, 通过较小容量的发电设备(容量一般小于30 MW)为其独立供电, 来满足特定用户的需求.近几年, 越来越多的智能算法比如免疫学算法、蚁群算法等应用到DG的选址与定容.文献[4]和文献[5]对分布式电源的大小及接入点分别采用了标准的遗传算法和模糊的遗传算法进行研究.文献[6]提出了采用量子微分进化算法对分布式电源接入配电网进行优化配置.文献[7]采用粒子群算法进行寻优, 并以系统的有功网损为目标进行优化.但是, 为了获取全局最优解, 多种智能算法结合用于配电网问题造成算法的复杂性.人工蜂群(Artificial Bee Colony, ABC)算法[8]是Karaboga在2005年提出的一种新的智能算法.它最突出的特点是操作简便, 鲁棒性强.本文建立了以系统网损及节点电压为目标的优化模型, 应用判断矩阵法确定多目标的权重系数, 进一步优化分布式电源的选址与定容.传统人工蜂群算法具有收敛速度慢, 易陷入局部最优等缺点, 会发生失真现象.本文提出均匀设计-反向寻优来初始化群体, 并且采用基于排序的选择策略可以对目标进行一次搜寻, 能避免算法陷入局部最优解, 提高收敛率.

1　含分布式电源的配电网络数学模型

1.1目标函数

分布式电源的优化目标很多, 主要有系统的网络损耗最小、分布式电源的投资成本最低以及节点电压稳定等.本文以系统网损及节点电压为指标建立目标函数.

(1)有功损耗指标

表达式为

式中Ploss为配电网的有功损耗；b为配电网支路总数；rj为支路j的电阻值,Pj和Qj分别为支路j的有功功率及无功功率；Uj支路j末端节点电压幅值.

(2)节点电压指标

分布式电源的接入能够改善电压分布情况, 使电压的偏移量在很小的范围内波动.计算公式为:

式中, ΔU表示为首节点电压与电网其他电压偏差的平均值；b为节点数；Vj表示第j个节点的电压幅值；V0表示首节点电压幅值.

1.2权重系数的设置

对于多目标优化问题, 常采用对不同的目标函数进行加权求和, 转化为单目标的方法, 权重系数的设置对优化结果有直接的影响.本文采用判断矩阵法, 根据不同目标之间的两两对比, 事先对权重系数进行精确设置.

美国运筹学家Saaty提出1-9比率标度法, 作为不同目标函数间相互比较判断标准[9].如表2所示, βij为标度值, Fi和Fj为不同等级的目标函数.

表1　比率标度法的标度值及其含义

因此, 利用βij可以构成判断矩阵H,

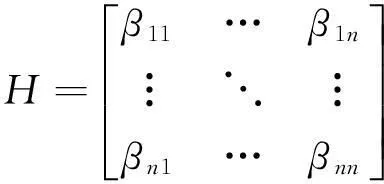
根据H, 目标Fi在整个问题中的重要程度αi可由βij的几何平均给出:

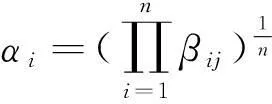
然后, 可以求取各个目标函数的权重系数:

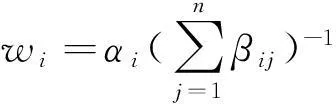
对于所提出的优化目标, 可以按照有功功率损耗及电压水平的重要性进行排序.确定权重系数之后就可以将多目标进行加权求和转化为对单目标进行优化.

1.3约束条件

含分布式电源的配电网的约束条件还包含:

(1)潮流等式约束, 系统各支路与节点须满足潮流方程.

(2)不等式约束包括、节点电压的约束、电源容量的约束、分布式电源最大安装容量约束等, 数学表达式为:

式中, UUj和ULj分别表示j节点电压变化的上限与下限；Sj为流过支路j的功率；Sjmax为支路j所通过的最大功率值；PDGmax和PDGmin分别表示节点允许接入分布式电源容量的上限与下限.

2　改进的人工蜂群算法

人工蜂群算法源于蜜蜂寻找蜜源的行为和方法而诞生的一种新型算法, 其具有操作方便, 鲁棒性较强等优点[10].然而, 该算法与其他智能算法类似, 具有过早的陷入局部收敛的缺点, 而到后期该算法收敛速度缓慢, 在系统参数比较复杂的情况下, 会造成无最优解的情况.由于这些缺点限制了ABC算法更好地发展应用, 人工蜂群算法的研究与改进成为了国内外学者研究的重要课题.

2.1分布式电源的选取

人工蜂群算法运用于分布式电源规划时需要对分布式电源的选址与容量进行编码.

C1={a1,a2,…,an}，

C2={b1,b2,…,bn}，

C={C1|C2}={a1,a2,…,an|b1,b2,…,bn}，

其中aj表示配电网节点位置, bj表示容量.DG安装的总容量必须满足约束条件.

从蜂群中随机选择一个初始群体, 对每个蜜蜂进行寻优, 将适应度最大的蜜蜂作为初始群体的发现者, 即找到该种群DG最佳安装节点和容量, 表达式为:

X={a|b}.

2.2人工蜂群算法

人工蜂群算法的基本步骤:

(1)首先通过随机条件选取一个初始群体P, 即包含Sn个初始解(蜜源数量).设第j个蜜源的位置Xj=(xj1,xj2,…,xjD)(j=1,2,…,Sn),其中D为优化参数的个数.

随机生成初始可行解的公式为

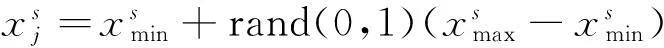
(1)

(2)雇佣蜂先在蜜源的某个区域进行一次搜索, 算出并与原位置蜜源的适应度值进行对比, 进行贪婪选择, 若新位置适应度值大于原位置, 则取代原位置的蜜源.

(3)雇佣蜂进行全部搜索后在固定的区域内以跳舞的形式将蜜源的信息传递给观察蜂, 观察蜂以轮赌盘的形式通过概率对雇佣蜂传递过来的信息重新选择蜜源.

(4)若某个蜜源经过多次搜索仍没有更新, 则与之对应的雇佣蜂放弃该处的蜜源, 并转换成一侦查蜂, 按照公式(1)在搜索空间探寻新蜜源位置替代原来的位置.

观察蜂对蜜源的位置进行选择的概率为:

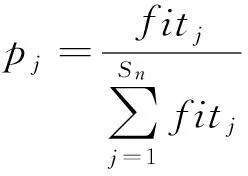
式中, fitj为第j个位置的蜜源所对应适应度大小.

式中, fj为第j个位置蜜源的目标函数值.

雇佣蜂和观察蜂对蜜源进行搜索的公式为:

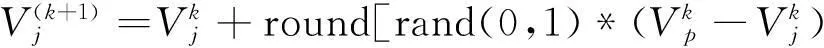
(2)

2.3改进的人工蜂群算法

由于人工蜂群算法存在比例适应度选择策略的缺点, 以至于错过潜在的较优个体, 这样不利于种群的多样性,并且其随机搜索速度不够快, 严重滞后了该算法进化速度.本文着重从下面两部分改进.

2.3.1均匀设计-反向寻优的初始化群体在ABC算法中, 随机选取一个初始群体, 若生成的初始群体不够合理, 会造成算法的全局寻优能力下降.本文对初始群体的选取进行改进, 使得初始个体分布均匀且质量比较优.文献[11]采用了反向学习的方法, 对群体进行初始化, 该方法对选取蜜源的质量有保证, 但是蜜源分布不均匀.文献[12]基于均匀设计的初始化策略, 保证了蜜源的均匀分布, 但是蜜源的质量不能保证.文中参考[12-13]优点, 采用均匀设计-反向学习的方法初始化群体.具体方法如下:

(1)将待初始化的群体均分成Sn个子空间, 从Sn个子空间中随机生成一个初始解, 按照公式(1)组合成初始个体.

(2)求出每个初始解的反向解, 公式为

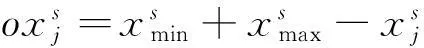
(3)在均化的蜜源上对初始个体与反向解个体进行排序, 选取最优的Sn个解组成初始蜜源集合.

2.3.2基于排序的选择策略在人工蜂群算法中, 适应度值决定了观察蜂选择该位置蜜源概率, 越大的适应度值, 观察蜂选择该位置的机率就大, 而较小适应度值的蜜源很有可能就会被观察蜂错过, 这样就会导致劣质蜜源上所包含的一些有用信息被错过.因此, 为了满足全局收敛性强和鲁棒性强的特点, 采用基于适应度排序的选择概率, 这种选择概率根据蜜源的适应度大小进行排序, 该位置的蜜源被选中的可能性仅仅是由其次序决定的, 其中第m位置的蜜源被选中的概率为:

(3)

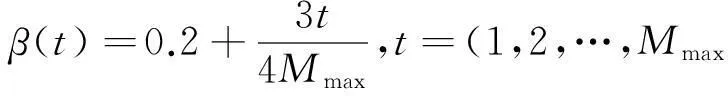
(4)

式中, β(t)表示蜜源的自适应参数, 为最大循环迭代次数.引入自适应参数机制, 在算法的进化初期, β(t)较小, 有利于搜寻到更多潜在可能最优的位置, 而在进化后期, 种群个体差异较小, 竞争力减弱, 可能造成算法停滞不前, 较大β(t)可以提高搜索速率, 有效地避免算法出现局部最优而停滞.

3　基于IABC算法的分布式电源选址与定容的实现

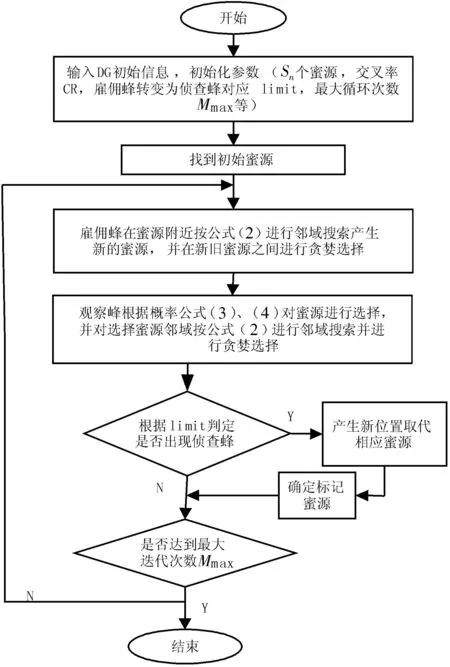
图1　基于IABC算法的流程图Fig.1　Flow chart of IABC

IABC算法流程见图1，具体步骤如下:

(1)输入配电网的原始数据, 获取系统节点和支路的信息.

(2)雇佣蜂在蜜源附近的有效区域内依据公式(2)对蜜源搜索, 并与原来蜜源进行贪婪选择观察蜂根据选择概率公式(3)和(4)对食物源进行选择, 并按照公式(2)搜索, 并在新旧蜜源之间进行贪婪选择.

(3)以limit为依据判定是否存在未被选择的蜜源, 如果存在, 放弃该位置, 此处的雇佣蜂转换为一侦查蜂, 重新搜索新位置的蜜源.

(4)首先记录当前的最优解, 根据最大迭代次数Mmax来判断最优解是否符合要求, 若当前的迭代次数达到Mmax, 计算停止, 将此时的最优解输出, 否则, 返回(2)循环执行命令.

4　算例分析

采用标准IEEE33节点配电测试系统作为算例来验证改进人工蜂群算法的有效性, 首先进行DG的布点规划, 如图2所示, 数字代表节点的编号.IEEE33节点网络是辐射状的配电网络, 该系统的额定电压为12.66 kV, 相角为0, 分布式电源接在1～32任意节点上[13], 总有功和无功功率分别是3 715.0 kW，2 300.0 kW.在该算法中, 设置参数为: 权重系数α=0.5,β=0.5,Sn取30, 交叉概率CR取0.5, limit取8,Mmax取60次, 有功功率的权重系数为w1=0.6；电压水平的权重系数为w2=0.4.运行算法程序.未接入DG时, 系统有功损耗是220.15 kW, 优化后系统的有功损耗是62.85 kW.

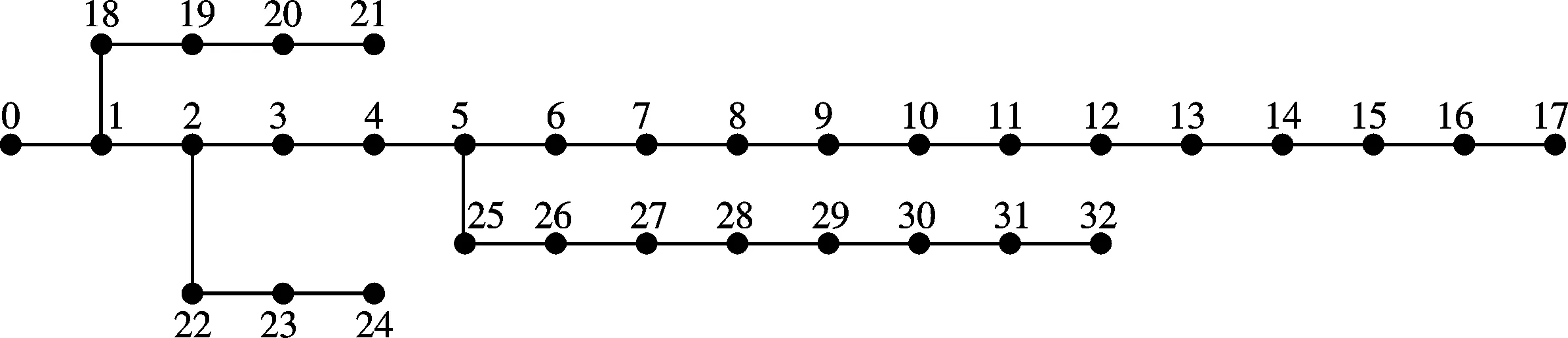
图2　IEEE 33系统Fig.2　IEEE33 system

两种算法在收敛性的比较如图3, 由图3可知, IABC算法较ABC算法在迭代次数以及收敛快慢上有着明显的提升.

表2为IABC和其他算法寻优结果.比较可得IABC算法中接入配电网中DG的总容量小于其余算法, 而且系统的网络损耗更小.因此IABC算法对于DG规划更加行之有效.

表2　不同优化方案结果比较

合理的规划DG的选址与定容, 也可以提高系统电压水平.在接入DG前后, 网络节点最低电压由0.913 1 p.u.上升到0.942 8 p.u.配电系统电压普遍有明显的改善.图4给出了系统节点电压比较.

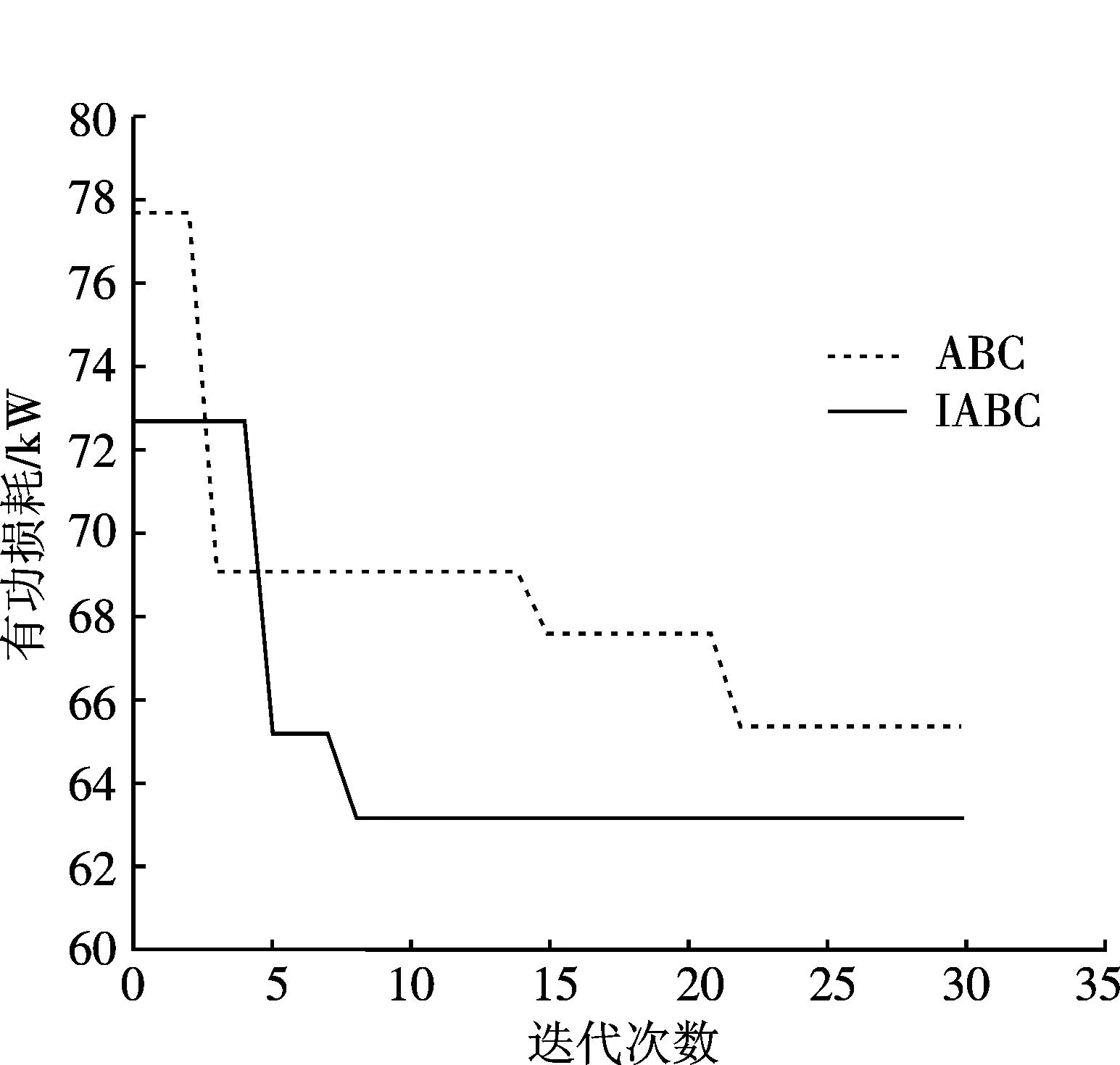
图3　两种算法在收敛性的比较Fig.3　Comparisons of ABC and IABC algorithm’s astringency

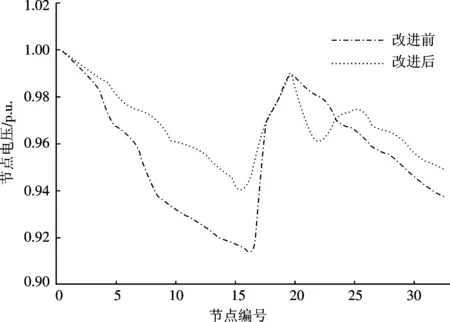
图4　33节点配电系统优化前后各节点电压水平分布Fig.4　Distribution of node voltage before and after 33-node distribution system optimization

5　结论

本文以降低配电网的网损及提高电压质量为优化目标, 为了避免陷入局部最优, 在标准人工蜂群算法的基础上, 运用均匀设计-反向寻优的方法来优化初始群体, 加快了全局寻优率.同时, 为了解决基于比例适应度选择不足的问题, 用基于适应度排序的选择概率代替了基于比例适应度的选择概率, 不仅使种群的多样性得到了保护, 而且扩大了全局搜索的范围.通过比较DG接入前后的配电网规划方案可以得出, DG的接入降低了网损, 改善了系统电压水平.

[1]刘健, 林涛, 李龙, 等. 分布式光伏接入情况下配电自动化系统的适应性[J]. 电力系统保护与控制, 2014,42(20):7-12.

[2]邱晓燕, 夏莉丽, 李兴源. 智能电网建设中分布式电源的规划[J]. 电网技术, 2010,34(4):7-10.

[3]李俊, 邓大上, 房鑫炎, 等. 考虑电压稳定裕度约束的点估计随机最优无功调度方法[J]. 电工技术学报, 2015,30(7):27-33.

[4]张建华, 曾博, 张玉莹, 等. 主动配电网规划关键问题与研究展望[J]. 电工技术学报, 2014,29(2):13-23.

[5]LANNOYE E, FLYNN D, O’MALLEY M. Evaluation of power system flexibility[J]. IEEE Trans Power Syst, 2012,27(2):922-931.

[6]胡殿刚, 张雪佼, 陈乃仕, 等. 新能源发电项目多维度后评价方法体系研究[J]. 电力系统保护与控制, 2015,43(4):10-17.

[7]张跃, 杨汾艳, 曾杰, 等. 主动配电网的分布式电源优化规划方案研究[J]. 电力系统保护与控制, 2014,43(15):67-72.

[8]KARABOGA D. An idea based on honey bee swarm for numerical optimization [R]. Kayseri: Engineering Faculty Computer Engineering Department, Bath University, 2005.

[9]胡泽春, 宋永华, 徐智威, 等. 电动汽车接入电网的影响与利用[J]. 中国电机工程学报, 2012,32(4):1-10,25.

[10]王振树, 卞绍润, 刘晓宇, 等. 基于混沌与量子粒子群算法相结合的负荷模型参数辨识研究[J]. 电工技术学报, 2014,29(12):211-217.

[11]North American Electric Reliability Corporation. Special report: potential reliability impacts of emerging flexible resources[R]. America: North American Electric Reliability Corporation (NERC), 2010:2-6.

[12]NIKNAM T. An efficient multi-objective HBMO algorithm for distribution feeder reconfiguration[J].Expert Syst Appl, 2011,38(3):2878-2887.

[13]KEHLER J H, HU M. Planning and operational considerations for power system flexibility[C] //Power and Energy Society General Meeting, Detroit, Michigan, IEEE, 2011:1-3.

(编辑CXM)

The Planning of Distributed Generation Based on Improved Artificial Bee Colony Algorithm

LOU Ning-na*, MAO Yi, HUANG Yuan-yu

(College of Electrical and Information Engineering, Hunan University, Changsha 410082, China)

In order to further optimize the sitting and sizing of distributed generation, a comprehensive optimization goal was proposed, which aims to minimize the transmission loss and maintain better voltage level, and determine the weight coefficient of different objectives using judgment matrix method. In order to improve the rate of global optimization, the uniform design and opposition-based optimizing were used. Meanwhile, in the improved algorithm, to overcome the shortage of selection based on the proportion of fitness, the selection based on fitness ranking probability is adopted instead of depending on the proportion of fitness, which not only protects the diversity of the population but also expands the global search range. Calculation results of standards IEEE 33-bus radial distribution system show that the proposed model is effective and reliable.

distributed power; artificial bee colony algorithm; rank fitness selection; uniform design; opposition-based optimizing

10.7612/j.issn.1000-2537.2016.03.010

2016-04-22基金项目：国家863计划资助项目(2012AA050215)*通讯作者,E-mail：1577699168@qq.com

TM714

A

1000-2537(2016)03-0056-06